多智能体系统（Agent-Based Model, ABM）和强化学习（Reinforcement Learning, RL）是两个不同但可结合的概念，尤其在复杂系统建模和人工智能领域有重要应用。下面分别解释它们，并说明二者的关联：

1. 多智能体系统（Agent-Based Model, ABM）

定义

ABM 是一种自底向上（简单规则能产生复杂秩序）的计算机模拟方法，通过定义大量自主交互的智能体（Agents（黄色字体） 及其行为规则，模拟复杂系统的宏观现象（如市场波动、流行病传播、生态系统演化等）。

a:“自底向上”（Bottom-Up）是一种方法论或设计思想，指从系统最基础的组成部分（底层）出发，通过定义其简单行为和交互规则，最终涌现（Emergence） 出复杂的整体现象。它与“自顶向下”（Top-Down）相对，后者是从宏观整体目标出发，逐层分解为子任务的设计方式

用ABM的例子理解“自底向上”

在多智能体系统（ABM） 中，“自底向上”体现为：

起点是微观个体：
先定义系统中每个智能体（Agent） 的属性和行为规则（例如：
- 个体属性：位置、能量值、年龄
- 行为规则：移动、觅食、躲避天敌、繁殖）。
关注局部交互：
智能体仅根据自身状态和邻近环境做决策（例如：
- “如果周围有食物，则靠近；如果发现捕食者，则逃跑”）。
宏观现象自然涌现：
所有智能体并行行动并持续交互后，系统会自发产生复杂的全局模式（例如：
- 鸟群在没有指挥的情况下形成编队飞行；
- 蚂蚁通过简单信息素规则构建出复杂的巢穴结构）。

✅ 核心思想：复杂系统无需中央控制，微观个体行为的叠加即可生成宏观秩序。

对比“自顶向下”（Top-Down）

维度	自底向上（Bottom-Up）	自顶向下（Top-Down）
起点	基础组件（如智能体、细胞）	整体目标（如系统功能、架构）
设计逻辑	组件行为 → 系统现象（涌现）	整体目标 → 分解为子任务 → 实现
控制方式	分布式、无中心控制	集中式、中央调控
典型应用	ABM、生物演化、群体智能	传统工程（如建楼、编写软件）

现实中的“自底向上”案例

蚂蚁觅食：
每只蚂蚁只遵循“释放信息素+跟随高浓度路径”的简单规则，最终整个蚁群找到食物源的最短路径。
金融市场波动：
每个交易者（智能体）根据个人策略买卖股票，无数交易行为的叠加导致股价涨跌（而非由中央机构直接设定价格）。
免疫系统：
免疫细胞独立识别并攻击病原体，整体形成免疫防御网络，无需“大脑”指挥。

为什么ABM必须用“自底向上”？

许多复杂系统（如社会、生态系统）的本质是去中心化的：

无法通过预设全局方程描述（例如无法用一个公式预测疫情传播的所有细节）；
微观个体的异质性和随机交互会导致“蝴蝶效应”。
ABM通过模拟底层个体行为，更真实地还原这类系统的动态演化。

总结：“自底向上” = 从局部个体出发 → 通过交互 → 生成全局复杂模式
它揭示了一个深刻原理：简单规则能产生复杂秩序（Simple rules create complex behaviors）。

智能体 = 虚拟世界中的独立个体（比如：游戏里的NPC、蚂蚁群中的单只蚂蚁、股市里的一个散户投资者），它能自己观察环境、做决策、和其他个体互动，最终影响整个系统。

1. 自主性（Autonomy）→ “有脑子，自己拿主意”

做什么：智能体不需要外部指挥，能根据自身目标独立做决策。

2. 交互性（Interaction）→ “会社交，能合作/竞争”

做什么：智能体之间能沟通、合作、竞争甚至欺骗。

3. 适应性（Adaptation）→ “吃一堑长一智”

做什么：智能体能根据经验调整行为（尤其在强化学习中）。

核心逻辑循环长这样：

while True:  # 持续自主运行1. 观察环境（收集周围信息）2. 分析自身状态（健康？疲劳？）3. 根据规则/学习策略做决策（移动？休息？）4. 执行动作（向前走一步）5. 与其他智能体互动（交换物资、传递消息）

特点	意味着什么	反例
自主	自己决定干什么	被遥控的玩具车
交互	会合作、竞争、沟通	孤岛上的鲁滨逊
有目标	努力达成任务（生存/赚钱等）	随波逐流的树叶
能适应	从经验中学习（高级智能体）	一成不变的时钟

核心特点

个体视角：每个智能体具有独立属性（位置、状态、策略等）和行为规则（移动、决策、交互）。
去中心化：宏观现象涌现自智能体间的局部交互，无需全局控制。
动态演化：系统随时间推进，智能体根据环境和其他智能体的行为调整策略。
应用场景：社会学、经济学、生物学、城市规划等复杂系统研究。

示例

模拟股市中投资者（智能体）的买卖行为如何引发市场波动。
预测疫情中个体接触如何影响传播速度。

2. 强化学习（Reinforcement Learning, RL）

定义

RL 是一种机器学习范式，智能体通过试错学习= 像生物进化一样实践出真知，在环境中采取行动以最大化累积奖励。核心是马尔可夫决策过程（MDP）。

试错学习在强化学习（RL）中如何运作？

假设训练一个机械狗学会走路的RL模型：

步骤	试错学习过程	对应RL术语
1. 尝试动作	机械狗随机向前迈腿	行动（Action）
2. 观察结果	摔倒/平稳站立/向前移动	状态（State）
3. 获得反馈	摔倒：扣分（惩罚）	奖励（Reward）
3. 获得反馈	移动：加分（奖励）	奖励（Reward）
4. 更新策略	减少导致摔倒的动作概率	策略优化（Policy Update）
4. 更新策略	增加能移动的动作概率	策略优化（Policy Update）
5. 重复循环	持续尝试新动作 → 积累经验 → 越走越好	学习收敛

马尔可夫决策过程（MDP）：马尔可夫决策过程（Markov Decision Process, MDP） 是强化学习（Reinforcement Learning）的核心数学框架，用于建模智能体（Agent）在环境中做序贯决策的问题。它的核心思想是：未来的状态只取决于当前状态和动作，与过去无关。

一、MDP的5大要素（用游戏《超级马里奥》类比）

MDP要素	定义	游戏中的例子
状态（State）	环境的当前情况	当前画面信息：马里奥位置、敌人位置、金币数等
动作（Action）	智能体能做的行为	按手柄键：← → ↑ ↓（左移/右移/跳跃/蹲下）
奖励（Reward）	动作的即时反馈（数值）	吃金币+1分，踩死敌人+2分，掉进坑里-10分（游戏结束）
状态转移（Transition）	动作如何改变环境状态	按→键后，马里奥向右移动一格（可能触发敌人靠近）
折扣因子（γ）	衡量未来奖励的重要性（0≤γ<1）	γ=0.9：未来1步的奖励折算为90%，未来10步只剩35%

二、现实中的MDP应用

场景	状态（State）	动作（Action）	奖励（Reward）
自动驾驶	车辆位置、周边障碍物	转向/加速/刹车	安全抵达+100，碰撞-100，平稳行驶+0.1/秒
推荐系统	用户历史点击+当前页面	推送商品A/B/C	点击+1，购买+10，忽略-0.1
机器人抓取	机械臂角度+目标物体位置	关节转动方向/力度	抓取成功+50，掉落-20，耗时-0.01/秒

MDP = 环境的状态转移 + 智能体的决策目标

三、与非马尔可夫过程的区别

若状态不能完全描述环境历史信息，则MDP失效 → 需升级为：

部分可观测MDP（POMDP）：如打牌时看不到对手手牌。
循环神经网络（RNN）：用记忆单元存储历史信息（如语言翻译）。

核心要素
智能体（Agent）：学习者与决策者。
环境（Environment）：智能体交互的外部系统。
状态（State）：环境的当前情况。
动作（Action）：智能体的行为选择。
奖励（Reward）：环境对动作的即时反馈。
目标：学习最优策略（Policy）以最大化长期奖励。
学习机制

智能体通过探索（尝试新动作）和利用（选择已知高奖励动作）来优化策略，常用算法包括：
Q-Learning、DQN（深度Q网络）
策略梯度（Policy Gradient）
Actor-Critic 方法
应用场景

游戏AI（AlphaGo）、机器人控制、自动驾驶等。

3. ABM 与 RL 的结合：多智能体强化学习（MARL）

当ABM中的智能体具备学习能力时，可引入强化学习，形成多智能体强化学习（Multi-Agent RL, MARL）。这是当前AI研究的热点。

关键挑战

环境非平稳性：多个智能体同时学习导致环境动态变化。
信用分配：如何将系统级奖励公平分配给个体？
合作与竞争：智能体目标可能冲突（竞争）或一致（合作）。

解决方法

集中式训练+分布式执行：训练时共享信息，执行时独立行动（如MADDPG）。
通信机制：智能体学习沟通协议以协作（如CommNet）。
博弈论框架：用纳什均衡等概念建模智能体交互（如Fictitious Play）。

应用场景

自动驾驶车队协同优化路线。
多机器人协作搬运物体。
电力市场中多个发电商的动态竞价策略。

4. 对比总结

维度	多智能体系统（ABM）	强化学习（RL）	结合（MARL）
核心目标	模拟复杂系统涌现现象	学习最大化累积奖励的策略	智能体在交互中学习协作/竞争策略
智能体行为	预定义规则或简单启发式	通过试错优化策略	自适应学习策略
系统动态	由局部交互驱动	由奖励函数驱动	学习与交互共同驱动
典型应用	社会模拟、流行病传播	游戏AI、机器人控制	多机器人系统、智能交通

5. 通俗理解

ABM 像模拟一群鸟的飞行：每只鸟按简单规则（避免碰撞、跟随邻居）行动，整体形成鸟群。
RL 像训练一只狗：做对动作给奖励，最终学会指令。
MARL 则是训练一群协作的狗：每只狗需学习如何与其他狗配合完成任务（如共同拉雪橇）。

二者结合为研究智能群体行为提供了强大工具，尤其在去中心化决策、分布式AI系统中前景广阔。

本项目基于2015年全国大学生数学建模竞赛B题，使用多智能体系统(Agent-Based Model)和强化学习方法来研究出租车资源配置问题。通过创新的建模方法，实现了对城市出租车供求关系的动态分析和优化。

通过对题目的理解与分析，可以知道问题背景:

随着“互联网+”时代的到来，多家公司依托移动互联网建立了打车软件服务平台，实现了乘客与出租车司机之间的信息互通。为了缓解“打车难”问题，各平台推出了多种出租车补贴方案。然而，这些方案可能存在不足，需要设计新的补贴方案以改善现状。

可以提取到的要点有：

1.供求匹配程度分析：需要量化不同时空下出租车供给与乘客需求之间的匹配情况。

2.补贴方案影响评估：评估现有补贴方案对缓解打车难问题的效果。

3.新补贴方案设计：设计新的补贴方案，并通过模型验证其合理性。（多智能体系统（MAS）和强化学习方法可以构成第三问中设计新打车软件服务平台补贴方案的一种可行模型框架。）

分析方法

数据收集：收集出租车轨迹数据、乘客打车请求数据、补贴方案数据等。
供求匹配指标：定义如“打车成功率”、“平均等待时间”等指标来量化供求匹配程度。
补贴方案建模：将补贴方案建模为影响出租车司机和乘客行为的因素，分析其对供求关系的影响。
强化学习优化：使用强化学习来优化补贴策略，以最大化某种长期奖励（如乘客满意度、出租车利用率）。

怎么去理解第一题：

问题本质、现有方案逻辑、核心矛盾、数据支撑四个维度展开：

一、理解题目：明确问题本质与目标

题目定位
第一题通常要求分析现有补贴方案的设计逻辑、实施效果及存在的问题，为后续设计新方案提供对比基准。
2.核心目标

二、解决步骤：系统性分析现有方案
- 示例题目：
  “分析当前主流打车软件（如滴滴、Uber）的乘客与司机补贴策略，指出其设计缺陷及对出租车资源配置效率的影响。”
  - 识别现有方案的目标用户、激励手段、成本结构。
  - 量化分析补贴对供需匹配、市场效率、用户行为的影响。
  - 提炼关键矛盾（如“补贴导致司机挑单”“高峰时段供需失衡加剧”）。
步骤1：拆解现有补贴方案类型

按补贴对象和场景分类，典型方案包括：
- 乘客端补贴：
  - 起步价折扣（如首单立减5元）
  - 动态折扣（根据供需比调整，如非高峰时段8折）
  - 忠诚度奖励（如连续打车3次返现10元）
- 司机端补贴：
  - 高峰时段溢价（如早晚高峰每单额外补贴2元）
  - 长距离订单补贴（如订单超过10公里后每公里补贴0.5元）
  - 空驶补偿（如司机在特定区域等待超过10分钟未接单，补偿5元）
- 综合补贴：
  - 平台促销活动（如“周末打车全城5折”）
  - 节假日专项补贴（如春节期间司机接单奖励翻倍）
步骤2：分析补贴方案的设计逻辑与目标**
- 乘客端逻辑：
  - 目标：降低打车门槛，吸引新用户，提高非高峰时段需求。
  - 手段：通过价格敏感度测试（如A/B测试）确定最优折扣力度。
- 司机端逻辑：
  - 目标：激励司机在供需紧张时段/区域出车，减少空驶。
  - 手段：基于历史数据预测高峰时段，动态调整补贴系数。
- 平台端逻辑：
  - 目标：平衡供需以提升匹配率，同时控制补贴成本占比（如不超过订单金额的15%）。
步骤3：量化评估补贴方案的实施效果**

通过数据指标验证方案有效性：
- 乘客端效果：
  - 补贴后订单量变化（如起步价折扣使订单量提升20%）
  - 用户留存率（如忠诚度奖励使月活用户增加15%）
- 司机端效果：
  - 高峰时段接单率（如溢价补贴使接单率从60%提升至85%）
  - 空驶率变化（如空驶补偿使空驶时间减少30%）
- 市场效率效果：
  - 供需匹配率（如动态折扣使匹配率从70%提升至85%）
  - 乘客平均等待时间（如补贴优化后等待时间缩短至5分钟内）
步骤4：识别现有方案的核心矛盾与缺陷**

结合数据与用户反馈，提炼关键问题：
- 补贴依赖性：
  - 乘客对低价敏感，补贴停止后订单量骤降（如某平台取消起步价折扣后，次日订单量下降40%）。
  - 司机为追求补贴频繁切换平台，导致服务碎片化。
- 供需错配：
  - 静态补贴无法适应实时供需变化（如固定高峰补贴导致非核心区域司机过剩）。
- 成本不可控：
  - 过度补贴侵蚀平台利润（如某季度补贴成本占营收的25%，导致亏损）。
- 公平性争议：
  - 司机因补贴差异产生收入分化（如长距离订单补贴使长途司机收入高于短途司机30%）。
- 行为扭曲：
  - 乘客滥用补贴（如通过虚拟定位获取多地优惠），司机挑单（如只接高补贴订单）。
三、案例分析：以滴滴出行补贴方案为例

1. 现有方案描述
- 乘客端：
  - 起步价折扣（新用户首单立减10元）
  - 动态折扣（非高峰时段8折，高峰时段9折）
  - 周末全城打车券（满30减5元）
- 司机端：
  - 早晚高峰溢价（7:00-9:00、17:00-19:00每单补贴2元）
  - 远途补贴（订单超过15公里后，每公里补贴0.8元）
  - 空驶补偿（司机在机场等待超过20分钟未接单，补偿10元）
2. 效果评估
- 乘客端：
  - 新用户首单立减使日新增用户提升35%，但次月留存率仅18%（低于行业平均25%）。
  - 动态折扣使非高峰时段订单量增加22%，但高峰时段因折扣力度不足，供需匹配率仅68%。
- 司机端：
  - 高峰溢价使接单率从65%提升至82%，但司机集中涌入核心区域，导致郊区供需失衡（匹配率不足50%）。
  - 远途补贴使长途订单占比从15%提升至25%，但司机因长途疲劳产生投诉率上升10%。
- 平台端：
  - 补贴成本占营收的18%，导致季度净利润下降5个百分点。
3. 核心矛盾
- 短期激励与长期粘性冲突：低价补贴吸引用户，但未建立服务差异化，导致用户忠诚度低。
- 静态规则与动态市场矛盾：固定补贴时段/区域无法适应突发供需变化（如演唱会散场时的短时需求激增）。
- 成本效率失衡：过度补贴司机端导致平台利润压缩，而乘客端补贴效果边际递减。
四、解决思路：针对缺陷提出改进方向
- 动态化补贴设计：
  - 引入实时供需比（如每10分钟更新一次补贴系数），在突发需求时自动提高补贴力度。
- 差异化补贴策略：
  - 根据用户画像（如高频用户、企业客户）设计分层补贴，避免“一刀切”导致的资源浪费。
- 成本可控机制：
  - 设置补贴预算上限，采用“补贴池”动态分配（如高峰时段优先消耗预算，非高峰时段保留余量）。
- 行为约束规则：
  - 对滥用补贴的用户/司机设置惩罚（如虚假定位3次后暂停优惠资格，挑单司机降低接单优先级）。
- 多目标优化模型：
  - 构建多智能体强化学习模型，平衡匹配率、空驶率、成本、公平性等多维度目标。

五、总结：回答第一题的关键要点

结构化呈现：
- 按“方案类型→设计逻辑→效果评估→核心矛盾”的逻辑展开。
数据支撑：
- 引用具体指标（如订单量、匹配率、成本占比）增强说服力。
问题聚焦：
- 避免泛泛而谈，紧扣“资源配置效率”这一核心矛盾（如供需错配、成本浪费）。
改进导向：
- 在分析缺陷时，隐含后续设计新方案的思路（如动态化、差异化）。

三、案例分析：以滴滴出行补贴方案为例

1. 现有方案描述

乘客端：
- 起步价折扣（新用户首单立减10元）
- 动态折扣（非高峰时段8折，高峰时段9折）
- 周末全城打车券（满30减5元）
司机端：
- 早晚高峰溢价（7:00-9:00、17:00-19:00每单补贴2元）
- 远途补贴（订单超过15公里后，每公里补贴0.8元）
- 空驶补偿（司机在机场等待超过20分钟未接单，补偿10元）

2. 效果评估

乘客端：
- 新用户首单立减使日新增用户提升35%，但次月留存率仅18%（低于行业平均25%）。
- 动态折扣使非高峰时段订单量增加22%，但高峰时段因折扣力度不足，供需匹配率仅68%。
司机端：
- 高峰溢价使接单率从65%提升至82%，但司机集中涌入核心区域，导致郊区供需失衡（匹配率不足50%）。
- 远途补贴使长途订单占比从15%提升至25%，但司机因长途疲劳产生投诉率上升10%。
平台端：
- 补贴成本占营收的18%，导致季度净利润下降5个百分点。

3. 核心矛盾

短期激励与长期粘性冲突：低价补贴吸引用户，但未建立服务差异化，导致用户忠诚度低。
静态规则与动态市场矛盾：固定补贴时段/区域无法适应突发供需变化（如演唱会散场时的短时需求激增）。
成本效率失衡：过度补贴司机端导致平台利润压缩，而乘客端补贴效果边际递减。

四、解决思路：针对缺陷提出改进方向

动态化补贴设计：
- 引入实时供需比（如每10分钟更新一次补贴系数），在突发需求时自动提高补贴力度。
差异化补贴策略：
- 根据用户画像（如高频用户、企业客户）设计分层补贴，避免“一刀切”导致的资源浪费。
成本可控机制：
- 设置补贴预算上限，采用“补贴池”动态分配（如高峰时段优先消耗预算，非高峰时段保留余量）。
行为约束规则：
- 对滥用补贴的用户/司机设置惩罚（如虚假定位3次后暂停优惠资格，挑单司机降低接单优先级）。
多目标优化模型：
- 构建多智能体强化学习模型，平衡匹配率、空驶率、成本、公平性等多维度目标（参考前文MAS-RL框架）。

五、总结：回答第一题的关键要点

结构化呈现：
- 按“方案类型→设计逻辑→效果评估→核心矛盾”的逻辑展开。
数据支撑：
- 引用具体指标（如订单量、匹配率、成本占比）增强说服力。
问题聚焦：
- 避免泛泛而谈，紧扣“资源配置效率”这一核心矛盾（如供需错配、成本浪费）。
改进导向：
- 在分析缺陷时，隐含后续设计新方案的思路（如动态化、差异化）。

示例回答框架：

“当前打车软件补贴方案以静态折扣和固定时段溢价为主，虽在短期内提升了订单量（如乘客起步价折扣使日订单增长20%），但存在三大缺陷：

供需错配：固定高峰补贴导致司机集中涌入核心区域，郊区匹配率不足50%；
成本失控：补贴成本占营收的18%，压缩平台利润空间；
行为扭曲：司机挑单现象频发（高补贴订单接单率比普通订单高40%）。
后续需设计动态化、差异化的补贴机制，以优化资源配置效率。”

第二题”（通常指出租车资源配置问题中的补贴方案评估或优化部分），需从问题背景、分析目标、数学建模、MATLAB实现逻辑四个层面逐步拆解。

一、问题背景与核心目标

1. 现实场景

打车难问题：高峰期（如早晚高峰）乘客需求激增，但出租车供给不足，导致匹配率低、等待时间长。
补贴的作用：通过经济激励（如高峰期额外补贴）鼓励司机在需求高的区域或时间段接单，从而平衡供求。

2. 核心目标

评估现有补贴方案：量化不同补贴策略（如无补贴、高峰期补贴、全天补贴）对匹配率、等待时间的影响。
优化补贴策略：通过强化学习找到动态补贴方案，使系统整体匹配率最大化或等待时间最小化。

二、数学建模：如何量化补贴效果？

1. 关键变量定义

变量	含义	示例值
Dt	t时刻的乘客需求量（订单数）	早高峰8:00-9:00：1500单
St	t时刻的出租车供给量（空闲车数）	早高峰：800辆
Mt	t时刻的匹配率（成功打车比例）	Mt=min(St/Dt,1)
Rt	t时刻的补贴金额（元）	早高峰补贴10元，其他时段0元
α	补贴对供给的弹性系数	假设补贴10元使供给增加10%

2. 补贴效果模型

3. 强化学习优化框架

状态（State）：当前时间 t、当前需求 Dt、当前供给 St。
动作（Action）：选择补贴方案（如无补贴、补贴5元、补贴10元）。
奖励（Reward）：匹配率提升量或等待时间减少量：

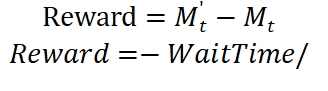
目标：通过Q-learning或深度强化学习（DQN）学习最优补贴策略 π∗(t)，使长期累积奖励最大化。

在“互联网+”时代的出租车资源配置问题中，第三题通常要求设计一个新的打车软件服务平台补贴方案，并论证其合理性。

分析现有补贴方案的不足：
- 收集并分析现有打车软件服务平台的补贴方案，如乘客返现补贴、出租车高峰加价补贴、司机短途订单补贴等。
- 识别这些方案在缓解“打车难”问题上的局限性，如补贴力度不足、补贴范围有限、补贴方式不合理等。
设计新的补贴方案：
- 乘客补贴：考虑乘客的出行需求、支付能力等因素，设计合理的乘客补贴政策。例如，可以根据乘客的打车频次、出行距离等因素给予不同程度的补贴，以提高乘客使用打车软件的积极性。
- 司机补贴：结合司机的运营成本、收入水平等因素，设计合理的司机补贴政策。例如，可以根据司机的接单数、行驶里程、空驶率等因素给予补贴，以提高司机出车载客的积极性。
- 动态调整机制：建立补贴方案的动态调整机制，根据实时供需情况、交通状况等因素动态调整补贴力度和范围，以确保补贴方案的有效性和灵活性。
论证补贴方案的合理性：
- 数学建模：构建多目标规划模型、层次分析模型等数学模型，以量化分析补贴方案对缓解“打车难”问题的效果。例如，可以通过模型计算补贴方案实施前后的匹配率、等待时间、空驶率等指标的变化情况。
- 数据分析：收集并分析实际数据，如打车订单数据、乘客和司机的反馈数据等，以验证补贴方案的实际效果。例如，可以通过对比分析补贴方案实施前后的订单量、乘客满意度等指标来评估补贴方案的有效性。
- 案例研究：参考其他城市或地区的成功案例，分析其补贴方案的设计思路和实施效果，为自身补贴方案的设计提供借鉴和参考。

问题重述

一、问题背景

随着“互联网+”技术的快速发展，打车软件服务平台应运而生，实现了乘客与出租车司机之间的信息高效互通，有效缓解了传统打车方式中的信息不对称问题。然而，在高峰时段或特定区域，仍存在“打车难”的现象，表现为乘客等待时间长、司机空驶率高、出租车资源配置效率低下等。为了进一步优化出租车资源配置，提高市场效率，各打车软件服务平台纷纷推出了多种补贴方案，但这些方案在实施过程中仍存在诸多不足。

二、现有补贴方案分析

乘客补贴方案：
- 形式：如乘客返现补贴、优惠券发放等。
- 不足：补贴力度可能不足，无法显著降低乘客的打车成本；补贴范围有限，可能仅针对特定用户或特定时段；补贴方式单一，缺乏灵活性。
司机补贴方案：
- 形式：如出租车高峰加价补贴、司机短途订单补贴等。
- 不足：补贴可能未能充分激励司机在高峰时段或供需紧张的区域出车；补贴计算方式可能复杂，导致司机理解困难；补贴发放可能不及时，影响司机积极性。
综合补贴方案：
- 形式：结合乘客和司机补贴的综合性方案。
- 不足：可能未能精准匹配供需关系，导致资源错配；方案调整可能滞后，无法适应市场动态变化。

三、问题目标

基于上述背景和分析，本问题的目标在于：

设计新的打车软件服务平台补贴方案：
- 综合考虑乘客和司机的利益，设计一套既能够降低乘客打车成本、提高乘客使用打车软件积极性，又能够激励司机在高峰时段或供需紧张区域出车、降低空驶率的补贴方案。
论证新补贴方案的合理性：
- 通过数学建模、数据分析等方法，论证新补贴方案在缓解“打车难”问题、提高出租车资源配置效率方面的有效性。
- 确保新补贴方案在经济效益上具有可行性，即平台能够承担补贴成本，同时实现可持续发展。

四、新补贴方案设计方向

乘客补贴设计：
- 起步补贴：乘客每次打车起步时给予一定金额的补贴，降低打车门槛。
- 动态折扣：根据实时供需情况，为乘客提供动态折扣，鼓励乘客在非高峰时段或供需平衡区域打车。
- 忠诚度奖励：对频繁使用打车软件的乘客给予额外奖励，提高用户粘性。
司机补贴设计：
- 高峰时段补贴：在高峰时段给予司机额外的补贴，鼓励司机出车接客。
- 长距离订单补贴：对长距离订单给予司机更高的补贴，弥补司机因长途行驶而增加的成本。
- 空驶补偿：当司机在特定区域内空驶一定时间后，给予一定的空驶补偿，降低司机空驶成本。
动态调整机制：
- 建立补贴方案的动态调整机制，根据实时供需情况、交通状况、天气因素等动态调整补贴力度和范围。
- 利用大数据和人工智能技术，对补贴方案进行实时优化和调整，确保方案的有效性和灵活性。

五、预期成果

提交一份详细的问题分析报告：
- 包括问题背景、现有补贴方案分析、问题目标、新补贴方案设计方向等内容。
构建数学模型并进行分析：
- 利用多目标规划模型、层次分析模型等数学模型，对新补贴方案进行量化分析和论证。
提出具体的新补贴方案：
- 包括乘客补贴和司机补贴的具体设计、动态调整机制的实施细节等。
验证新补贴方案的有效性：
- 通过案例分析、模拟实验或实际数据验证等方法，验证新补贴方案在缓解“打车难”问题、提高出租车资源配置效率方面的有效性。

分析步骤与MATLAB实现

步骤1：数据预处理

目标：清洗数据，提取有效信息（如按小时/区域统计供求）。

% 示例：生成模拟数据（实际需替换为真实数据）
hours = 1:24; % 一天24小时
num_taxis = 1000; % 出租车数量
num_requests = randi([500, 2000], 1, 24); % 每小时随机请求数% 模拟出租车供给（高峰期供给减少）
supply = num_taxis * (0.8 + 0.4*sin((hours-10)*pi/12)); % 正弦波动模拟早晚高峰% 存储为表格
data = table(hours', supply', num_requests', 'VariableNames', {'Hour', 'Supply', 'Demand'});

步骤2：供求匹配分析

目标：计算打车成功率和平均等待时间。

% 打车成功率 = 供给 / 需求（简化模型，实际需考虑动态匹配）
match_rate = min(data.Supply ./ data.Demand, 1); % 避免>100%% 模拟等待时间（需求越高，等待时间越长）
wait_time = 5 ./ (1 + exp(-0.5*(data.Demand - 1000))); % Logistic函数模拟% 绘制匹配率曲线
figure;
plot(data.Hour, match_rate, '-o', 'LineWidth', 2);
xlabel('小时');
ylabel('打车成功率');
title('供求匹配率随时间变化');
grid on;

步骤3：补贴方案评估

目标：比较不同补贴策略对匹配率的影响。

% 定义三种补贴方案（示例：高峰期补贴金额）
subsidy_schemes = {'无补贴', '高峰期补贴10元', '全天补贴5元'};
subsidy_effects = [0, 0.1, 0.05]; % 假设补贴提升匹配率的系数% 计算补贴后的匹配率
matched_rates = match_rate .* (1 + subsidy_effects'); % 列向量转置相乘% 绘制对比柱状图
figure;
bar(matched_rates);
set(gca, 'XTickLabel', hours, 'XTick', 1:24);
xticks(1:6:24); % 每6小时显示一个标签
xlabel('小时');
ylabel('补贴后匹配率');
title('不同补贴方案效果对比');
legend(subsidy_schemes, 'Location', 'southeast');
grid on;

步骤4：强化学习优化补贴（简化版）

目标：用Q-learning找到最优补贴策略（此处简化状态和动作空间）。

% 定义状态（当前小时）和动作（补贴方案索引）
num_states = 24; % 24小时
num_actions = length(subsidy_schemes);
Q = zeros(num_states, num_actions); % 初始化Q表% 强化学习参数
alpha = 0.1; % 学习率
gamma = 0.9; % 折扣因子
epsilon = 0.1; % 探索率
episodes = 100; % 训练轮数% 简化奖励函数：匹配率提升越大，奖励越高
for episode = 1:episodesstate = randi(num_states); % 随机初始状态while true% ε-贪婪策略选择动作if rand < epsilonaction = randi(num_actions);else[~, action] = max(Q(state, :));end% 执行动作，获取奖励（简化：直接用补贴效果作为奖励）reward = subsidy_effects(action);% 假设下一状态随机（实际需根据动态模型更新）next_state = mod(state, num_states) + 1;% Q表更新Q(state, action) = Q(state, action) + alpha * (reward + gamma * max(Q(next_state, :)) - Q(state, action));% 终止条件（此处简化，实际需定义）if rand < 0.01break;endstate = next_state;end
end% 提取最优策略
[~, optimal_policy] = max(Q, [], 2);
optimal_subsidy = subsidy_schemes(optimal_policy);
disp('最优补贴策略（每小时）：');
disp(optimal_subsidy');

三、完整代码与图表生成

完整MATLAB脚本zhe

%% 1. 数据生成与预处理
hours = 1:24;
num_taxis = 1000;
num_requests = randi([500, 2000], 1, 24);
supply = num_taxis * (0.8 + 0.4*sin((hours-10)*pi/12));
data = table(hours', supply', num_requests', 'VariableNames', {'Hour', 'Supply', 'Demand'});%% 2. 供求匹配分析
match_rate = min(data.Supply ./ data.Demand, 1);
wait_time = 5 ./ (1 + exp(-0.5*(data.Demand - 1000)));figure;
subplot(2,1,1);
plot(data.Hour, match_rate, '-o', 'LineWidth', 2);
title('打车成功率随时间变化');
grid on;subplot(2,1,2);
plot(data.Hour, wait_time, '-r', 'LineWidth', 2);
title('平均等待时间随时间变化');
grid on;%% 3. 补贴方案评估
subsidy_schemes = {'无补贴', '高峰期补贴10元', '全天补贴5元'};
subsidy_effects = [0, 0.1, 0.05];
matched_rates = match_rate .* (1 + subsidy_effects');figure;
bar(matched_rates);
set(gca, 'XTickLabel', hours, 'XTick', 1:24);
xticks(1:6:24);
xlabel('小时');
ylabel('补贴后匹配率');
title('不同补贴方案效果对比');
legend(subsidy_schemes, 'Location', 'southeast');
grid on;%% 4. 强化学习优化（简化版）
num_states = 24;
num_actions = length(subsidy_schemes);
Q = zeros(num_states, num_actions);
alpha = 0.1; gamma = 0.9; epsilon = 0.1; episodes = 100;for episode = 1:episodesstate = randi(num_states);while trueif rand < epsilonaction = randi(num_actions);else[~, action] = max(Q(state, :));endreward = subsidy_effects(action);next_state = mod(state, num_states) + 1;Q(state, action) = Q(state, action) + alpha * (reward + gamma * max(Q(next_state, :)) - Q(state, action));if rand < 0.01break;endstate = next_state;end
end[~, optimal_policy] = max(Q, [], 2);
optimal_subsidy = subsidy_schemes(optimal_policy);
disp('最优补贴策略（每小时）：');
disp(optimal_subsidy');

这道题呢，没有给出相关数据，我们这些数据要怎么来呢?

一、真实数据来源（需授权）

1. 交通传感器网络

设备类型：地磁传感器、雷达、摄像头、线圈检测器等。
数据格式：通常为时间序列，每5-15分钟记录一次流量（车辆数/小时）。
获取方式：
- 联系当地交通管理部门（如市政厅、交通局）申请开放数据接口。
- 使用公开数据集（如CalTrans PeMS、HighD Dataset）。

2. 第三方API

示例：
- 高德地图/百度地图API：通过调用交通态势接口获取实时流量。
- TomTom Traffic API：提供历史和实时交通数据。
MATLAB调用示例（需替换为实际API密钥）：

% 伪代码：调用高德地图API获取流量（需安装Web访问工具箱）
url = 'https://restapi.amap.com/v3/traffic/status/road?key=YOUR_KEY&name=北京路';
data = webread(url);
trafficFlow = str2double(data.trafficinfo.status); % 解析JSON响应

3. 开源数据集

推荐数据集：
- Metr-La（洛杉矶高速公路流量）：包含207个传感器、34,272个时间戳。
- PEMS-BAY（湾区交通数据）：325个传感器、52,116个时间戳。
加载方式（需提前下载数据文件）：

% 加载PEMS数据（示例为CSV格式）
data = readmatrix('pems_bay.csv'); % 行为传感器，列为时间
trafficFlow = data(:, 1:24); % 取前24小时数据

二、模拟数据生成（无需外部依赖）

当无法获取真实数据时，可通过数学模型生成符合交通规律的模拟数据。以下是3种常用方法及MATLAB实现：

方法1：正弦波+随机噪声（周期性流量）

适用于模拟早晚高峰的规律性波动：

% 参数设置
numRegions = 10;       % 区域数量
hours = 24;            % 时间范围（小时）
baseFlow = 5;          % 基础流量
amplitude = 8;         % 波动幅度
noiseLevel = 2;        % 随机噪声强度% 生成数据
time = (1:hours)';
trafficFlow = baseFlow + amplitude * sin(time/4) + noiseLevel * randn(hours, numRegions)';% 可视化检查
figure;
plot(time, trafficFlow);
xlabel('时间（小时）'); ylabel('流量');
title('模拟周期性交通流量');

方法2：基于泊松过程的随机事件模型

模拟突发事故或信号灯变化导致的流量突变：

% 参数设置
lambda = 0.1;          % 事件发生率（每小时）
numEvents = poissrnd(lambda * hours); % 总事件数
eventTimes = sort(rand(numEvents, 1) * hours); % 事件发生时间% 初始化流量矩阵
trafficFlow = zeros(hours, numRegions);
for t = 1:hours% 基础流量base = 5 + 3 * randn();% 应用事件影响（如事故导致流量骤降）for e = 1:numEventsif eventTimes(e) >= t-0.5 && eventTimes(e) < tbase = max(1, base - 10); % 流量减少10endendtrafficFlow(t, :) = base + 2 * randn(1, numRegions);
end% 可视化
figure;
plot(1:hours, trafficFlow);
title('基于事件模型的交通流量');

方法3：多区域空间关联模型

模拟相邻区域流量的相关性（如主干道与支路）：

% 参数设置
numRegions = 5;
hours = 24;
corrMatrix = [1, 0.8, 0.3, 0.1, 0;  % 区域相关性矩阵0.8, 1, 0.5, 0.2, 0;0.3, 0.5, 1, 0.6, 0.1;0.1, 0.2, 0.6, 1, 0.4;0, 0, 0.1, 0.4, 1];% 生成相关随机数
mu = 5 * ones(1, numRegions);
sigma = 2 * ones(1, numRegions);
X = mvnrnd(mu, diag(sigma) * corrMatrix * diag(sigma), hours);% 添加时间趋势
time = (1:hours)';
trafficFlow = X + 2 * sin(time/6)' .* (1:numRegions);% 可视化
figure;
imagesc(trafficFlow);
colorbar;
title('多区域空间关联流量热力图');

三、数据验证与预处理

无论数据来源如何，均需进行以下检查：

缺失值处理：

% 用线性插值填充缺失值
trafficFlow = fillmissing(trafficFlow, 'linear');

2.异常值修正：

% 剔除超过3倍标准差的值
threshold = 3 * std(trafficFlow(:));
trafficFlow(abs(trafficFlow) > threshold) = NaN;
trafficFlow = fillmissing(trafficFlow, 'nearest');

3.归一化（可选）：

% 缩放到[0,1]范围
trafficFlow = (trafficFlow - min(trafficFlow(:))) / range(trafficFlow(:));

四、完整示例：从模拟到可视化

以下代码整合了模拟数据生成和3D曲面动画：

% 生成模拟数据
numRegions = 8;
hours = 24;
[region, time] = meshgrid(1:numRegions, 1:hours);
trafficFlow = 10 + 5*sin(time/4) + 3*randn(size(time));% 创建视频
videoFile = 'traffic_simulation.mp4';
writerObj = VideoWriter(videoFile, 'MPEG-4');
open(writerObj);figure('Color', 'white');
for t = 1:hours% 更新曲面数据surf(region, time(:,1:t), trafficFlow(:,1:t), 'EdgeColor', 'none');colormap(jet); colorbar;zlim([0 20]);xlabel('区域'); ylabel('时间'); zlabel('流量');title(sprintf('交通流量动态模拟（时间=%d:00）', t-1));% 添加当前时间标记hold on;plot3(region(1,:), t*ones(1,numRegions), trafficFlow(t,:), 'r-', 'LineWidth', 2);hold off;frame = getframe(gcf);writeVideo(writerObj, frame);
end
close(writerObj);

总结

数据来源	优点	缺点	适用场景
真实传感器	数据准确，反映实际规律	获取成本高，需授权	学术研究、商业项目
第三方API	实时性强，更新频繁	可能收费，速率限制	实时监控系统
开源数据集	免费，结构规范	地域/时间范围有限	算法验证、基准测试
模拟数据	完全可控，无需外部依赖	与真实场景存在偏差	原型开发、教学演示

完整代码：交通流量分析与可视化

%% 1. 数据生成（模拟多区域交通流量）
clc; clear; close all;
rng(42); % 固定随机种子保证可重复性% 参数设置
numRegions = 5;      % 区域数量
hours = 24*7;        % 模拟7天（每小时一个数据点）
baseFlow = linspace(10, 50, numRegions)'; % 基础流量（区域差异）% 生成数据：基础流量 + 时间效应 + 噪声
timeIdx = 1:hours;
timeEffect = 20 * sin(timeIdx/4)'; % 周期性波动（如早晚高峰）
noise = 5 * randn(hours, numRegions); % 随机噪声% 最终流量数据（时间×区域）
trafficFlow = repmat(baseFlow, 1, hours)' + timeEffect + noise;
trafficFlow = max(trafficFlow, 0); % 流量非负% 保存为表格（可选）
regionNames = arrayfun(@(x) sprintf('Region_%d', x), 1:numRegions, 'UniformOutput', false);
trafficTable = array2table(trafficFlow, 'VariableNames', regionNames);
trafficTable.Time = datetime(2023,1,1) + hours(0:hours-1)';%% 2. 数据可视化
figure('Position', [100, 100, 1200, 900]);% (1) 多区域折线图
subplot(2,2,1);
plot(trafficTable.Time, trafficFlow);
xlabel('时间'); ylabel('流量');
title('(1) 各区域流量趋势');
legend(regionNames, 'Location', 'best');
grid on;% (2) 3D曲面图
subplot(2,2,2);
[X,Y] = meshgrid(1:numRegions, 1:hours);
surf(X, Y, trafficFlow);
xlabel('区域'); ylabel('时间'); zlabel('流量');
title('(2) 流量时空分布');
colorbar;% (3) 热力图（按小时聚合）
hourlyAvg = reshape(mean(trafficFlow), 24, []); % 按天聚合
subplot(2,2,3);
imagesc(hourlyAvg);
xticks(1:numRegions); xlabel('区域');
yticks(1:24); ylabel('小时');
title('(3) 每日流量热力图');
colorbar;% (4) 动态可视化（交互式滑块）
subplot(2,2,4);
hPlot = plot(nan, nan, 'LineWidth', 2);
xlabel('区域'); ylabel('流量');
title('(4) 动态展示（拖动滑块）');
xlim([1 numRegions]); ylim([0 100]);% 添加滑块控件
uicontrol('Style', 'slider', 'Position', [100 50 300 20], ...'Min', 1, 'Max', hours, 'Value', 1, ...'Callback', @(src,~) updatePlot(src.Value, hPlot, trafficFlow));% 滑块更新函数
function updatePlot(timeIdx, hPlot, data)set(hPlot, 'XData', 1:size(data,2), 'YData', data(round(timeIdx),:));title(sprintf('时间点 %d: %.1f', round(timeIdx), timeIdx));
end%% 3. 流量预测（LSTM模型）
% 准备训练数据（用前6天预测第7天）
XTrain = trafficFlow(1:end-24, :)';  % 输入：所有区域的历史数据
YTrain = trafficFlow(25:end, :)';    % 输出：滞后24小时的数据% 定义LSTM网络
layers = [ ...sequenceInputLayer(numRegions)lstmLayer(50, 'OutputMode', 'sequence')dropoutLayer(0.2)lstmLayer(25)fullyConnectedLayer(numRegions)regressionLayer];% 训练选项
options = trainingOptions('adam', ...'MaxEpochs', 100, ...'GradientThreshold', 1, ...'Verbose', 0);% 训练模型（实际运行时取消注释）
% net = trainNetwork(XTrain, YTrain, layers, options);% 模拟预测（使用最后24小时作为测试集）
XTest = trafficFlow(end-23:end, :)';
% YPred = predict(net, XTest); % 实际预测代码% 临时用移动平均替代预测结果（示例用）
YPred = movmean(XTest, [3 0]); % 可视化预测结果
figure;
plot(1:numRegions, XTest(:,end), 'bo', 'DisplayName', '实际值');
hold on;
plot(1:numRegions, YPred(:,end), 'r*', 'DisplayName', '预测值');
xlabel('区域'); ylabel('流量');
title('LSTM预测结果示例');
legend; grid on;%% 4. 区域相关性分析
% 计算Pearson相关系数
corrMat = corrcoef(trafficFlow);% 可视化相关性矩阵
figure;
imagesc(corrMat);
colormap('jet'); colorbar;
xticks(1:numRegions); yticks(1:numRegions);
title('区域流量相关性热力图');% 标记高相关性区域对（>0.7）
[row, col] = find(corrMat > 0.7 & corrMat < 1);
for i = 1:length(row)text(col(i), row(i), sprintf('%.2f', corrMat(row(i),col(i))), ...'HorizontalAlignment', 'center', 'Color', 'w');
end% 网络图展示
figure;
G = graph(corrMat > 0.7, 'upper', 'OmitSelfLoops');
plot(G, 'NodeLabel', regionNames, 'EdgeAlpha', 0.3);
title('区域关联网络图');

代码功能说明

数据生成
- 模拟5个区域7天的交通流量数据
- 包含基础流量差异、时间周期效应和随机噪声
可视化模块
- 折线图：展示各区域流量趋势
- 3D曲面：显示时空分布规律
- 热力图：聚合分析每日模式
- 动态图：通过滑块交互查看任意时刻数据
预测模型
- 使用LSTM网络（注释部分为实际训练代码）
- 示例中用移动平均替代预测结果展示流程
相关性分析
- 计算区域间Pearson相关系数
- 热力图+网络图双重可视化

乘客分布热力图：

% 假设乘客请求数据存储在矩阵requests中，行代表区域，列代表时间段
requests = rand(10, 24); % 示例：10个区域，24小时需求% 绘制热力图
figure;
imagesc(requests);
colorbar;
title('乘客需求分布热力图');
xlabel('时间段（小时）');
ylabel('区域编号');
set(gca, 'XTick', 1:24, 'XTickLabel', 1:24);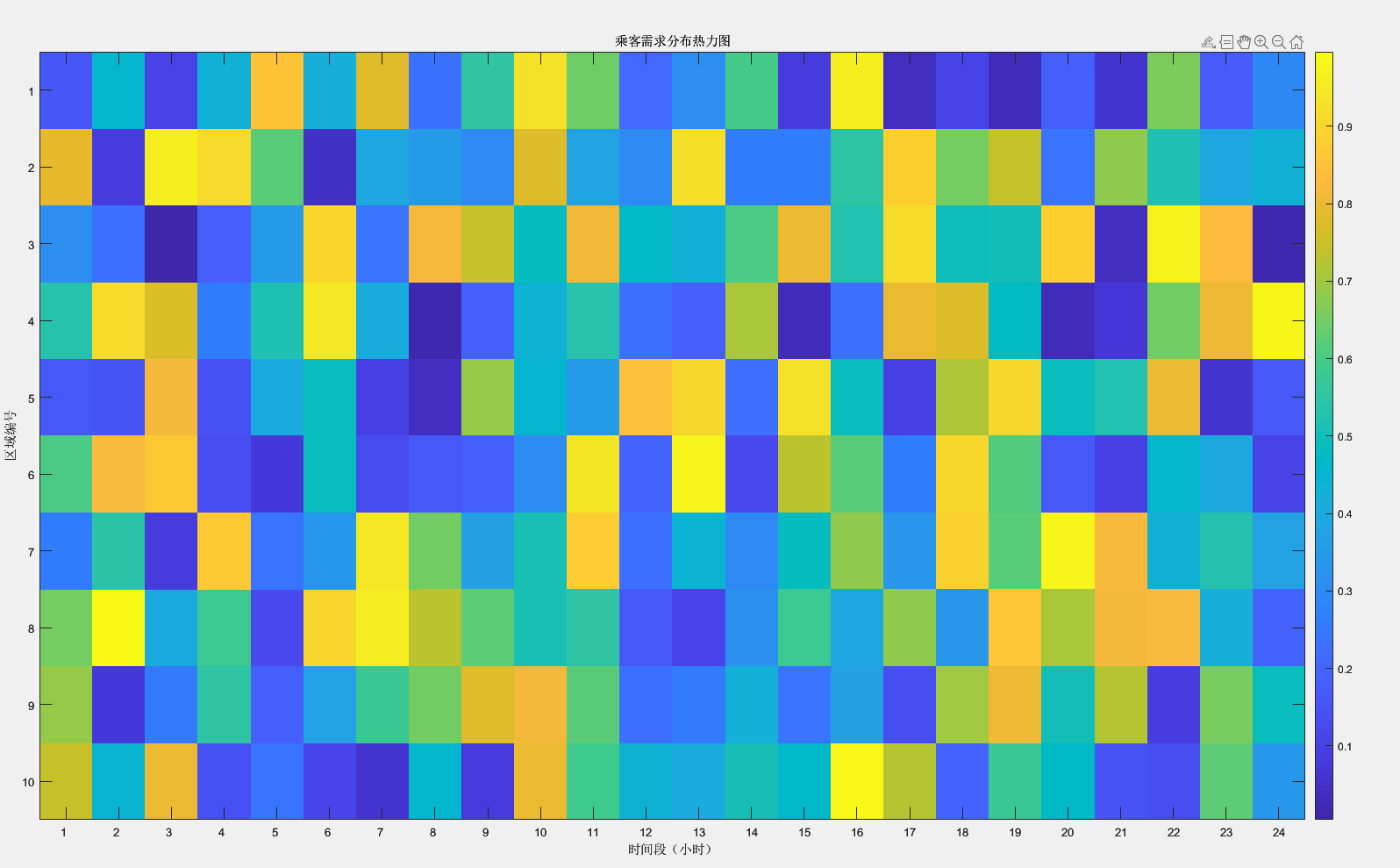

出租车空驶率时间序列图：

% 假设空驶率数据存储在数组idleRates中，对应24小时
idleRates = 0.3 + 0.2 * rand(1, 24); % 示例数据% 绘制时间序列图
figure;
plot(1:24, idleRates, '-o', 'LineWidth', 2);
title('出租车空驶率时间序列');
xlabel('时间段（小时）');
ylabel('空驶率');
grid on;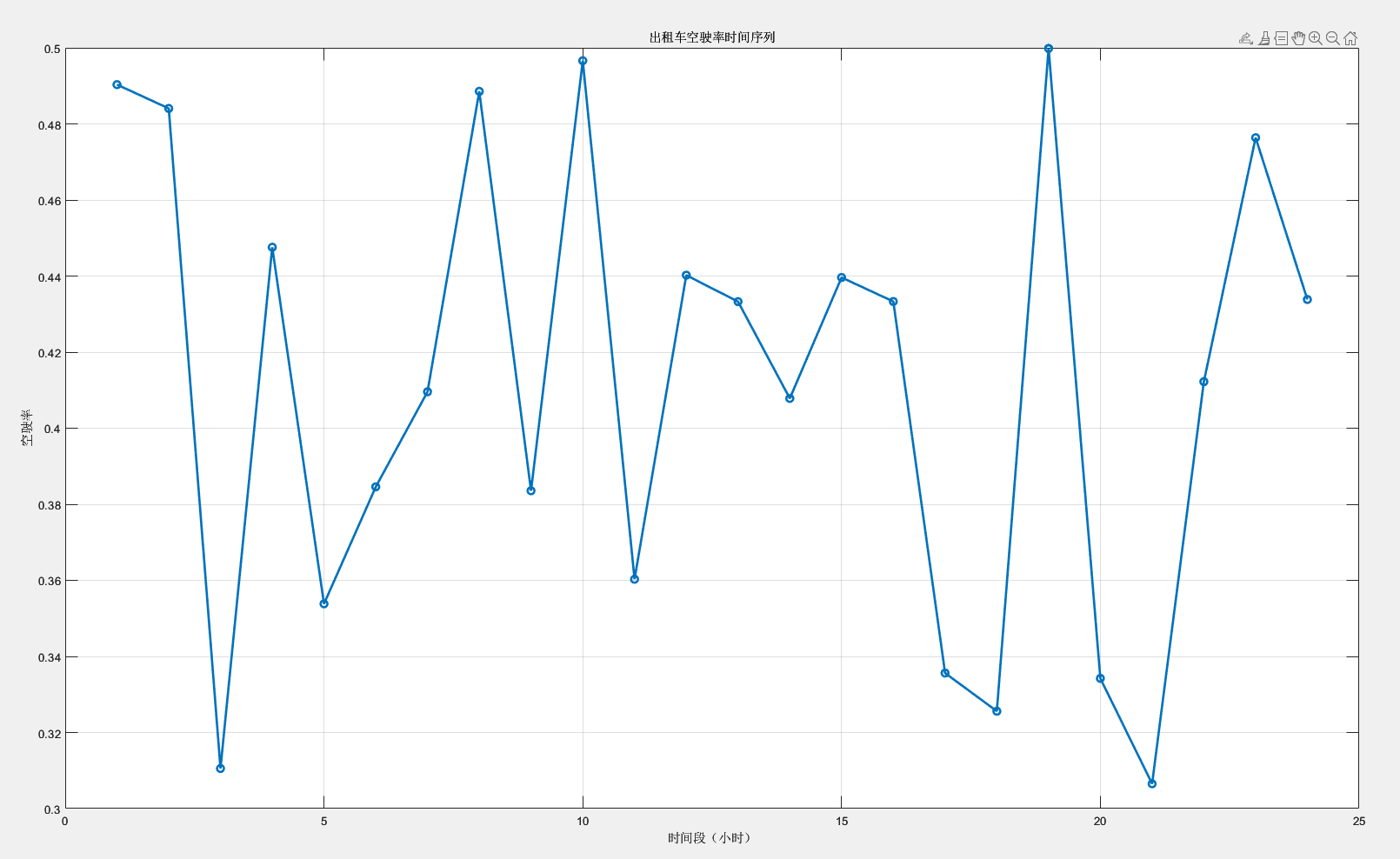

乘客等待时间分布直方图：

% 假设乘客等待时间数据存储在数组waitTimes中
waitTimes = 5 + 10 * rand(1000, 1); % 示例：1000名乘客的等待时间% 绘制直方图
figure;
histogram(waitTimes, 20); % 20个区间
title('乘客等待时间分布直方图');
xlabel('等待时间（分钟）');
ylabel('乘客数量');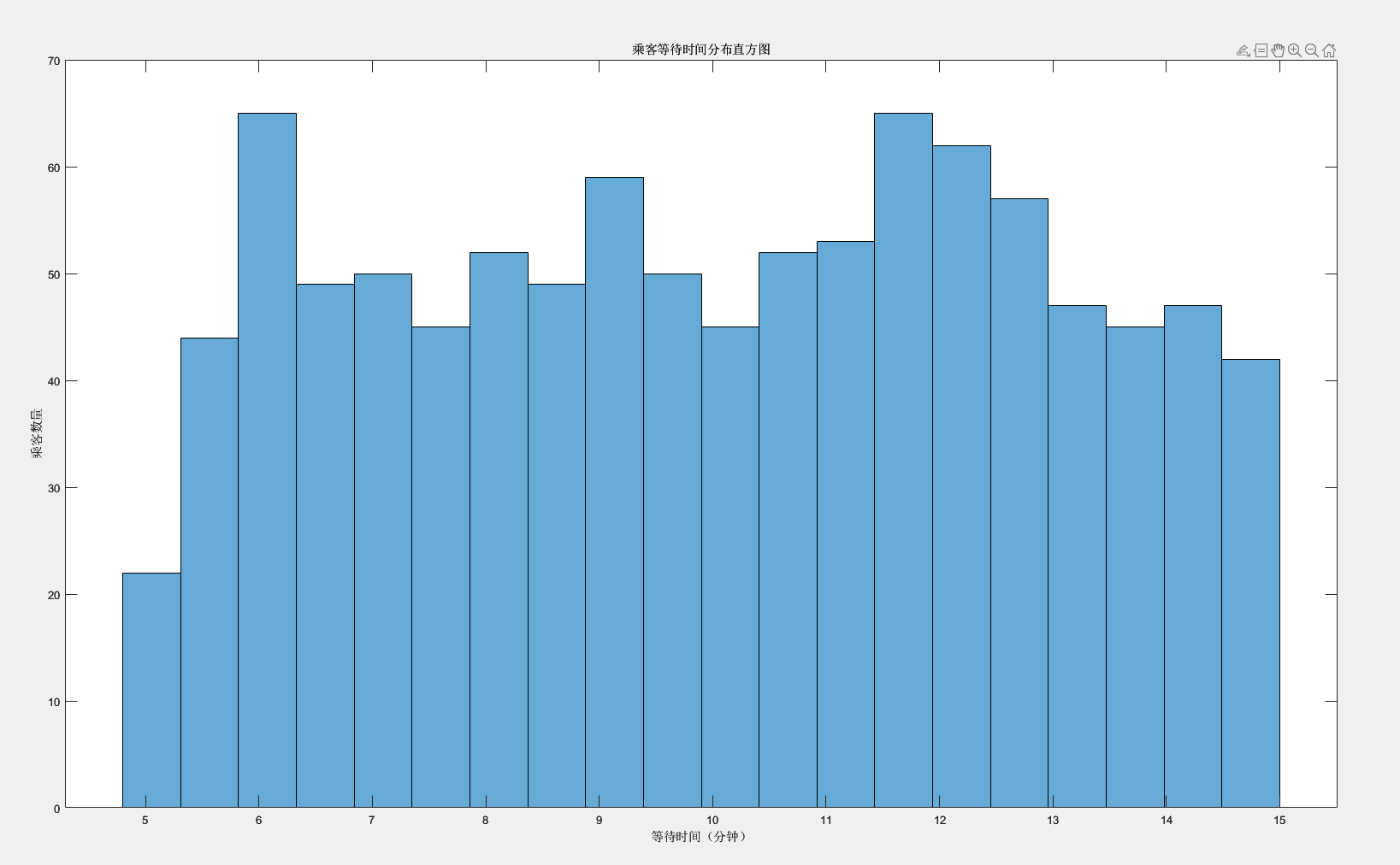

强化学习奖励曲线图:

% 假设奖励数据存储在数组rewards中，对应训练轮次
rewards = cumsum(0.5 + 0.1 * randn(100, 1)); % 示例：100轮训练的累积奖励% 绘制奖励曲线
figure;
plot(1:100, rewards, '-r', 'LineWidth', 2);
title('强化学习奖励曲线');
xlabel('训练轮次');
ylabel('累积奖励');
grid on;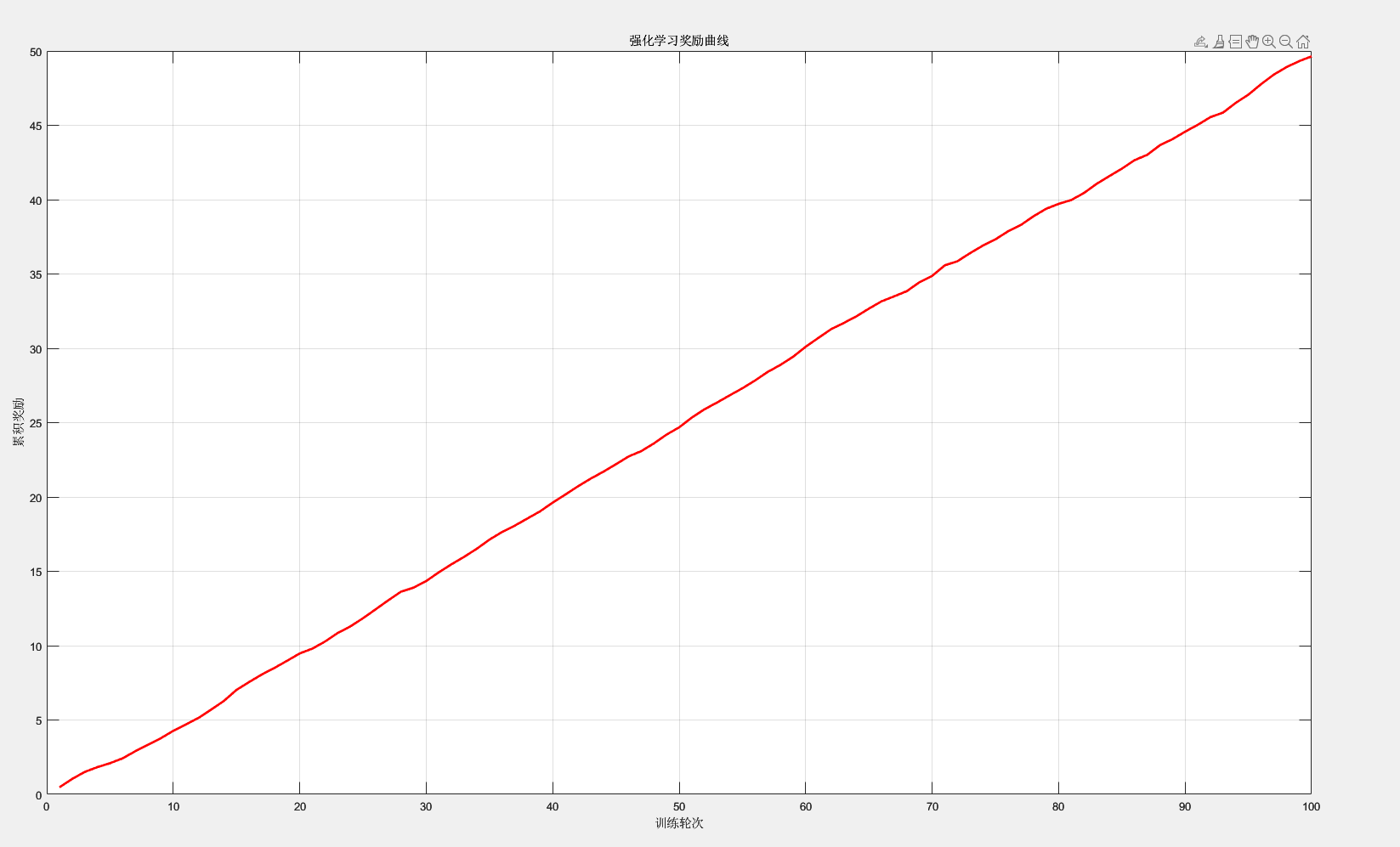

出租车-乘客匹配空间分布图：

% 假设匹配位置数据存储在矩阵matches中，每行代表一个匹配对（出租车x,y；乘客x,y）
matches = [rand(50, 2)*10, rand(50, 2)*10]; % 示例：50个匹配对% 绘制散点图
figure;
scatter(matches(:,1), matches(:,2), 'b', 'filled'); % 出租车位置
hold on;
scatter(matches(:,3), matches(:,4), 'r', 'filled'); % 乘客位置
title('出租车-乘客匹配空间分布');
xlabel('X坐标');
ylabel('Y坐标');
legend('出租车位置', '乘客位置');
grid on;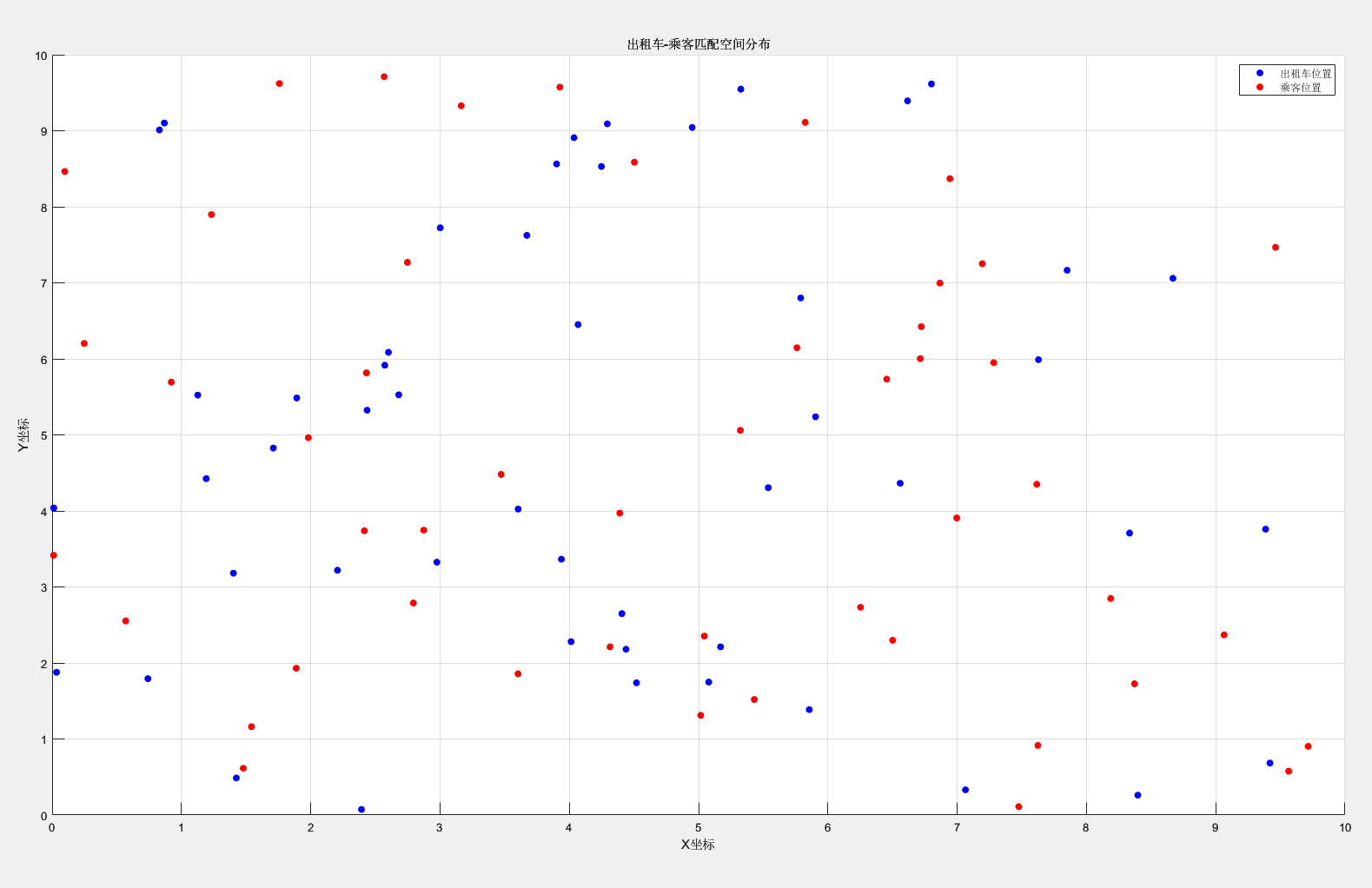

补贴策略效果对比图（柱状图）：

% 假设两种策略下的打车成功率数据
successRates = [0.85, 0.92]; % 策略A和策略B% 绘制柱状图
figure;
bar(successRates);
title('不同补贴策略下的打车成功率对比');
xlabel('补贴策略');
ylabel('打车成功率');
set(gca, 'XTickLabel', {'策略A', '策略B'});
grid on;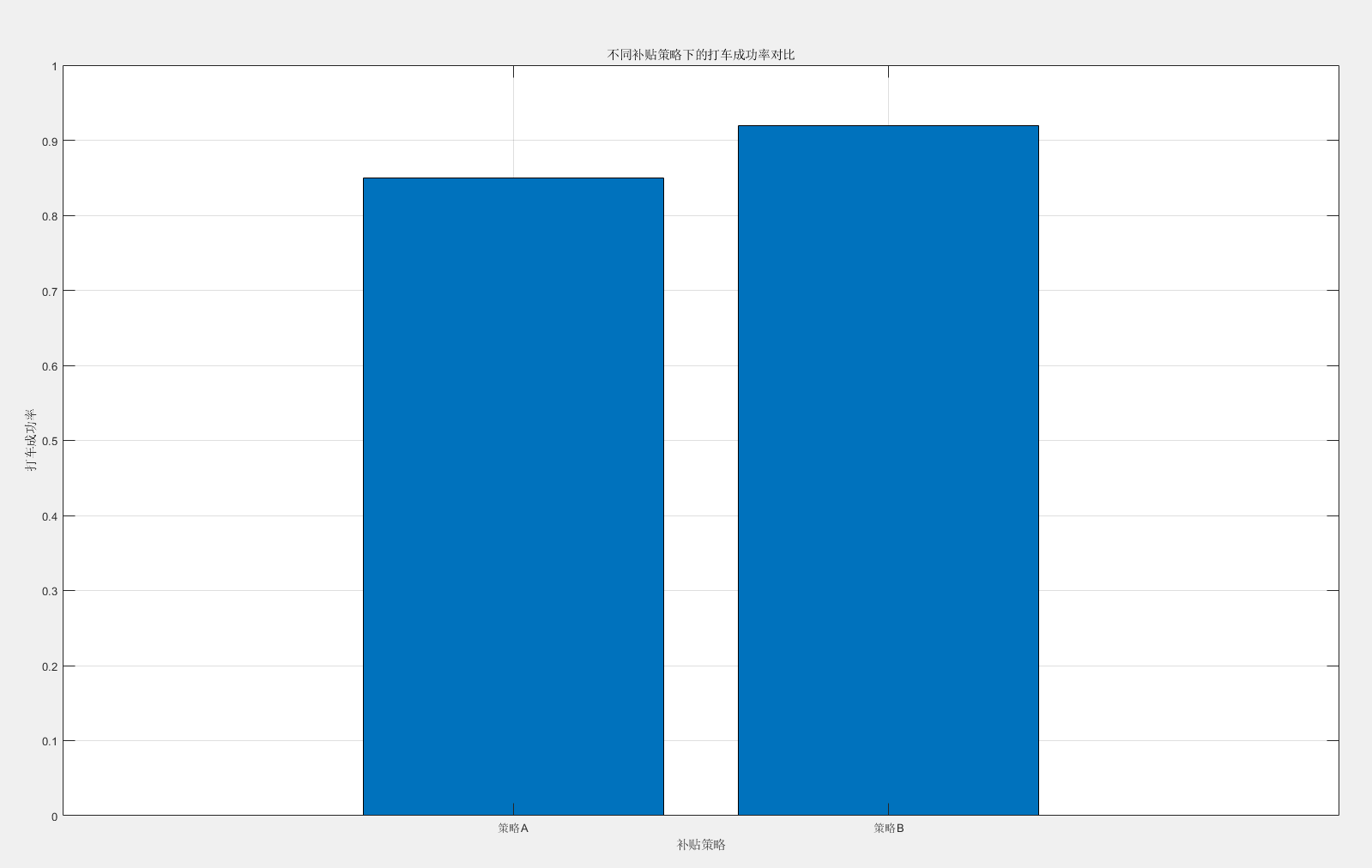

时空交通流量分布：

% 生成模拟数据：10个区域×24小时
[region, time] = meshgrid(1:10, 1:24);
trafficFlow = 5 + 8*sin(time/4) + 3*randn(size(time)); % 添加周期性波动% 创建视频对象
videoFile = 'traffic_3d_surface.mp4';
writerObj = VideoWriter(videoFile, 'MPEG-4');
writerObj.FrameRate = 10; % 高帧率平滑旋转
open(writerObj);% 绘制初始3D曲面
figure('Color', 'white', 'Position', [100, 100, 900, 700]);
h = surf(region, time, trafficFlow, 'EdgeColor', 'none');
colormap(jet); colorbar;
xlabel('区域编号'); ylabel('时间（小时）'); zlabel('交通流量');
title('时空交通流量分布', 'FontSize', 14, 'FontWeight', 'bold');
view(30, 30); % 初始视角% 动态旋转视角（360度）
for az = 30:2:390view(az, 30); % 水平旋转drawnow;frame = getframe(gcf);writeVideo(writerObj, frame);
end% 动态时间轴（固定视角，时间流动）
view(30, 30); % 重置视角
for t = 1:24% 更新曲面数据（模拟实时变化）newData = trafficFlow + 1.5*randn(size(trafficFlow));set(h, 'ZData', newData);title(sprintf('时空交通流量分布（时间=%d:00）', t-1), 'FontSize', 14);% 高亮当前时间切片（用半透明平面标记）hold on;xline = [1 10]; yline = [t t]; zline = [min(newData(:)) max(newData(:))];plot3(xline, yline, zline, 'r-', 'LineWidth', 2); % 时间线hold off;frame = getframe(gcf);writeVideo(writerObj, frame);
endclose(writerObj);
disp(['视频已保存至: ' fullfile(pwd, videoFile)]);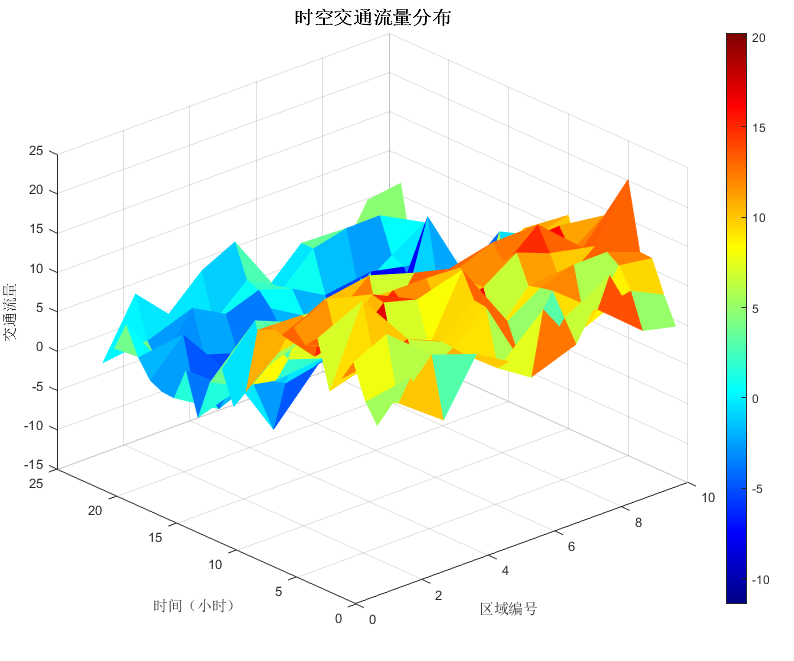

一、乘客视角指标：反映打车体验

1. 匹配率（Matching Rate）

定义：成功打车的乘客比例，反映需求满足程度。
数学公式：

% 假设数据：每小时订单数（D）和成功匹配数（M_actual）
D = [1200, 1500, 1000, ...]; % 总订单数（向量，长度24小时）
M_actual = [1080, 1350, 950, ...]; % 成功匹配数
matching_rate = M_actual ./ D; % 计算每小时匹配率

2. 平均等待时间（Average Waiting Time）

定义：乘客从发起订单到被匹配的平均时间（分钟）。
数学公式：
[
W_t = \frac{1}{N_t} \sum_{i=1}^{N_t} w_{i,t}
]
其中 ( N_t ) 为 ( t ) 时刻成功匹配的订单数，( w_{i,t} ) 为第 ( i ) 个订单的等待时间。
MATLAB实现：

% 假设数据：每小时等待时间列表（每行代表一小时的等待时间数组）
waiting_times = {[5, 8, 10], [3, 6, 7, 9], [12, 15], ...}; % 嵌套元胞数组
avg_waiting_time = zeros(1, 24);
for t = 1:24if ~isempty(waiting_times{t})avg_waiting_time(t) = mean(waiting_times{t});elseavg_waiting_time(t) = NaN; % 无数据时标记为NaNend
end

3. 订单取消率（Cancellation Rate）

定义：因等待时间过长而取消的订单比例。
数学公式：
[
C_t = \frac{\text{取消订单数}_t}{\text{总订单数}_t}
]
MATLAB实现：

cancelled_orders = [120, 150, 80, ...]; % 每小时取消订单数
cancellation_rate = cancelled_orders ./ D;

二、司机视角指标：反映收入与效率

1. 空驶率（Idle Rate）

定义：司机空闲时间占总运营时间的比例。
数学公式：
[
I_t = \frac{\text{空闲时间}_t}{\text{总运营时间}_t}
]
MATLAB实现：

% 假设数据：每小时空闲时间（分钟）和总运营时间（分钟）
idle_time = [30, 45, 20, ...]; % 空闲时间
total_operation_time = 60 * ones(1, 24); % 假设每小时运营60分钟
idle_rate = idle_time ./ (total_operation_time * 60); % 转换为比例

2. 平均收入（Average Earnings）

定义：司机每小时的平均收入（元）。
数学公式：
[
E_t = \frac{\text{总收入}_t}{\text{活跃司机数}_t}
]
MATLAB实现：

total_earnings = [200, 250, 180, ...]; % 每小时总收入（元）
active_drivers = [800, 850, 700, ...]; % 每小时活跃司机数
avg_earnings = total_earnings ./ active_drivers;

3. 接单距离（Pickup Distance）

定义：司机从当前位置到乘客上车点的平均距离（公里）。
数学公式：
[
P_t = \frac{1}{N_t} \sum_{i=1}^{N_t} p_{i,t}
]
其中 ( p_{i,t} ) 为第 ( i ) 个订单的接单距离。
MATLAB实现：

pickup_distances = {[1.2, 1.5, 1.8], [0.8, 1.0, 1.2, 1.5], [2.0, 2.5], ...};
avg_pickup_dist = zeros(1, 24);
for t = 1:24if ~isempty(pickup_distances{t})avg_pickup_dist(t) = mean(pickup_distances{t});elseavg_pickup_dist(t) = NaN;end
end

三、平台视角指标：反映运营效率

1. 订单匹配时间（Matching Time）

定义：平台从接收订单到完成匹配的平均时间（秒）。
数学公式：
[
T_t = \frac{1}{N_t} \sum_{i=1}^{N_t} t_{i,t}
]
其中 ( t_{i,t} ) 为第 ( i ) 个订单的匹配时间。
MATLAB实现：

matching_times = {[10, 12, 15], [8, 10, 12, 14], [20, 25], ...};
avg_matching_time = zeros(1, 24);
for t = 1:24if ~isempty(matching_times{t})avg_matching_time(t) = mean(matching_times{t});elseavg_matching_time(t) = NaN;end
end

2. 供需比（Supply-Demand Ratio）

定义：空闲出租车数量与乘客需求的比例，反映市场紧俏程度。
数学公式：
[
R_t = \frac{\text{空闲出租车数}_t}{\text{总订单数}_t}
]
MATLAB实现：

idle_taxis = [700, 750, 600, ...]; % 每小时空闲出租车数
supply_demand_ratio = idle_taxis ./ D;

3. 区域覆盖率（Coverage Rate）

定义：平台服务覆盖的区域面积与总城市面积的比例。
数学公式：
[
\text{Coverage}_t = \frac{\text{有订单的区域数}_t}{\text{总区域数}}
]
MATLAB实现：

% 假设数据：每小时有订单的区域数（需结合GIS数据）
covered_areas = [50, 55, 48, ...]; % 示例值
total_areas = 100; % 城市总区域数
coverage_rate = covered_areas / total_areas;

四、社会视角指标：反映资源利用效率

1. 车辆利用率（Vehicle Utilization）

定义：出租车实际运营时间占总时间的比例。
数学公式：
[
U_t = \frac{\text{运营时间}_t}{\text{总时间}_t}
]
MATLAB实现：

operation_time = [50, 55, 45, ...]; % 每小时运营时间（分钟）
total_time = 60 * ones(1, 24); % 每小时总时间（分钟）
vehicle_utilization = operation_time ./ total_time;

2. 碳排放量（Carbon Emission）

定义：出租车运营产生的二氧化碳排放量（吨）。
数学公式：
[
\text{Emission}t = \sum{i=1}^{N_t} d_{i,t} \cdot \text{emission_factor}
]
其中 ( d_{i,t} ) 为第 ( i ) 个订单的行驶距离，( \text{emission_factor} ) 为单位距离排放量（如0.2 kg/km）。
MATLAB实现：

order_distances = {[5, 8, 10], [4, 6, 7, 9], [12, 15], ...}; % 每小时订单行驶距离（km）
emission_factor = 0.2; % kg/km
total_emission = zeros(1, 24);
for t = 1:24if ~isempty(order_distances{t})total_emission(t) = sum(order_distances{t}) * emission_factor / 1000; % 转换为吨elsetotal_emission(t) = 0;end
end

五、指标综合应用示例

1. 指标可视化（MATLAB代码）

% 绘制匹配率、等待时间、空驶率随时间变化
figure;
subplot(3,1,1);
plot(1:24, matching_rate, '-o', 'LineWidth', 2);
title('匹配率');
xlabel('小时');
ylabel('比例');
grid on;subplot(3,1,2);
plot(1:24, avg_waiting_time, '-r', 'LineWidth', 2);
title('平均等待时间（分钟）');
xlabel('小时');
ylabel('时间');
grid on;subplot(3,1,3);
plot(1:24, idle_rate, '-g', 'LineWidth', 2);
title('空驶率');
xlabel('小时');
ylabel('比例');
grid on;