问题描述：

两个相同的硬币，半径都是 $r$。一个硬币（称为“动硬币”）沿着另一个固定不动的硬币（“静硬币”）的外边缘无滑动地滚动一圈，回到起始位置。问：动硬币自身旋转了几圈？

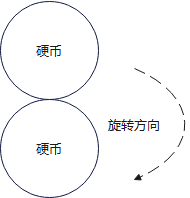
答案是：2圈

这有点奇怪，因为一个硬币的周长是 $2\pi r$，另一个硬币的周长也是 $2\pi r$，动硬币绕着你静硬币走一圈，静硬币展开成一条直线距离也就 $2\pi r$，怎么就要转两圈呢？

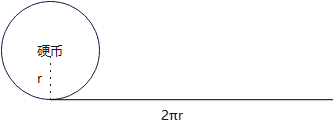
这答案看起来违反直觉，所以叫悖论

误区澄清

直观上看，静硬币展开成一条直线距离也就 $2\pi r$，所以动硬币应该只转一圈

这个想法基于一个假设：动硬币是沿着一个长度为 $2\pi r$ 的直线滚动。但实际上静硬币不能就这么直接展开成一条线，它俩不等价

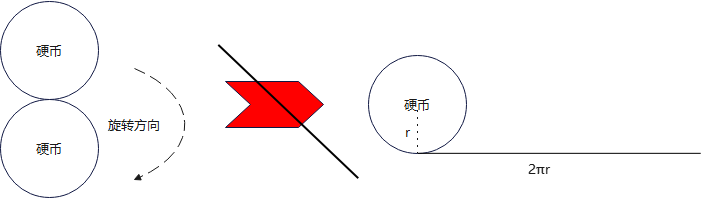
下面来详细解释下

直观解释

首先，如果动硬币沿着一条直线滚动，那距离确实就等于静硬币的周长

但现在它是沿着一个圆形路径滚动，路径的半径是两个硬币半径之和

$$r+r=2r$$

所以动硬币的中心走过的路径是一个半径为 $2r$ 的圆，周长为

$$C_{path}=2\pi \times (2r)=4\pi r$$

动硬币的周长是 $2\pi r$，所以它需要自转

$$\frac{4\pi r}{2\pi r}=2圈$$

所以如果把动硬币走过的距离看成直线，应该是下图

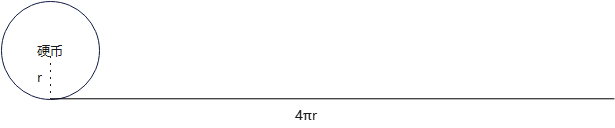
为什么直觉会错

被接触点迷惑了！

• 我们以为动硬币是沿着静硬币的周长滚动，所以距离是 $2\pi r$
• 但实际上，滚动的距离是动硬币中心移动的路径长度，而不是接触点的轨迹长度

就像一辆车轮半径为 $r$ 的车，车轮转一圈，车向前移动 $2\pi r$ ，但车轮中心也移动了
$2\pi r$ 。同理，这里车（动硬币）是绕着一个大圆（半径 $2r$）走，所以中心走了 $4\pi r$，自然要转两圈

所以看圆的滚动距离，要看中心点移动的距离，而不是接触点的轨迹长度

两种旋转的来源

动硬币的自转两圈可以分解为两部分：

• 由于平移产生的旋转（1圈）：好比动硬币沿着一条长 $2\pi r$ 的直线滚动，它会转1圈
• 由于路径是圆形而产生的额外旋转，也就是自转（1圈）：即使动硬币不滚动，只是平移着绕静止硬币转一圈，它的朝向也会相对于固定空间旋转一整圈（就像月亮绕地球转，始终有一面向着地球，但在空间中它其实自转了一圈）

当 平移 + 自转 同时发生时，这两个旋转叠加，总共就是 2 圈

拓展

当动硬币半径为 $r$， 而静止硬币的半径是 $3r$ 时，动硬币绕着静止硬币的外边缘无滑动地滚动一圈，回到起始位置。问：动硬币自身旋转了几圈？

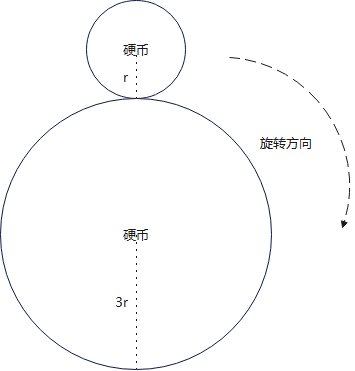
答案是：4圈

同样，动硬币绕静止硬币中心走一圈的距离取决于它自身的中心轨迹，既然动硬币紧贴静止硬币外侧滚动，它的中心实际上是在距离静止硬币中心
$$r+3r=4r$$
的位置移动。因此，动硬币的中心将沿着一个半径为 $4r$ 的圆周运动

这个圆周的长度（即动硬币中心走过的路径长度）可以通过下面的公式计算：
$$C=2\pi \times (半径)=2\pi \times (4r)=8\pi r$$
所以，动硬币走过的路径长度是 $8\pi r$。这意味着，相对于地面，动硬币会自转四圈：
$$\frac{8\pi r}{2\pi r}=4$$

同样，从旋转来源的视角：

• 由于平移产生的旋转：好比动硬币沿着一条长 $6\pi r$ 的直线滚动，它会转 3 圈
• 由于路径是圆形而产生的额外旋转，也就是自转（1圈）

平移 + 自转 同时发生，这两个旋转叠加，总共就是 4 圈