2025.7.27周报
- 一、文献阅读
- 题目信息
- 摘要
- 创新点
- 实验
- 一、半变异函数拟合
- 二、普通克里金插值
- 三、结果对比分析
- 四、实验结果
- 结论
- 不足以及展望
一、文献阅读
题目信息
- 题目: Application of a semivariogram based on a deep neural network to Ordinary Kriging interpolation of elevation data
- 期刊: PLOS ONE
- 作者: Yang Li, Zhong Baorong, Xu Xiaohong, Liang Zijun
- 发表时间: 2022
- 文章链接: https://journals.plos.org/plosone/article?id=10.1371/journal.pone.0266942
摘要
普通克里金是常用的空间插值方法,其半变异函数的拟合效果对插值精度有显著影响。常用的半变异函数模型有高斯、球形和指数模型,一般需手动比较和调整参数来选择最优模型。现有的半变异函数拟合方法存在手动分析选择模型和受所选模型限制的问题。为减少手动选择模型的繁琐过程,提高拟合优度,本文提出用DNN模拟半变异函数进行插值。本文提出了一种基于深度神经网络和普通克里金的空间插值新方法。通过Python的Keras建立DNN模型拟合半变异函数,以高程数据为案例研究。将该方法的插值结果与传统的指数、高斯和球形模型进行对比,结果表明基于DNN的方法克里金方差更小,插值结果更接近理论值,还能简化半变异函数分析过程。这解决了传统半变异函数拟合的问题,提高了插值精度,简化了分析过程,对地理统计和空间插值领域有重要意义。
创新点
提出用DNN模拟半变异函数进行OK插值,理论上可拟合所有函数,能获得最佳拟合的半变异函数,提高插值精度。
实验
将深度神经网络与普通克里金法相结合,这个模型的选择和拟合效果直接影响最终插值的精度。实验选取了四个独立的 50x50 区域(4个区域)作为高程数据测试区 。
实验可分为半变异函数拟合、普通克里金插值 和 结果对比分析三个阶段
一、半变异函数拟合
研究对比了三种模型的拟合效果:DNN 模型、高斯模型和指数模型。
DNN 模型构建:使用基于 Python 的 TensorFlow 和 Keras 库来搭建 DNN 模型。设置了 15 个全连接层。输入层和输出层的神经元数量均为 1 。中间隐藏层使用 Relu 激活函数,以加快神经元拟合速度;输入和输出层则使用 Softplus 函数;优化器选择 Adam,因为它训练时间短且效果好。损失函数为均方误差。
半变异函数遵循地理学第一定律约束。在训练过程中监控模型的梯度,一旦出现负梯度,就选择上一步训练得到的全正梯度模型,以确保函数单调递增 。验证采用了 k-折交叉验证(k=10)。将用于拟合的数据集分成 10 份,每次用 9 份作为训练集,1 份作为验证集,共进行 10 次训练,以优化模型权重。对于高斯模型和指数模型,研究使用了最小二乘法来拟合 80% 的数据点 。
二、普通克里金插值
无论是使用 DNN 还是传统模型得到的半变异函数,后续的普通克里金插值流程是统一的:
- 、将未知点与已知样本点之间的距离代入已拟合好的半变异函数模型(DNN 模型、高斯模型或指数模型),得到它们之间的半变异函数值 。
- 利用得到的半变异函数值构建克里金方程组,求解得到每个已知样本点对于未知点的权重系数
λ。 - 通过加权求和的方式,计算出未知点的估算值 。
- 对所有待插值的点重复以上步骤
三、结果对比分析
为了全面评估 DNN-OK 方法的性能,研究设置了多个评估指标,并与高斯-OK和指数-OK进行对比。
在进行克里金插值前,对四个区域的样本集进行了柯尔莫哥洛夫-斯米尔诺夫检验(Kolmogorov-Smirnov test),计算 P-value。结果显示所有区域的 P-value 均大于 0.05,表明样本服从正态分布,适合进行 OK 插值 。
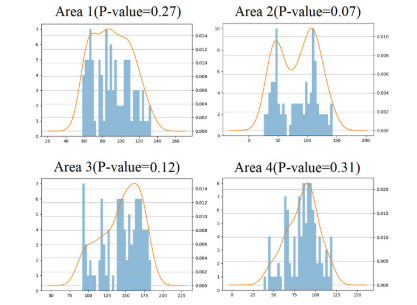
四、实验结果
拟合效果:
使用决定系数 R2R^2R2 来评估各个模型对半变异函数的拟合效果。R2R^2R2 越接近 1,说明模型的拟合效果越好。分别在训练集(80%)和测试集(20%)上计算了 R2R^2R2 值 。
在训练集上,DNN 模型的 R2R^2R2 值在所有四个区域中均显著高于高斯和指数模型,达到了 0.98 以上。在测试集上,DNN 模型的泛化能力同样表现出色,其 R2R^2R2 值也普遍优于传统模型。这表明 DNN 能够更精确地捕捉数据的空间相关性结构。
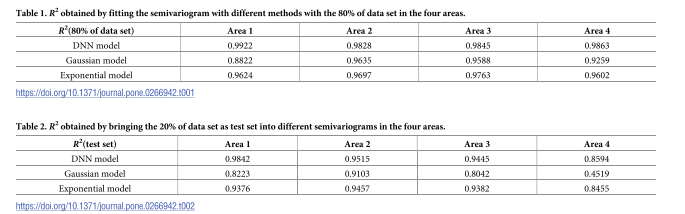
克里金方差:
该指标衡量插值结果与理论结果的偏离程度。克里金方差越小,说明插值结果越接近理论上的最优估计 。DNN-OK 方法在所有四个区域产生的平均克里金方差都是最小的。例如,在区域 1,DNN-OK 的方差为 52.52,而高斯-OK 和指数-OK 分别为 90.87 和 92.42 。这证明了 DNN-OK 的结果在理论上更稳定,更接近最优无偏估计。
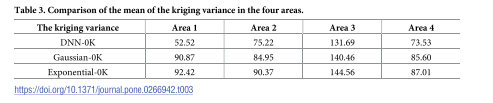
插值精度:
通过将插值结果与原始数据的真实值进行比较,计算 MAE 和 RMSE,这两个值越小,代表插值精度越高。DNN-OK 在四个区域中的三个区域的 MAE 值均低于其他两种方法;DNN-OK 在所有四个区域的 RMSE 值几乎都取得了最好或次好的结果,显著改善了插值精度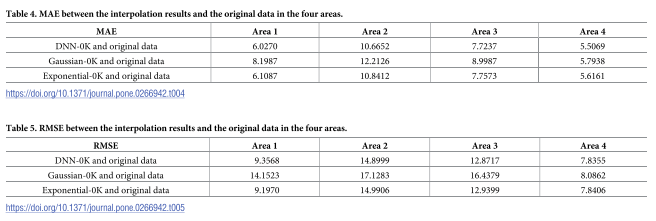
结论
DNN能拟合出最优半变异函数,反映最佳空间相关性,可替代多数其他半变异函数,简化分析过程;该方法使克里金方差最小,优化了OK算法;虽需更多计算时间,但可节省人工分析时间。
不足以及展望
基于DNN拟合的半变异函数需要更多计算时间,对GPU性能要求较高。可进一步优化DNN模型,减少计算时间。


)



系统)


labelstudio实现自动化标注)









