一，卷积后的特征图大小计算

众所周知，提到深度学习，必不可少的会提及卷积，那么如何计算卷积之后的图片大小呢？

下图呈现：

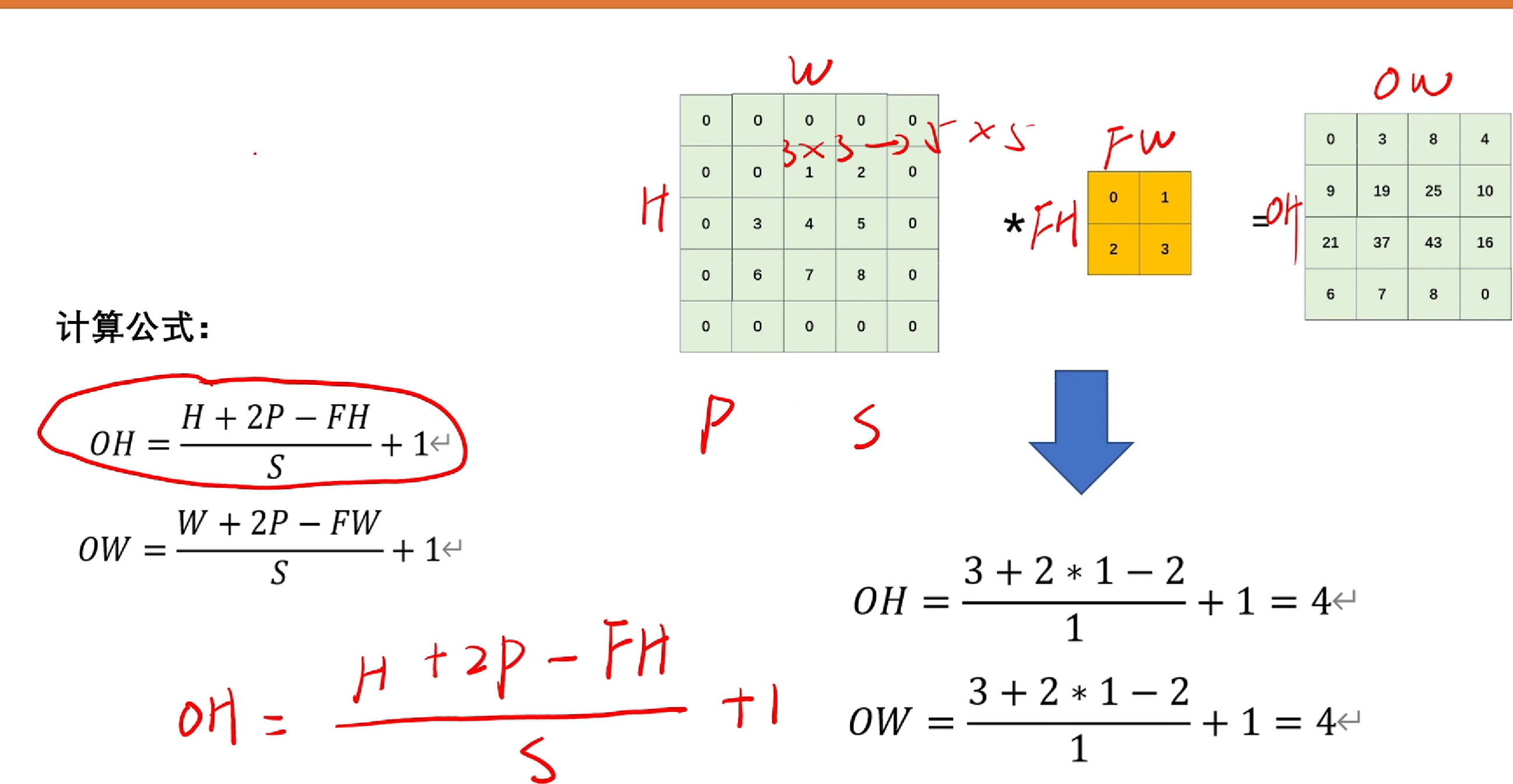
如图，我们令FH，FW为原图像的长度FH*FW。P为padding的长度（假如padding=1,则3*3变成5*5），H,W为图像padding后的长度。OH,OW为卷积后的图像长度。

ps:计算结果为小数的话向下取整。

练习题：

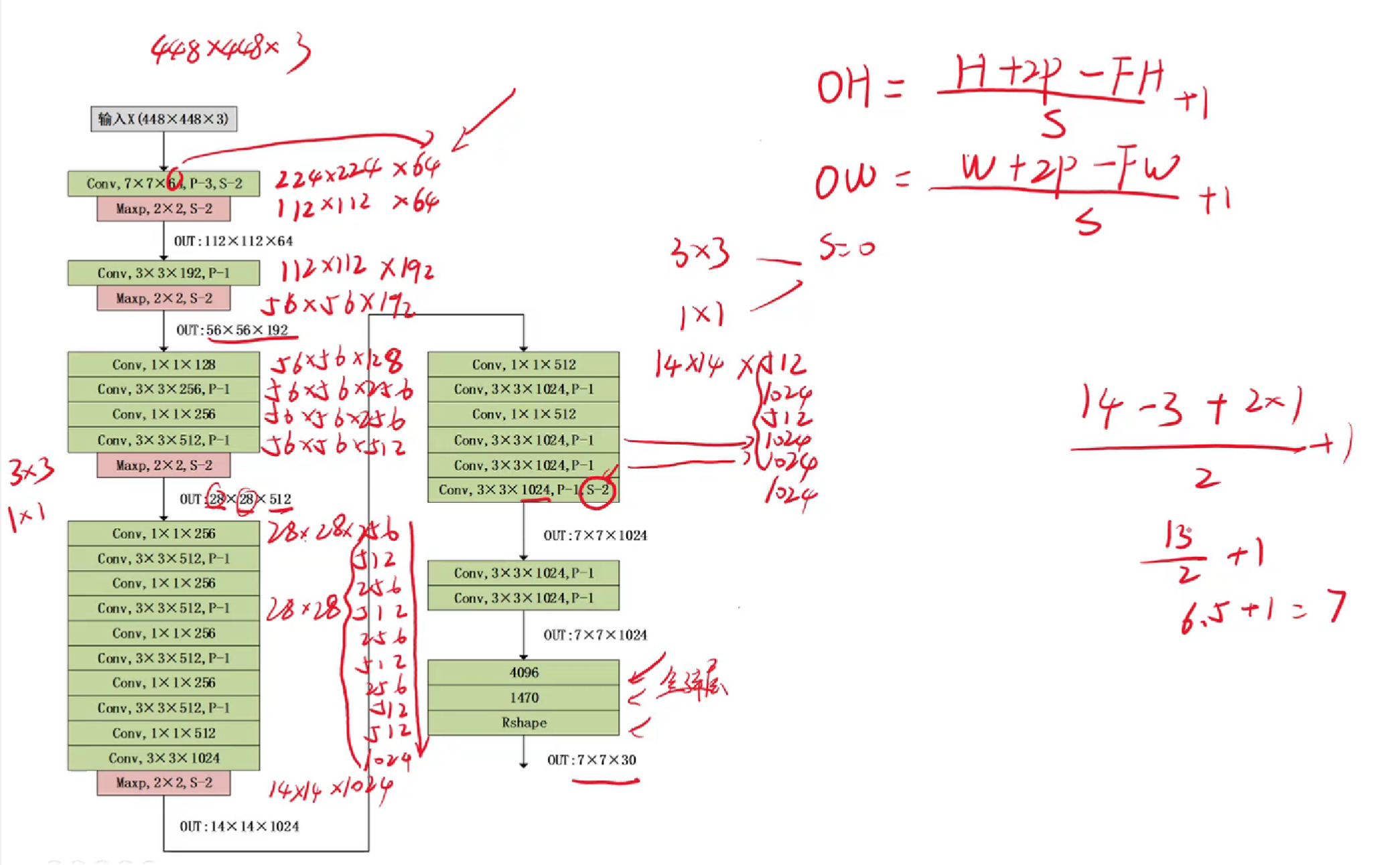
答案：

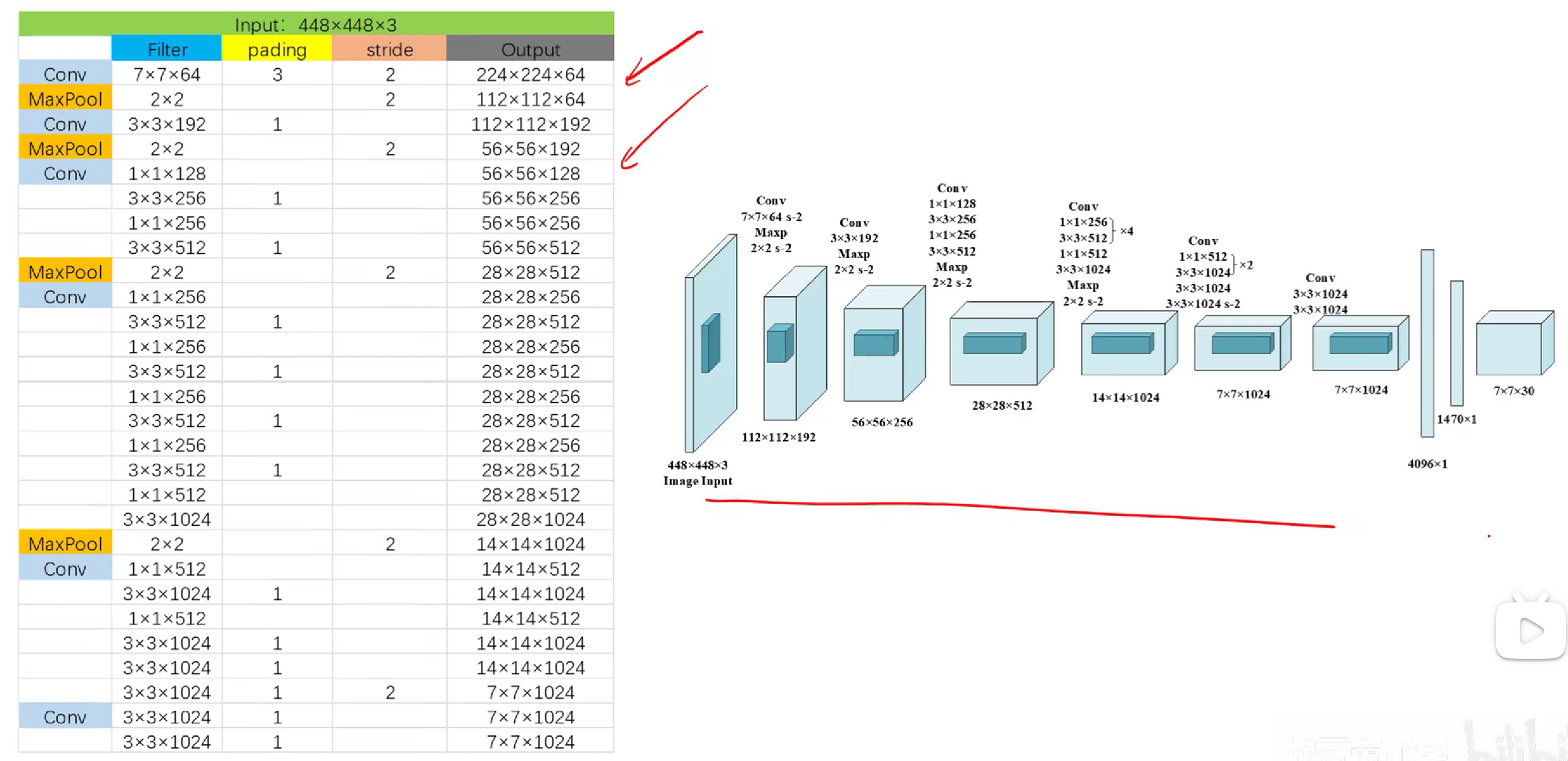
小tip:(1)单阶段检测：分类和检测同时做----速度快

(2)双阶段检测：先分类，再抠图给检测器做检测---精度高

池化，下采样，上采样概念区分：

池化：一种特殊的采样操作，通常用于减少特征图的空间尺寸，常见的有最大池化和平均池化。
下采样：将数据的空间尺寸减少的操作，池化是一种常见的下采样方法。
上采样：将数据的空间尺寸增加的操作，常见于生成更高分辨率的图像或特征图。

卷积，池化会使得模型对图像的感受野不断增大。

二，深刻理解yolov1模型

不管现在发展到了yolov几，要想深刻理解yolo模型的本质设计，就要回到yolov1~yolov3.

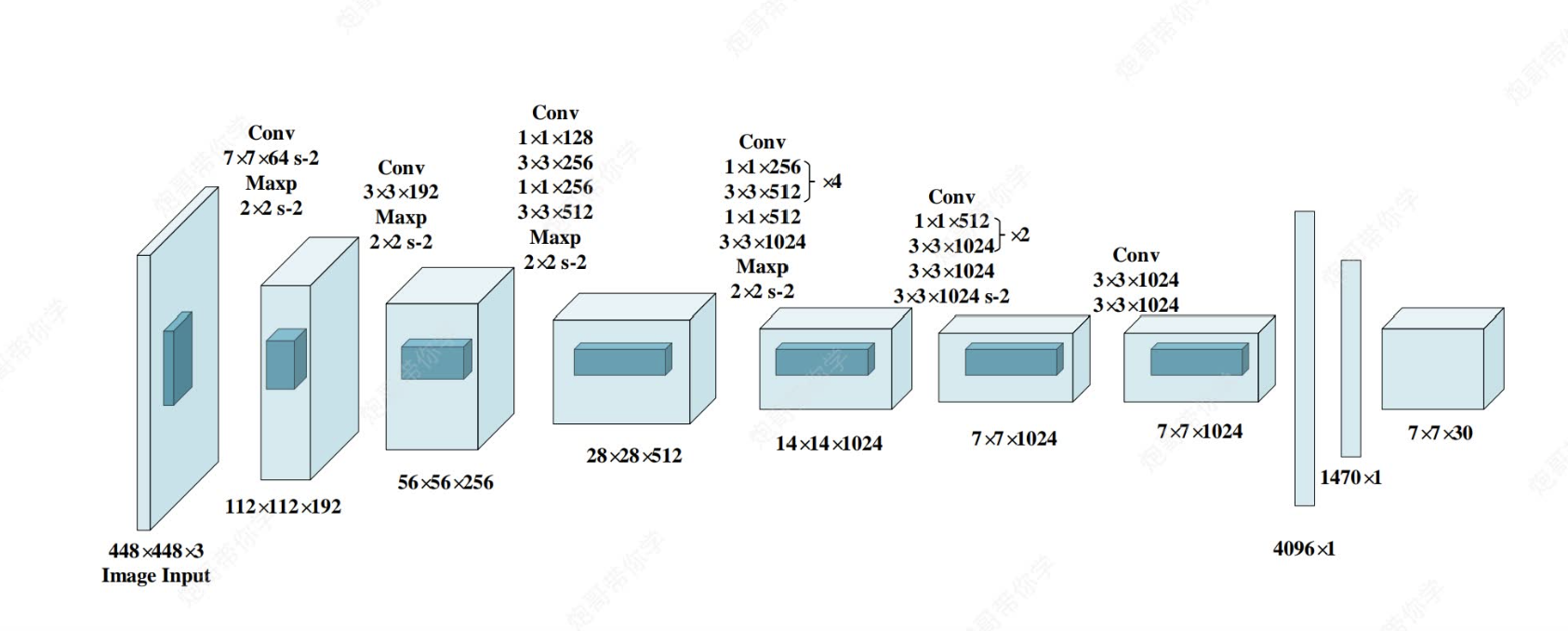
上图为yolov1的网络模型图，其中都是采用和CNN一样的思路（卷积+激活函数+池化+最后全连接层），但是和CNN不一样的是，CNN全连接层最后通过softmax函数可以直接输出我们分类各类别的概率来完成任务，但是yolo中最后全连接层输出的只是7×7×30的向量，他是怎么实现对原图的目标识别与类别检测的呢？(｀ﾍ´)=3

解答：
首先，我们需要理解7*7*30这个向量，他的意思是有7*7个格子，每个格子有30个向量（如下图）（包含30个信息，为什么是30个呢？稍后会说）

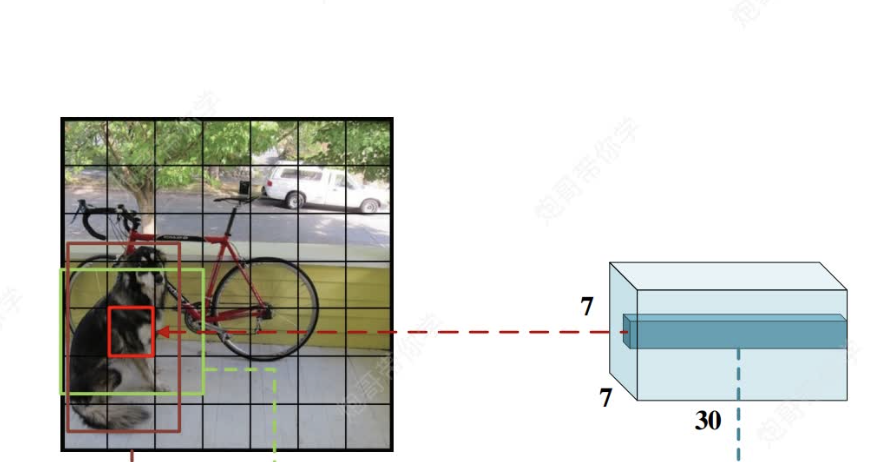
然后这个7*7的向量会被映射到原图448*448 ，将原图划分为49个格子（注意，不是真的划分，是一种映射），每个格子对应原图的一块区域。

对每个区域信息的理解

然后，这时你可能会想每个格子会有原图该区域的检测信息，理解正确，但是要注意，每个格子并不只有该区域的信息，而是都具有全图像全局信息，为什么呢？（这里是理解难点）

由CNN的知识可知，通过层层卷积和池化操作，输出的每个向量信息都具有拥有全局感受野（Global Receptive Field）。

特征表示的层次性和抽象性：
- 深度卷积网络通过多层卷积和池化操作，逐步提取图像的层次化特征。低层特征（靠近输入层）通常对应边缘、纹理等简单模式，感受野较小。高层特征（靠近输出层）则对应更复杂、更抽象的概念，如物体部件、物体类别等，感受野更大。
- 当信息传递到网络的最后几层，形成用于预测的77特征图时，每个特征图上的值（对应一个网格单元）已经包含了非常高级和抽象的信息。这些信息不仅仅是简单的像素叠加，而是通过复杂的非线性变换学习到的、对目标检测任务有用的表示。
- 即使感受野覆盖了整个图像，这些高级特征对于“当前网格单元中心是否有特定类别的物体”这个问题来说，仍然是非常相关的。例如，图像其他部分的物体、背景、甚至物体的上下文信息，都可以帮助模型判断当前网格单元内的区域是否更可能包含某个特定类别的物体（比如，如果网格单元区域看起来像车轮，而图像其他部分有车身，那么它属于车的概率就更高）。
局部信息的权重和定位：
- 虽然全局信息被整合，但模型在学习过程中会自动学习到哪些信息对于当前网格单元的预测更重要。对于“当前网格单元中心是否有物体”的判断（置信度分数 Pr(Object) * IoU），模型会赋予网格单元直接覆盖区域的特征更高的权重。
- 对于边界框坐标（bx, by, bw, bh）的预测，模型学习到的回归函数也会主要关注网格单元覆盖区域的特征来精确定位。全局感受野提供上下文和背景信息，帮助更精确地定位（例如，避免将目标框错误地延伸到背景区域），但最终的坐标预测仍然是以网格单元为中心，并受其局部特征主导的。
注意力机制（隐式）：
- 可以将深度学习模型看作一种隐式的注意力机制。在训练过程中，模型通过反向传播学习，会“关注”那些对预测目标（即当前网格单元是否包含物体及其类别和位置）最有用的特征。即使感受野很大，模型也会学习到，对于当前网格单元的预测任务，只有来自其中心区域及其附近的信息才是最关键的。
网格划分的设计：
- YOLOv1的设计本身就是将图像划分为网格，并让每个网格单元负责其中心区域。网络在训练时会学习到这种责任分配。因此，即使特征具有全局感受野，网络的最终输出（通过全连接层和Sigmoid函数）被训练成主要反映对应网格单元责任区域内的内容。

简单类比：
想象一下，你要判断一张照片的左上角（一个网格单元负责的区域）是否有一只猫。你不仅仅看左上角，你还会看看整个照片的上下文（比如背景是在室内还是室外，是否有其他动物，整体色调等）。这些全局信息（整个照片）帮助你做出更准确的判断（左上角是否有猫，以及是什么类型的猫），但你的最终判断仍然主要基于左上角区域本身的内容。深度学习模型在做类似的事情，它利用全局上下文信息来增强对局部区域的判断能力。

因此，全局感受野并非坏事，它提供了宝贵的上下文信息，有助于提高检测和分类的准确性，同时模型通过学习能够有效地将注意力集中在需要负责的局部区域上。

也就是说，虽然每个格子对应原图的一块区域而已，但是他们都拥有全局感受野（目的：更好进行上下文联系识别），然后通过权重定位更加关注原图该区域的信息识别（注意力机制有点像）。

回到上文，我们将这个7*7的向量会被映射到原图448*448 ，将原图划分为49个格子（注意，不是真的划分，是一种映射），每个格子对应原图的一块区域后，每个格子都包含30个信息，分别是两个检测框（当初设计是为了提高准确率）的（中心坐标x,y,宽高w,h,及其对应的检测置信度c）*2共10个，然后还有要识别的20个类别的概率（两个检测框共用概率值）共30个。

之后，每个格子都会生成2个检测框，只是如果置信度低于我们认为设定的阈值，会被直接不画出检测框。然后剩下的框会进行非极大值抑制，最终产生概率最高的框。

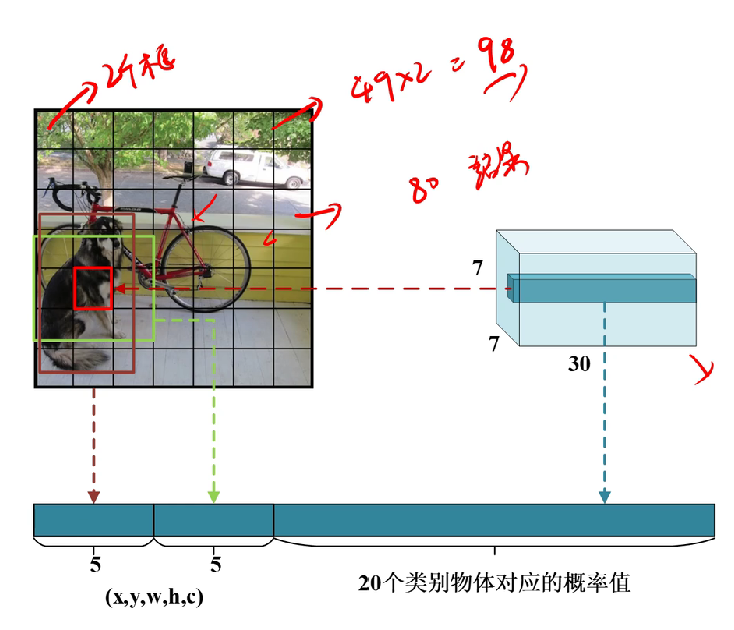
对获取的（x,y,w,h）的理解，以及怎么运用的

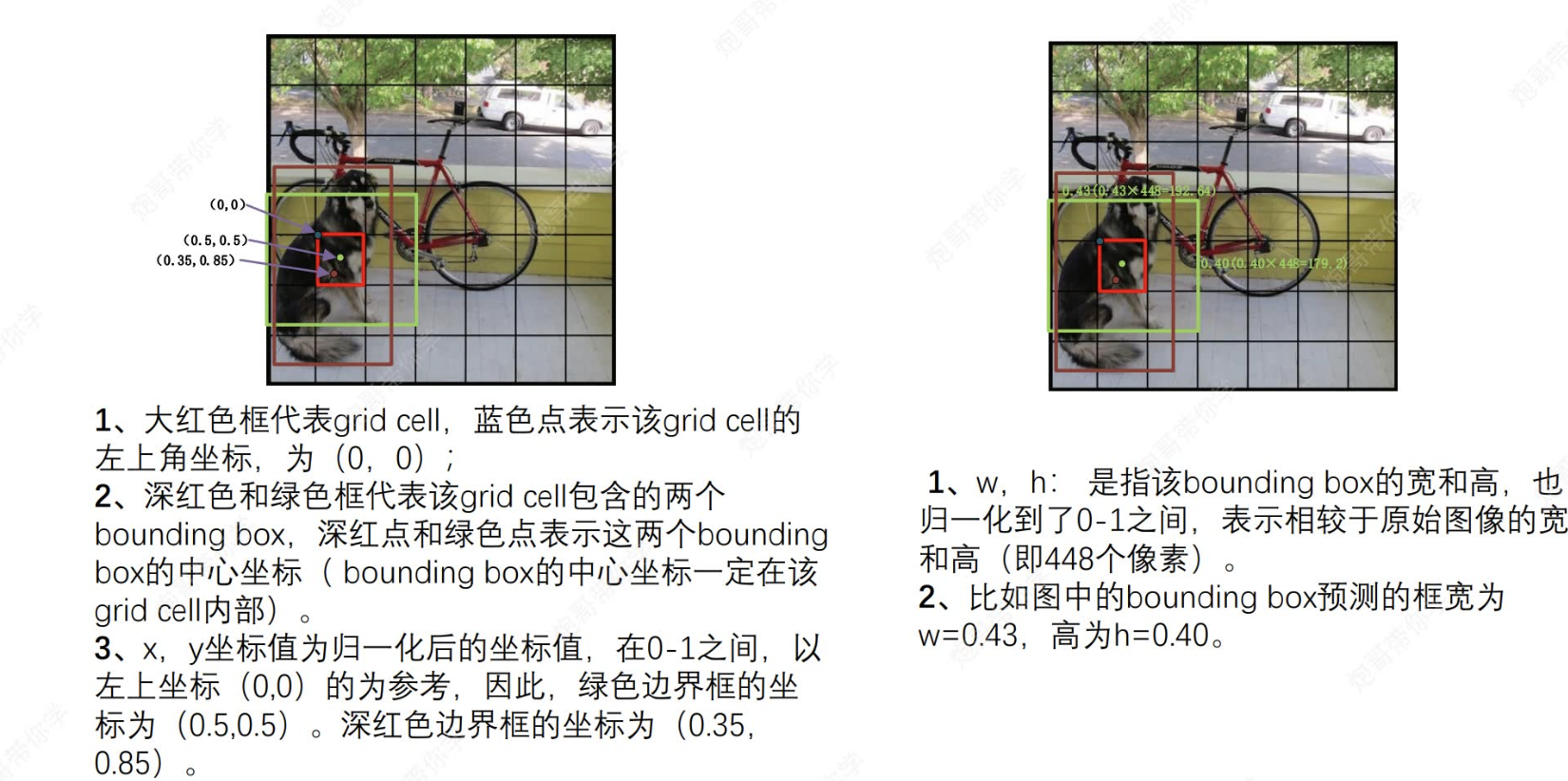
上文我们说到，没过小格子都会得到x,y和w,h信息。接下来将解读这些信息：
（1）每个小格子都以自身左上角顶点为（0,0）原点，每个小个子所获取的两个预测框的中心一定在格子里面，并且坐标值都是经过归一化标注于在各自原点的坐标系之中，然后映射到原图坐标：
eg:绿色边框的中心坐标为（0.5,0.5）,格子有49个，原图为448*448像素，则每个格子为64个像素，则该绿色中心在原图的映射y坐标为0.5*64+64*4.

（2）而对于w,h，其值也是进行了归一化，映射为原始图像的宽高（这里也是每个格子都拥有全局信息的证明，能获取全局信息）。

eg: w=0.43,h=0.40那么原始图像的宽高就是448*0.43；448*0.40。

好啦好啦，不学了，还有没讲完的，精彩请看下一集~~