决策树

前言

参考了大佬的博客：博客地址

适合分析离散数据，若是连续数据需要转换成离散数据再做分析(比如图中的年龄)

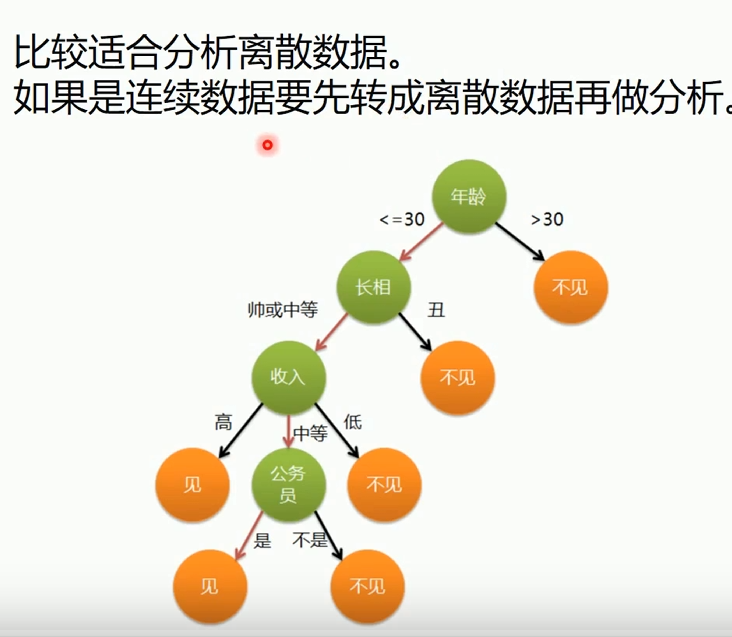
结构

决策树由节点和有向边组成；节点可分为内部节点和叶节点

• 内部节点:特征
• 叶节点:类别
• 有向边:特征的取值范围

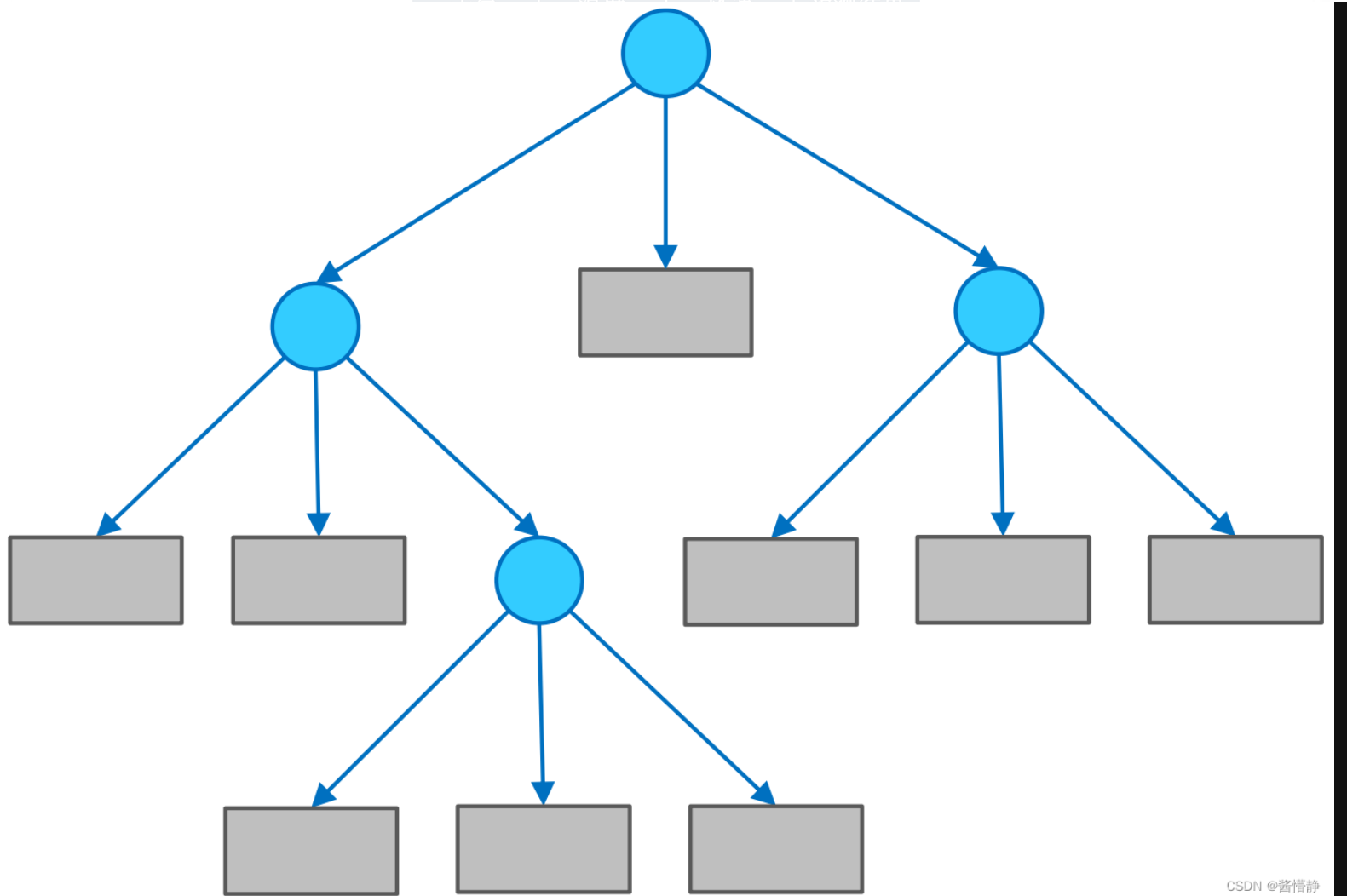
在用决策树进行分类时，首先从根结点出发，对实例在该结点的对应属性进行测试，接着会根据测试结果，将实例分配到其子结点；然后，在子结点继续执行这一流程，如此递归地对实例进行测试并分配，直至到达叶结点；最终，该实例将被分类到叶结点所指示的结果中

在决策树中，若把每个内部结点视为一个条件，每对结点之间的有向边视为一个选项，则从根结点到叶结点的每一条路径都可以看做是一个规则，而叶结点则对应着在指定规则下的结论。这样的规则具有互斥性和完备性，从根结点到叶结点的每一条路径代表了一类实例，并且这个实例只能在这条路径上。从这个角度来看，决策树相当于是一个 if-then 的规则集合，因此它具有非常好的可解释性

熵

作用

表示随机变量的不确定度；对于决策树的节点来说，理想状态是节点特征对样本进行分类后，能最大程度降低样本的熵;可以这样理解，构建决策树就是对特征进行层次选取，而衡量特征选取的合理指标，就是熵

定义

$$\begin{gathered} 对于在有限范围内的离散随机变量X,概率分布为: \\ P(X=x_i)=p_i,i=1,2,\dots ,n \end{gathered}$$

我们假设一个样本中有k个类别，比如不同颜色的球

$$\begin{gathered} k=4 \\ {p}_{blue}=\frac{2}{7},p_{yellow}=\frac{2}{7},p_{red}=\frac{2}{7},p_{green}=\frac{1}{7} \end{gathered}$$
则离散随机变量X的熵定义为
$$\begin{gathered} H(X)=-\sum _{i=1}^k{p}_{i}log{p}_i=-\sum _{i=1}^k\frac{|C_i|}{|D|}log\frac{|C_i|}{|D|} \\ {C}_i表示第i类样本,D表示整个数据集 \end{gathered}$$
则X的熵仅与其分布有关，而与取值无关，H(X)也可以写成H§
$$p_i\in [0,1],log{p}_i\in (-\infty ,0],-log{p}_i\in [0,+\infty )$$
当k很大时，H(X)也会变得很大

条件熵

引入

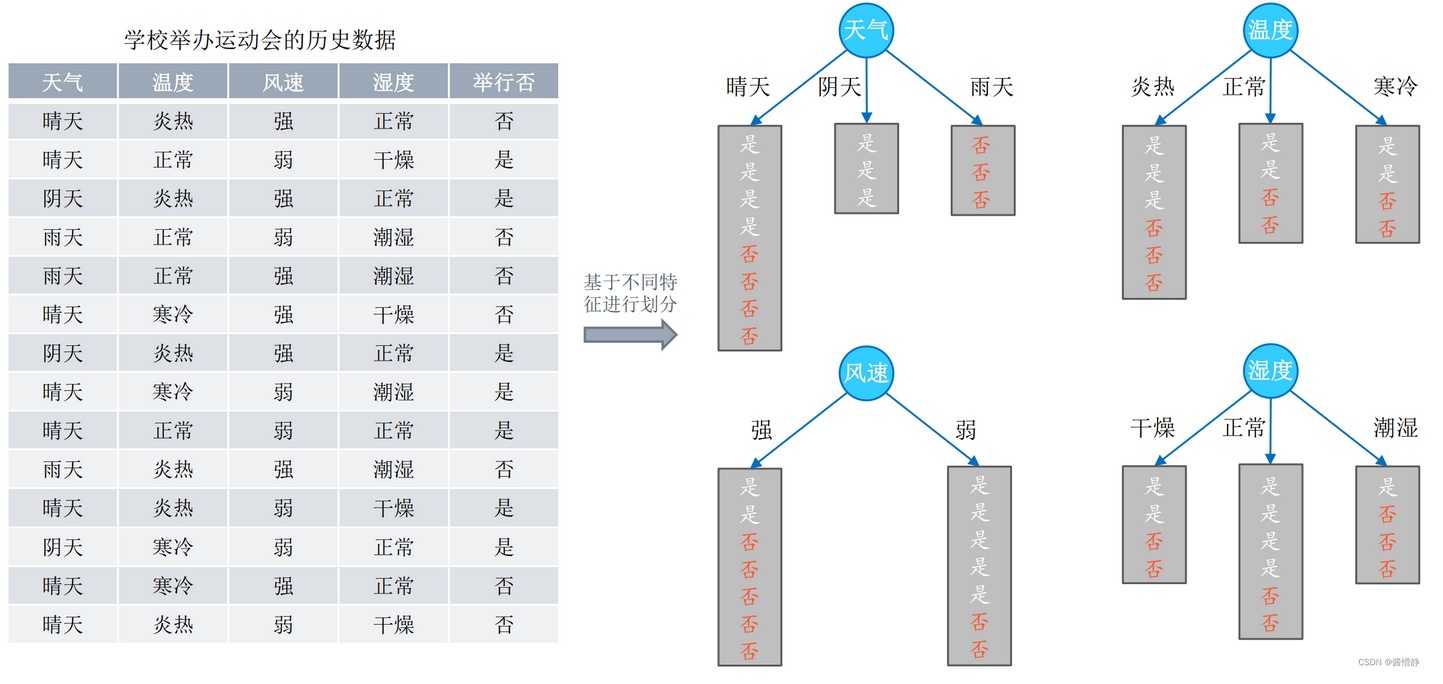
以天气为例，晴天为A类，阴天为B类，雨天为C类；他们都有k=2个类别，即是/否
$$\begin{gathered} H(X_A)=-\sum _{i=1}^2{p}_{i}log{p}_i=-(\frac{1}{2}log\frac{1}{2}+\frac{1}{2}log\frac{1}{2})=log2 \\ H(X_B)=-\sum _{i=1}^2{p}_{i}log{p}_i=-(1log1+log0)=0 \\ H(X_C)=-\sum _{i=1}^2{p}_{i}log{p}_i=-(0log0+1log1)=0 \end{gathered}$$
整体天气系统的熵
$$\begin{gathered} P(X_A)=\frac{8}{14},P(X_B)=\frac{3}{14},P(X_C)=\frac{3}{14} \\ H(X_{天气})=\frac{8}{14}\times H(X_A)+\frac{3}{14}\times H(X_B)+\frac{3}{14}\times H(X_C)=\frac{4}{7}log2 \end{gathered}$$

定义

上面的例子其实就是在求条件熵
$$\begin{gathered} 概率统计中条件概率公式:P(A|B)=\frac{P(AB)}{P(B)} \\ 对于随机变量(X,Y),其联合分布P(X=x_i,Y=y_j)=p_{ij} \end{gathered}$$

$$\begin{gathered} H(Y|X)=\sum _{i=1}^k{p}_{i}H(Y|X=x_i) \\ H(Y|X):在X条件下的熵 \\ {p}_i:P(X=x_i) \end{gathered}$$

划分选择

信息增益

ID3算法选用的评估标准
$$\begin{gathered} g(D,X)=H(D)-H(D|X) \\ H(D|X)=\sum _{i=1}^k\frac{|C_i|}{|D|}H(X=x_i) \\ g(D,X)为信息增益，表示特征X使数据集D不确定性的减少程度 \end{gathered}$$

选择根节点

将使信息增益G(D,X)最大的特征X作为根节点

信息增益率

C4.5算法选用的评估标准

为什么引入信息增益率?

以信息增益作为标准时，会偏向于选择取值较多的特征；比如给定编号与活动是否举办，那么1个编号一定只对应1个是/否，编号必然是最优的特征；但是编号对于类别划分没有帮助，所以我们需要引入一个新的概念-信息增益率
$$\begin{gathered} 信息增益率g_R(D,X)定义为其信息增益g(D,X)与数据集D在特征X上值的熵H_X(D)之比 \\ {H}_X(D)=-\sum _{i=1}^k\frac{|D_i|}{|D|}log\frac{|D_i|}{|D|} \\ |D|:整个数据集样本数,|D_i|:第i类的样本数 \\ {g}_R(D,X)=\frac{g(D,X)}{H_X(D)} \end{gathered}$$

为什么信息增益率能降低偏向于选择取值较多的特征的影响？

当样本数量|D|增加后，|Di|/|D|降低，取对数再取负以后，H_X(D)就增大，信息增益率就降低

基尼系数

CART算法选用的评估标准

基尼系数代表了模型的不纯度，基尼系数越小，则不纯度越低，特征越好

在分类问题中，假设有k个类别，第i个类别概率为pi，则基尼系数为
$$Gini(p)=\sum _{i=1}^k{p}_i(1-p_i)=\sum _{i=1}^k{p}_i-\sum _{i=1}^k{p}_i^2=1-\sum _{i=1}^k{p}_i^2$$
对于数据集D，假设有k个类别，第i个类别的数量为C_i,则数据集D的基尼系数为
$$Gini(D)=\sum _{i=1}^k\frac{|C_i|}{|D|}(1-\frac{|C_i|}{|D|})=1-\sum _{i=1}^k(\frac{|C_i|}{|D|}{)}^2$$
基尼系数其实表示了一个数据集中分类错误的平均概率
$$\begin{gathered} 如果数据集根据X的取值分为D_1,D_2,\dots ,D_k \\ Gini(D,X)=\sum _{i=1}^k\frac{|C_i|}{|D|}Gini(D_i) \\ Gini(D,X)表示数据集D根据特征X划分后的不确定性 \end{gathered}$$
观察公式，其实可以发现面对编号特征时，基尼系数Gini(D,X)会是0

基尼增益

和信息增益类似
$$G(D,X)=Gini(D)-Gini(D,X)$$
采用越好的特征进行划分，得到的基尼增益也越大

基尼仍会认为编号是一个比较优的特征(面对编号特征时，基尼系数Gini(D,X)会是0)

基尼增益率

$$\begin{gathered} 基尼增益率G_R(D,X)可以表示为G(D,X)与数据集D在特征X上的取值个数之比 \\ {G}_R(D,X)=\frac{G(D,X)}{|D_X|} \end{gathered}$$

处理连续值

$$比如有长度为n的连续数据a_1,a_2,\dots ,a_n$$

对其离散化的步骤:

• 排序

• 再任取相邻点的中位点作为划分点
  $$\begin{gathered} \varphi =\frac{a_i+a_{i+1}}{2},1\le i\le n-1 \\ 一共产生n-1个中位点 \end{gathered}$$

• 对这n-1个中位点划分出的数据集进行计算熵，熵最小的就是最优划分点

剪枝

对于决策树而言，如果不断向下划分直至叶子节点的熵为0，理论上我们区分开了所有的类别。但是这样很容易过拟合(划分太多次相当于太多特征导致模型太复杂)，因此我们需要进行剪枝

剪枝策略：

• 预剪枝:边构建决策树边剪枝
• 后剪枝:决策树构建完之后再剪枝

正则化/预剪枝

预剪枝策略可以通过限制决策树深度，叶子节点个数，叶子节点含样本数以及信息增量完成

• 限制决策树高度

  

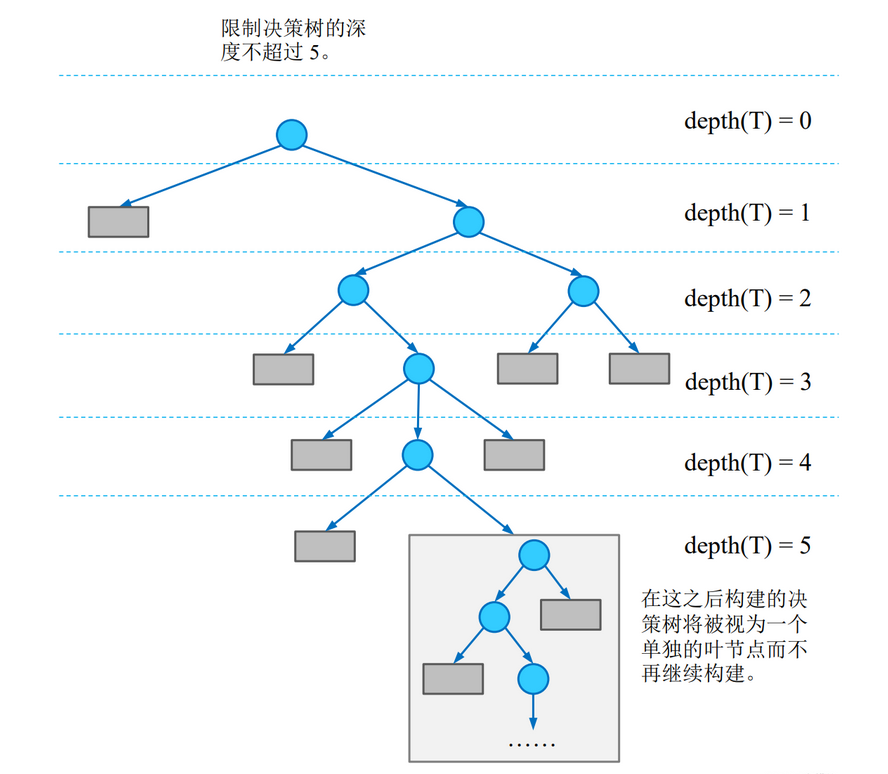
  设定深度限度值d，当深度达到d时，就不再构建决策树(节点不再继续划分数据)，把当前节点作为叶子节点

• 限制叶子节点个数

  

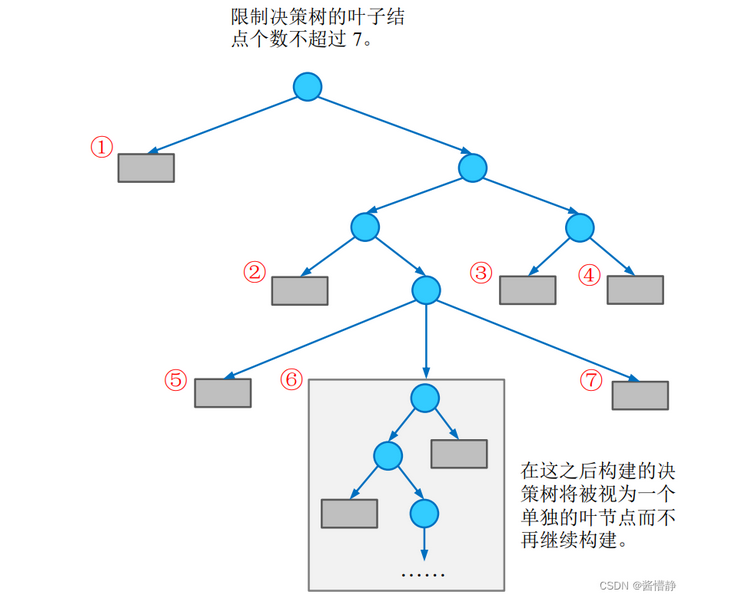
  当达到预设的叶子节点值n时，即使当前节点可以再继续往下划分，也不继续划分了，而是作为叶子节点

• 限制叶子节点样本数

  

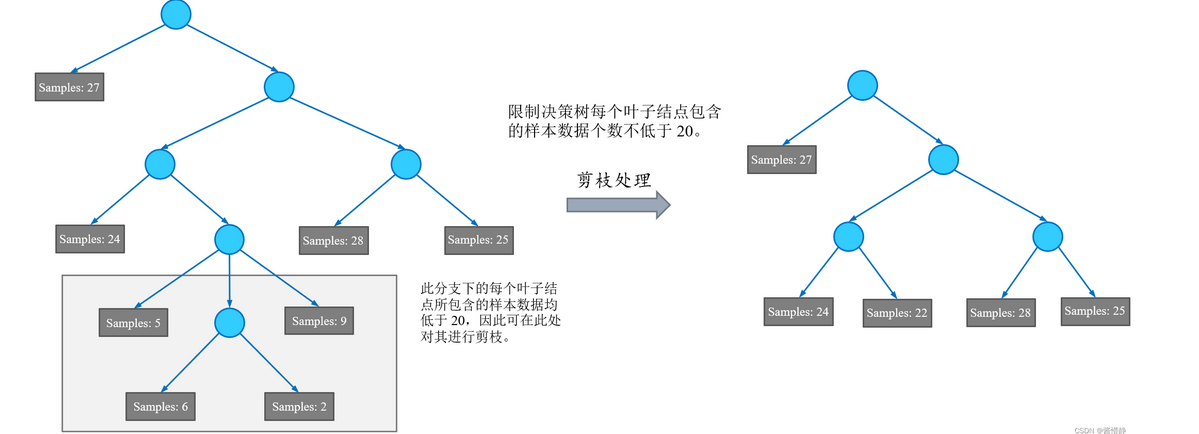
  限制叶子节点的样本数不小于n，如果一个节点下所有分支的叶子节点包含的样本数都小于n，那么需要对这个分支进行剪枝

• 限制最低信息增益

  

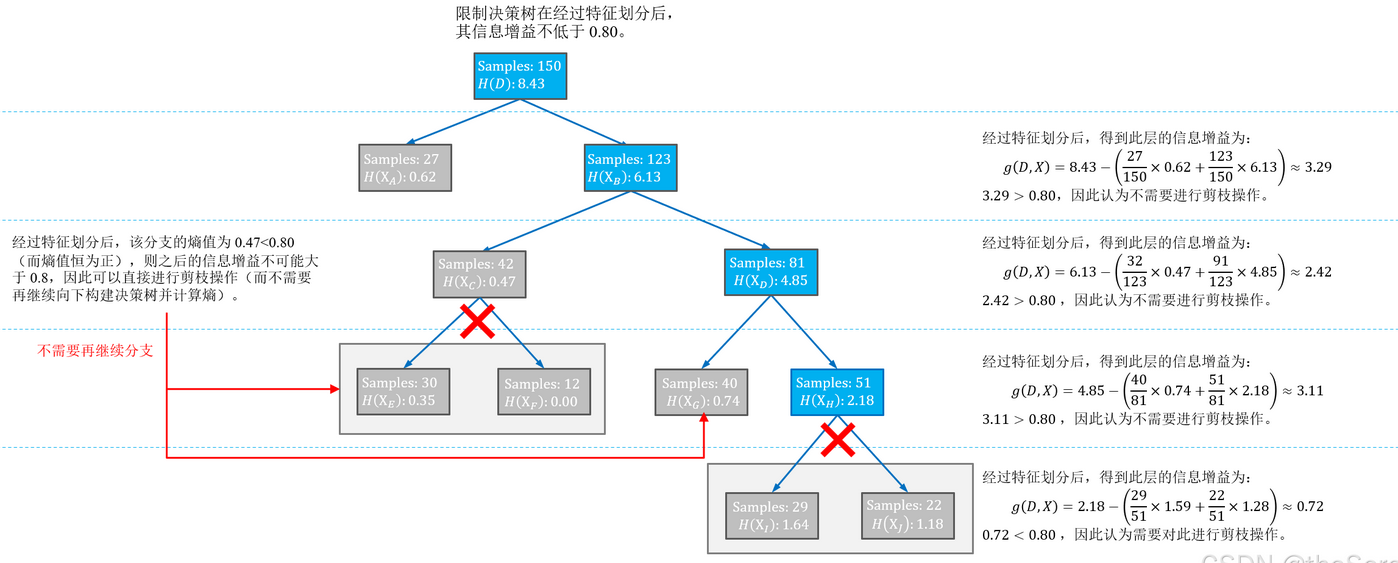
后剪枝

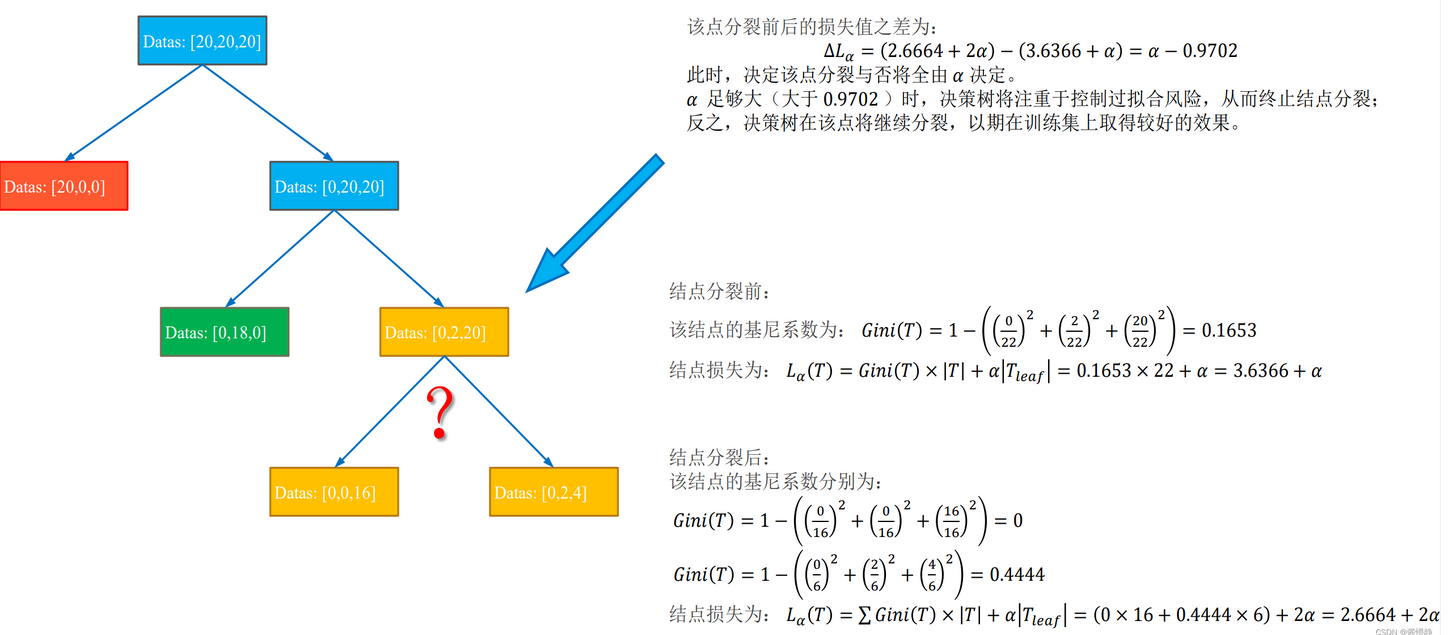
衡量标准
$$\begin{gathered} L_{\alpha }=\sum _{i=1}^n(Gini(T_i)\times |T_i|)+\alpha |T_{leaf}| \\ n是叶子节点数 \\ {L}_{\alpha }表示最终损失(越小越好) \\ Gini(T)表示当前节点的基尼系数 \\ |T|表示当前节点的样本数 \\ {T}_{leaf}表示当前节点被划分后产生的叶子节点个数 \\ \alpha 表示偏好系数，类似于正则化参数\lambda ，越大表示对划分叶子节点惩罚越重 \end{gathered}$$