数字n代表生成括号的对数，请你设计一个函数，用于能够生成所有可能的并且有效的括号组合。

源代码：

class Solution {
public:int n;vector<string> ans;string path;vector<string> generateParenthesis(int n) {this->n = n;dfs(0, 0);return ans;}void dfs(int left, int right) {if (path.size() == 2 * n) {          // 递归出口：已凑够 2n 个字符ans.push_back(path);return;}if (left < n) {                      // 可以加 '('path.push_back('(');dfs(left + 1, right);path.pop_back();                 // 回溯}if (right < left) {                  // 可以加 ')'path.push_back(')');dfs(left, right + 1);path.pop_back();                 // 回溯}}
};

括号的两种关系：排列，嵌套；
讨论第一个括号：
排列：()…
嵌套：(…)
每种情况进行dfs递归；

path设置为string类型，排列的情况只需path = () + path;
嵌套的情况：path = ( + path + )；SB
❌ 嵌套的情况应该是在剩余部分最外侧嵌套，这种写法会导致下次递归会在嵌套外侧修改。

设置前front，待定path，后back三段；
排列的情况：front = front+();
嵌套的情况：front = front+(; back = )+back;

这样只能做到在最前面排列单括号，整体嵌套，整体嵌套中最前面排列单括号，在嵌套中排列单括号；
无法再最后面排列单括号，无法在嵌套括号中排列单括号；

希望随时能直接加()或嵌套；
如果使用了嵌套，则需要在嵌套前，嵌套中，嵌套后的位置同理；
a.嵌套前：
排列：+()；嵌套：在现在的位置后面+(，在最后+）;
b.嵌套中：（前面是本次嵌套的（，后面是本次嵌套的））;
排列：+()；嵌套：在现在的位置后面+(，本次嵌套的)前面+);
c.嵌套后：（前面是上次嵌套的））
排列：+()；嵌套：在现在的位置后面+(，在最后+）；

过于复杂了，这个方法不好。
下面AI给出的实现也报错了：

class Solution {
public:vector<string> generateParenthesis(int n) {vector<string> ans;dfs("", "", n, n, ans);   // prefix, pending, left, rightreturn ans;}private:// 任何时刻真实串 = prefix + pending + 尚未展开的位置void dfs(string prefix, string pending,int left,           // 还能再放几个 '('int right,          // 还能再放几个 ')'vector<string>& ans){// 1. 终止条件：左右括号全都用完if (left == 0 && right == 0) {ans.push_back(prefix + pending);   // pending 此时为空return;}// 2. 在当前“可插入点”直接并列一对 ()//    等价于：prefix + pending + "()"//    注意 left、right 各减 1if (left >= 1 && right >= 1) {dfs(prefix + pending + "()", "", left - 1, right - 1, ans);}// 3. 新开一层嵌套：放一个 '('，并把对应的 ')' 压入 pendingif (left > 0) {dfs(prefix + pending + "(", ")" + pending, left - 1, right, ans);// 注意 pending 被整体右移，相当于把新 ')' 放在本次嵌套的末尾}// 4. 如果还有未匹配的左括号，就把 pending 第一个 ')' 真正落盘if (!pending.empty()) {dfs(prefix + pending[0], pending.substr(1), left, right, ans);// 这里 pending[0] 一定是 ')'}}
};

怎么回退？不回退的话每次递归调用都要定义两个新string。
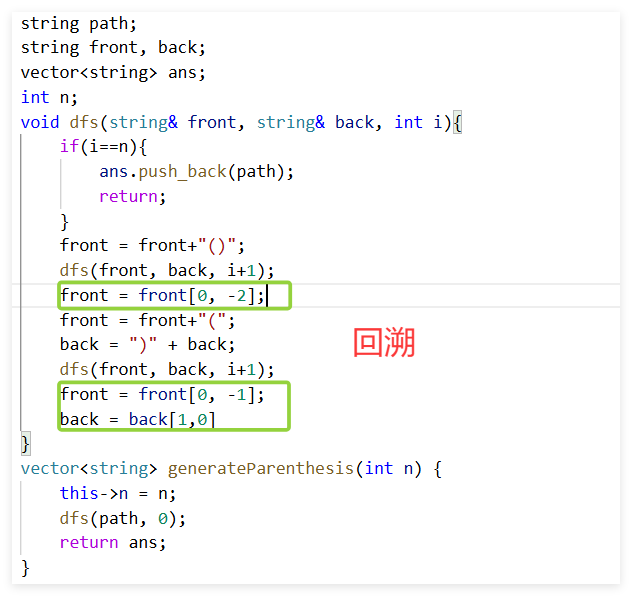
在这里插入图片描述
我是真讨厌string。

string类型的数据常用索引处理，而不直接处理字符串本身。
或者直接将选择过的遍历作为参数传递给递归函数：
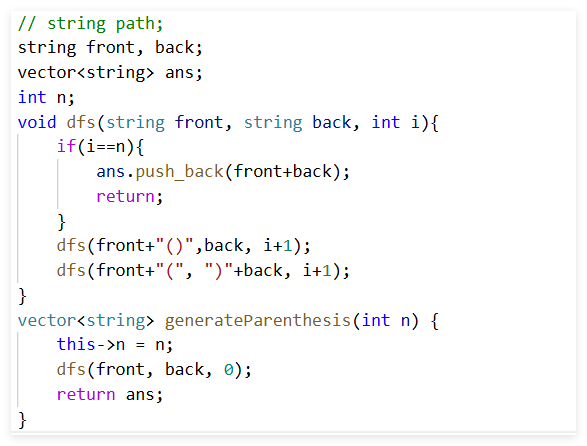
在这里插入图片描述
但是会返回完全一样的两组结果，即重复计算了一次。

n=1
排列: front=(); back=nullptr;
嵌套: front=(; back = );

用无序集去重，再转换成vector：
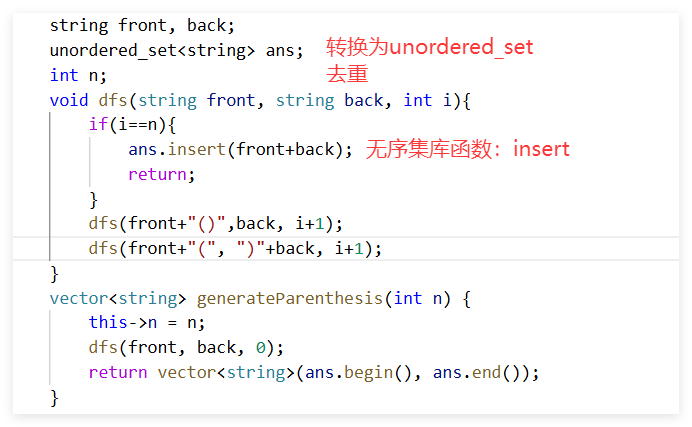
在这里插入图片描述
思路有问题。
无法构造 (())() ；
待定吧，今天懒得想了，再想怕失眠。
无法在最后加()的问题想不到解决的思路。

换思路：感谢灵神
https://leetcode.cn/problems/generate-parentheses/solutions/2071015/hui-su-bu-hui-xie-tao-lu-zai-ci-pythonja-wcdw/?envType=study-plan-v2&envId=top-interview-150

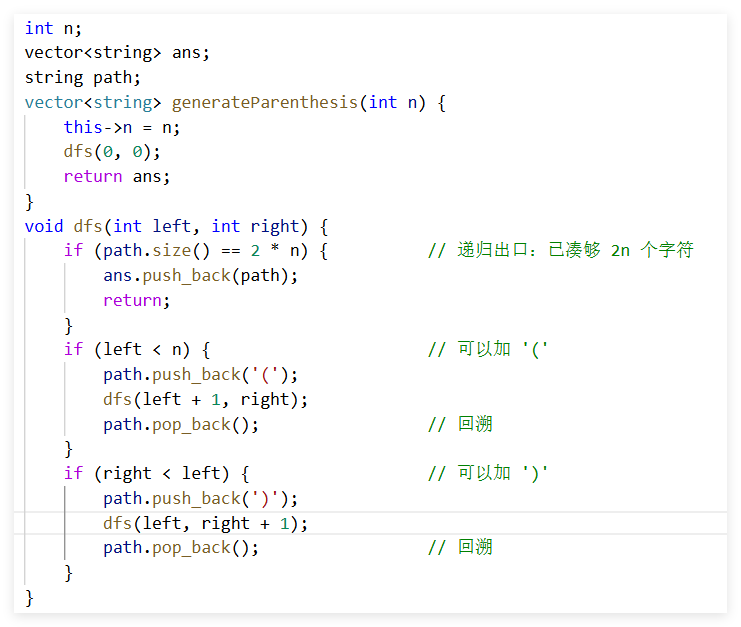
重要条件：当且仅当左括号数量大于右括号数量时，才能加右括号；
有了这个之后直接选与不选子集法；

在这里插入图片描述