一

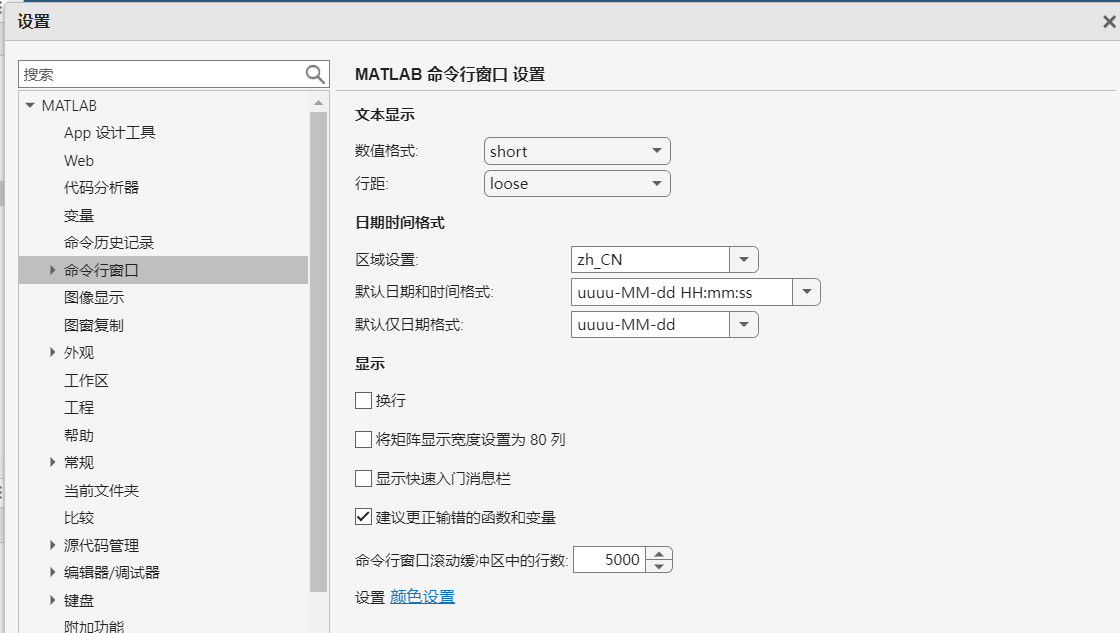
1.数值显示格式

format style 设置

eg: pi format longE;

2.清除指令

clc 清除命令行窗口

clear 清除工作区

cls

3.搜索路径设置

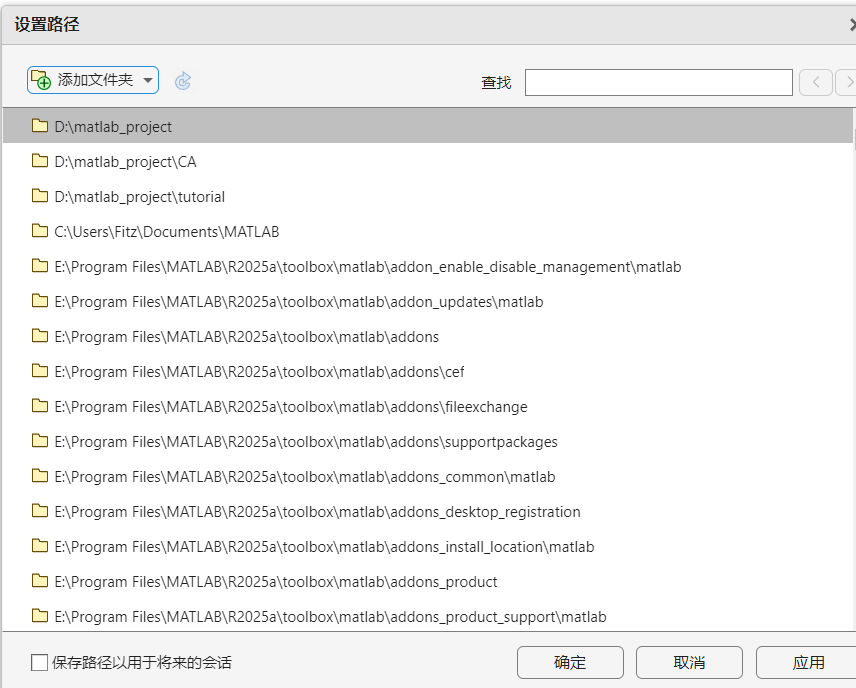
path(path,'E:\ads\')

addpath

4.M文件

用户把要实现的命令写在一个以.m为扩展的文件中，然后由matlab系统进行解读，最后运行结果。

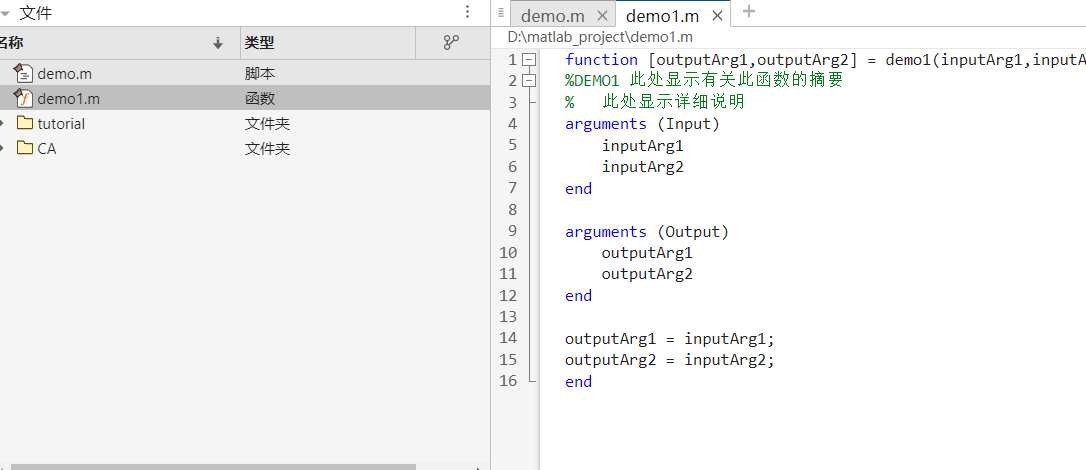
类型：

脚本：也可以自己写函数；

函数：函数名和文件名相同；

5.通用描述

general 命令

函数：rand(), sin(60)

工具箱

abs , sqrt, exp

help abs

分号；，不打印在命令行中

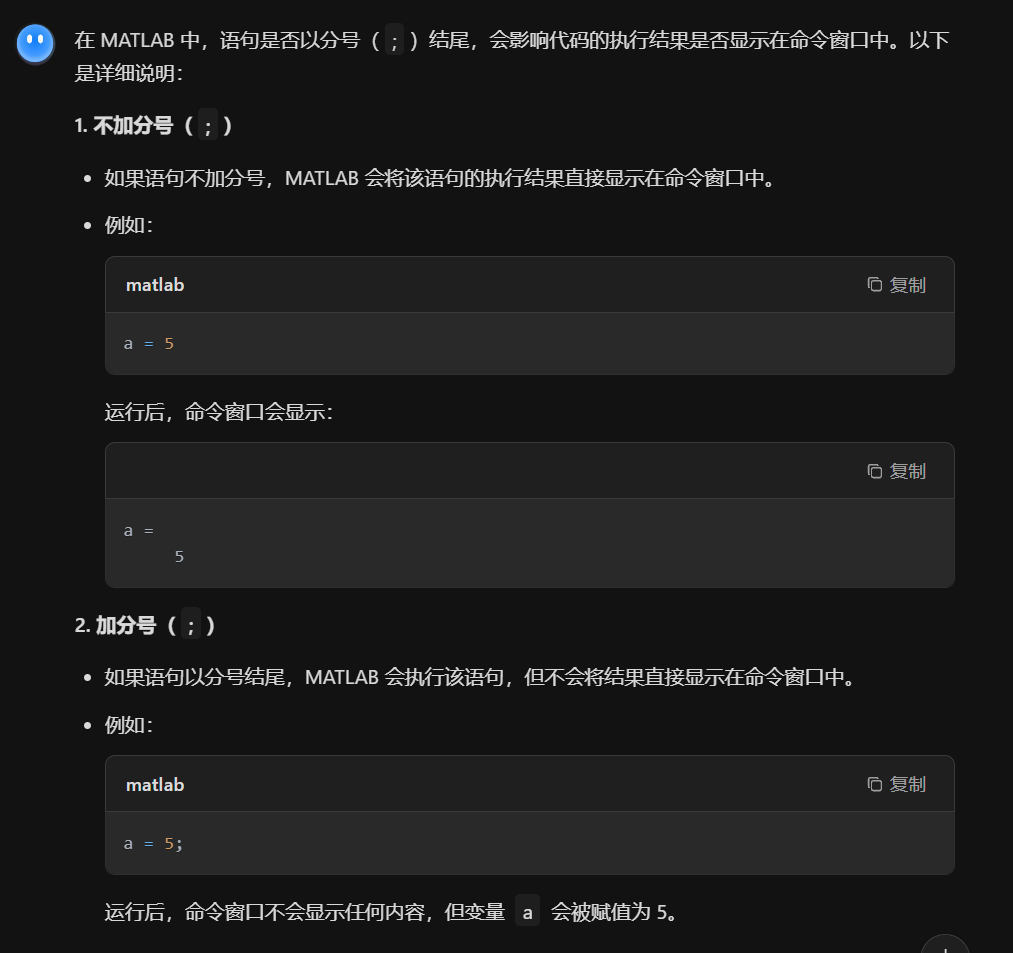
6.通用命令

常用：cls clf clear exit quit home echo type more cd dir load diary pack hold（图形保持

快捷键

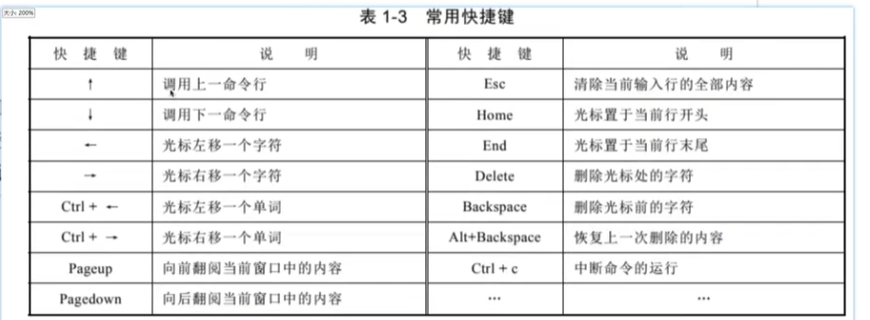
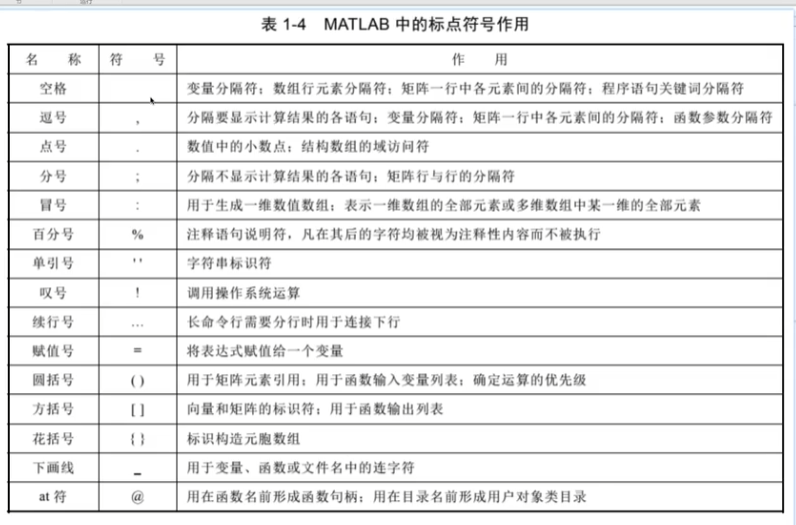
[]向量和矩阵标识符

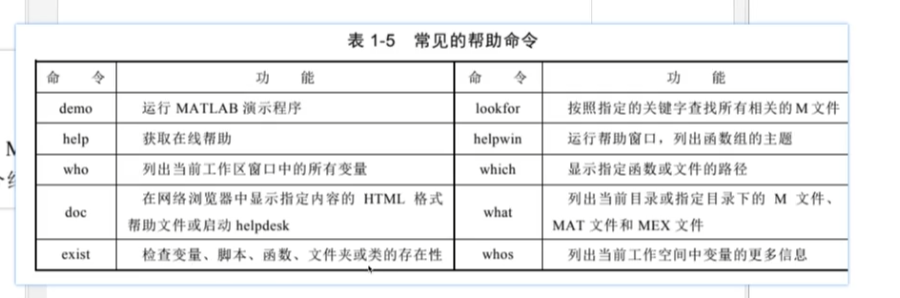
二

1.向量

冒号表示

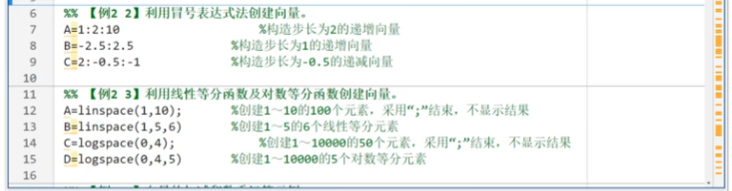
linspace(a1,an,n) n默认100 ，首元素尾元素等分间距

logspace(a1,an,n) n默认50

算数运算

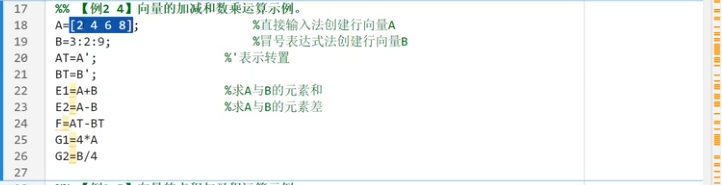
点积和叉积

2.矩阵matrix

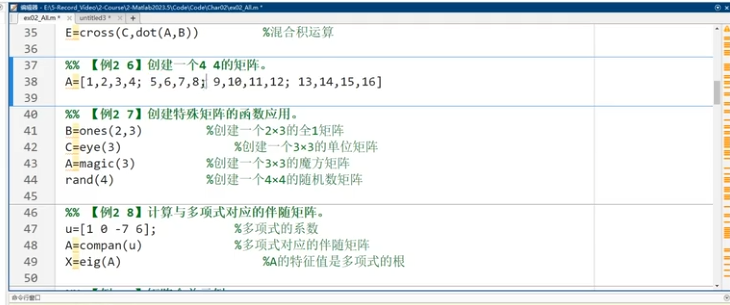
特殊矩阵

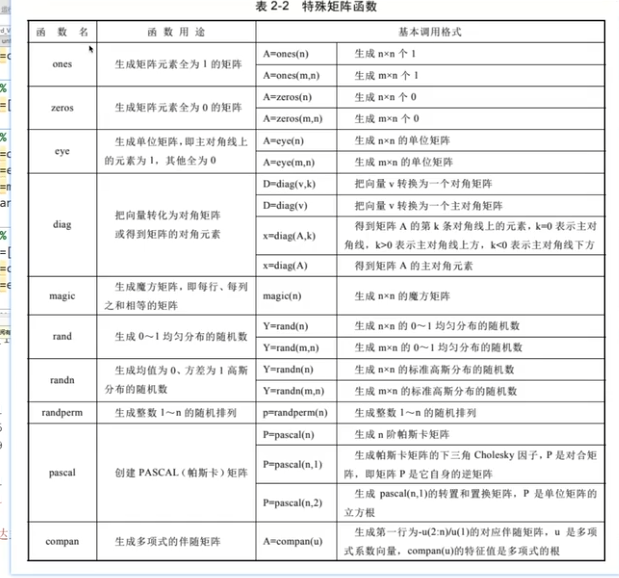
ones(3,3) or ones(3)

zeros( )

eye()

diag()对角

magic

rand 0-1均匀分布

randn 高斯分布

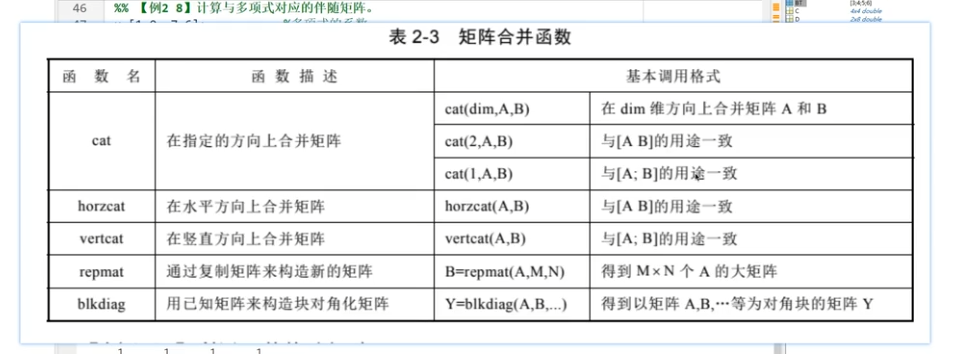
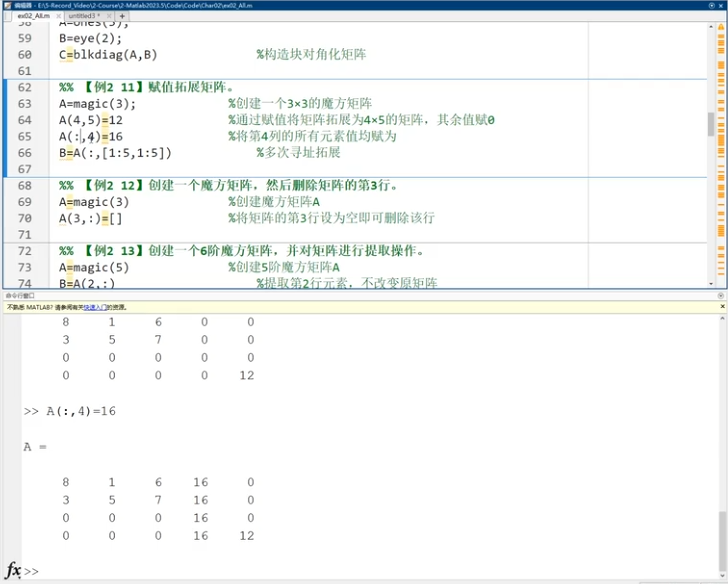
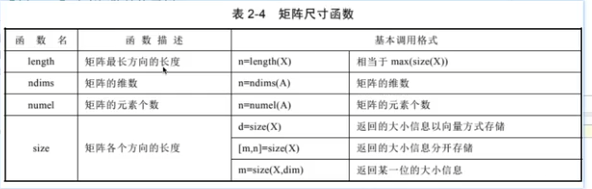
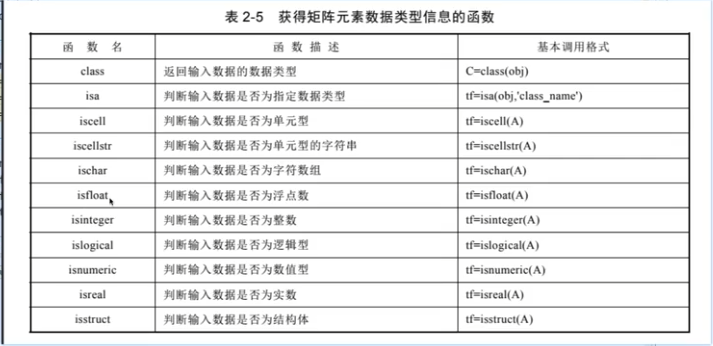
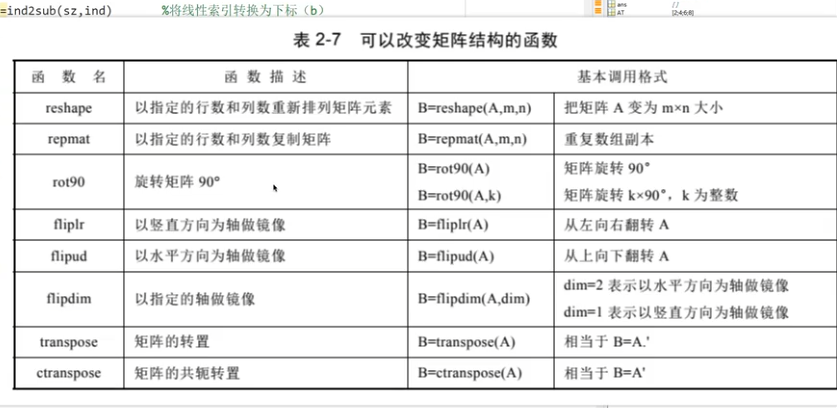
稀疏矩阵

非零元素和行列索引来存，节省空间；

密度：

转换函数：满矩阵-稀疏矩阵

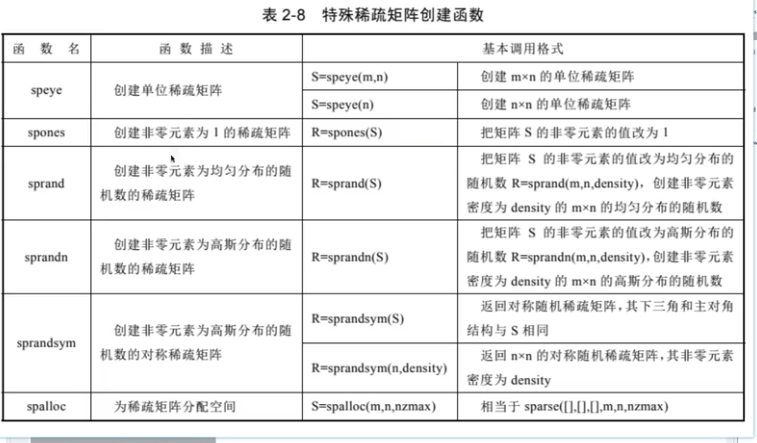
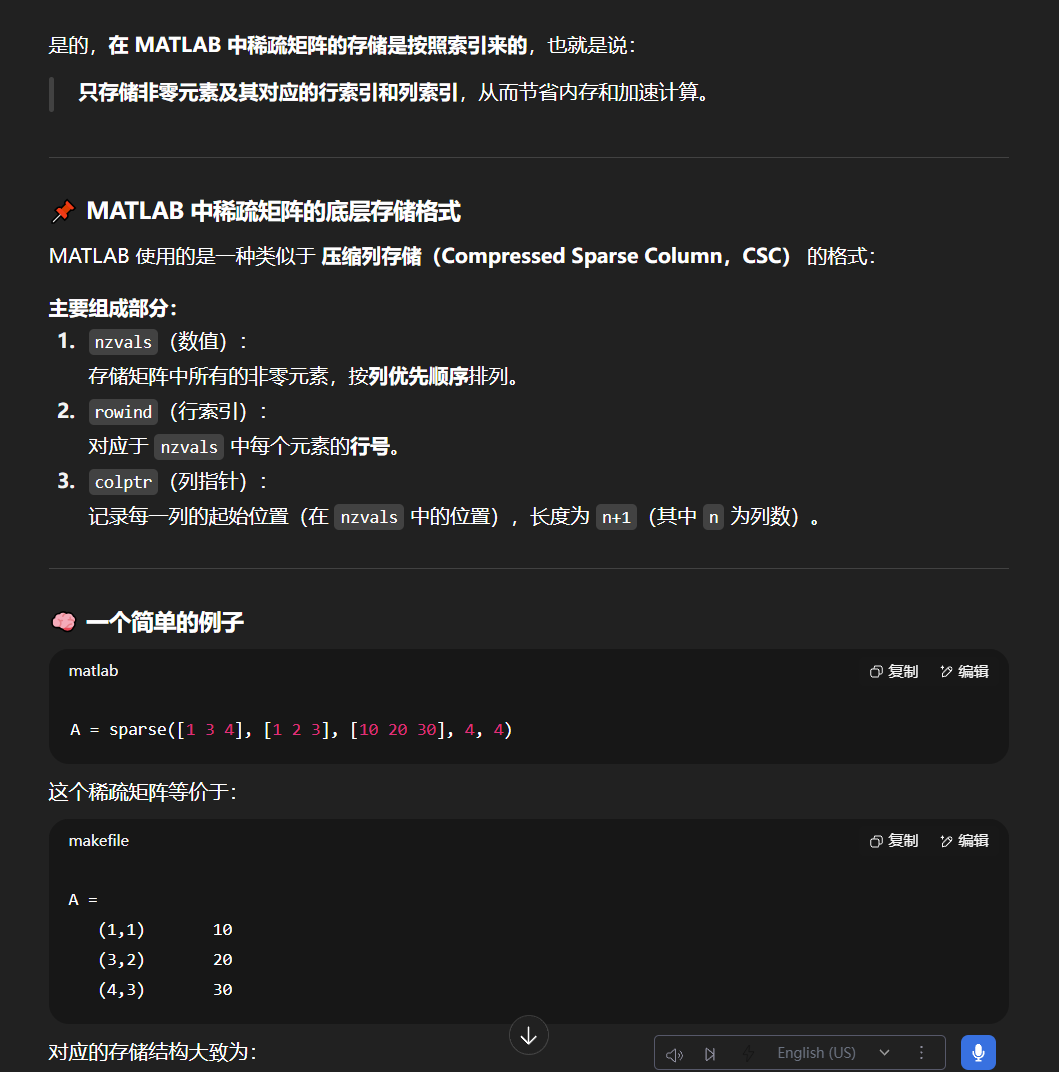
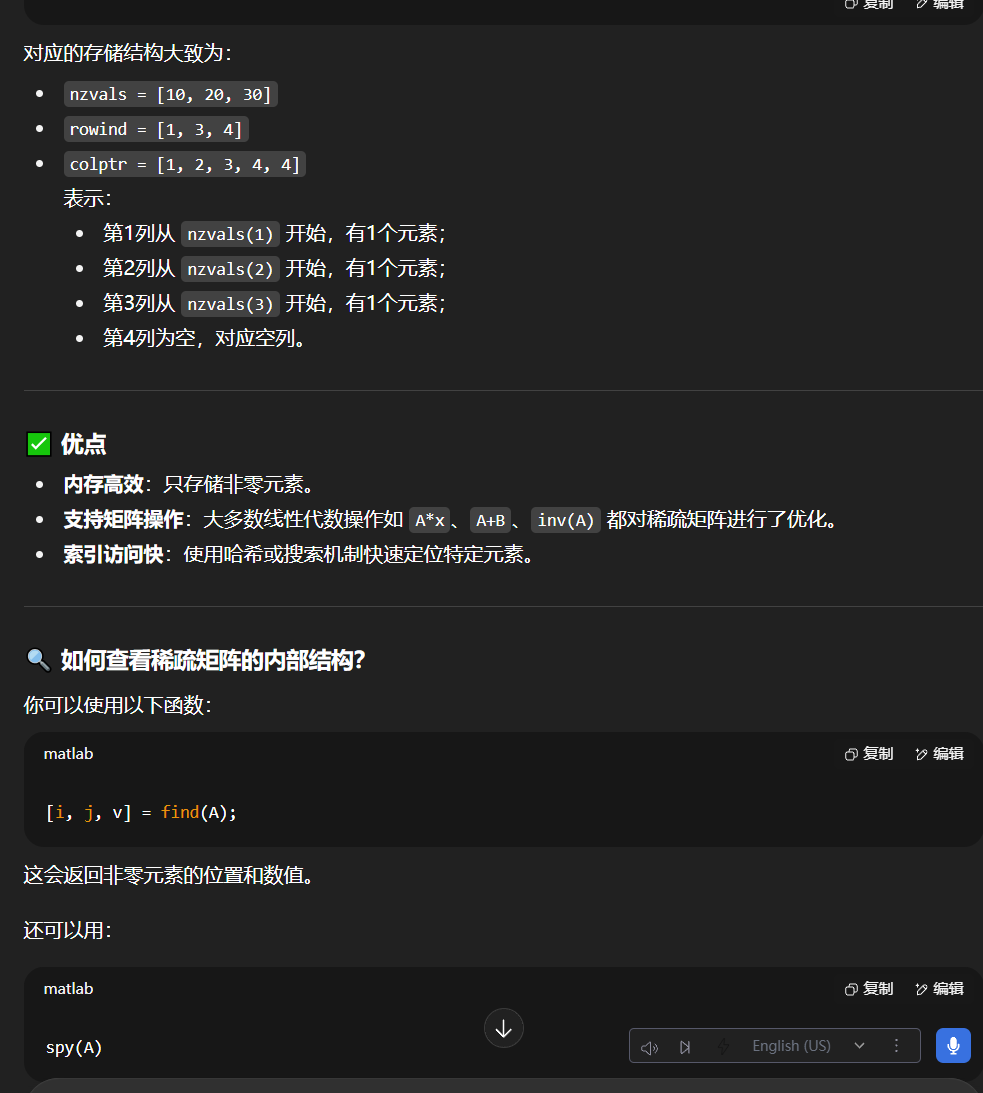
结论

MATLAB 的稀疏矩阵是按索引存储的，采用的是列优先顺序下的压缩列存储（CSC）格式。只保存了非零元素及其所在的行列索引，从而实现了高效的内存利用和运算性能。

导入外部数据 load

多维数组

三

1.数据类型

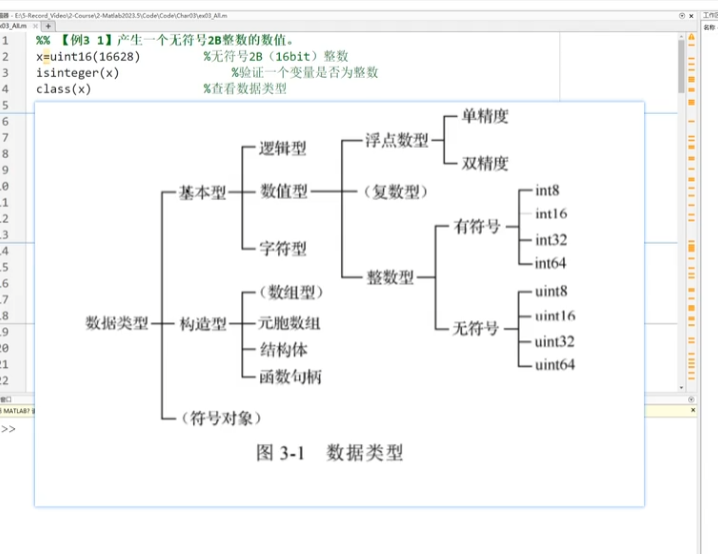
isinteger(x)

class(x)

双精度浮点（默认）

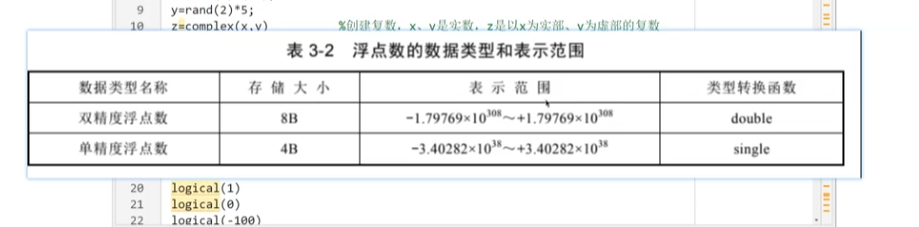
2.类型转换函数

复数：z = complex(x,y)

z = complex(x)

z = 12 + 6i;

z = rand(2)*2

3.字符，结构体（C++）

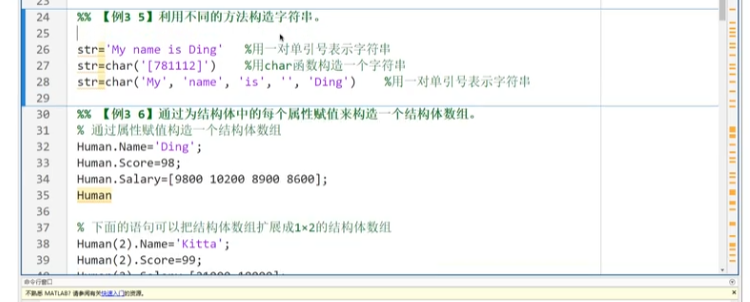
4.元胞数组

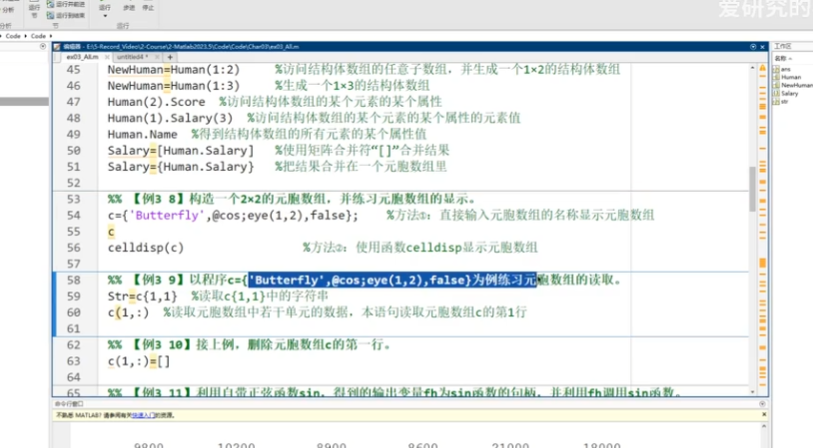
5.函数句柄

可作为参数传递给其他函数，C++中有相同概念函数指针或回调函数，执行时机和逻辑分离；

6.字符串

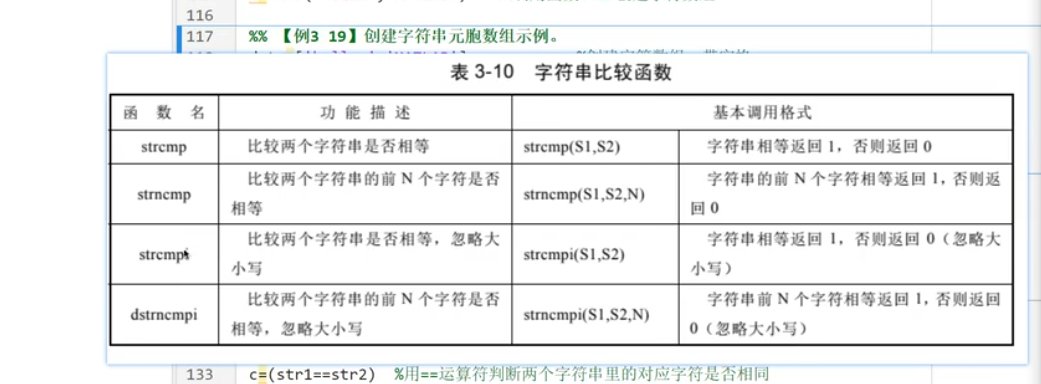
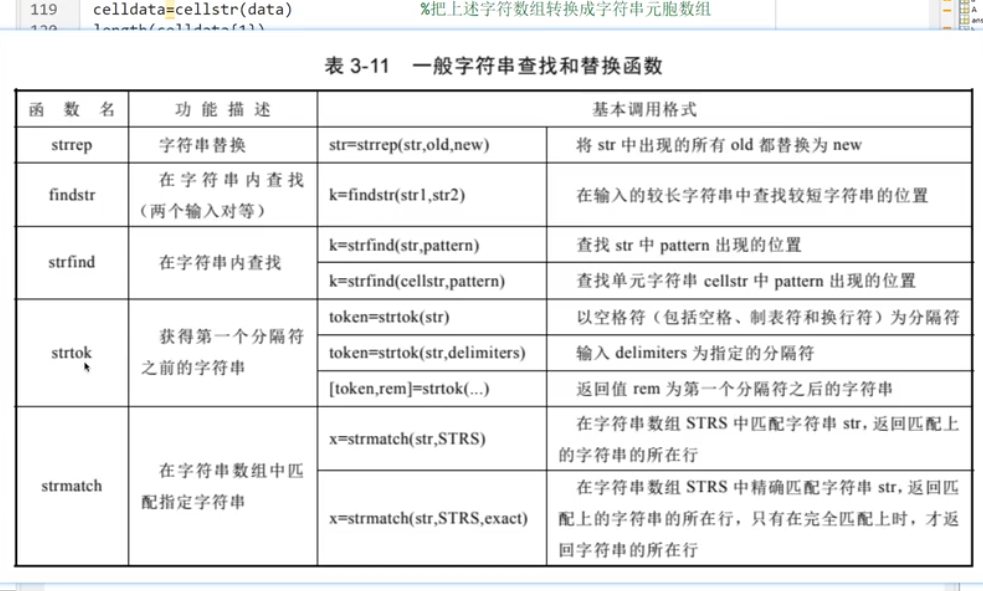
四

1.程序

M文件，扩展名.m。通过编写M文件可以实现各种复杂运算。

eg:

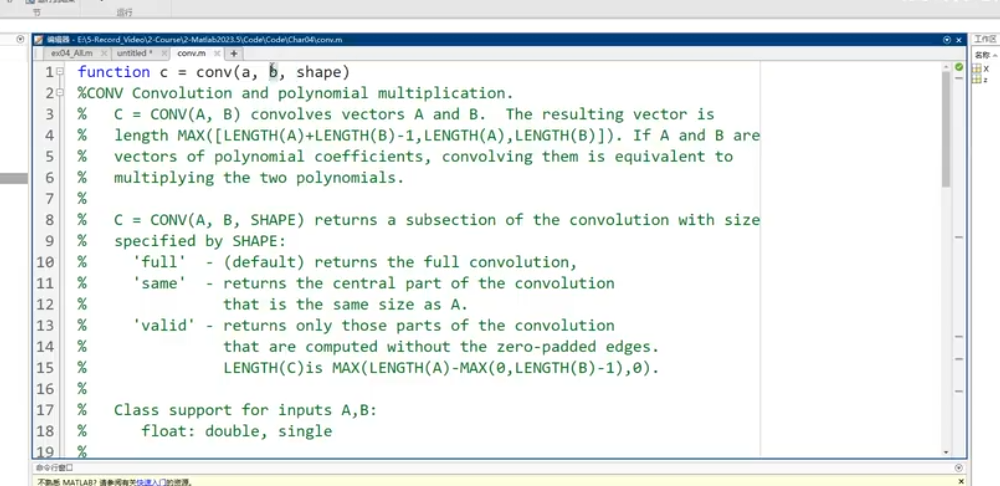
循环语句：for and while 前者有次数，后者没有，通过条件判断式来决定

条件语句：ifelse switch case

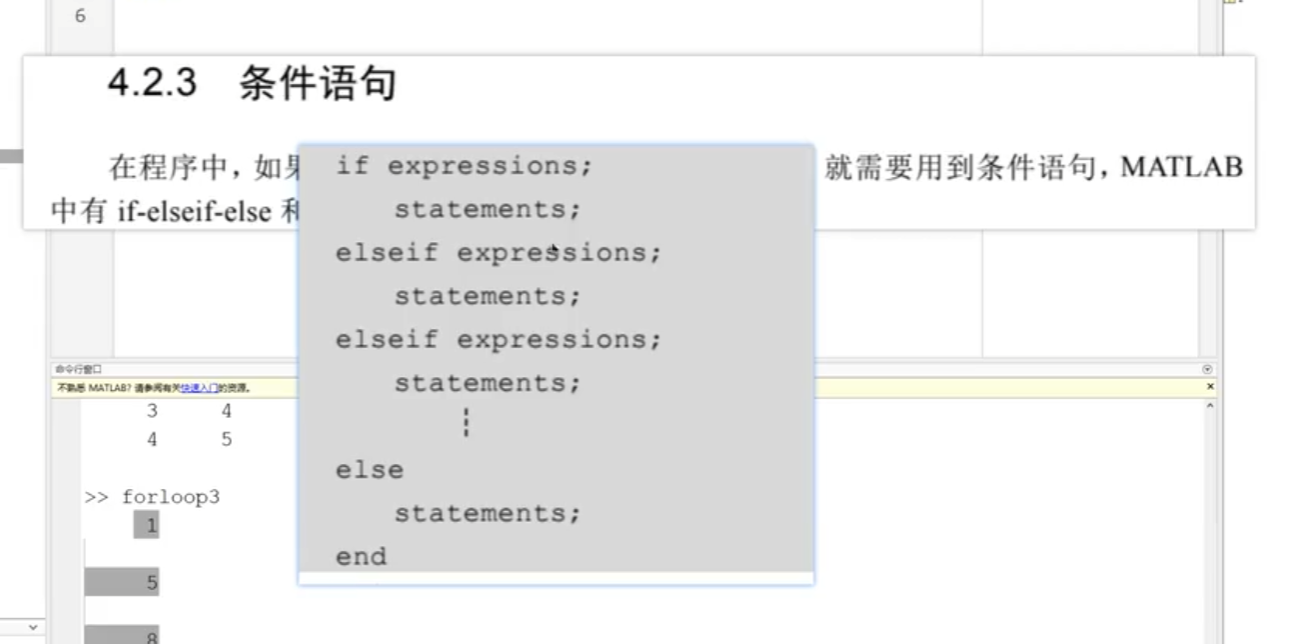
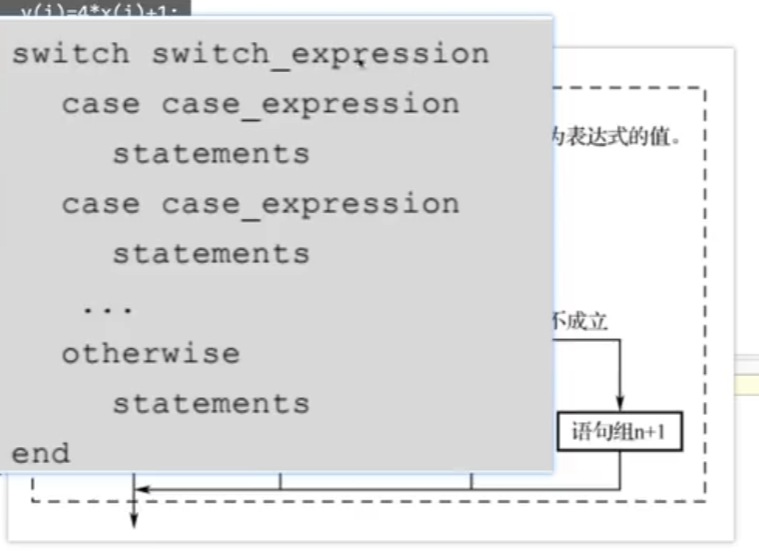
continue

return

break

交互命令：

echo

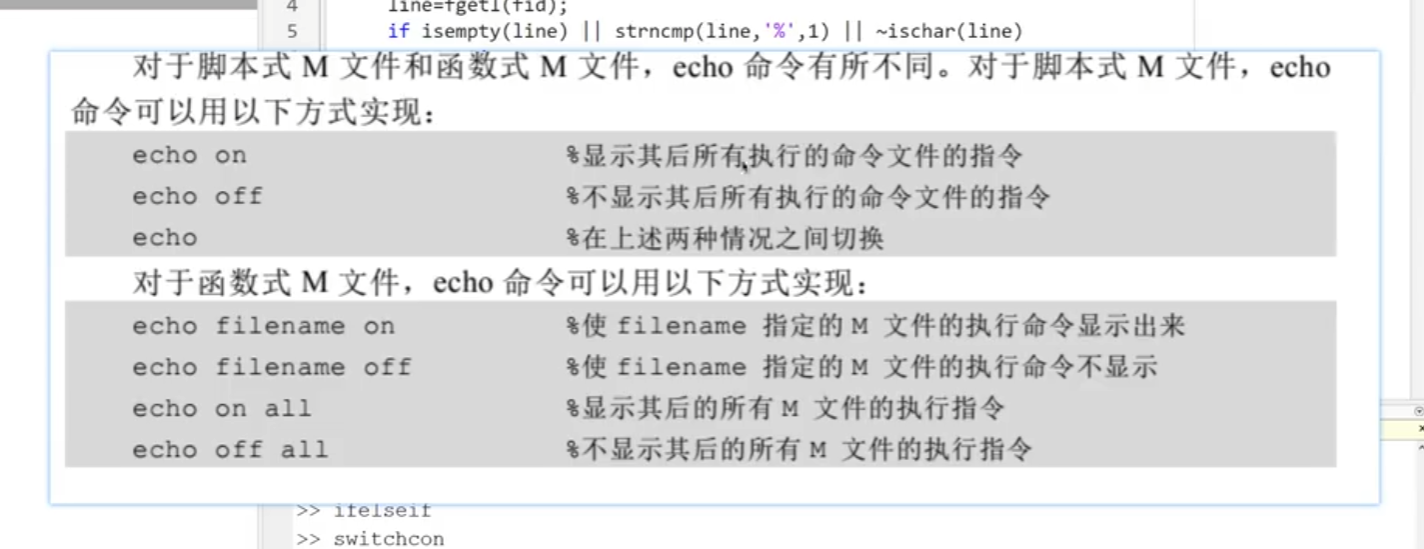error

keyboard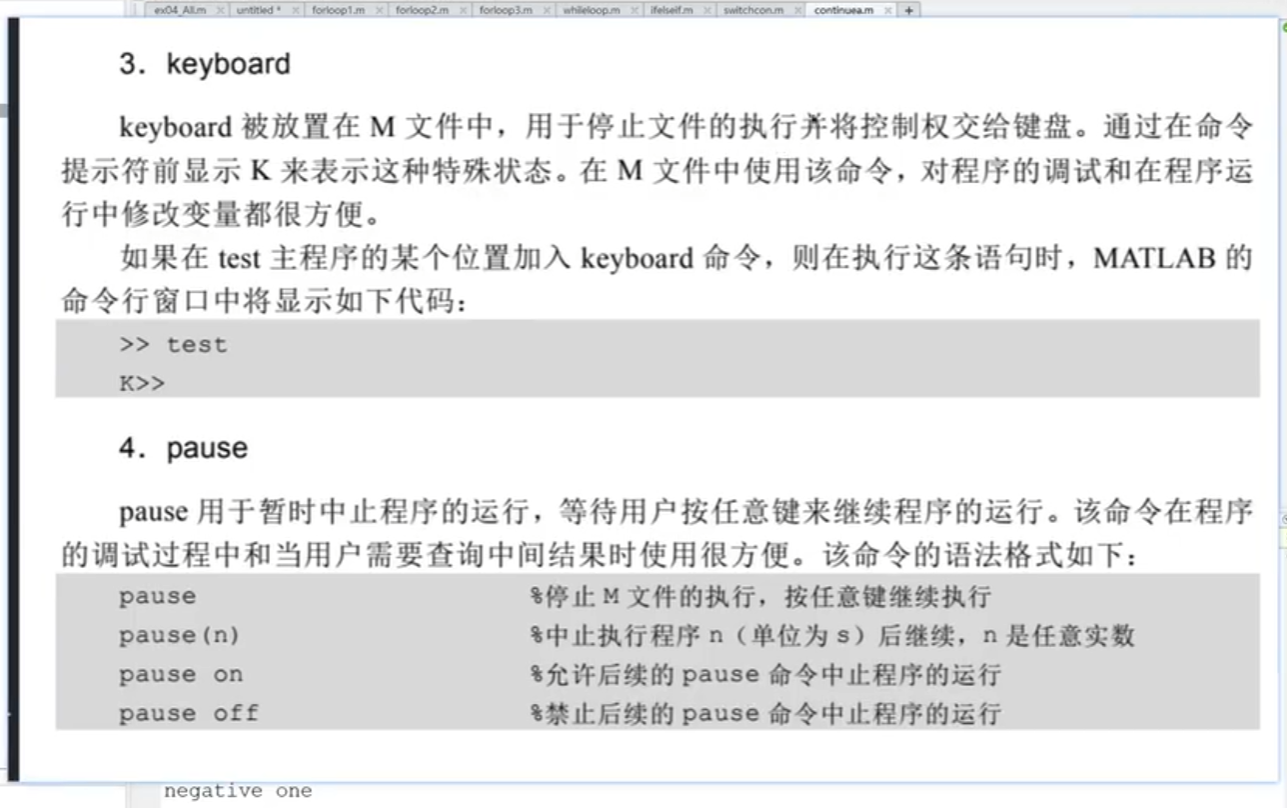

2.调试

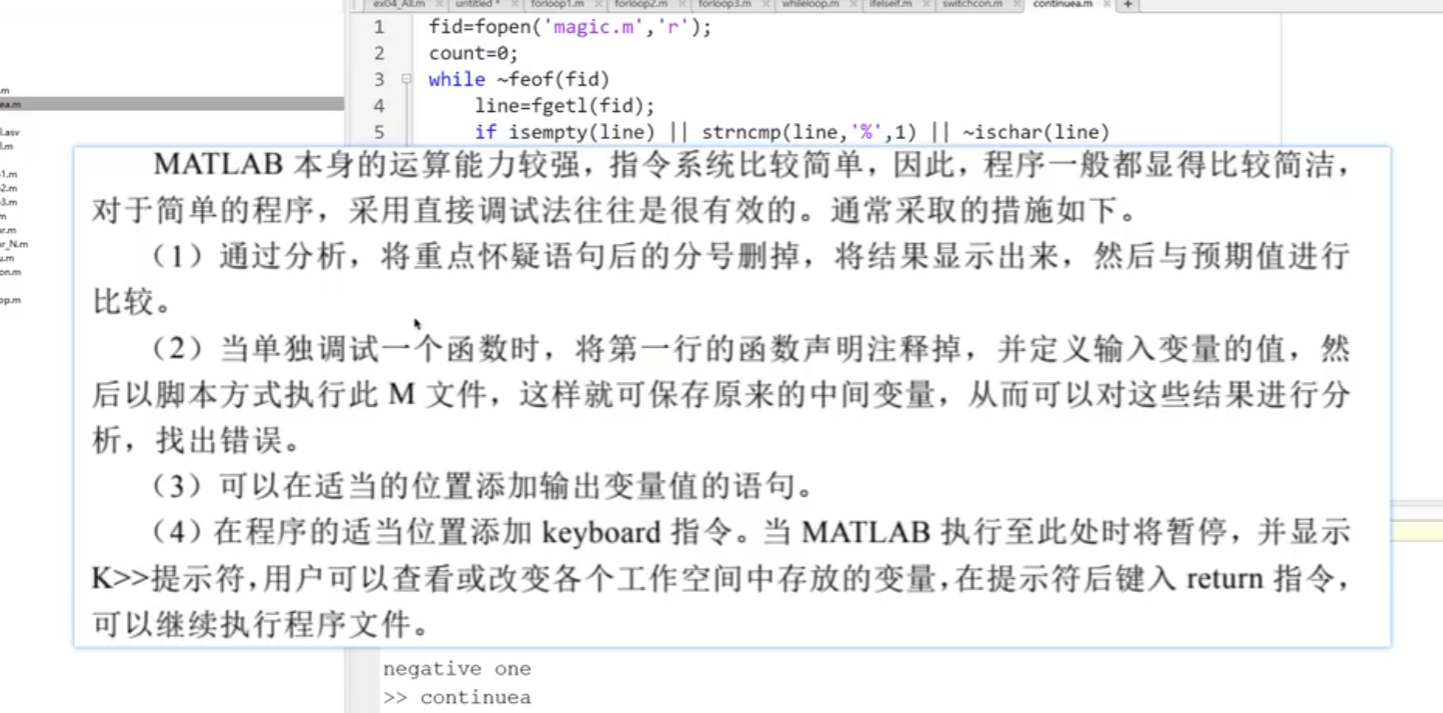
五

矩阵运算

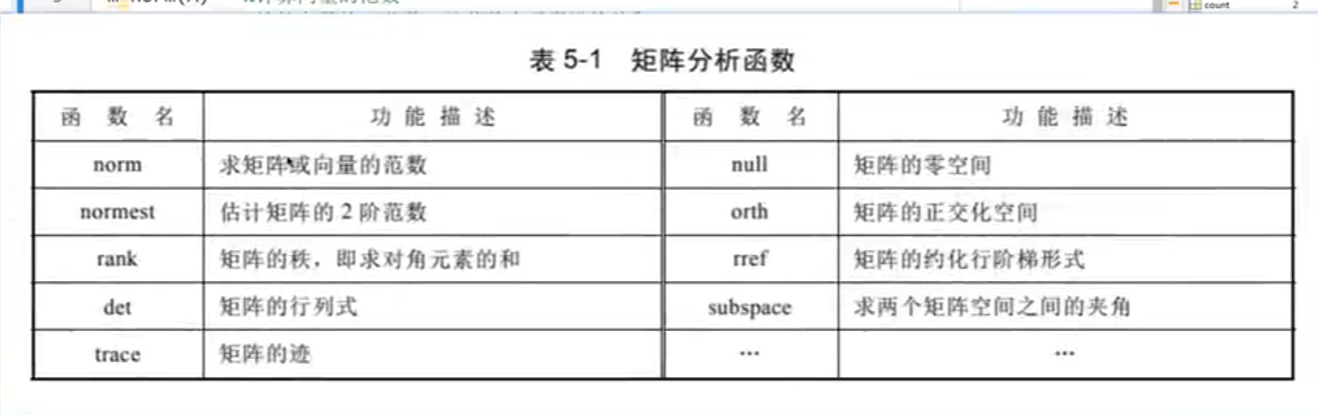
范数

det

cond判断奇异性

rank

trace

特征值和特征向量

矩阵空间夹角

矩阵分解

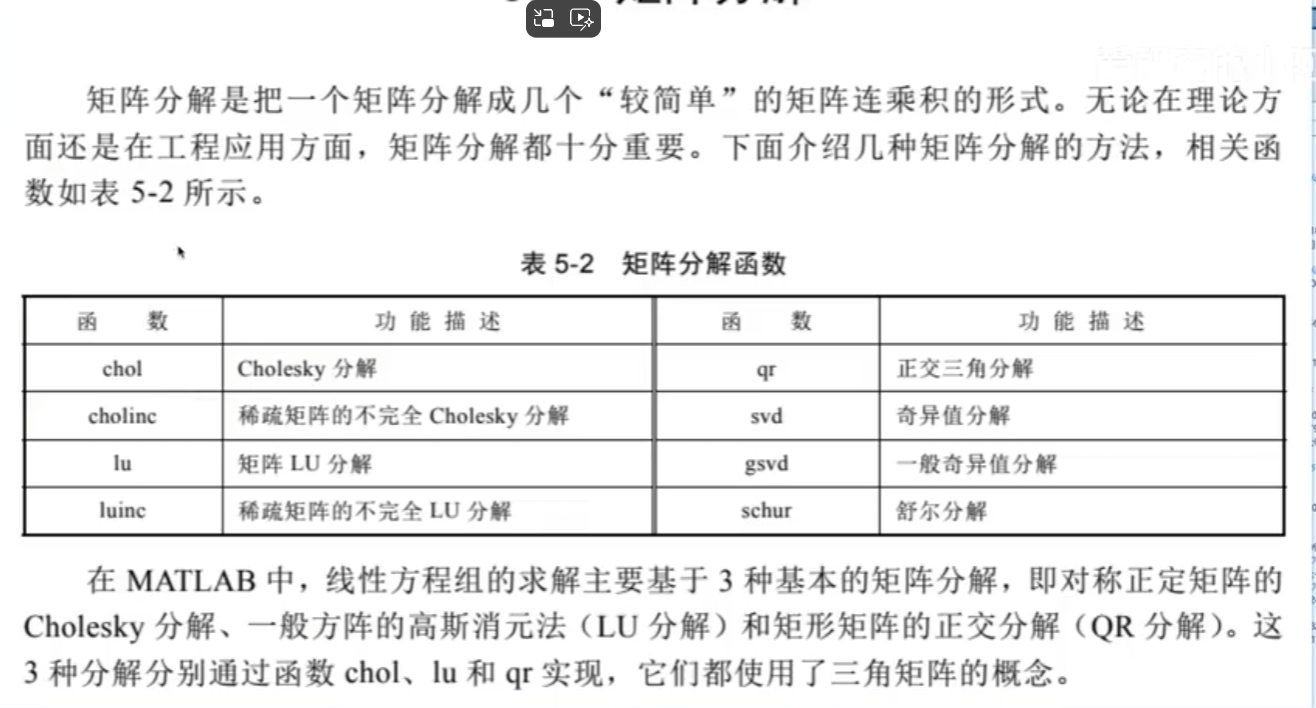
1.chol

2.LU

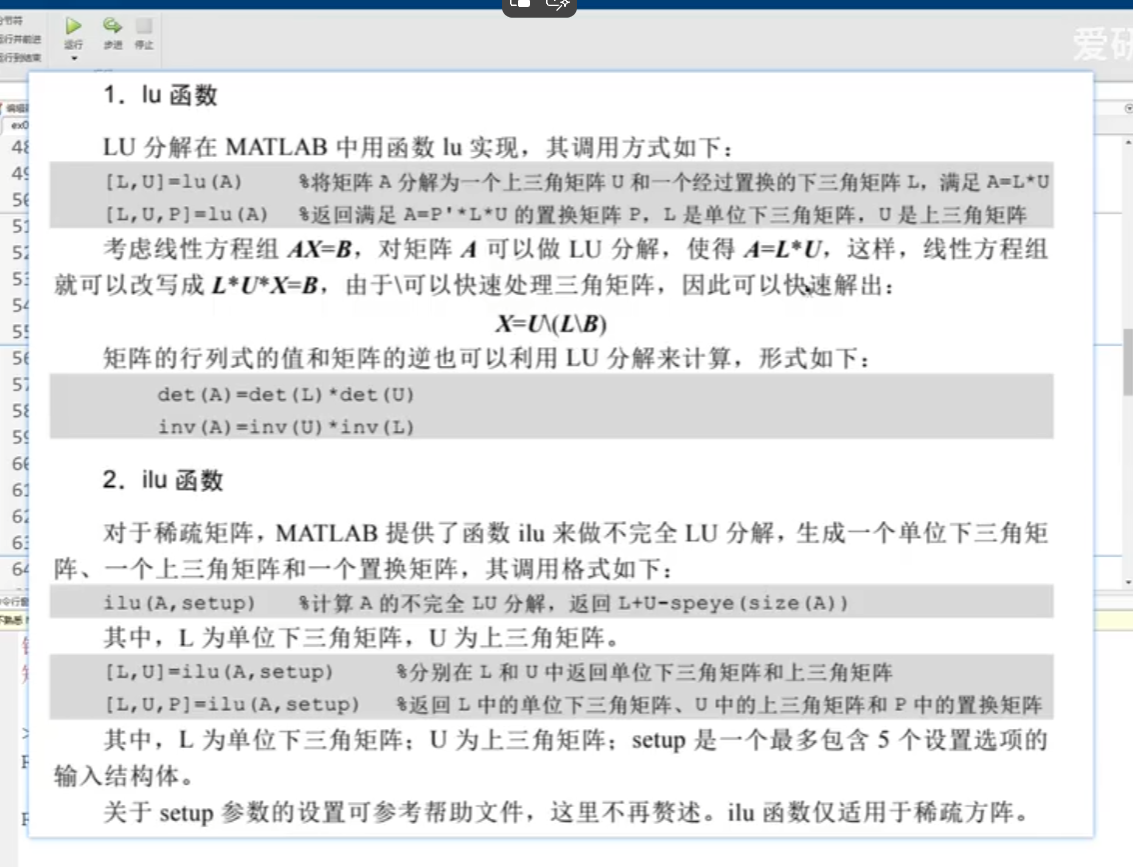
3.QR

4.左右除：

为了方便记忆对哪个矩阵进行逆运算，规律如下：
在可逆形式下转换成逆矩阵，右除对右边矩阵逆，左除对左边矩阵逆。
1. C/B=C*(inv(B)) (C右除B等于C乘以B的逆）
2. A\C=inv(A)*C （A左除C=A的逆乘以C）

六

1.可视化

eg:

步骤：

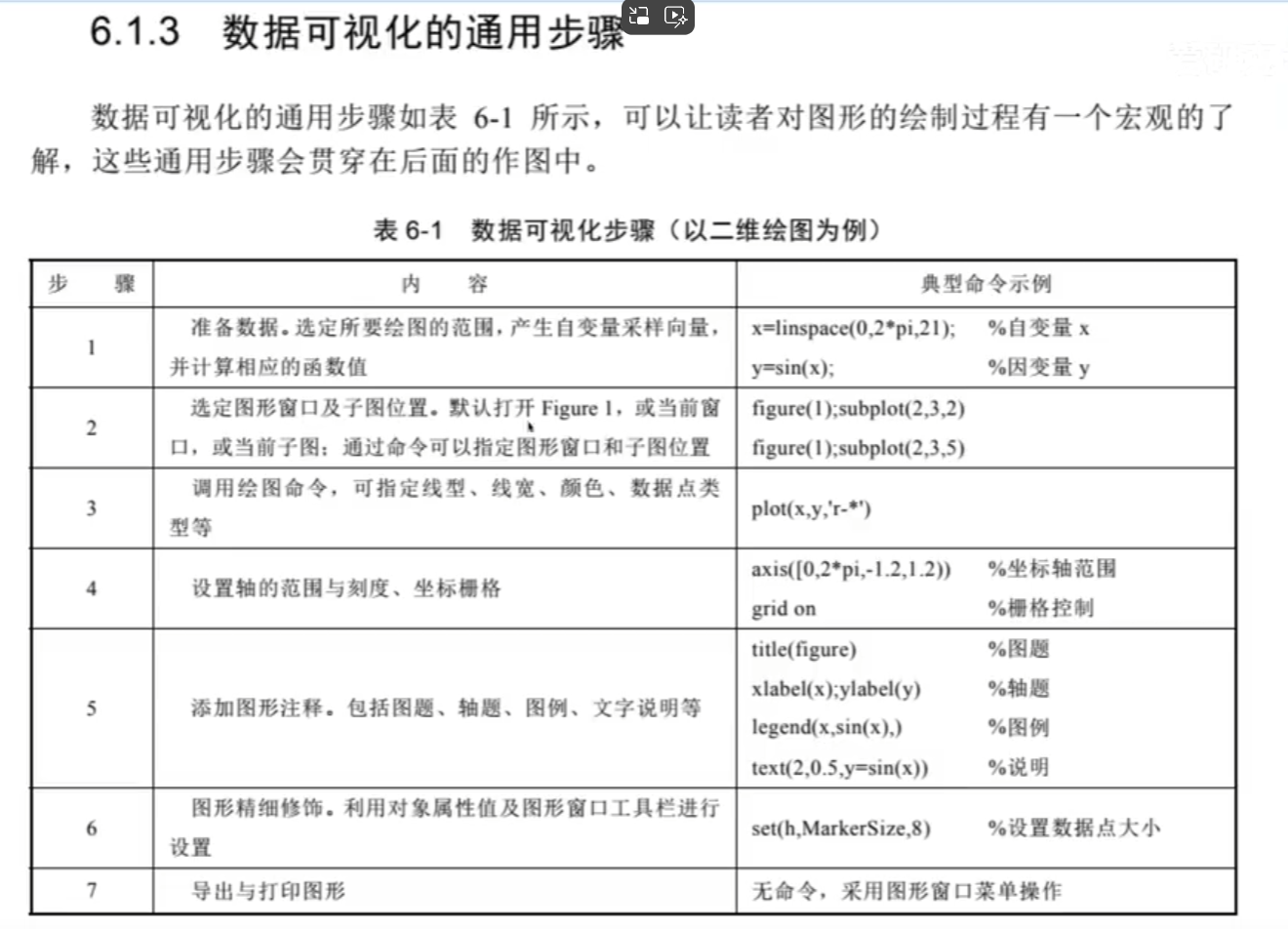
2.二维图形绘制

双坐标轴

hold on 叠图

hold off

子图

subplot(m,n,k)

3.三维图形

plot3

mesh 三维网格图

surf

3.二维特殊图形

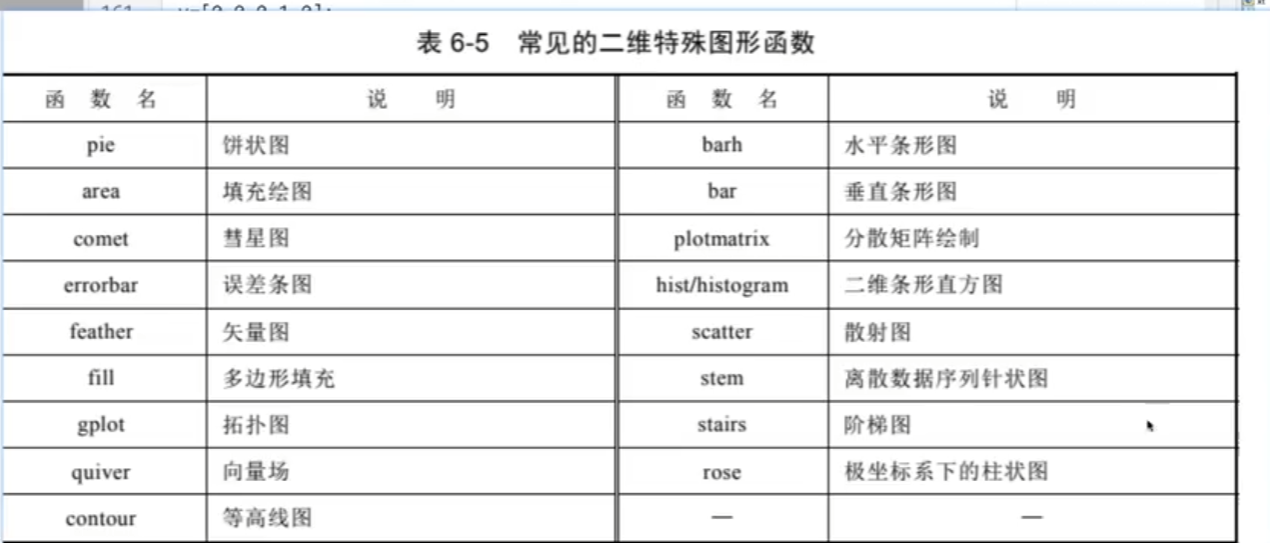
饼状图

阶梯图

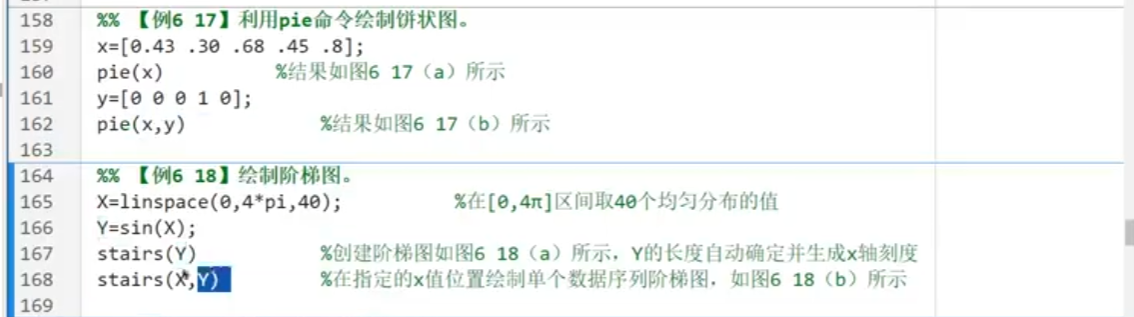
条形图

等高线

errorbar

4.三维特殊图形函数

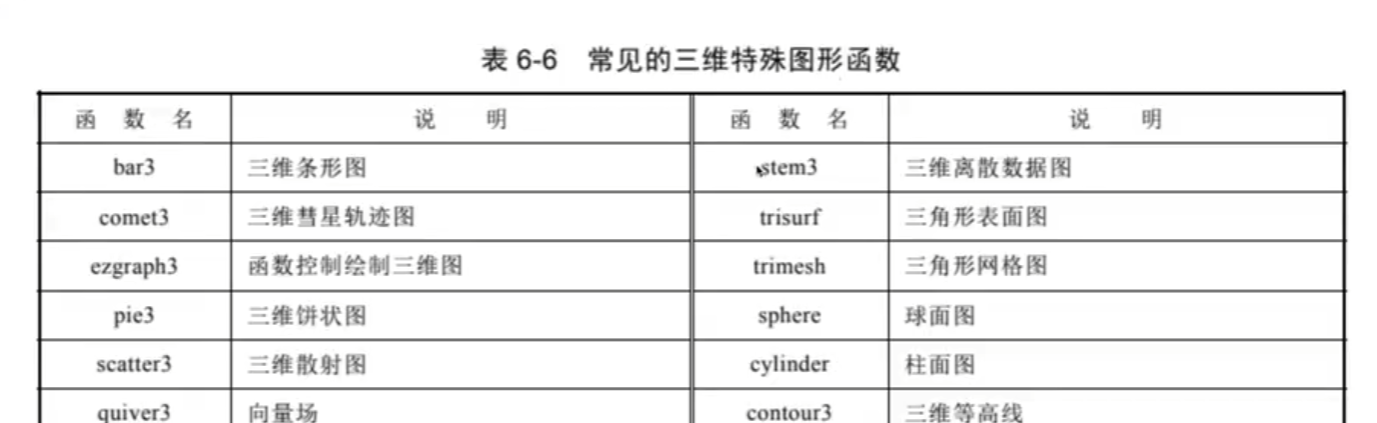
5.四维

七

1.坐标轴和图形标注

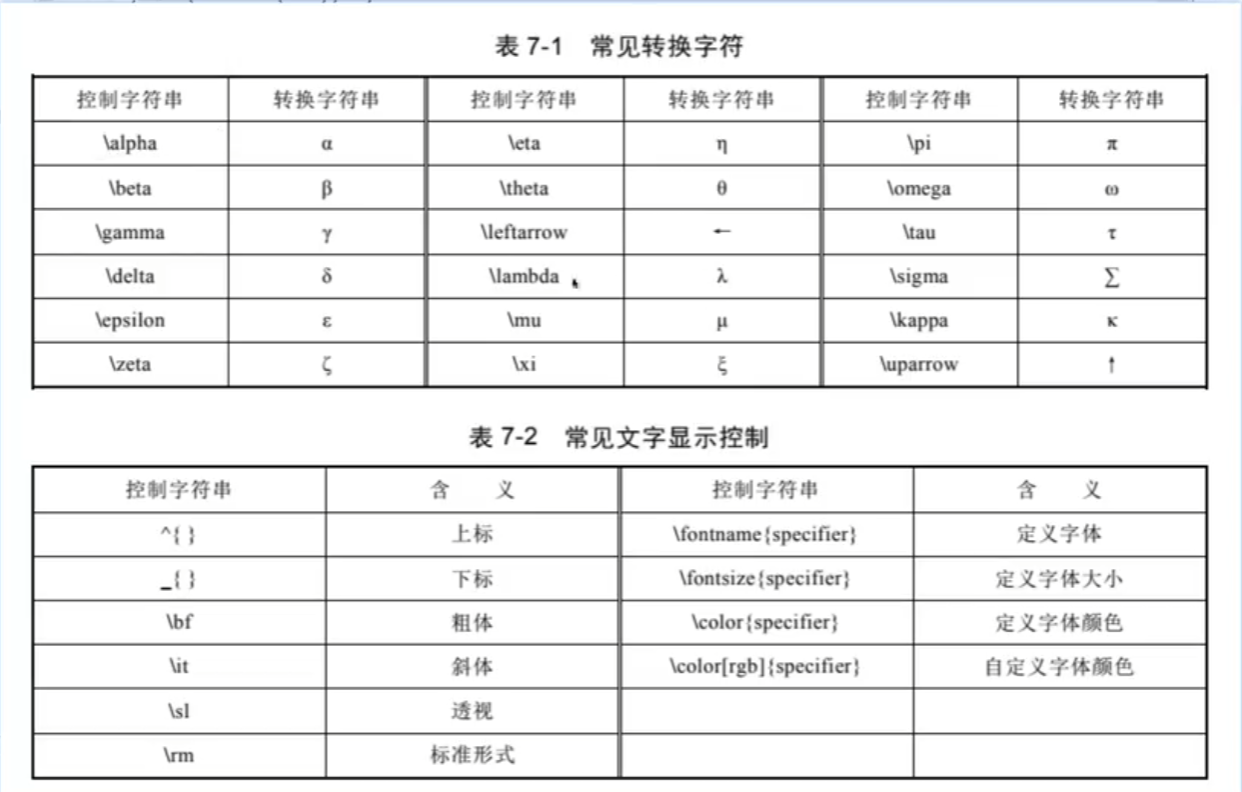
标注：

图例标注：legend

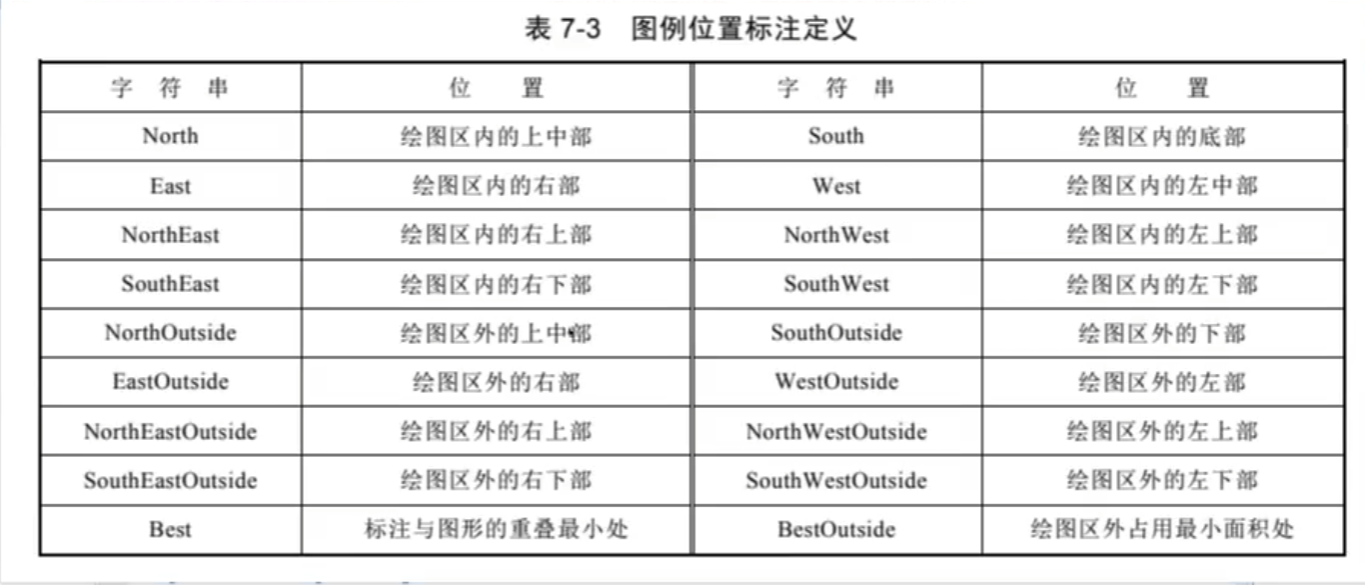
取点：ginput

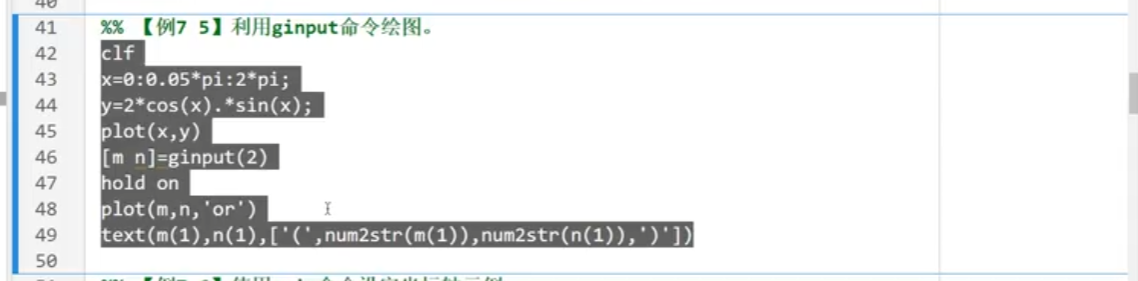
2.命令控制

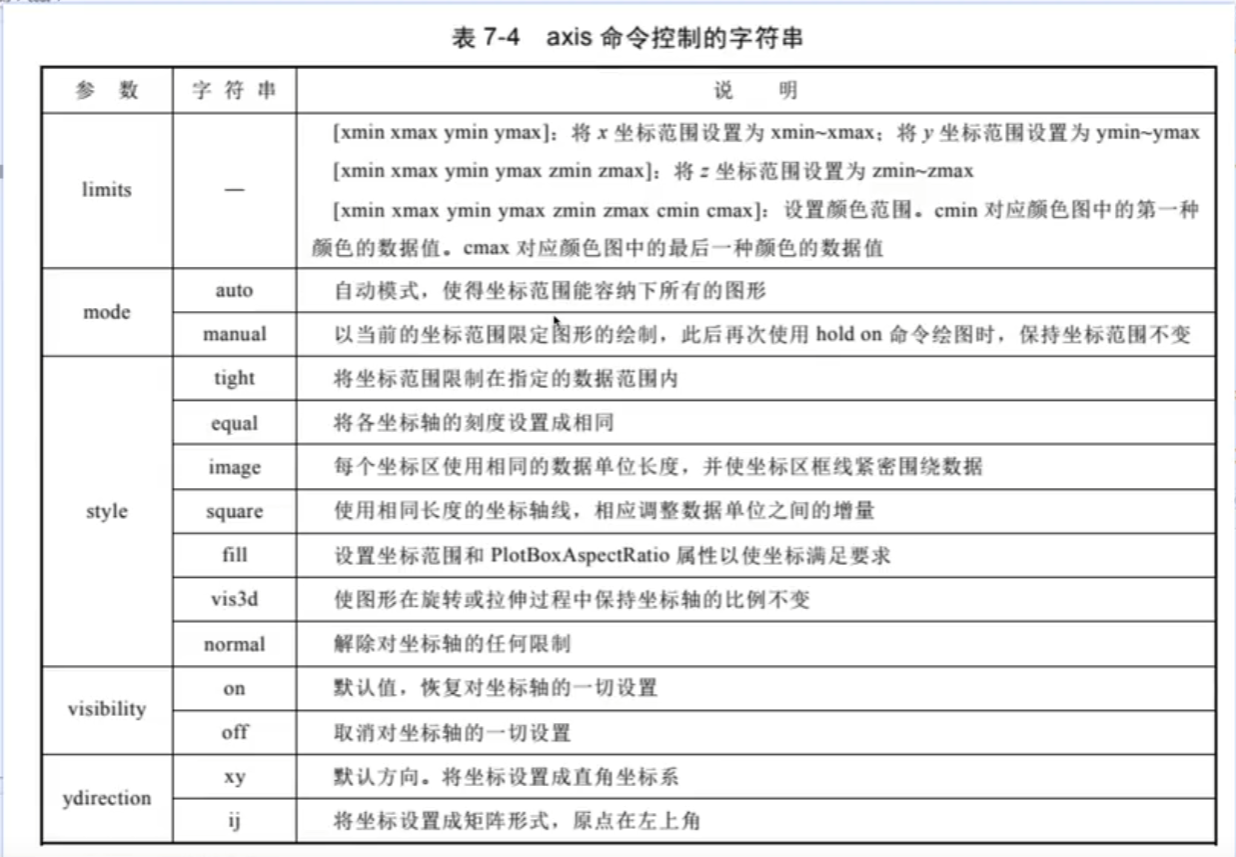
网格控制

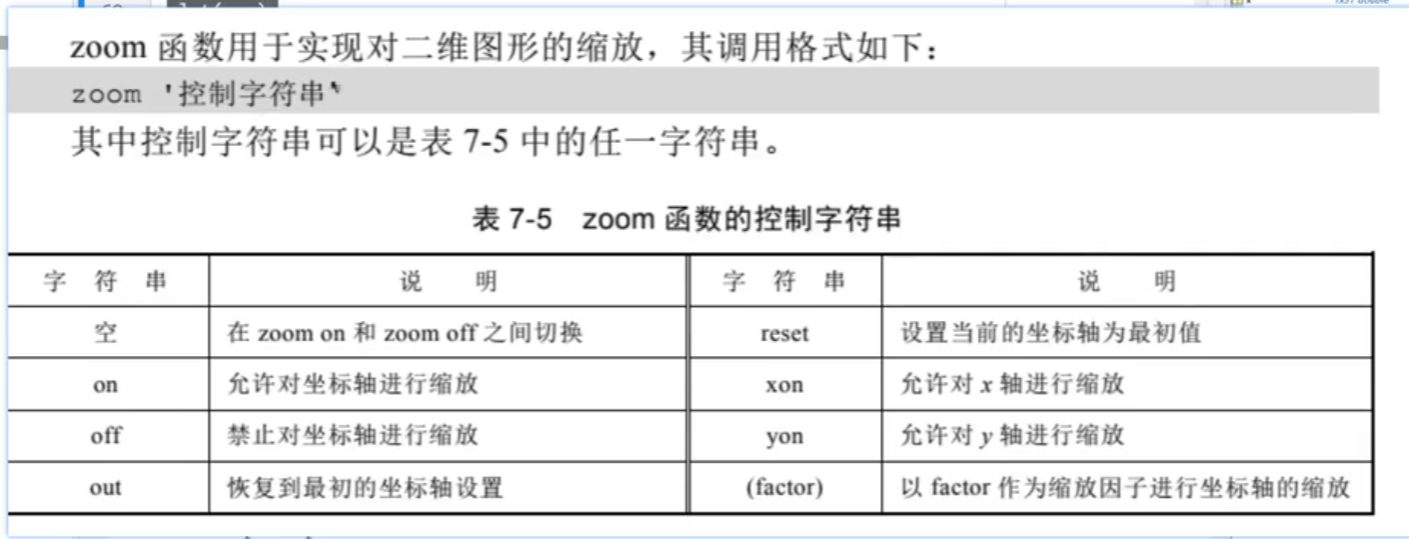
view:观察点

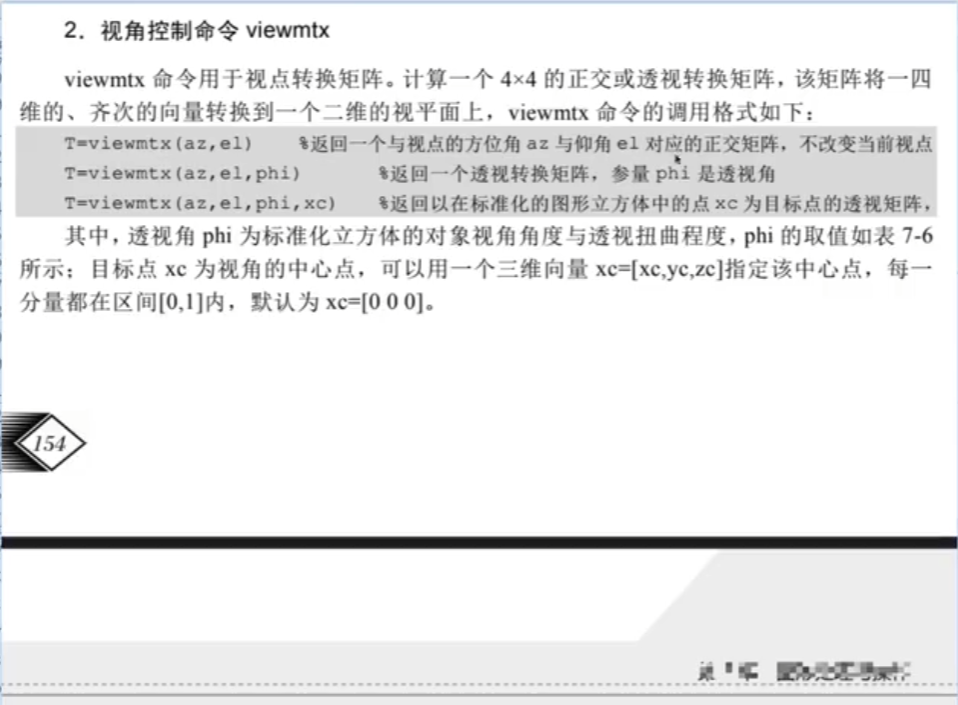
3.颜色

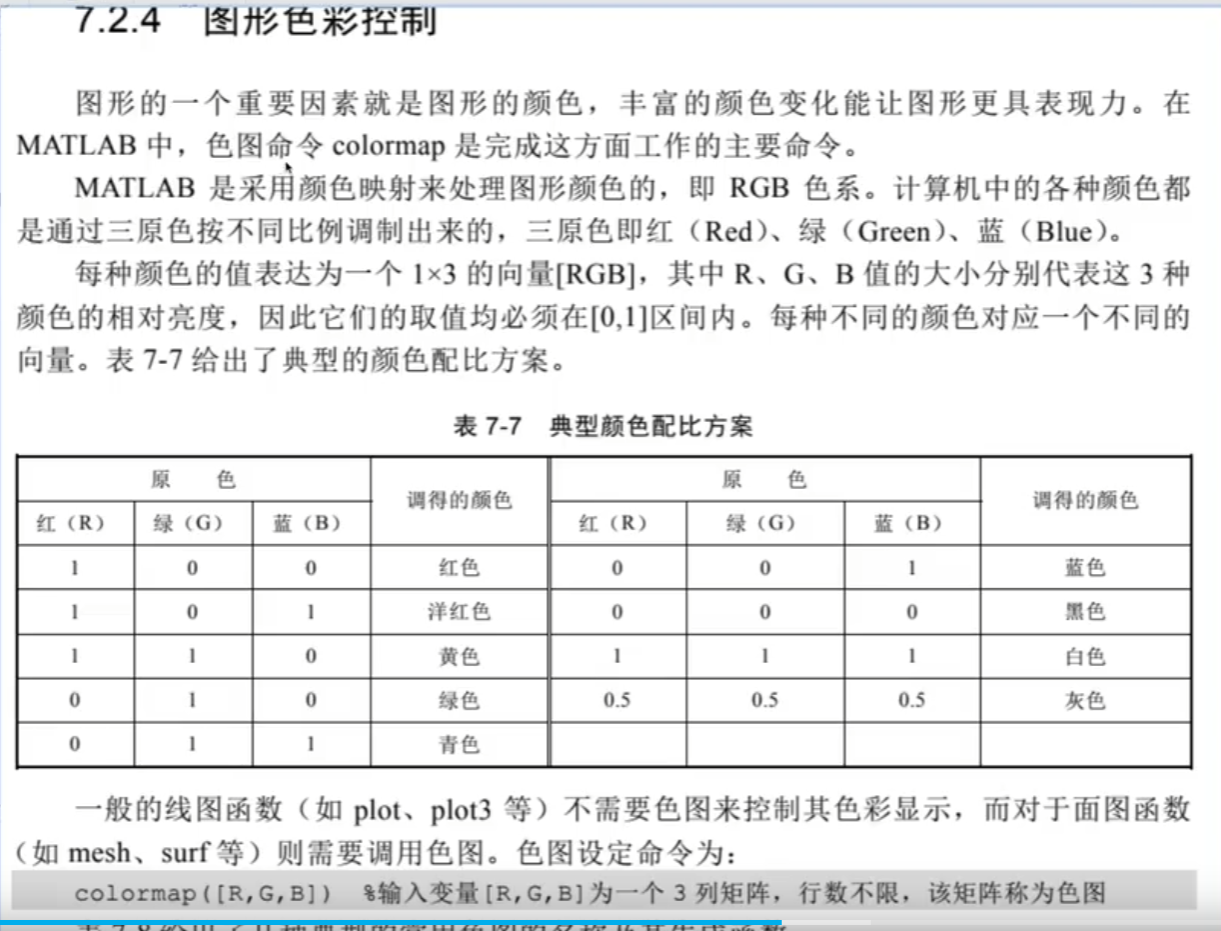
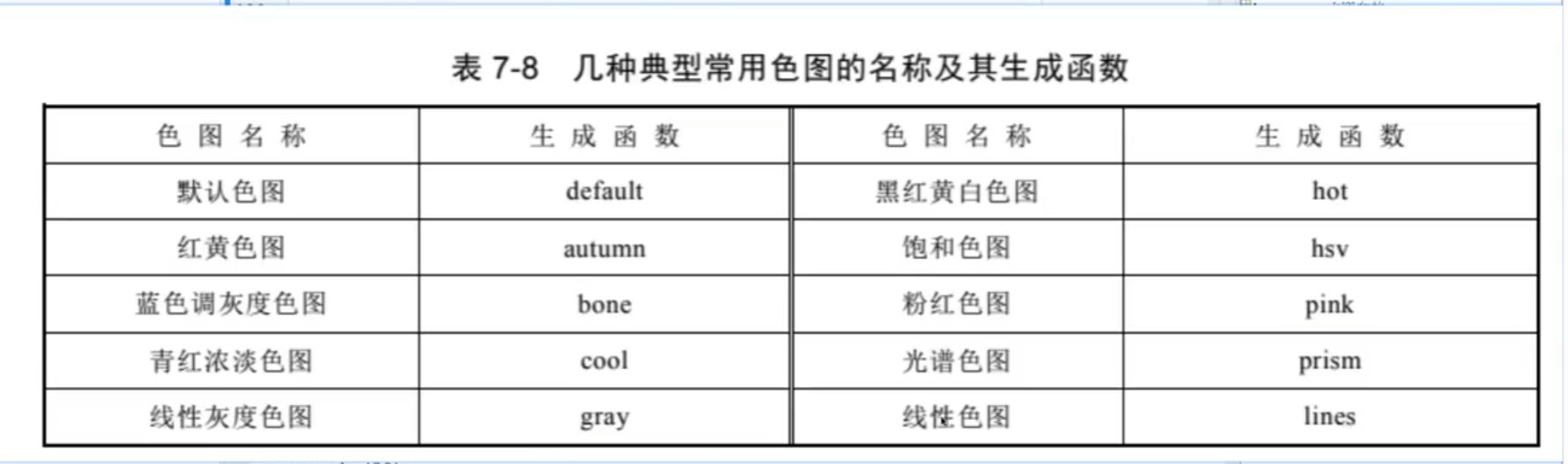
增亮：

颜色标尺：

背景色：

光照设置：

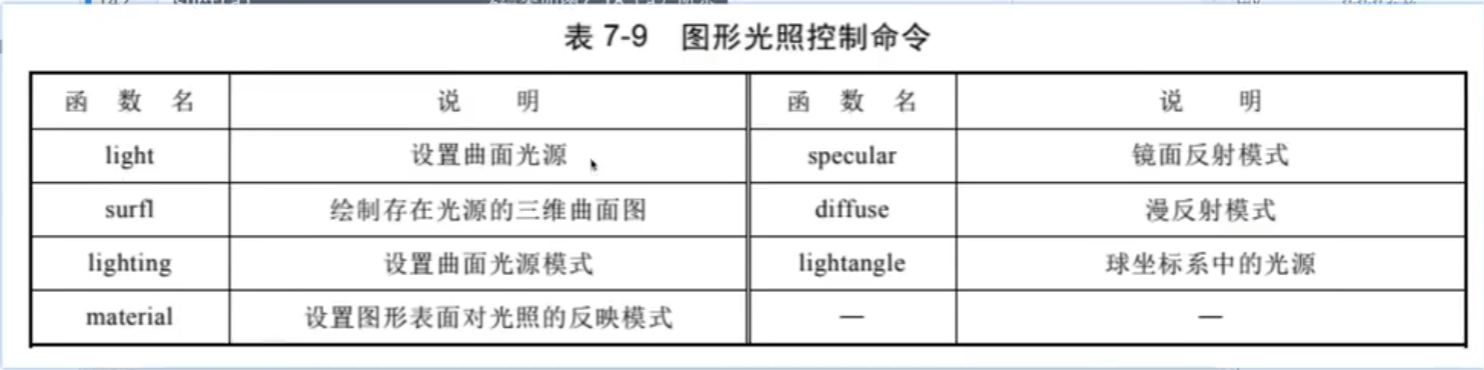
4.图形窗口

创建：

get获得图形窗口属性；

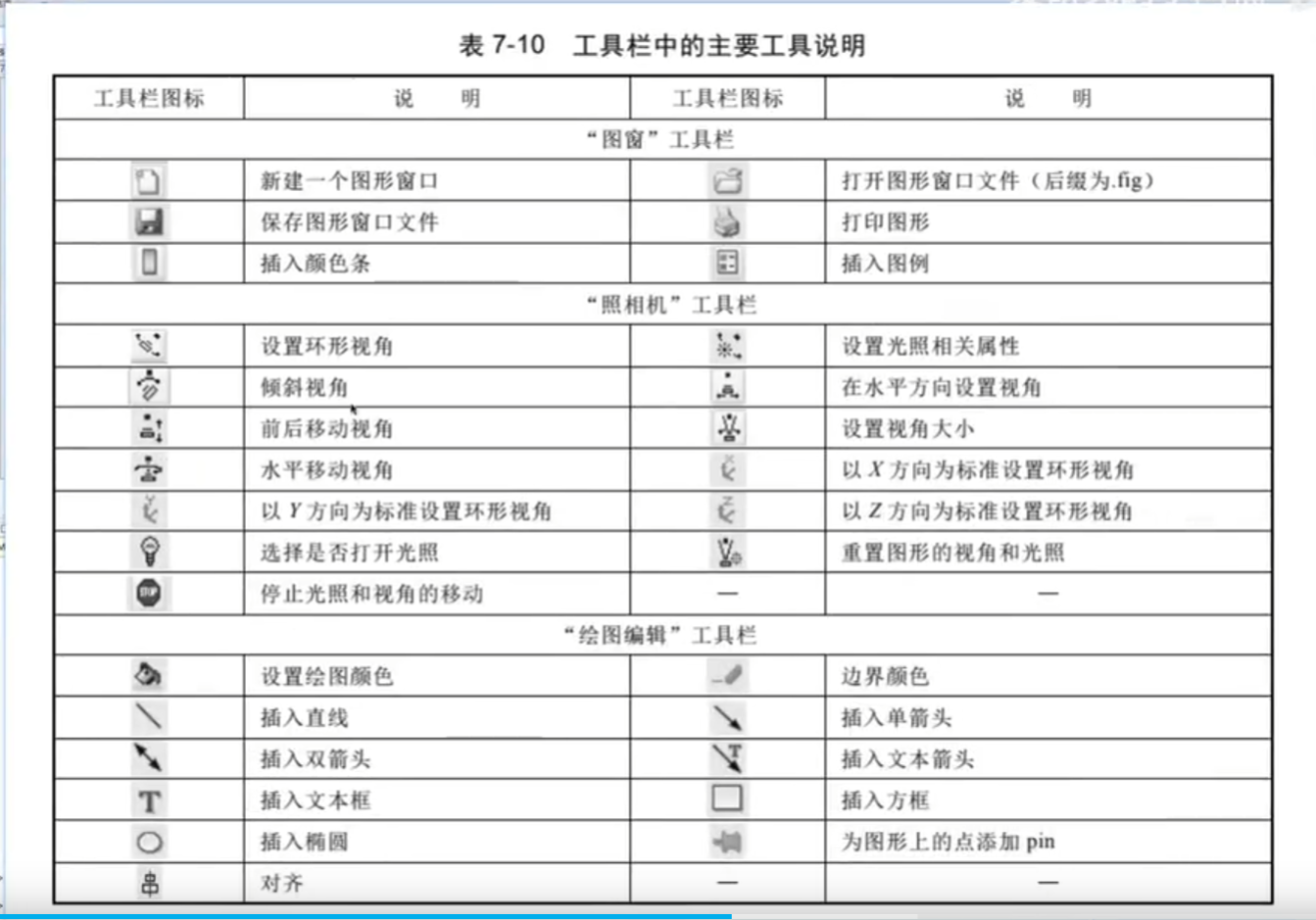
打印或输出：

八

1.数学函数->matlab语言

三角函数：

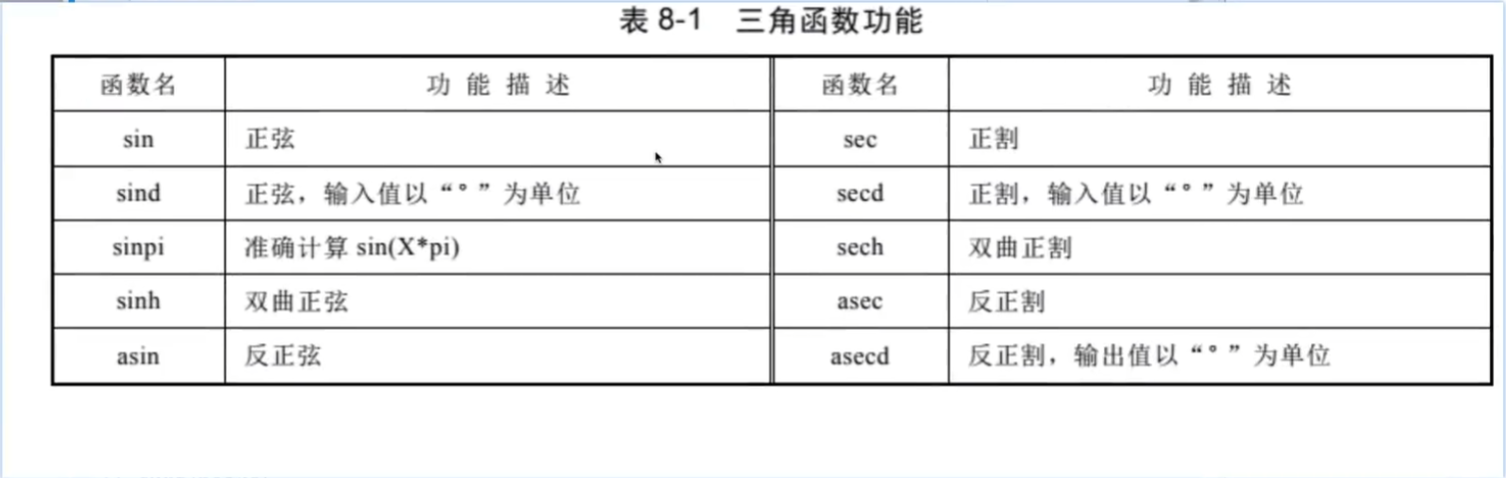
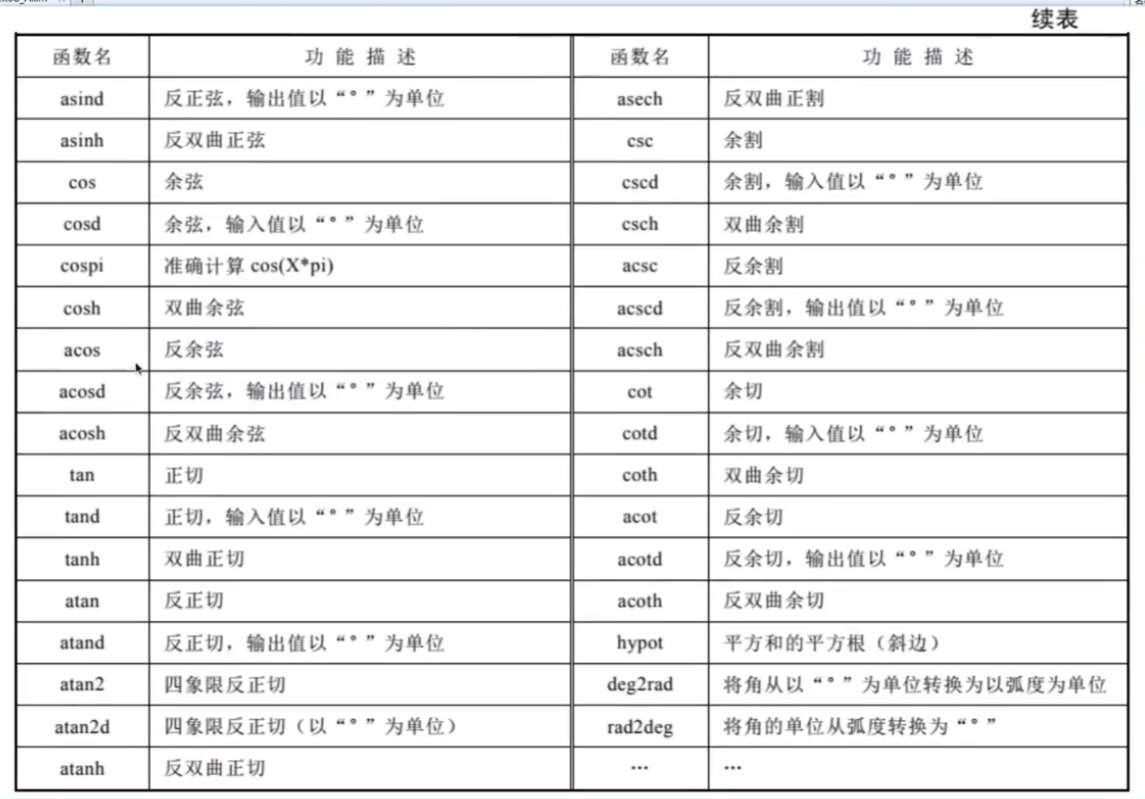
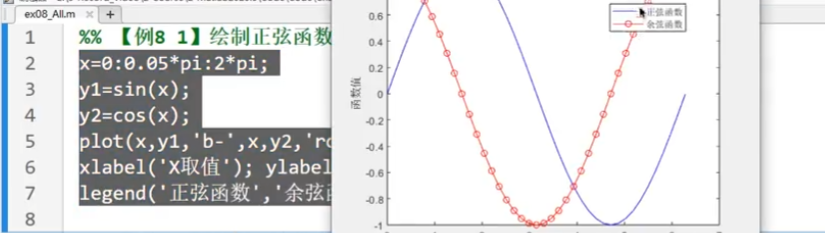
指数对数

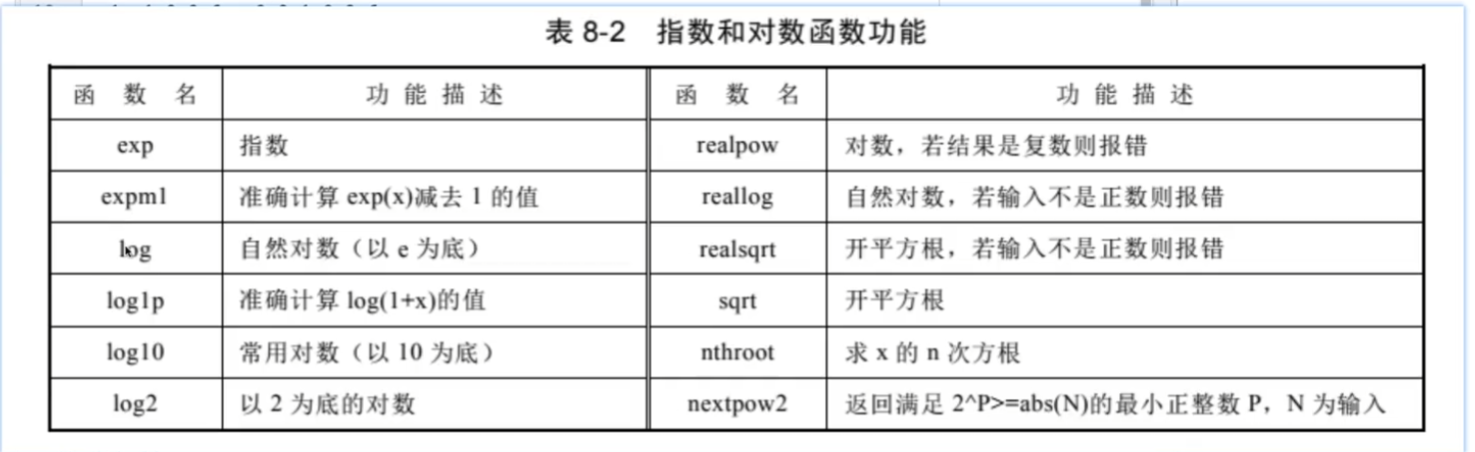复数

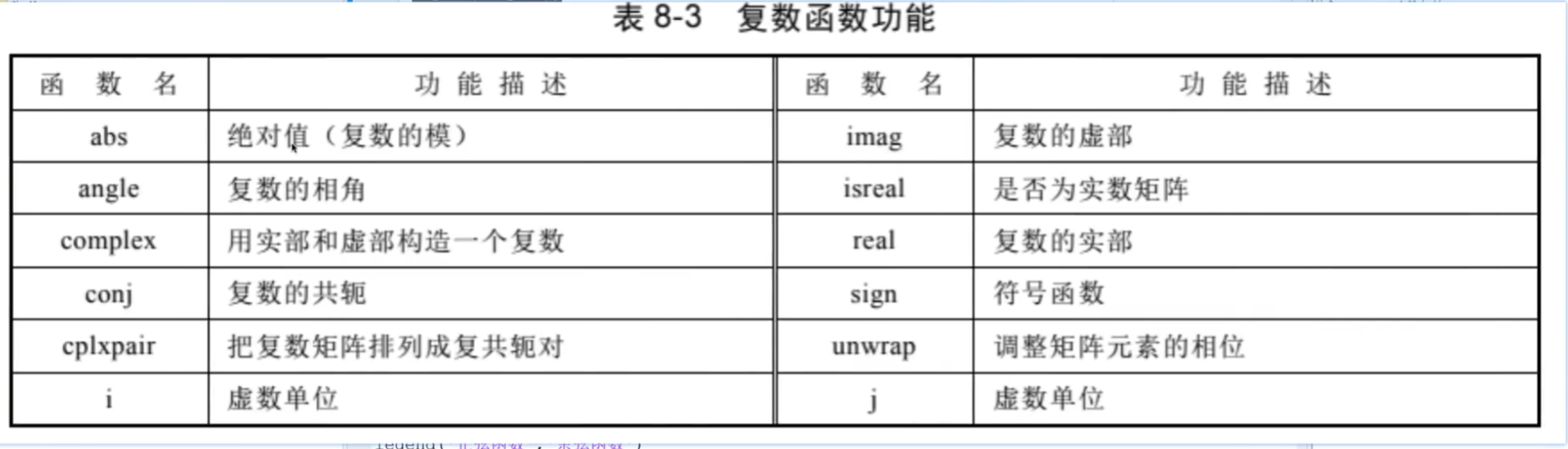
截断或求余

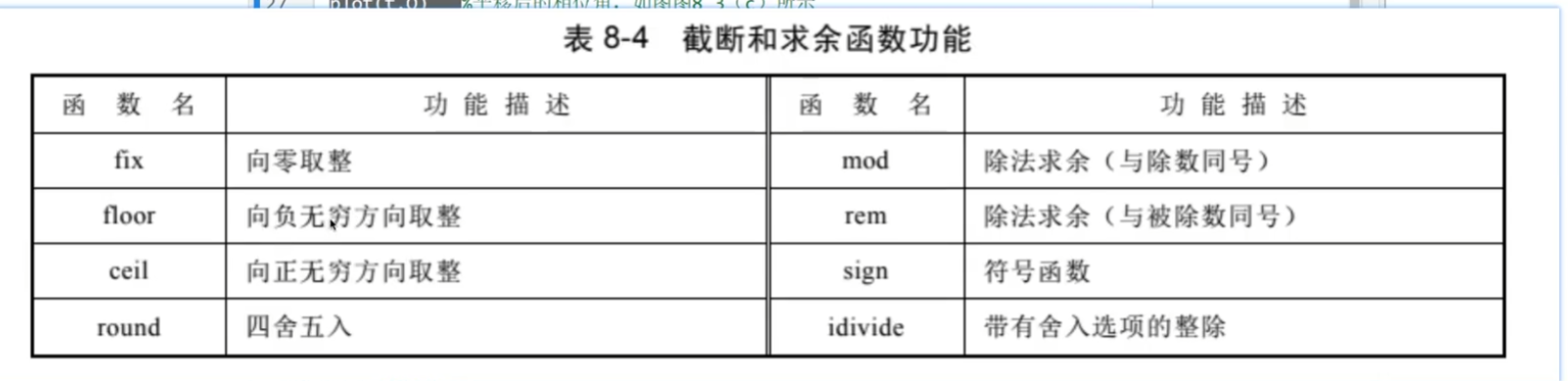
2.特殊函数

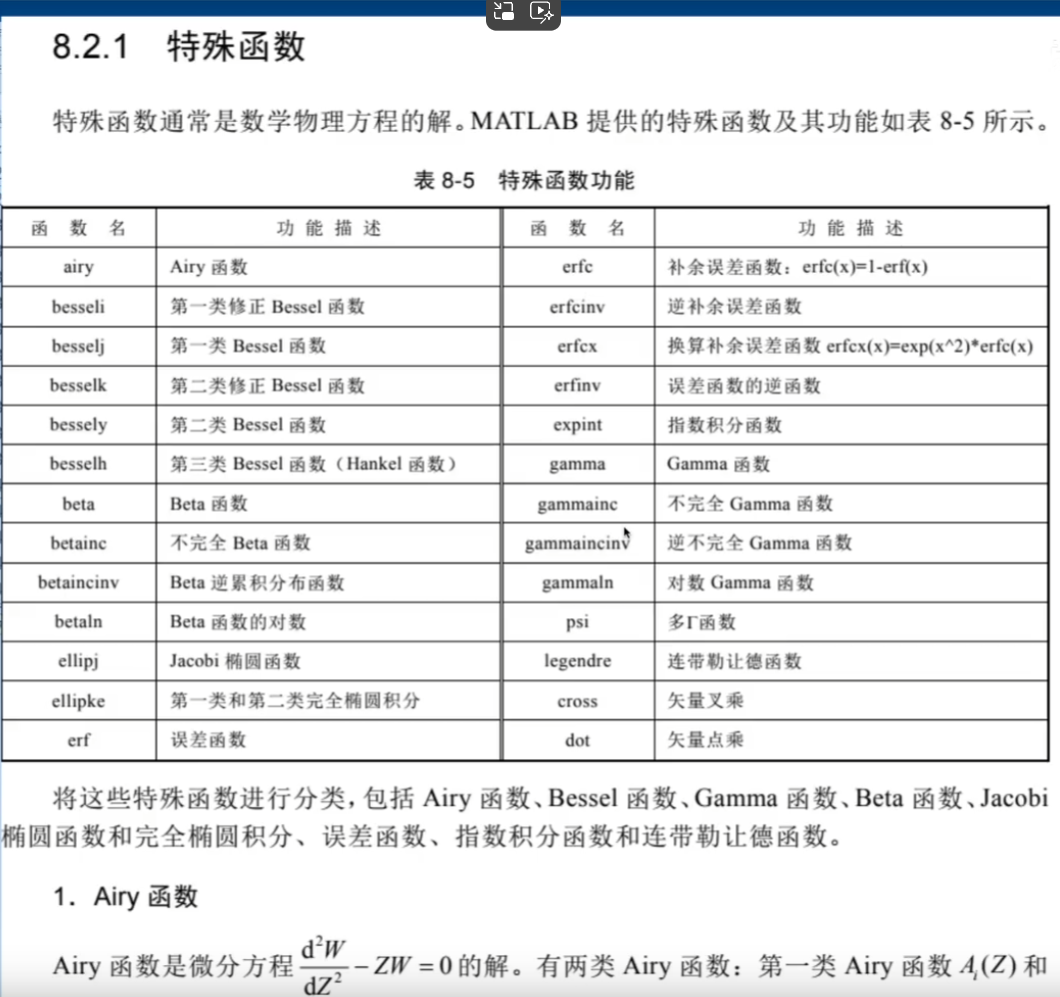
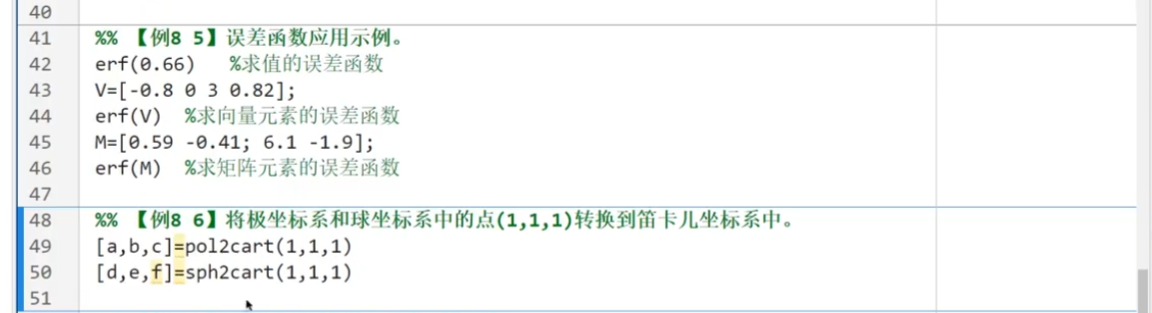
坐标变换函数：

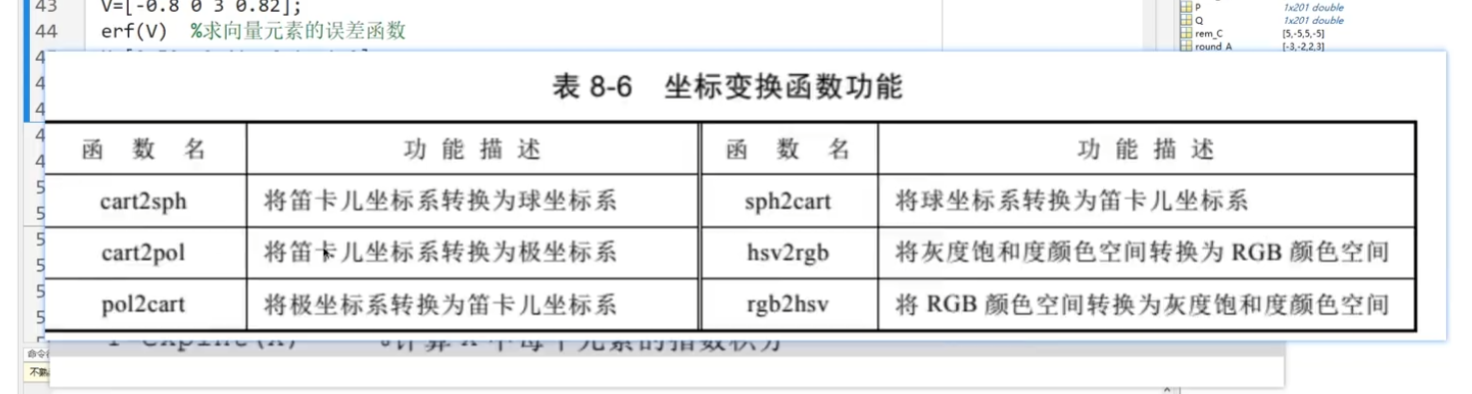数论函数：

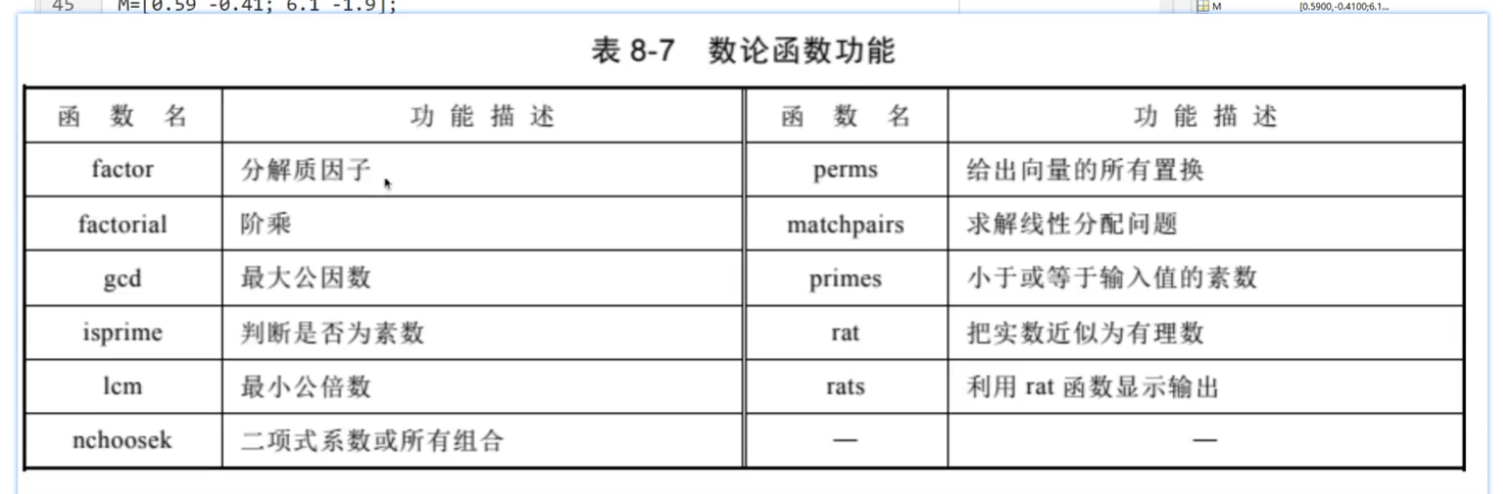
素数

九

1.符号运算

sym:

syms:

class

对象类型

符号运算

化简：

在 MATLAB 中，符号对象（symbolic object）和普通数值（numeric value）的区别主要体现在数据类型、计算方式、精度、用途等方面。下面我分学术和工程两个角度给你梳理一下。

1. 数据类型不同

特性	符号对象 (`sym`)	普通数值 (`double`, `single` 等)
数据类型	符号类型（Symbolic）	浮点数类型（Numeric）
存储形式	存储的是数学表达式或符号常量，不是近似值	存储的是有限精度的二进制浮点数
创建方式	`syms x; f = sym('pi');`	`a = 3.1416;`

2. 计算方式不同

符号对象
- 按符号推导规则运算，不会做浮点近似化。
- 能进行代数化简、微分、积分、解方程等符号运算。
- 例如：
```
syms x
diff(sin(x)^2, x)   % 结果是 2*sin(x)*cos(x)
```
普通数值
- 按数值计算规则运算，采用 IEEE 754 双精度（或单精度）近似。
- 无法直接进行代数化简，结果通常是近似数。
- 例如：
```
x = pi/3;
diff(sin(x)^2, x)   % 会报错，因为 x 只是数值
```

3. 精度与近似

符号对象 → 理论上无限精度（直到内存限制），保留 exact form，如 pi、sqrt(2)。
普通数值 → 有限精度（double 默认约 15~16 位有效数字），存在舍入误差。

举例：

sym(pi) - 4*atan(sym(1))   % 结果是 0（完全相等）
pi - 4*atan(1)             % 结果是 0（数值上接近，但可能不是精确 0）

4. 用途上的区别

符号对象
- 符号微积分（diff、int）
- 符号代数（simplify、factor）
- 精确解析解（solve）
- 高精度常数计算（配合 vpa 可指定位数）
普通数值
- 数值仿真（ODE 数值解、FFT 等）
- 工程数值计算（矩阵运算、统计分析等）
- 实时计算与信号处理

5. 转换关系

数值 → 符号
```
a = 3.14;
sym_a = sym(a);
```

符号 → 数值

x = sym('pi');
double(x)  % 转为 double 类型近似值

总结表

特性	符号对象 (sym)	普通数值 (double/single)
精度	理论无限精度	有限（~15 位）
运算方式	代数运算	浮点近似运算
用途	推导、符号解、精确计算	数值计算、仿真
内存占用	较大	较小
速度	慢	快

MATLAB 之所以要引入 符号对象（Symbolic Object），本质上是因为数值计算和数学推导的需求是两类完全不同的任务，而普通浮点数无法满足后一类任务的精确性与表达能力。

我分几个层次解释一下**“为什么需要符号对象”**。

1. 解决浮点数无法表达精确数学对象的问题

普通数值（double、single）存储的是近似值，而许多数学对象是无法用有限二进制小数精确表示的，比如：

π\pi、ee、2\sqrt{2}
分数 13\frac{1}{3}
无理数、代数式

浮点数在这些情况下会引入舍入误差，而符号对象则保留精确的数学形式：

sym(pi)   % 保留为 π，不是 3.1416...

2. 支持解析计算（Analytical Computation）

有些任务必须基于公式推导而不是近似数值：

符号微分（得出通用公式，而非某一点的导数）
符号积分（求出积分解析式）
符号解方程（求变量的精确表达式）
代数化简（消去公共因子、展开或因式分解）

例子：

syms x
diff(sin(x)^2, x)   % 结果是 2*sin(x)*cos(x)，而不是数值

这种能力在通信理论推导、信号公式变换等科研任务中很重要。

3. 实现高精度或任意精度计算

浮点数精度有限（double 约 15~16 位有效数字）。
当需要极高精度（如大数计算、误差敏感问题）时，浮点运算会累积误差。
符号对象配合 vpa（Variable Precision Arithmetic）可以按需求设置精度：

vpa(pi, 50)   % 计算 π 的 50 位有效数字

4. 支持数值与推导的混合工作流

在科研和工程计算中，经常需要先推导公式，再数值仿真。

推导阶段：用符号对象得到通用解析公式
仿真阶段：将符号公式转成数值函数，高速计算

这种模式可以减少人工推导错误，并在参数变化时自动更新公式。
例如 MU-MIMO 信道容量公式推导，可以用符号对象自动完成矩阵求导、迹运算等，再转为数值形式计算吞吐量。

5. 工程意义

避免手工推导的繁琐与易错性（符号引擎自动化）
保证结果的数学严谨性（不会因为舍入误差而得到错误结论）
提供可复用的解析模型（直接嵌入到数值计算中）

总结一句

符号对象的存在，是为了让 MATLAB 不仅能“算数”，还能“做数学”。
它让 MATLAB 既能做高速的数值计算（仿真），也能做精确的符号推导（理论分析），两者结合才适用于科研和高精度工程应用。

对，你的理解方向是对的，但我帮你精确化一下：符号变量并不是简单的“把数值换成变量”，而是把数值、变量甚至表达式都作为数学符号来处理，从而保留它们的精确结构。

1. 普通数值 vs 符号变量的本质区别

普通数值
- 只存储具体的数（例如 3.1416），MATLAB 只能对它做数值运算。
- 计算结果是数值，没有“通用性”。
符号变量 / 符号对象
- 存储的是一个数学符号（例如 xx、π\pi、2\sqrt{2}），可以在运算中保持符号形式，不直接化成数值。
- 能保留变量之间的关系，形成通用公式。
- 计算结果可以是另一个公式，而不是一个单一的数。

2. 例子直观比较

数值计算

x = pi/3;      % 数值
y = sin(x)^2;  % 已经是数值
diff(y, x)     % ❌ 报错，因为 y 是数值，不是表达式

符号计算

syms x
y = sin(x)^2;   % 符号表达式
dy = diff(y, x) % 结果: 2*sin(x)*cos(x)

这里 x 就是一个符号变量，不是具体数值，所以 MATLAB 可以对它做微分、积分、化简等操作。

3. 不只是变量，还能是“精确数”

符号对象还可以表示常数的精确形式：

sym(1/3)     % 保留为 1/3
1/3          % double 结果是 0.3333...

这意味着符号对象不仅仅是 “未知量 xx”，也可以是一个精确常数或一个代数式。

4. 总结你的那句话

符号变量并非简单地将数值替换为变量，而是以符号形式存储数学对象（变量、常数或表达式），使其在运算中保留解析结构，从而能够生成通用公式，而不仅是针对特定数值的结果。

MATLAB符号变量的创建和简单运算-CSDN博客

2.符号表达式

作为一个公式；

极限：

求和：

泰勒：

积分：

傅里叶变换：

eg:阶跃函数

拉普拉斯变换：

eg:

Z变换：

eg:

3.符号矩阵运算

4.符号方程求解

5.可视化数学分析窗口

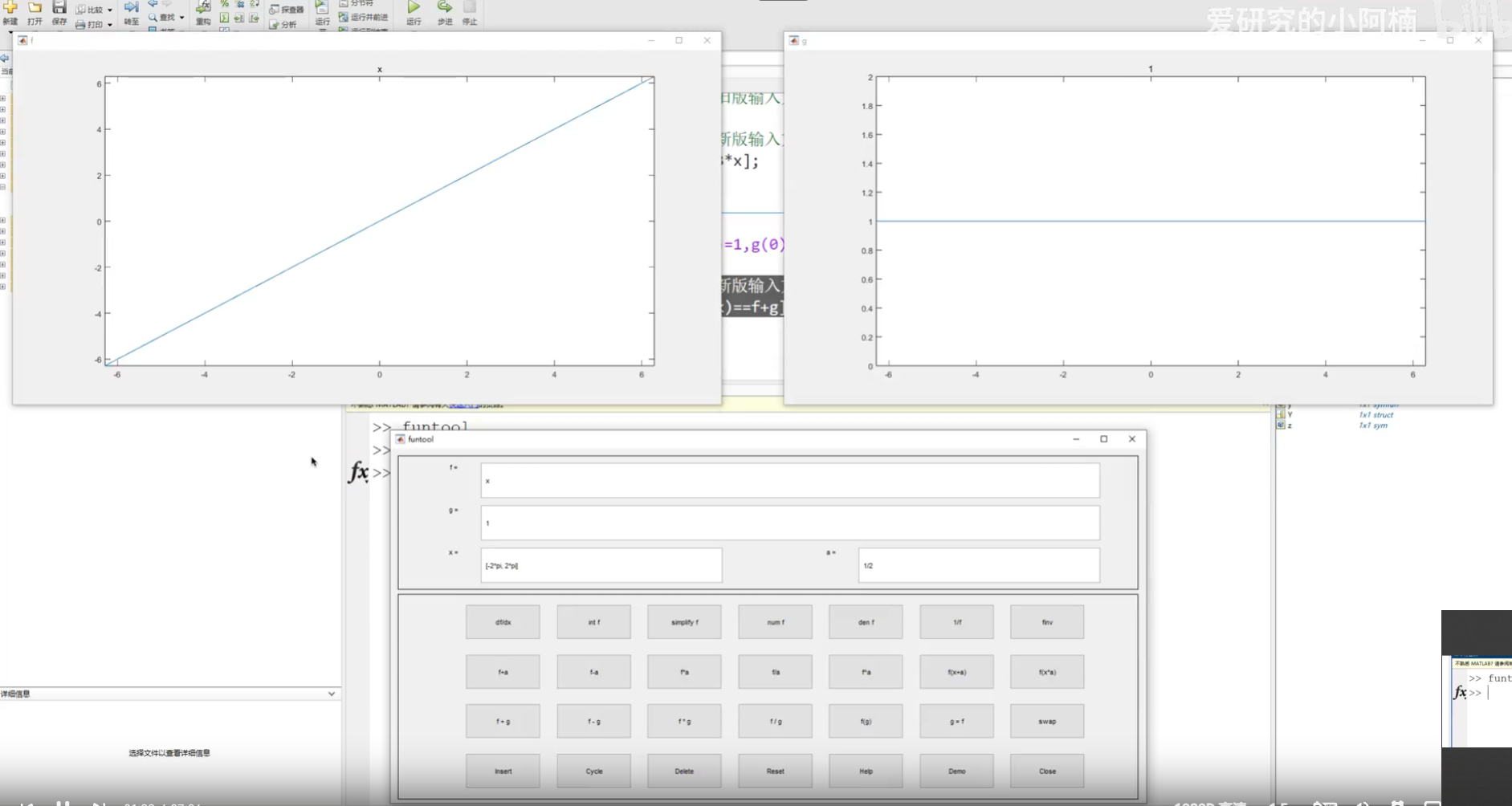泰勒级数分析：

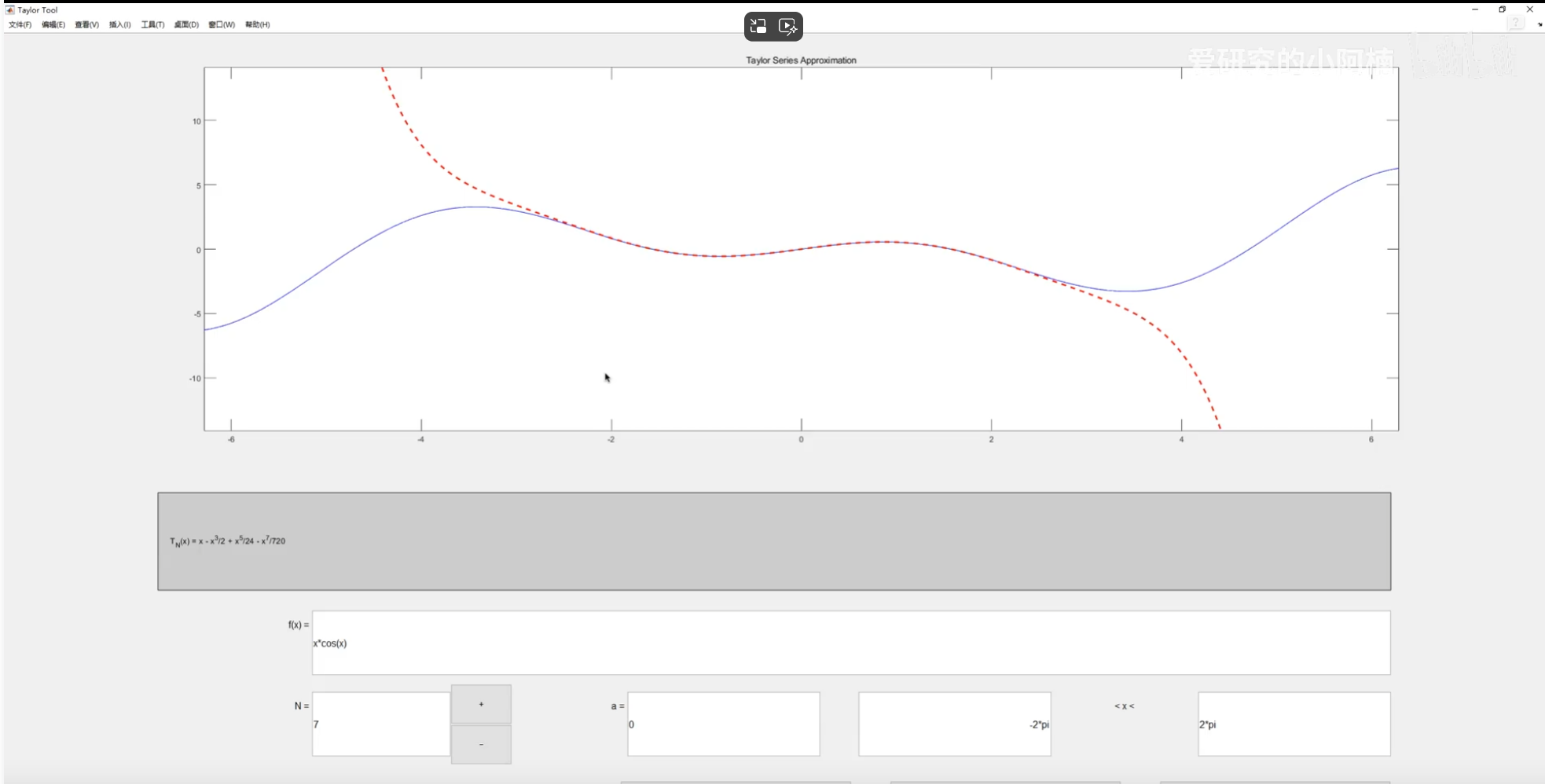
总结

是的，你现在已经抓到符号对象的核心特性了。
更精确地说，符号对象可以在两种“模式”下使用：

1. 作为“表达式”运算（符号模式）

所有变量、矩阵、公式保持符号形式，不转成具体数值。
运算结果依旧是另一个公式（而不是数）。
常见用途：推导公式、化简表达式、符号微分/积分、符号解方程等。

例子：

syms x y
f = sin(x)^2 + y^2;   % 符号表达式
dfdx = diff(f, x)     % 结果是 2*sin(x)*cos(x)

2. 对符号赋值求数值（数值模式）

可以用 subs 将符号变量替换成具体值，再用 double 转换为数值。
常见用途：公式推导完成后，用特定参数计算结果。

例子：

syms x y
f = sin(x)^2 + y^2;f_sub = subs(f, [x y], [pi/3 2]);  % 用具体值替换符号
num_result = double(f_sub)         % 转成 double 类型数值

3. 符号矩阵同理

推导阶段：符号矩阵保留精确结构，可做代数运算（行列式、逆、迹等）。
计算阶段：赋值并数值化求具体结果。

例子：

syms a b c d
A = [a b; c d];
det_A = det(A)          % 结果是 a*d - b*c （公式）
det_num = double(subs(det_A, [a b c d], [1 2 3 4])) % 结果是 -2

✅ 总结
你完全可以先用符号对象推导出通用表达式（保持解析精度），然后在需要时给符号变量赋值求数值。
这种“先符号推导 → 再数值计算”的模式特别适合通信系统公式推导 + 仿真这类科研任务，因为能避免手算公式的易错性，又能在仿真中复用公式。

十

数值计算：

求解方案：

高斯：

迭代法：对高阶

插值：

插值（Interpolation）在数学和信号处理里，指的是已知一组离散数据点，通过一定方法推算这些点之间未知位置的值。
它的本质就是——用一个连续函数去“穿过”这些已知点，然后用它估计中间点。

1. 插值的基本概念

假设你知道某函数在 x0,x1,…,xnx_0, x_1, \dots, x_n 处的值 y0,y1,…,yny_0, y_1, \dots, y_n，
插值的目标就是构造一个函数 P(x)P(x)，使得：

P(xi)=yi,i=0,1,…,nP(x_i) = y_i, \quad i=0,1,\dots,n

并用 P(x)P(x) 来估算这些已知点之间的任意位置的值。

2. 插值 vs 拟合

插值：要求插值函数严格通过所有已知数据点，没有偏差。
拟合：允许拟合曲线与数据点有一定误差，更关注整体趋势（比如最小二乘法拟合）。

3. 常见插值方法

方法	特点	举例
线性插值 (Linear)	相邻两点之间用直线连接，简单快速	`interp1(x, y, xq, 'linear')`
多项式插值 (Polynomial)	用高次多项式穿过所有点	拉格朗日插值、多项式插值公式
分段三次样条插值 (Cubic Spline)	分段三次多项式，保证一阶、二阶导数连续，曲线平滑	`interp1(x, y, xq, 'spline')`
二维/多维插值	适用于二维/三维数据	`interp2`、`interpn`
傅里叶插值	用周期信号的频域展开做插值	信号处理中的带限插值

4. MATLAB 中的插值示例

x = [0 1 2 3];
y = [0 1 0 1];xq = 0:0.1:3;  % 查询点
y_linear = interp1(x, y, xq, 'linear'); % 线性插值
y_spline = interp1(x, y, xq, 'spline'); % 样条插值plot(x, y, 'o', xq, y_linear, '-', xq, y_spline, '--');
legend('原始点', '线性插值', '样条插值');

5. 工程与科研中的意义

信号处理：将离散采样信号恢复到连续时间（带限插值）。
通信系统：定时同步、信道估计中利用插值获得未采样点的信道响应。
数值计算：在已知离散解的情况下估算中间值（如有限元分析）。
图像处理：图像缩放（最近邻插值、双线性插值、双三次插值）。

📌 一句话总结：

插值是“已知几个点，填补中间的空白”的过程，本质上是用一个连续函数通过这些点，然后用它预测未知点的值。

拟合：

polyfit 和 polyval 是 MATLAB 里一对常用的多项式拟合 + 计算工具，它们经常配合使用，但作用不同：

1. `polyfit` —— 求多项式系数（拟合阶段）

作用：给定一组数据点，找到一个指定阶数的多项式，使它在最小二乘意义下尽量接近这些数据。

语法：

p = polyfit(x, y, n)

x、y：数据点（长度相同的向量）
n：拟合多项式的阶数
p：返回一个行向量，包含从高次项到常数项的系数

例子：

x = [1 2 3 4];
y = [2.2 2.8 3.6 4.5];
p = polyfit(x, y, 1)   % 一阶拟合（直线）
% p 可能返回 [0.77 1.45]，对应 0.77*x + 1.45

2. `polyval` —— 计算多项式值（预测阶段）

作用：根据多项式系数，计算多项式在某些点的值。

语法：

y_fit = polyval(p, xq)

p：由 polyfit 返回的系数向量
xq：要计算的自变量值（可为标量、向量或矩阵）
y_fit：对应的多项式值

例子：

xq = 1:0.5:4;       % 查询点
yq = polyval(p, xq) % 根据拟合多项式预测

3. `polyfit` + `polyval` 组合使用示例

% 原始数据
x = [1 2 3 4];
y = [2.2 2.8 3.6 4.5];% 用二阶多项式拟合
p = polyfit(x, y, 2);% 生成更密的 x 值进行预测
xq = linspace(1, 4, 100);
yq = polyval(p, xq);% 绘图
plot(x, y, 'o', xq, yq, '-');
legend('原始数据', '二阶拟合曲线');

4. 和插值的区别

插值：要求曲线经过所有原始点（误差为 0）。
polyfit 拟合：允许曲线不经过所有点，目标是最小化总体误差（最小二乘法）。
多项式插值也能用 polyfit 实现，但拟合阶数要等于数据点数减 1（容易震荡）。

✅ 总结

polyfit：求多项式系数（拟合/插值）
polyval：用系数计算多项式值（预测/绘制）
常用组合：
先 polyfit 找系数 → 再 polyval 画曲线或求值

如果你需要，我可以帮你画一张**“polyfit vs 插值”对比图**，让你直观看到同一组点用线性拟合、二次拟合、样条插值的区别。这样你在科研（比如 MU-MIMO 信道曲线建模）时能快速判断用哪种方法。

问题

问题1：asv是什么类型文件

有时在存放m文件的文件夹中会出现*.asv
　　asv 就是auto save的意思，*.asv文件的内容和相应的*.m文件内容一样，用记事本和matlab都能打开它。它可以作为*.m文件的“备份”。
　　可以在preference中通过设置取消自动备份功能：file->preferences->editor/debugger-->auto save,uncheck "autosave on" checkbox ，把勾选去掉就行了。