7.17 Murnaghan–Nakayama 规则

我们已经成功地用基 $m_{\lambda }$、$h_{\lambda }$ 和 $e_{\lambda }$ 表示了 Schur 函数 $s_{\lambda }$。本节我们将考虑幂和对称函数 $p_{\lambda }$。一个斜分划 $\lambda /\mu$ 是连通的，如果其分拆图（视为实心方块的并集）的内部是一个连通（开）集。例如，分划 21/1 不是连通的。一个边缘条（或边界条或带图）是一个没有 $2\times 2$ 方块的连通斜分划。边缘条的一个例子是 86554/5443，其分拆图是

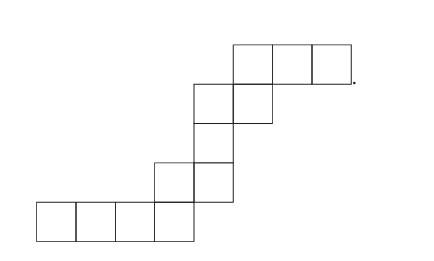
给定正整数 $a_1,\dots ,a_k$，存在唯一的边缘条 $\lambda /\mu$，其在第 $i$ 行有 $a_i$ 个方块（即 $a_i={\lambda }_i-{\mu }_i$）。由此可知，大小为 $n$ 的边缘条（在平移意义下）的数量是 $2^{n-1}$，即 $n$ 的分拆数。定义一个边缘条 $B$ 的高度 $\text{ht}(B)$ 为其行数减一。下面的结果展示了边缘条与对称函数之间的联系。

7.17.1 定理.

对于任意 $\mu \in \text{Par}$ 和 $r\in \mathbb{N}$，我们有
[s_{\mu} p_r = \sum_{\lambda} (-1)^{\text{ht}(\lambda / \mu)} s_{\lambda},]
(7.73)

求和遍历所有满足 $\lambda \supseteq \mu$ 且 $\lambda /\mu$ 是大小为 $r$ 的边缘条的分划 $\lambda$。

证明. 令 $\delta =(n-1,n-2,\dots ,0)$，并令所有函数均在变量 $x_1,\dots ,x_n$ 中。在方程 (7.53) 中令 $\alpha =\mu +\delta$ 并乘以 $p_r$。我们得到
[a_{\mu + \delta} p_r = \sum_{j=1}^{n} a_{\mu + \delta + r \epsilon_j},\tag{7.74}]

其中 ${ϵ}_j$ 是第 $j$ 位为 1 而其余为 0 的序列。将序列 $\mu +\delta +r{ϵ}_j$ 按降序排列。如果它有两个相等的项，那么它对 (7.74) 没有贡献。否则存在某个 $p\le q$ 使得
[\mu_{p-1} + n - p + 1 > \mu_q + n - q + r > \mu_p + n - p,]
在这种情况下 $a_{\mu +\delta +r{ϵ}_j}=(-1{)}^{q-p}{a}_{\lambda +\delta }$，其中 $\lambda$ 是分划
[\lambda = (\mu_1, \ldots, \mu_{p-1}, \mu_q + p - q + r, \mu_p + 1, \ldots, \mu_{q-1} + 1, \mu_{q+1}, \ldots, \mu_n).]
这样的分划恰好是那些使得 $\lambda /\mu$ 是大小为 $r$ 的边缘条 $B$ 的分划，并且 $q-p$ 恰好是 $\text{ht}(B)$。因此
[a_{\mu + \delta} p_r = \sum_{\lambda} (-1)^{\text{ht}(\lambda / \mu)} a_{\lambda + \delta}.]

除以 $a_{\delta }$ 并令 $n\to \infty$ 即得 (7.73)。

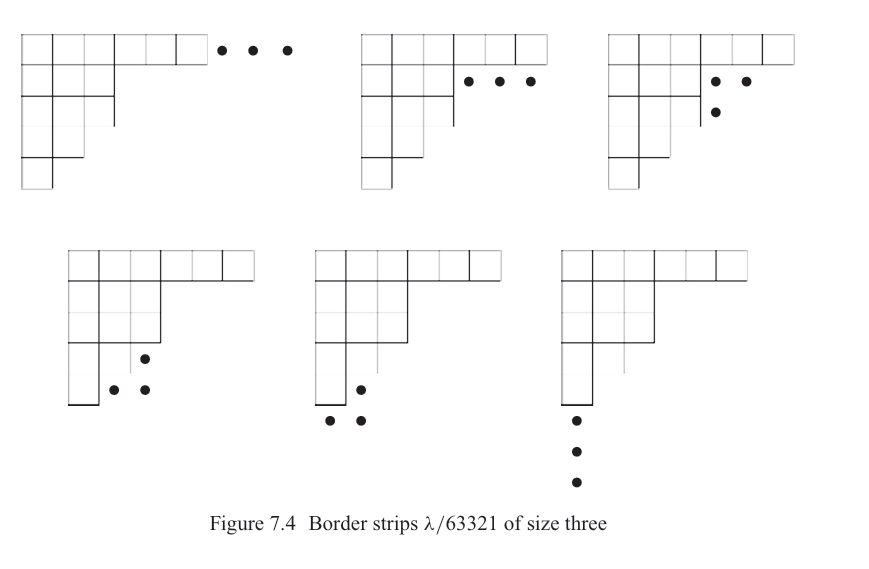
7.17.2 例. (a) 令 $\mu =63321$。可以添加到 $\mu$ 的大小为 3 的边缘条如图 7.4 所示。因此
[s_{63321} p_3 = s_{93321} + s_{66321} - s_{65421} - s_{63333} - s_{633222} + s_{63321111}.]

(b) 如上令 $\delta =(n-1,n-2,\dots ,0)$。只有两个大小为 2 的边缘条可以添加到 $\delta$，我们得到
[s_{\delta} p_2 = s_{n+1,n-2,n-3,\ldots,1} - s_{n-1,n-2,\ldots,2,1,1,1}.]

令 $\alpha =({\alpha }_1,{\alpha }_2,\dots )$ 是 $n$ 的一个弱分拆。定义一个形状为 $\lambda /\mu$（其中 $|\lambda /\mu |=n$）且类型为 $\alpha$ 的边缘条表（或边界条表）是将正整数分配给 $\lambda /\mu$ 的方块的一种赋值，满足：

(a) 每一行和每一列都是弱递增的，
(b) 整数 $i$ 出现 ${\alpha }_i$ 次，并且
© 被 $i$ 占据的方块集合形成一个边缘条或是空的。

等价地，可以将边缘条表视为一个分划序列 $\mu ={\lambda }^0\subseteq {\lambda }^1\subseteq \cdots \subseteq {\lambda }^k=\lambda$，使得每个斜分划 ${\lambda }^{i+1}/{\lambda }^i$ 是一个大小为 ${\alpha }_i$ 的边缘条（当 ${\alpha }_i=0$ 时包括空边缘条 $\varnothing$）。例如，数组

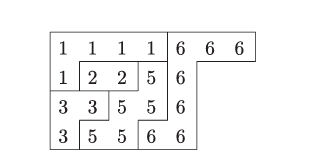
是一个形状为 7555 且类型为 $(5,2,3,0,5,7)$ 的边缘条表。（为了清晰起见，已画出边缘条的轮廓。）定义一个边缘条表 $T$ 的高度 $ht(T)$ 为
[\text{ht}(T) = \text{ht}(B_1) + \text{ht}(B_2) + \cdots + \text{ht}(B_k),]
其中 $B_1,\dots ,B_k$ 是 $T$ 中出现的（非空）边缘条。对于上面的例子，我们有 $\text{ht}(T)=1+0+1+2+3=7$.

如果我们将定理 7.17.1 迭代，依次用 $p_{{\alpha }_1},p_{{\alpha }_2},\dots$ 乘以 $s_{\mu }$，那么我们立即得到以下结果。

7.17.3 定理.

我们有
[ s_{\mu} p_{\alpha} = \sum_{\lambda} \chi^{\lambda/\mu}(\alpha) s_{\lambda}, \tag{7.75} ]
其中
[ \chi^{\lambda/\mu}(\alpha) = \sum_{T} (-1)^{\text{ht}(T)}, \tag{7.76} ]
求和遍历所有形状为 $\lambda /\mu$ 且类型为 $\alpha$ 的边缘条表 $T$.

在定理 7.17.3 中取 $\mu =\varnothing$ 可得：

7.17.4 推论

我们有
[ p_{\alpha} = \sum_{\lambda} \chi^{\lambda}(\alpha) s_{\lambda}, \tag{7.77} ]
其中 ${\chi }^{\lambda }(\alpha )$ 由 (7.76) 给出。

如果我们将自己限制在 $n\ge \ell (\lambda )$ 个变量中并应用定理 7.15.1，那么方程 (7.77) 可以重写为
[ p_{\alpha} a_{\delta} = \sum_{\lambda} \chi^{\lambda}(\alpha) a_{\lambda+\delta}. ]
因此我们得到 ${\chi }^{\lambda }(\alpha )$ 的以下“公式”：
[ \chi^{\lambda}(\alpha) = [x^{\lambda+\delta}] p_{\alpha} a_{\delta}. \tag{7.78} ]
使用方程 (7.75) 将 $s_{\lambda /\mu }$ 用幂和表示出来是容易的。这个结果（至少在 $\mu =\varnothing$ 的情况下）被称为 Murnaghan–Nakayama 规则。

7.17.5 推论

我们有
[ s_{\lambda/\mu} = \sum_{\nu} z_{\nu}^{-1} \chi^{\lambda/\mu}(\nu) p_{\nu}, \tag{7.79} ]
其中 ${\chi }^{\lambda /\mu }(\nu )$ 由 (7.76) 给出。

证明. 由 (7.75) 我们有
[ \chi^{\lambda/\mu}(\nu) = \langle s_{\mu} p_{\nu}, s_{\lambda} \rangle = \langle p_{\nu}, s_{\lambda/\mu} \rangle, ]
证明由命题 7.9.3 得出。

基 {sλ}\{s_\lambda\}{sλ​} 和 {pλ}\{p_\lambda\}{pλ​} 的正交性质转化为系数 ${\chi }^{\lambda }(\mu )$ 满足的正交关系。

7.17.6 命题

(a) 固定 $\mu$, $\nu$。则
[\sum_{\lambda} \chi^\lambda(\mu) \chi^\lambda(\nu) = z_\mu \delta_{\mu\nu}.]
(b) 固定 $\lambda$, $\mu$。则
[\sum_{\nu} z_\nu^{-1} \chi^\lambda(\nu) \chi^\mu(\nu) = \delta_{\lambda\mu}.]

证明. (a) 用 (7.77) 展开 $p_{\mu }$ 和 $p_{\nu }$ 并取 $⟨p_{\mu },p_{\nu }⟩$。
(b) 用 (7.79) 展开 $s_{\lambda }$ 和 $s_{\mu }$ 并取 $⟨s_{\lambda },s_{\mu }⟩$。

命题 7.17.6 等价于陈述矩阵 ${\left({\chi }^{\lambda }(\mu )z_{\mu }^{-1/2}\right)}_{\lambda ,\mu ⊢n}$ 是一个正交矩阵。这可以直接从这个事实看出：该矩阵是两个标准正交基 {sλ}\{s_\lambda\}{sλ​} 和 {pμzμ−1/2}\{p_\mu z_\mu^{-1/2}\}{pμ​zμ−1/2​} 之间的转移矩阵。

推论 7.17.4 的一个显著结果是系数 ${\chi }^{\lambda }(\alpha )$ 不依赖于 $\alpha$ 的项的顺序（因为对于乘积 $p_{\alpha }=p_{{\alpha }_1}{p}_{{\alpha }_2}\cdots$ 同样如此）。这个事实在获取关于数 ${\chi }^{\lambda }(\alpha )$ 的信息时可能具有重要价值。作为一个示例应用，我们提及以下结果。

7.17.7 命题

令 $\delta$ 为“阶梯形状” $\delta =(m-1,m-2,\dots ,1)$。则 $s_{\delta }$ 是奇次幂和 $p_1,p_3,\dots$ 的多项式。

证明. 我们需要证明如果 $\nu$ 有一个偶部分，则 ${\chi }^{\delta }(\nu )=0$。令 $\alpha$ 是 $\nu$ 的组成部分的一个排序，使得 $\alpha$ 的最后一个非零项 ${\alpha }_k$ 是偶数。因此，(7.76) 中的边缘条表 $T$ 具有这样的性质：标记为 $k$ 的方块形成一个大小为 ${\alpha }_k$ 的边缘条 $\delta /\nu$。但是每个边缘条 $\delta /\nu$ 都有奇数大小，所以这样的 $T$ 不存在。

关于命题 7.17.7 的逆命题，参见练习 54。

注记（供代数学者参考）. 对于 $\lambda ,\nu ⊢n$ 的系数 ${\chi }^{\lambda }(\nu )$ 有一个基本的代数解释：它们是对称群 ${\mathfrak{S}}_n$ 的不可约（常）表示的特征标值。更精确地说，${\mathfrak{S}}_n$ 的不可约特征标 ${\chi }^{\lambda }$ 以自然的方式由分划 $\lambda ⊢n$ 索引，并且 ${\chi }^{\lambda }(\nu )$ 是 ${\chi }^{\lambda }$ 在一个轮换类型为 $\nu$ 的元素 $w\in {\mathfrak{S}}_n$ 上的取值。因此，命题 7.17.6 正是不可约特征标满足的标准正交关系。现在从 (7.76) 可以立即看出（例如），特征标 ${\chi }^{\lambda }$ 的次数（或维数）由下式给出：
[\deg \chi^{\lambda} := \chi^{\lambda}(1n) = f^{\lambda}.]
因此，推论 7.12.6 与众所周知的结果一致：对于任何有限群 $G$，
[\sum_{\chi \in \widehat{G}} (\dim \chi)^2 = #G,]
其中 $\hat{G}$ 是 $G$ 的不可约特征标的集合。此外，推论 7.13.9 与不太为人所知的结果一致：
[\sum_{\chi \in \widehat{G}} \dim \chi = #{w \in G : w^2 = 1}]
当且仅当 $G$ 的每个（常）表示等价于一个实表示。关于对称函数与 ${\mathfrak{S}}_n$ 特征标之间联系的更多信息，请参见下一节以及本章的许多练习。