对于会有多次测量值的数据,用普通的回归去插补,往往会忽略掉数据个体本身的特点,毕竟多次的测量值其实就代表了数据个体的不稳定性,存在额外的干扰。
而RE的插补原理是结合个体本身的随机效应和群体的固体效应再加上截距进行插补的,比如学生A参加了月考,期中考,但是缺席了期末考,如果要插补期末考的成绩,除了班级的教学质量之外,学生个体的学习能力也很关键,可能存在学生本身是学霸,成很稳定,也可能存在学生是中游水平,期中考试超常发挥,需要综合考量。
以下是一个例子:
library(nlme)
library(ggplot2)
# 生成模拟数据:10个患者,每个患者测量3-5次
set.seed(123)n_patients <- 10
time_points <- 5# 创建数据框
data <- data.frame(patient_id = rep(1:n_patients, each = time_points),time = rep(1:time_points, times = n_patients),treatment = rep(rbinom(n_patients, 1, 0.5), each = time_points) # 治疗组(0/1)
)# 生成因变量y(含随机效应和噪声)
data$y <- 2 * data$treatment + rep(rnorm(n_patients, sd = 1.5), each = time_points) + rnorm(nrow(data), sd = 1)# 人为制造缺失值(MAR:缺失概率与时间相关)
data$y[data$time > 3 & runif(nrow(data)) > 0.7] <- NA
head(data, 15)# 拟合线性混合模型(LMM)
model <- lme(y ~ treatment + time, random = ~ 1 | patient_id, data = data, na.action = na.exclude)# 预测缺失值(插补)
data$y_imputed <- ifelse(is.na(data$y), predict(model, newdata = data), data$y)# 查看插补结果
head(data[is.na(data$y), c("patient_id", "time", "y", "y_imputed")], 10)ggplot(data, aes(x = time, y = y_imputed, group = patient_id, color = factor(treatment))) +geom_line(alpha = 0.6) +geom_point(aes(y = y), size = 2, na.rm = TRUE) + # 原始观测点(含缺失)labs(title = "RE插补效果(红色点为原始观测值)", x = "时间", y = "观测值", color = "治疗组") +theme_minimal()
输出:
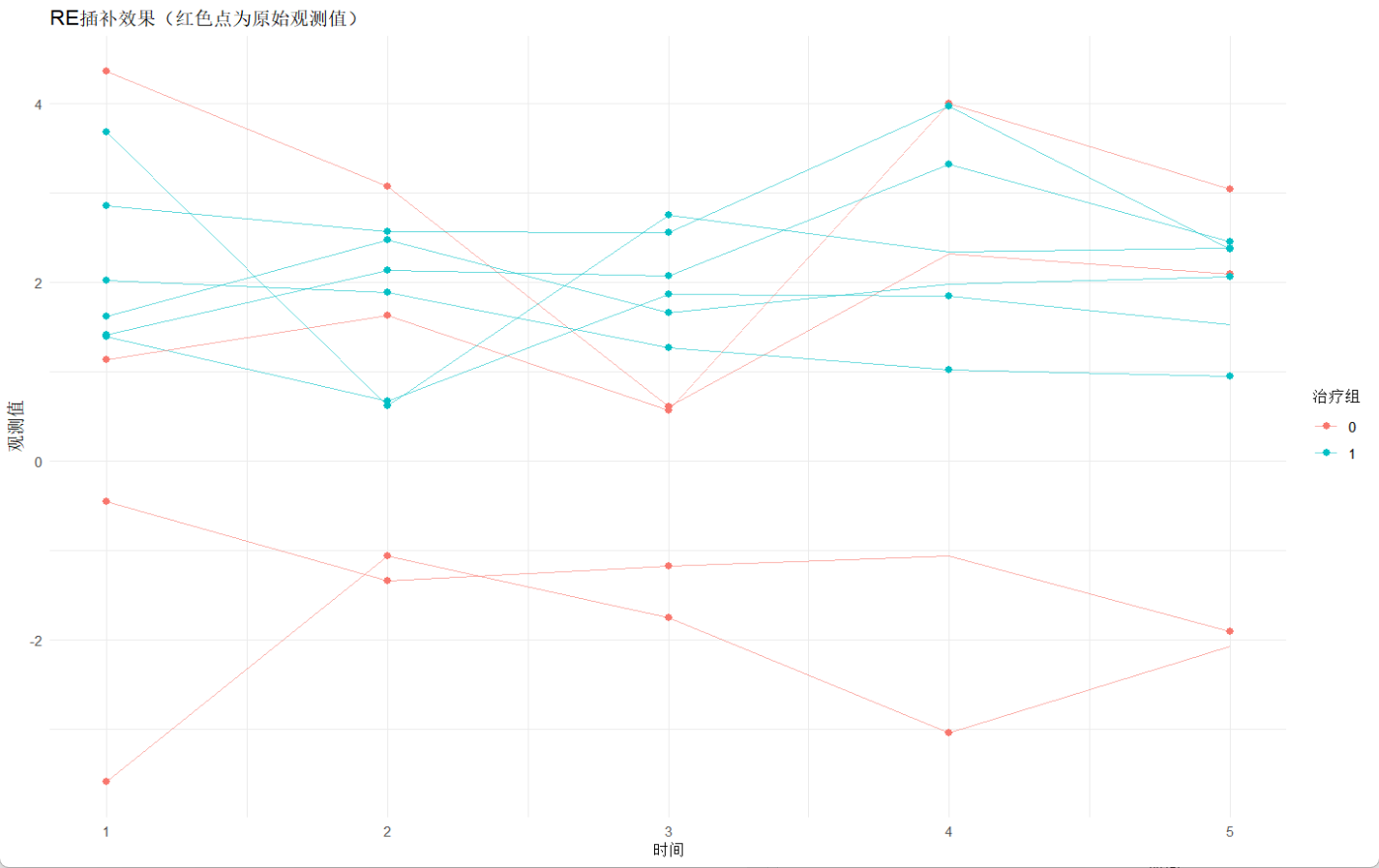
从图中可以看到,尽管RE能考虑随机效应加固体效应,但是如果样本本身存在离散值或者波动比较大的话,那么不管用什么方法去插补效果都比较差。



)







)



)
的编程实现方法:1、数据包格式定义结构体2、使用队列进行数据接收、校验解包)

)
