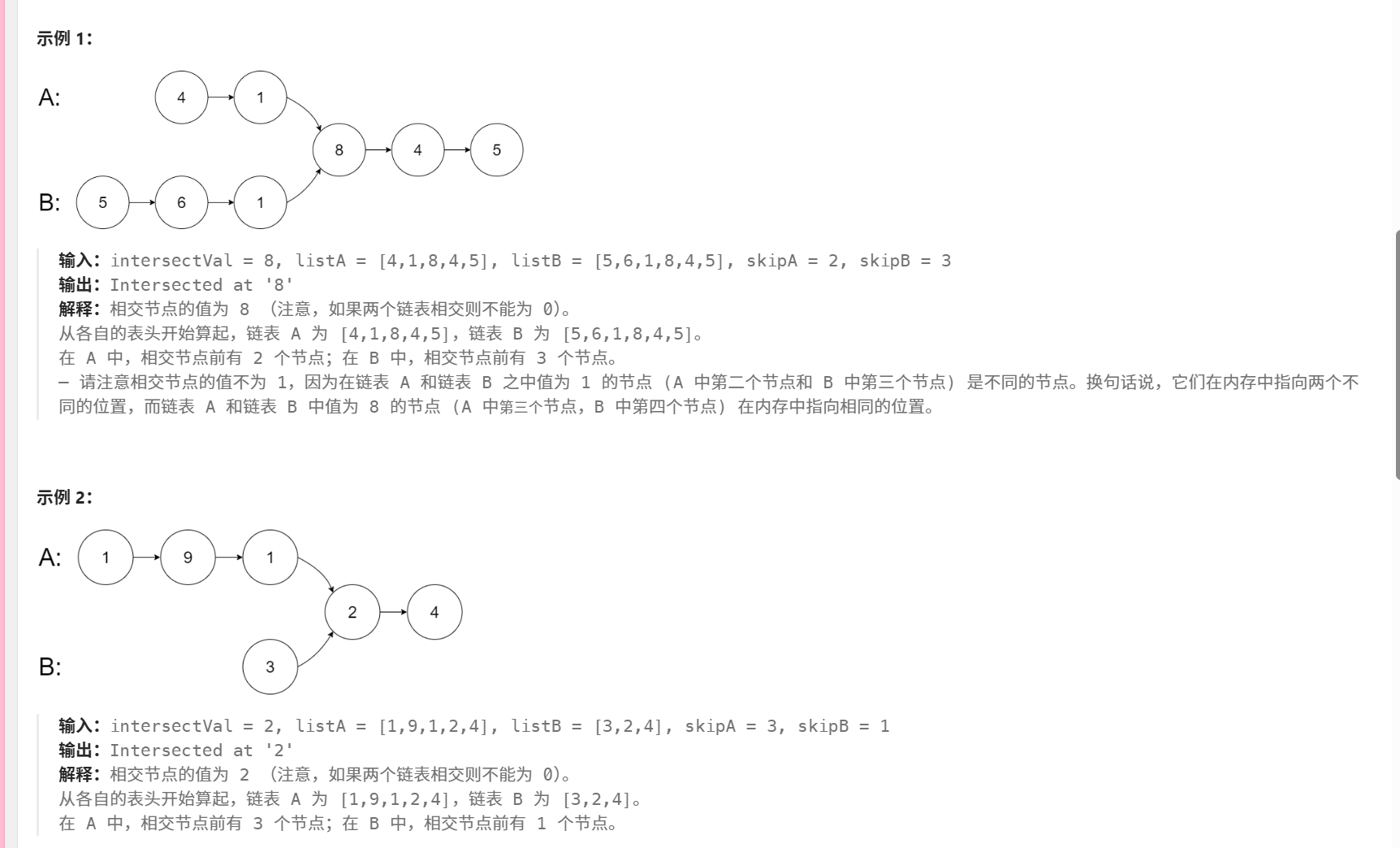
160. 相交链表


/*** Definition for singly-linked list.* public class ListNode {* int val;* ListNode next;* ListNode(int x) {* val = x;* next = null;* }* }*/
public class Solution {/*** 查找两个链表的相交节点* @param headA 第一个链表的头节点* @param headB 第二个链表的头节点* @return 相交的节点,如果不相交则返回null*/public ListNode getIntersectionNode(ListNode headA, ListNode headB) {// 使用HashSet来存储已经访问过的节点Set<ListNode> visited = new HashSet<ListNode>();// 遍历第一个链表headA,将所有节点存入HashSetListNode temp = headA;while (temp != null) {visited.add(temp); // 将当前节点加入已访问集合temp = temp.next; // 移动到下一个节点}// 遍历第二个链表headB,检查每个节点是否在HashSet中存在temp = headB;while (temp != null) {// 如果当前节点已存在于HashSet中,说明是相交节点if (visited.contains(temp)) {return temp; // 返回相交节点}temp = temp.next; // 移动到下一个节点}// 如果遍历完headB都没有找到相交节点,返回nullreturn null;}
}代码解读:寻找两个链表的交点
这段代码实现了在Java中寻找两个单链表相交节点的功能。以下是详细解读:
方法签名
public ListNode getIntersectionNode(ListNode headA, ListNode headB)
参数:两个链表的头节点
headA和headB返回值:两个链表相交的节点,如果不相交则返回
null实现思路
代码使用了哈希集合的方法来解决问题,具体步骤如下:
遍历第一个链表:将链表A的所有节点存入一个HashSet中
遍历第二个链表:检查链表B的每个节点是否存在于HashSet中
找到交点:如果存在,则该节点就是交点;如果遍历完都没有找到,则返回null
代码逐行解析
Set<ListNode> visited = new HashSet<ListNode>();
创建一个HashSet用于存储链表节点
ListNode temp = headA; while (temp != null) {visited.add(temp);temp = temp.next; }
遍历链表A,将所有节点添加到HashSet中
temp = headB; while (temp != null) {if (visited.contains(temp)) {return temp;}temp = temp.next; }
遍历链表B,检查每个节点是否存在于HashSet中
如果存在,则立即返回该节点(第一个相交节点)
return null;
如果遍历完链表B都没有找到相交节点,返回null
复杂度分析
时间复杂度:O(m+n),其中m和n分别是两个链表的长度
空间复杂度:O(m),需要存储链表A的所有节点
其他解法
这种方法虽然直观,但需要额外空间。还有两种更优的空间O(1)解法:
双指针法:
计算两个链表的长度
让长链表的指针先移动长度差步
然后两个指针同步前进,相遇点即为交点
环形检测法:
将链表A的尾节点连接到链表B的头节点
使用快慢指针检测环的起点,即为交点
最后需要恢复链表结构
边界情况
两个链表都为空
一个链表为空
两个链表不相交
两个链表完全重合
交点在链表头部或尾部
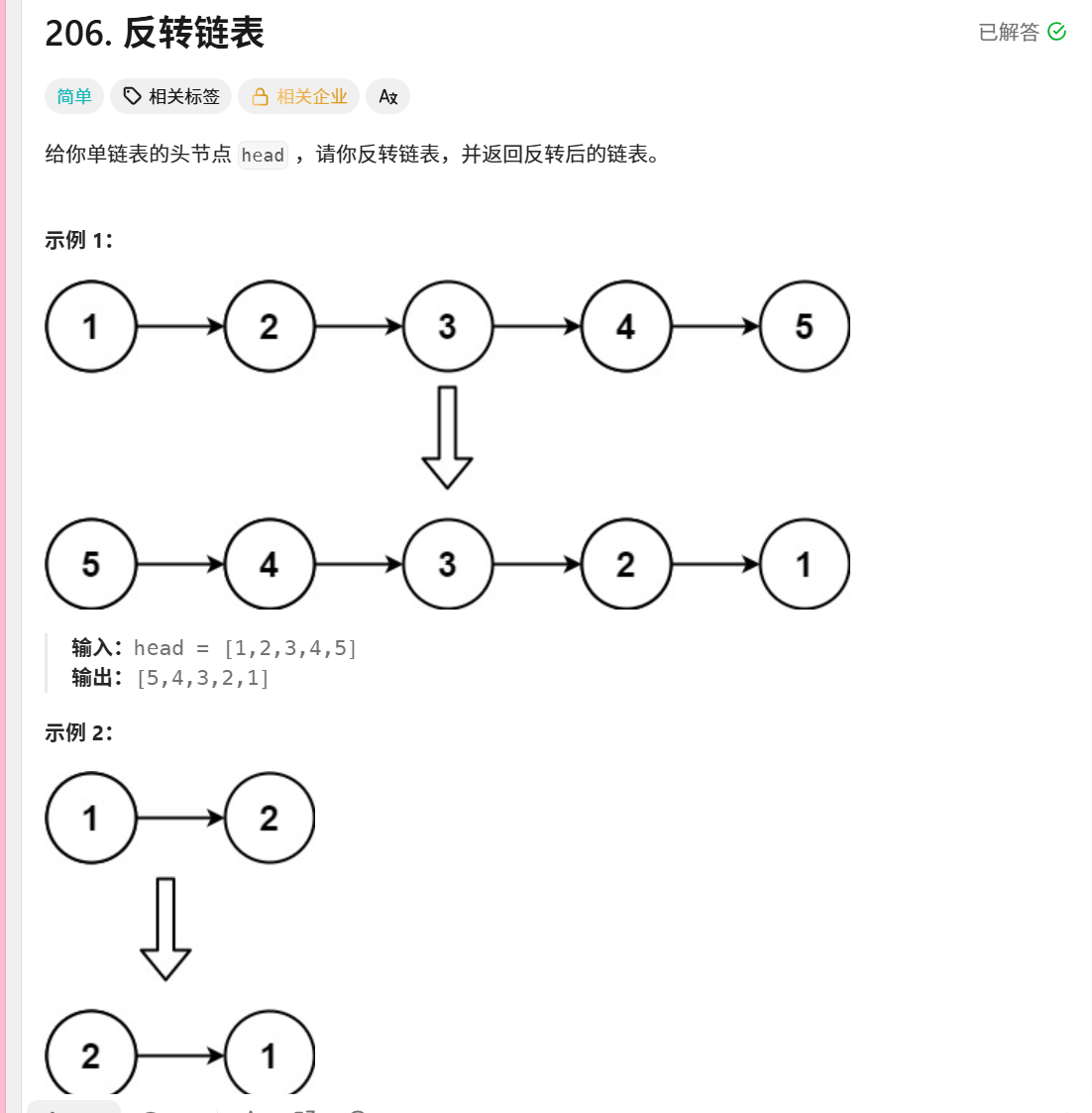
206. 反转链表

/*** Definition for singly-linked list.* public class ListNode {* int val;* ListNode next;* ListNode() {}* ListNode(int val) { this.val = val; }* ListNode(int val, ListNode next) { this.val = val; this.next = next; }* }*/
class Solution {/*** 反转单链表* @param head 原链表的头节点* @return 反转后新链表的头节点*/public ListNode reverseList(ListNode head) {// prev指针用于记录前一个节点,初始为null(因为反转后原头节点将指向null)ListNode prev = null;// curr指针用于遍历链表,初始指向原链表头节点ListNode curr = head;// 遍历链表直到当前节点为null(到达链表尾部)while (curr != null) {// 1. 先保存当前节点的下一个节点(否则修改指针后会丢失)ListNode next = curr.next;// 2. 反转指针方向:当前节点的next指向前一个节点curr.next = prev;// 3. 移动prev指针到当前节点(为下一次迭代做准备)prev = curr;// 4. 移动curr指针到之前保存的下一个节点curr = next;}// 循环结束时,prev指向原链表的最后一个节点,即新链表的头节点return prev;}
}算法图解
假设原始链表为:1 → 2 → 3 → 4 → null
执行过程:
初始状态:prev = null, curr = 1
第一次迭代后:null ← 1 2 → 3 → 4 → null
第二次迭代后:null ← 1 ← 2 3 → 4 → null
第三次迭代后:null ← 1 ← 2 ← 3 4 → null
第四次迭代后:null ← 1 ← 2 ← 3 ← 4
最终返回节点4作为新链表的头节点
关键点说明
三指针技术:
prev:记录前一个节点
curr:当前处理节点
next:临时保存下一个节点指针操作顺序:
必须先保存
next = curr.next,否则反转后会丢失后续链表然后才能修改
curr.next指向最后移动
prev和curr指针终止条件:
当
curr == null时循环结束此时
prev指向原链表的最后一个节点(新链表的头节点)边界情况处理:
空链表(head == null):直接返回null
单节点链表:自动正确处理
复杂度分析
时间复杂度:O(n),只需遍历链表一次
空间复杂度:O(1),只使用了固定数量的指针变量
234. 回文链表

/*** Definition for singly-linked list.* public class ListNode {* int val;* ListNode next;* ListNode() {}* ListNode(int val) { this.val = val; }* ListNode(int val, ListNode next) { this.val = val; this.next = next; }* }*/
class Solution {public boolean isPalindrome(ListNode head) {ListNode temp=head;List<Integer> vals = new ArrayList<Integer>();while(temp!=null){vals.add(temp.val);temp=temp.next;}int left=0;int length=vals.size();int right=length-1;while(left<right){if(vals.get(left)!=vals.get(right)){return false;}left++;right--;}return true;}
}算法分析
方法思路
存储阶段:将链表所有节点的值按顺序存入一个ArrayList
验证阶段:使用双指针法,从列表两端向中间比较元素是否对称
时间复杂度
O(n):需要完整遍历链表两次(一次存储,一次比较)
其中n是链表的长度
空间复杂度
O(n):需要使用额外空间存储所有节点的值
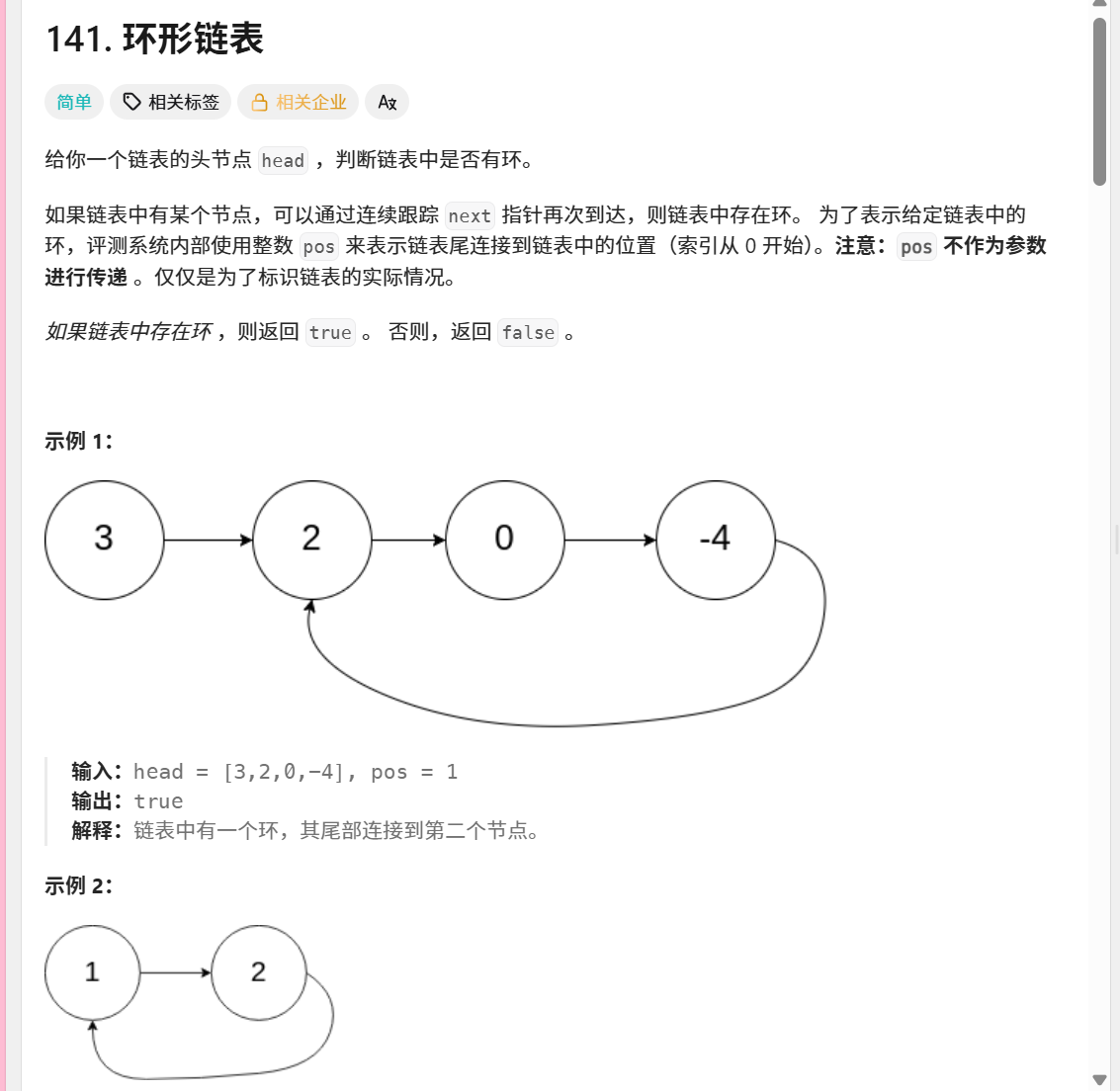
141. 环形链表

/*** Definition for singly-linked list.* class ListNode {* int val;* ListNode next;* ListNode(int x) {* val = x;* next = null;* }* }*/
public class Solution {/*** 检测链表是否有环* @param head 链表头节点* @return 如果链表有环返回true,否则返回false*/public boolean hasCycle(ListNode head) {// 处理边界情况:空链表或单节点无环if (head == null || head.next == null) {return false;}// 初始化快慢指针ListNode slow = head; // 慢指针每次走1步ListNode fast = head.next; // 快指针每次走2步// 当快慢指针不相遇时继续循环while (slow != fast) {// 如果快指针到达链表末尾,说明无环if (fast == null || fast.next == null) {return false;}// 移动指针slow = slow.next; // 慢指针走1步fast = fast.next.next; // 快指针走2步}// 快慢指针相遇,说明有环return true;}
}算法原理(Floyd判圈算法)
核心思想
使用两个指针,一个慢指针(每次移动1步),一个快指针(每次移动2步)
如果链表无环,快指针会先到达末尾(null)
如果链表有环,快指针最终会追上慢指针(相遇)
为什么这样能工作
无环情况:快指针会先到达链表末尾(null)
有环情况:
快指针每次比慢指针多走1步
经过若干步后,快指针会绕环一圈追上慢指针
可以证明最多需要O(n)时间就能检测出环
关键点解析
指针初始化:
慢指针
slow从head开始快指针
fast从head.next开始(避免第一次循环就满足slow==fast)循环条件:
当
slow != fast时继续循环如果相等则跳出循环,返回true(有环)
终止条件检查:
检查
fast == null || fast.next == null因为fast走得快,只需要检查fast是否到末尾
指针移动:
慢指针每次移动1步:
slow = slow.next快指针每次移动2步:
fast = fast.next.next复杂度分析
时间复杂度:O(n)
无环情况:快指针到达末尾,最多n/2步
有环情况:慢指针最多走一圈就会被快指针追上
空间复杂度:O(1)
只使用了两个额外指针,常数空间
边界情况处理
空链表:直接返回false
单节点链表:直接返回false(除非自环,但题目通常不考虑)
大环/小环:算法都能正确处理
环在头部/尾部:都能正确检测
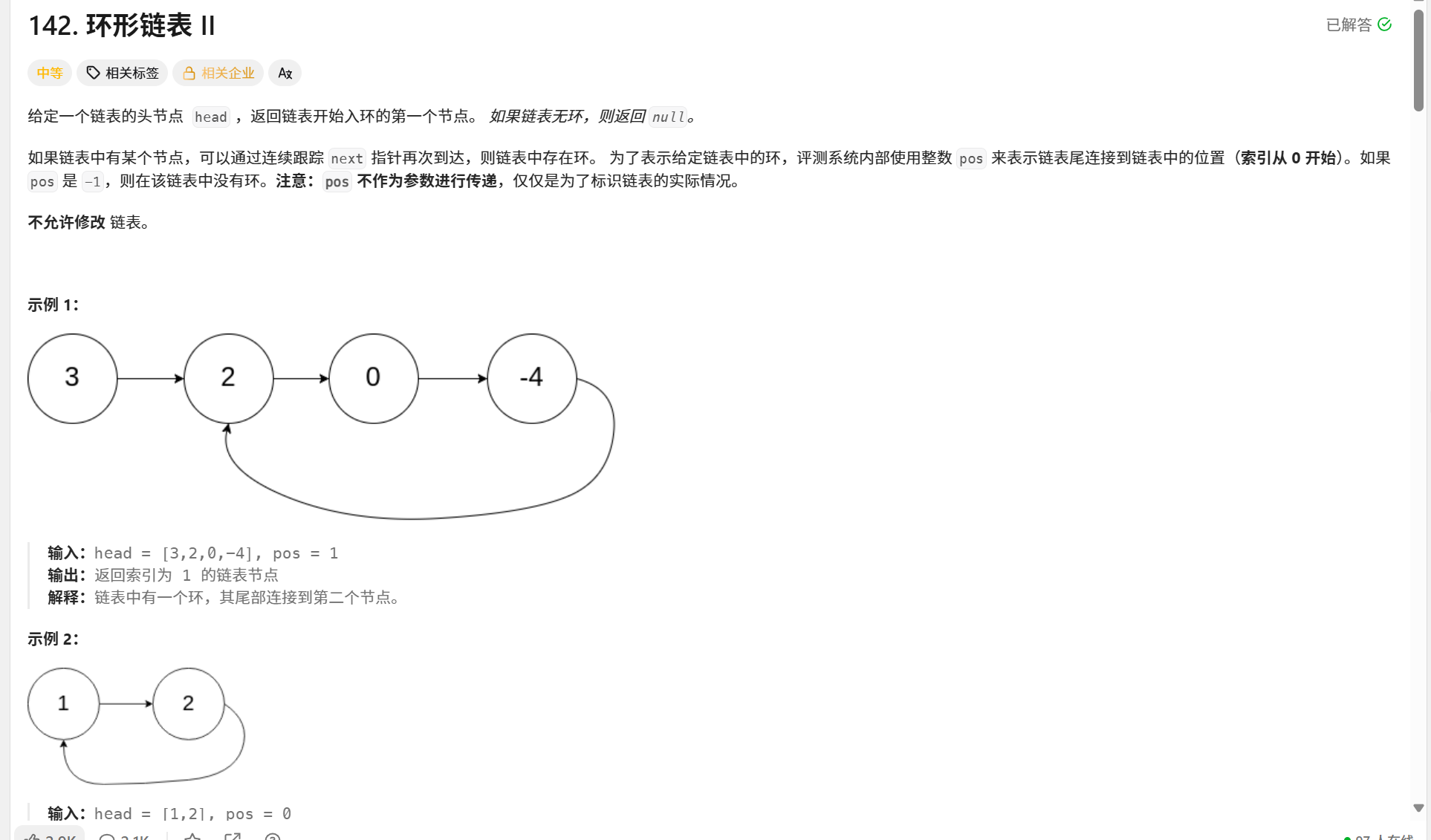
142. 环形链表 II

/*** Definition for singly-linked list.* class ListNode {* int val;* ListNode next;* ListNode(int x) {* val = x;* next = null;* }* }*/
public class Solution {public ListNode detectCycle(ListNode head) {if(head==null){return null;}ListNode slow = head; // 慢指针ListNode fast = head; // 快指针while(fast!=null){slow=slow.next;if(fast.next!=null){fast=fast.next.next;}else{return null;}if(slow==fast){ListNode temp=head;while(temp!=slow){temp=temp.next;slow=slow.next;}return temp;}}return null;}
}算法原理(Floyd判圈算法的扩展)
第一阶段:检测环的存在
快指针每次移动2步,慢指针每次移动1步
如果快指针遇到null,说明链表无环
如果快慢指针相遇,说明链表有环
第二阶段:确定环的起点
当快慢指针相遇后,将一个指针(temp)重新指向链表头部
temp和slow指针每次都移动1步
当它们再次相遇时,相遇点就是环的起点
数学证明
设:
链表头到环起点的距离为a
环起点到相遇点的距离为b
相遇点回到环起点的距离为c
环的长度为L = b + c
当快慢指针相遇时:
慢指针走的距离:a + b
快指针走的距离:a + b + k*L (k为快指针绕环的圈数)
因为快指针速度是慢指针的2倍:
2(a + b) = a + b + kL
=> a + b = kL
=> a = k*L - b = (k-1)*L + c这意味着:从链表头走a步,等于从相遇点走c步加上整数倍的环长。因此,两个指针分别从头节点和相遇点出发,以相同速度前进,必将在环起点相遇。
复杂度分析
时间复杂度:O(n)
第一阶段最多需要O(n)时间检测环
第二阶段最多需要O(n)时间找到环起点
空间复杂度:O(1)
只使用了固定数量的指针变量
边界情况处理
空链表:直接返回null
单节点无环:快指针会走到null
单节点自环:能正确检测并返回该节点
环在头部:能正确返回头节点
环在尾部:能正确返回环起点



(下篇))
 :哈希表(Hash Table)中的一个关键性能指标)
原理)




Digit Recognizer 手写数字识别)








