温馨提示：
本篇文章已同步至"AI专题精讲" PPO：近端策略优化算法

摘要

我们提出了一类新的用于强化学习的 policy gradient 方法，该方法在与环境交互以采样数据和使用随机梯度上升优化一个“代理”目标函数之间交替进行。与标准的 policy gradient 方法每个数据样本只进行一次梯度更新不同，我们提出了一种新颖的目标函数，使得可以对同一批数据进行多个 epoch 的小批量更新。这些新方法被称为 Proximal Policy Optimization（PPO），它们继承了 Trust Region Policy Optimization（TRPO） 的一些优势，但实现更简单、适用范围更广，并且在经验上具有更好的样本效率。我们的实验在一系列基准任务上对 PPO 进行了测试，包括模拟的机器人运动和 Atari 游戏，结果表明 PPO 在所有在线 policy gradient 方法中表现更优，整体上在样本效率、简单性和运行时间之间达成了良好的平衡。

1 引言

近年来，已经提出了多种使用神经网络函数逼近器进行强化学习的方法。主要的候选方案包括 Deep Q-learning [Mni+15]、“vanilla” policy gradient 方法 [Mni+16] 以及 Trust Region / Natural Policy Gradient 方法 [Sch+15b]。不过，目前在开发一种具备可扩展性（适用于大型模型与并行实现）、数据高效性以及鲁棒性（即在多种问题中无需超参数调节即可成功）的算法方面，仍有改进空间。Q-learning（带函数逼近）在许多简单问题上都会失败¹，且机制尚不清楚；vanilla policy gradient 方法的数据效率和鲁棒性都较差；而 TRPO相对复杂，且不兼容某些结构中存在噪声（如 dropout）或参数共享（比如策略与价值函数间或与辅助任务共享参数）。

本文旨在通过引入一种仅依赖一阶优化的算法，来实现 TRPO 所具有的数据效率与可靠性。我们提出了一个带有截断概率比的全新目标函数，它构成了策略性能的悲观估计（即下界）。为了优化策略，我们在从策略中采样数据和在采样数据上进行多个 epoch 优化之间进行交替。我们的实验比较了不同版本的代理目标函数的性能，发现使用截断概率比的版本表现最佳。我们还将 PPO 与文献中的多种算法进行了对比。在连续控制任务中，它优于我们比较的其他算法；在 Atari 游戏中，其样本效率显著超过 A2C，且与 ACER 表现相当，但实现更为简单。

2 背景：策略优化

2.1 Policy Gradient 方法

Policy Gradient 方法通过估计策略梯度，并将其代入随机梯度上升算法来实现优化。最常用的梯度估计器形式如下：

$g^=E^t[∇θlog⁡πθ(at∣st)A^t](1)\hat{g} = \hat{\mathbb{E}}_t\left[\nabla_\theta \log \pi_\theta(a_t \mid s_t) \hat{A}_t\right] \quad(1)$

其中， $πθ\pi_\theta$ 是一个随机策略， $A^t\hat{A}_t$ 是在时间步 $t$ 的 Advantage Function 的估计值。这里的期望 $E^t[…]\hat{\mathbb{E}}_t[\dots]$ 表示在有限样本批次上的经验平均，该算法在采样和优化之间交替进行。

在使用自动微分软件的实现中，策略梯度估计器是通过构建一个目标函数来获得的，该目标函数的梯度即为策略梯度估计器 $g^\hat{g}$ ；该目标函数为：

$LPG(θ)=E^t[log⁡πθ(at∣st)A^t](2)\begin{array} { r } { L ^ { P G } ( \theta ) = \hat { \mathbb { E } } _ { t } \Bigl [ \log \pi _ { \theta } ( a _ { t } \mid s _ { t } ) \hat { A } _ { t } \Bigr ] } \end{array}\quad(2)$

虽然在相同轨迹上对该损失 $L^{PG}$ 执行多步优化听起来是有吸引力的，但这种做法缺乏理论支撑，且在实践中常常会导致策略更新过大，从而产生破坏性效果（见第6.1节；相关结果未展示，但与“无剪切或惩罚”设定下的结果相似或更差）。

2.2 Trust Region 方法

在 TRPO [Sch+15b] 中，目标函数（即“代理”目标函数）在策略更新幅度受到约束的条件下被最大化。具体如下：

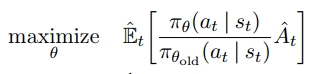
在这里插入图片描述

满足以下约束条件：

$E^t[KL[πθold(⋅∣st),πθ(⋅∣st)]]≤δ(4)\hat{\mathbb{E}}_t \left[ \text{KL}[\pi_{\theta_{\text{old}}}(\cdot \mid s_t), \pi_\theta(\cdot \mid s_t)] \right] \leq \delta \quad(4)$

这里， $θold\theta_{\text{old}}$ 是更新之前的策略参数向量。这个问题可以通过共轭梯度算法（conjugate gradient algorithm）高效地近似求解，方法是在目标函数上做线性近似、在约束项上做二次近似。

TRPO 的理论实际上建议使用惩罚项替代约束，即求解如下的无约束优化问题：

$maximize⁡θE^t[πθ(at∣st)πθold(at∣st)A^t−βKL⁡[πθold(⋅∣st),πθ(⋅∣st)]](5)\operatorname* { m a x i m i z e } _ { \theta } \hat { \mathbb { E } } _ { t } \left[ \frac { \pi _ { \theta } ( a _ { t } \mid s _ { t } ) } { \pi _ { \theta _ { \mathrm { o l d } } } ( a _ { t } \mid s _ { t } ) } \hat { A } _ { t } - \beta \operatorname { K L } [ \pi _ { \theta _ { \mathrm { o l d } } } ( \cdot \mid s _ { t } ) , \pi _ { \theta } ( \cdot \mid s _ { t } ) ] \right]\quad(5)$

其中 $β\beta$ 是某个系数。这一做法的理论基础是，某种代理目标（其对状态取最大 KL 而非平均）构成了策略 $π\pi$ 表现的下界（即悲观估计）。TRPO 之所以采用硬约束而不是惩罚项，是因为很难选择一个在不同问题中都能表现良好的固定 $β\beta$ 值——甚至在同一个问题中，随着学习过程的推进，问题特性也会发生变化。因此，为了实现我们提出的目标：使用一阶优化算法复现 TRPO 的单调性能改进，实验表明，仅仅使用固定惩罚系数 $β\beta$ 并用 SGD 优化带惩罚项的目标函数（公式 (5)）是不够的；还需要额外的修改。

3 Clipped Surrogate Objective

令 $rt(θ)r_t(\theta)$ 表示概率比：

$r(θold)=1。r_t(\theta) = \frac{\pi_\theta(a_t \mid s_t)}{\pi_{\theta_{\mathrm{old}}}(a_t \mid s_t)}，\quad \text{因此}~r(\theta_{\mathrm{old}}) = 1。$

TRPO 最大化一个“代理”目标函数：

$LCPI(θ)=E^t[πθ(at∣st)πθold(at∣st)A^t]=E^t[rt(θ)A^t](6)L^{CPI}(\theta) = \hat{\mathbb{E}}_t\left[ \frac{\pi_\theta(a_t \mid s_t)}{\pi_{\theta_{\mathrm{old}}}(a_t \mid s_t)} \hat{A}_t \right] = \hat{\mathbb{E}}_t\left[ r_t(\theta)\, \hat{A}_t \right] \quad(6)$

上标 CPI 指的是 conservative policy iteration（保守策略迭代）[KL02]，该目标函数即源自于此。如果没有约束，直接最大化 $L^{CPI}$ 会导致过大的策略更新。因此，我们考虑如何修改该目标函数，以惩罚使 $rt(θ)r_t(\theta)$ 偏离 1 的策略变动。

我们提出的主要目标函数如下：

$LCLIP(θ)=E^t[min⁡(rt(θ)A^t,clip⁡(rt(θ),1−ϵ,1+ϵ)A^t)](7)L^{CLIP}(\theta) = \hat{\mathbb{E}}_t\left[ \min\left( r_t(\theta) \hat{A}_t, \operatorname{clip}(r_t(\theta), 1 - \epsilon, 1 + \epsilon)\, \hat{A}_t \right) \right] \quad(7)$

其中 $ϵ\epsilon$ 是一个超参数，例如 $ϵ=0.2\epsilon = 0.2$ 。

该目标函数的动机如下：min 内的第一个项即为 $L^{CPI}$ ；第二项 clip（ $rt(θ),1−ϵ,1+ϵr_t(\theta), 1 - \epsilon, 1 + \epsilon$ ）对概率比进行截断，从而移除了将 $r_t$ 移出区间 $\epsilon, 1 + \epsilon]$ 的动机。最终我们取截断前后的最小值，因此最终目标函数是未截断目标的一个下界（即悲观估计）。该方法只在改变概率比会提升目标函数时忽略这种改变，而当其会使目标变差时就保留这种惩罚。注意，在 $θold\theta_{\mathrm{old}}$ 附近的一阶近似下， $LCLIP(θ)=LCPI(θ)L^{CLIP}(\theta) = L^{CPI}(\theta)$ （即 $r = 1$ 时），然而当 $θ\theta$ 远离 $θold\theta_{\mathrm{old}}$ 时，两者将会不同。图 1 绘制了 $L^{CLIP}$ 中单个 $t$ 项的图像；注意，概率比 $r$ 在 $\epsilon$ 或 $\epsilon$ 处被截断，具体取决于优势值是正还是负。
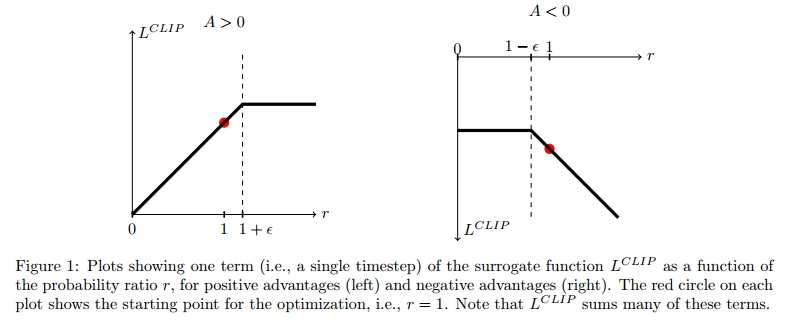
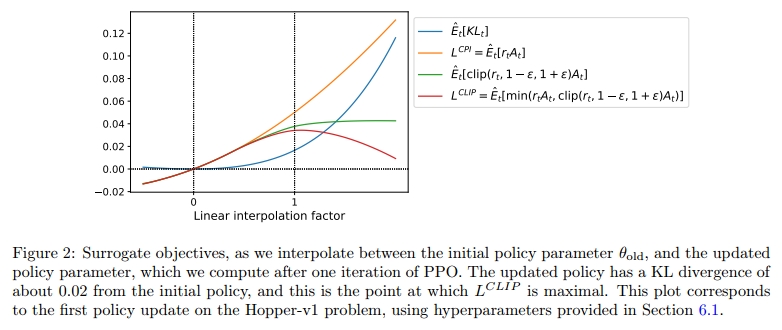
在这里插入图片描述

图 2 提供了关于代理目标 $L^{CLIP}$ 的另一种直观理解。它展示了在策略更新方向上插值得到的多个目标函数是如何变化的，该更新方向是通过 proximal policy optimization（我们即将介绍的算法）在一个连续控制问题中得到的。我们可以看到， $L^{CLIP}$ 是 $L^{CPI}$ 的一个下界，并对策略更新过大的情况施加了惩罚。
在这里插入图片描述

4 自适应 KL 惩罚系数

另一种方法可以作为 clipped surrogate objective 的替代方案，或者与其结合使用，即对 KL 散度施加惩罚，并自适应地调整惩罚系数，以便在每次策略更新时达到某个目标 KL 散度 $dtargd_{\text{targ}}$ 。在我们的实验中，我们发现 KL 惩罚的表现不如 clipped surrogate objective，然而我们仍在此处包括这一方法，因为它是一个重要的基线方法。

在该算法最简单的实现中，每次策略更新执行以下步骤：

使用多个 epoch 的小批量 SGD，优化带 KL 惩罚的目标函数：

$LKLPEN(θ)=E^t[πθ(at∣st)πθold(at∣st)A^t−βKL[πθold(⋅∣st),πθ(⋅∣st)]](8)L^{KLPEN}(\theta) = \hat{\mathbb{E}}_t \left[ \frac{\pi_\theta(a_t \mid s_t)}{\pi_{\theta_{\text{old}}}(a_t \mid s_t)} \hat{A}_t - \beta \, \mathrm{KL}[\pi_{\theta_{\text{old}}}(\cdot \mid s_t), \pi_\theta(\cdot \mid s_t)] \right] \quad(8)$
计算 $d=E^t[KL[πθold(⋅∣st),πθ(⋅∣st)]]d = \hat{\mathbb{E}}_t[\mathrm{KL}[\pi_{\theta_{\text{old}}}(\cdot \mid s_t), \pi_\theta(\cdot \mid s_t)]]$

– 如果 $\frac{d_{\text{targ}}}{1.5}$ ，则令 $β←β/2\beta \leftarrow \beta / 2$

– 如果 $d_{\text{targ}} \times 1.5$ ，则令 $β←β×2\beta \leftarrow \beta \times 2$

更新后的 $β\beta$ 会在下一次策略更新中使用。在该机制下，我们偶尔会看到 KL 散度与 $dtargd_{\text{targ}}$ 相差较大的策略更新，但这类情况比较罕见，且 $β\beta$ 会快速调整。上述参数 1.5 和 2 是启发式选择的，但该算法对它们并不敏感。初始值 $β\beta$ 是另一个超参数，但在实践中影响不大，因为算法能迅速调整它。