目录
1. 岛屿数量
1.1 题目解析
1.2 解法
1.3 代码实现
2. 岛屿的最大面积
2.1 题目解析
2.2 解法
2.3 代码实现
1. 岛屿数量
https://leetcode.cn/problems/number-of-islands/
给你一个由 '1'(陆地)和 '0'(水)组成的的二维网格,请你计算网格中岛屿的数量。
岛屿总是被水包围,并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。
此外,你可以假设该网格的四条边均被水包围。
示例 1:
输入:grid = [['1','1','1','1','0'],['1','1','0','1','0'],['1','1','0','0','0'],['0','0','0','0','0'] ] 输出:1
示例 2:
输入:grid = [['1','1','0','0','0'],['1','1','0','0','0'],['0','0','1','0','0'],['0','0','0','1','1'] ] 输出:3
提示:
m == grid.lengthn == grid[i].length1 <= m, n <= 300grid[i][j]的值为'0'或'1'
1.1 题目解析
题目本质
-
在一个 m×n 的 0/1 网格上,统计由上下左右连通的“1”块的个数;本质是“连通分量计数(四联通)”。
常规解法
-
朴素想法:对每个为 ‘1’ 的格子启动一次遍历,把与之相连的 ‘1’ 都标记掉,然后计数 +1。遍历可用 DFS 或 BFS。
问题分析
-
如果不做“访问标记(vis)”,同一块岛屿会被重复启动遍历 → 重复计数/超时。
-
如果标记时机不当(入队后不立刻标记),同一坐标会被多次入队 → 队列暴涨。
-
边界获取不当(先取 grid[0].length 再判断空矩阵)会 NPE。
-
复杂度:每格最多访问一次,理想是 O(mn);只要保证“入队(或递归)前标记”为时机,就不会退化。
思路转折
-
要高效、且不重算:
-
必须维护 vis[m][n] 访问标记;
-
必须把标记动作放在“入队/入栈前”;
-
必须只在遇到“未访问的 ‘1’”时启动一次 BFS/DFS,并在启动点处给计数器 +1。
-
-
这样“每个格子至多被处理一次”,时间 O(mn)、空间 O(mn)。
1.2 解法
算法思想
-
遍历整个网格;每当遇到 grid[i][j]=='1' && !vis[i][j]:
-
启动一轮 BFS;
-
BFS 中用队列弹出当前格,向四邻扩展,对满足边界且为 ‘1’ 且未访问的坐标:先标记 vis=true,再入队;
-
该轮 BFS 结束后,说明整块岛屿已被吞并,计数 ret++。
-
i)初始化
-
m = grid.length;若 m==0 直接返回 0。
-
n = grid[0].length;vis = new boolean[m][n];ret = 0。
ii)扫描网格
-
双层循环 (i,j);当 grid[i][j]=='1' && !vis[i][j] 时,启动 BFS(i,j)。
iii)BFS 过程
-
队列入起点 (si,sj),立刻标记 vis[si][sj]=true。
-
不断出队 (a,b),向四方向 (a+dx[k], b+dy[k]) 扩展;满足:
-
在边界内、
-
未访问、
-
且为 ‘1’
→ 先标记再入队。 -
队列清空即该岛处理完毕,ret++。
-
iiii)返回 ret。
易错点
-
n = grid[0].length 必须放在 m==0 判空之后,否则空矩阵会 NPE。
-
if (grid[i][j]=='1' && !vis[i][j]) 中的 !vis[i][j] 一开始当然都是 true,但第一轮 BFS 会把整块岛都标记为
true,后续再遇到同岛格子就不会重复启动 BFS。 -
标记时机要在入队前/时,否则同一坐标可能被多次入队。
-
只统计“第一次发现这块岛”的那一刻(启动 BFS 时)的一次 ret++
-
注意字符比较用
'1',不要写成1。 -
四方向遍历下标不要写错。
-
不要重复无意义的标记(出队后再次 vis[a][b]=true 属于冗余)。
1.3 代码实现
import java.util.*;class Solution {int[] dx = {0, 0, 1, -1};int[] dy = {1, -1, 0, 0};int m, n;Queue<int[]> q = new LinkedList<>();boolean[][] vis;int ret;public int numIslands(char[][] grid) {m = grid.length;if (m == 0) return 0; // 先判空,再取 nn = grid[0].length;vis = new boolean[m][n];ret = 0;for (int i = 0; i < m; i++) {for (int j = 0; j < n; j++) {if (grid[i][j] == '1' && !vis[i][j]) {bfs(grid, i, j); // 一次 BFS 吞并一整块岛}}}return ret;}// BFS:以 (si, sj) 为起点吞并整块岛屿public void bfs(char[][] grid, int si, int sj) {q.clear(); // 成员队列:显式清空更稳妥q.offer(new int[]{si, sj});vis[si][sj] = true; // 入队前/时标记,避免重复入队while (!q.isEmpty()) {int[] cur = q.poll();int a = cur[0], b = cur[1];for (int k = 0; k < 4; k++) {int x = a + dx[k], y = b + dy[k];if (x >= 0 && x < m && y >= 0 && y < n&& !vis[x][y] && grid[x][y] == '1') {vis[x][y] = true; // 先标记,再入队q.offer(new int[]{x, y});}}}ret++; // 本轮 BFS 结束 → 发现了一座岛}
}
复杂度分析
-
时间复杂度:O(m·n),每个格子最多被入队/出队一次,四邻检查是常数。
-
空间复杂度:O(m·n),主要在 vis;队列最坏可能装下整层边界上的若干格子,但受 O(mn) 上界。
2. 岛屿的最大面积
https://leetcode.cn/problems/max-area-of-island/
给你一个大小为 m x n 的二进制矩阵 grid 。
岛屿 是由一些相邻的 1 (代表土地) 构成的组合,这里的「相邻」要求两个 1 必须在 水平或者竖直的四个方向上 相邻。你可以假设 grid 的四个边缘都被 0(代表水)包围着。
岛屿的面积是岛上值为 1 的单元格的数目。
计算并返回 grid 中最大的岛屿面积。如果没有岛屿,则返回面积为 0 。
示例 1:
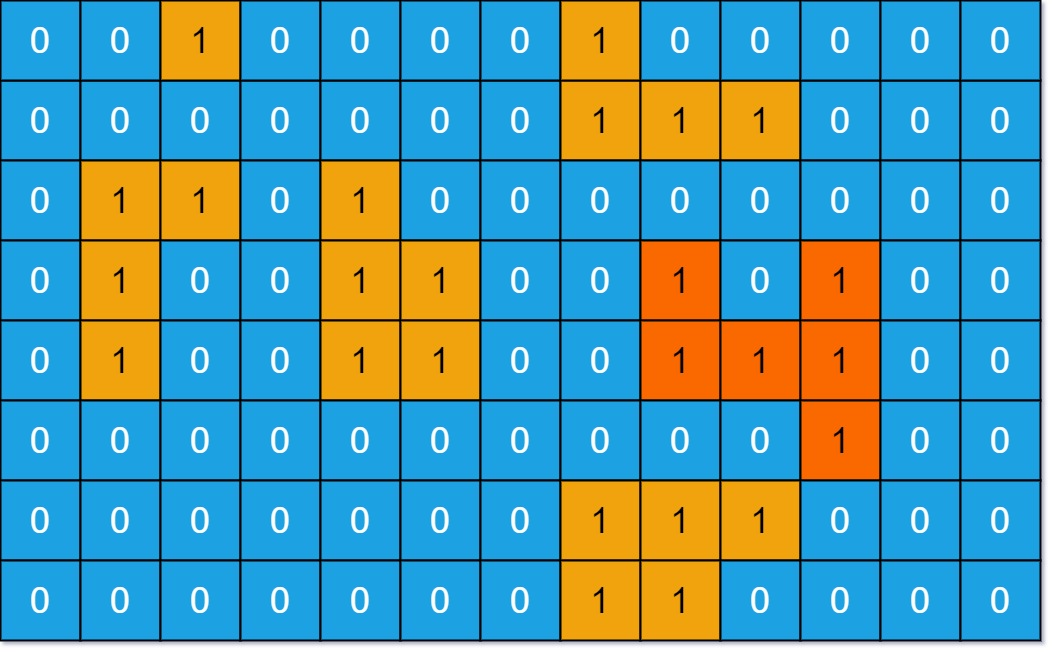
输入:grid = [[0,0,1,0,0,0,0,1,0,0,0,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,1,1,0,1,0,0,0,0,0,0,0,0],[0,1,0,0,1,1,0,0,1,0,1,0,0],[0,1,0,0,1,1,0,0,1,1,1,0,0],[0,0,0,0,0,0,0,0,0,0,1,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,0,0,0,0,0,0,1,1,0,0,0,0]] 输出:6 解释:答案不应该是11,因为岛屿只能包含水平或垂直这四个方向上的1。
示例 2:
输入:grid = [[0,0,0,0,0,0,0,0]] 输出:0
提示:
m == grid.lengthn == grid[i].length1 <= m, n <= 50grid[i][j]为0或1
2.1 题目解析
题目本质
-
在 m×n 的二值矩阵中,按四联通把为 1 的格子聚合成若干连通分量,返回所有分量的最大节点数,也就是最大岛屿面积。
常规解法
-
线性扫描整张表,每当遇到未访问的 1,就从该点出发做一次搜索,把整座岛吞并,并统计面积。可用 BFS 或 DFS。
问题分析
-
如果不做访问标记,同一岛会被多次重复遍历,时间爆炸。
-
如果标记时机晚(入队后才标记,甚至出队后才标记),同一坐标可能被多次入队,导致队列暴涨。
-
如果把面积计数放在“发现邻居”时,会漏掉起点,得到 N−1 而不是 N。
-
判空顺序不当会空指针,例如先取 grid[0].length 再判断 m 是否为 0。
-
复杂度目标是 O(mn),只要保证每格最多被访问一次即可。
思路转折
-
要想稳定 O(mn):
-
需要全局 vis 数组去重。
-
需要在入队之前标记 vis,保证每格最多入队一次。
-
需要把面积计数与“访问到一个新格子”绑定,最简单是出队时加一。
-
只在遇到 grid[i][j] == 1 且未访问时启动一次搜索,吞并整座岛并更新答案。
-
2.2 解法
算法思想
-
双层循环扫描网格,遇到未访问的 1 启动 BFS。
-
BFS 初始化把起点入队并立刻标记已访问。
-
循环弹出队头,面积加一,向四个方向扩展,把满足边界、为 1、未访问的邻居先标记后入队。
-
本轮队列清空即整座岛处理完毕,用该岛面积更新全局最大值。
i)初始化
-
m = grid.length,若 m == 0 直接返回 0。
-
n = grid[0].length,初始化 vis[m][n] 为 false。
-
准备一个整型答案 ret 保存最大面积。
ii)扫描
-
双层循环 i, j。
-
当且仅当 grid[i][j] == 1 且 vis[i][j] 为 false 时,启动 BFS(i, j)。
iii)BFS 细节
-
入队起点并立刻标记 vis[si][sj] = true。
-
while 队列非空:
-
弹出一个格子,面积加一。
-
四方向扩展,满足边界、为 1、未访问的邻居先标记再入队。
-
-
返回本轮面积。
iiii)更新答案
-
ret = max(ret, 本轮面积)。
iiiii)返回 ret
易错点
-
判空顺序:必须先判断 m 是否为 0,再读取 grid[0].length。
-
标记时机:必须在入队之前标记,防止同一坐标被多次入队。
-
面积计数位置:推荐在出队时加一,这样每访问一个格子恰好计一次;如果坚持在“发现邻居”时计数,必须把起点先计入,否则会少一。
-
邻居入队坐标:入队的是邻居 (x, y),不要误把起点 (si, sj) 重新塞回队列。
-
只考虑四联通,不能把对角线当作连通。
-
类型与比较:本题 grid 是 int[][],比较用 1 与 0;与 char[][] 的版本不要混用。
2.3 代码实现
import java.util.*;class Solution {Queue<int[]> q = new LinkedList<>(); // 成员队列,BFS 开始时清空更稳妥int m, n;boolean[][] vis;int[] dx = {0, 0, 1, -1};int[] dy = {1, -1, 0, 0};public int maxAreaOfIsland(int[][] grid) {m = grid.length;if (m == 0) return 0; // 先判空,避免 NPEn = grid[0].length;vis = new boolean[m][n];int ret = 0, cur = 0;for (int i = 0; i < m; i++) {for (int j = 0; j < n; j++) {if (grid[i][j] == 1 && !vis[i][j]) {cur = 0; // 可有可无,这里保持你的风格int tmp = bfs(grid, i, j, cur); // BFS 返回本岛面积ret = Math.max(ret, tmp);}}}return ret;}// BFS 吞并以 (si, sj) 为起点的整座岛,返回其面积public int bfs(int[][] grid, int si, int sj, int cur) {q.clear(); // 成员队列,使用前先清空q.offer(new int[]{si, sj});vis[si][sj] = true;while (!q.isEmpty()) {int[] num = q.poll();int a = num[0], b = num[1];cur++; // 出队即计数,保证每格计一次for (int i = 0; i < 4; i++) {int x = a + dx[i], y = b + dy[i];if (x >= 0 && x < m && y >= 0 && y < n&& grid[x][y] == 1 && !vis[x][y]) {vis[x][y] = true; // 入队前标记q.offer(new int[]{x, y}); // 入队邻居坐标}}}return cur;}
}
复杂度分析
-
时间复杂度:O(mn),每个格子最多被访问一次,四邻检查是常数。
-
空间复杂度:O(mn),主要为 vis;队列最坏情况下也不超过 O(mn)。






![LINUX913 shell:set ip [lindex $argv 0],\r,send_user,spawn ssh root@ip “cat “](http://pic.xiahunao.cn/LINUX913 shell:set ip [lindex $argv 0],\r,send_user,spawn ssh root@ip “cat “)



 + delta)` 而不是除以图像尺寸?)

)






