在深度学习的世界里，神经网络的训练常常充满了挑战。从复杂的梯度问题到漫长的收敛过程，每一个环节都可能成为阻碍我们前进的绊脚石。

而今天，我们要深入探讨的 $BatchNormalization$（批量归一化），正是这样一种能够显著提升训练效率和模型性能的“神技”。

那么，$BatchNormalization$ 究竟是如何工作的？它背后的数学原理又是什么？

接下来，就让我们一起揭开它的神秘面纱。

一、数据归一化的数学意义

在正式进入Batch Normalization之前，我们先来聊聊数据归一化。

归一化，顾名思义，就是将数据缩放到一个统一的范围，让它们在同一个尺度上“公平竞争”。

想象一下，如果你有一个数据集，其中一部分特征的数值范围是0到1，而另一部分特征的数值范围是0到1000。 那么在训练过程中，数值范围更大的特征可能会“淹没”其他特征，导致模型对它们过度依赖，而忽略了其他重要的信息。

图1. 归一化处理

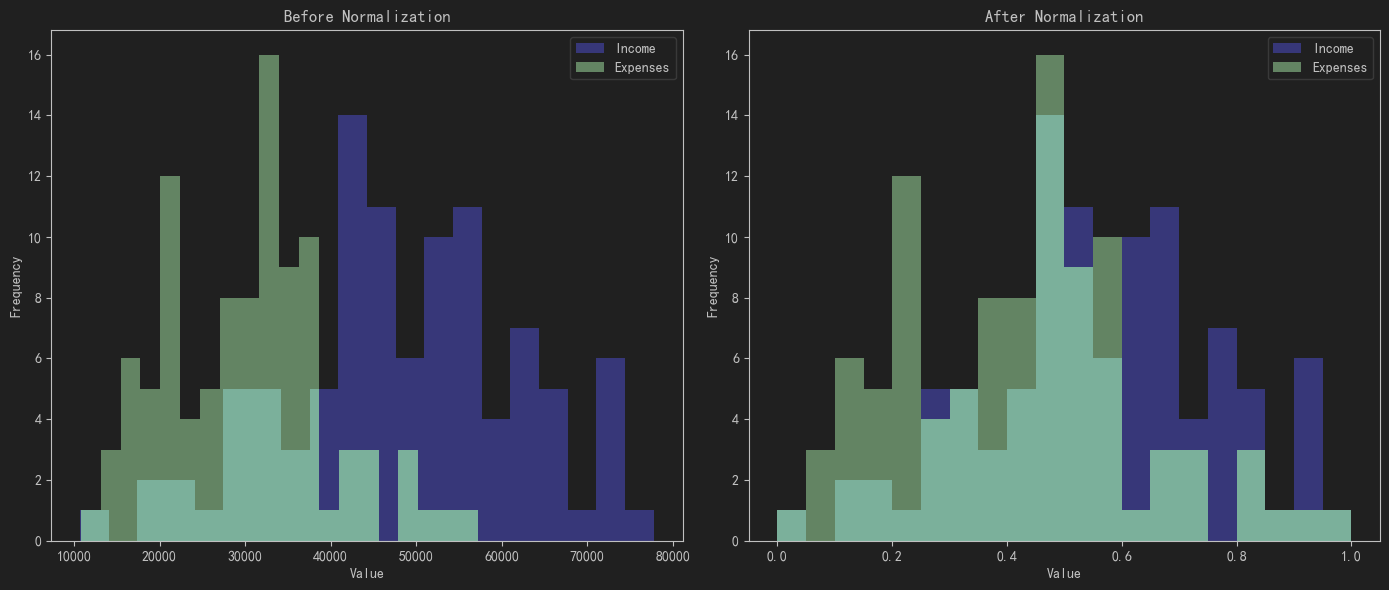
为了避免这种情况，我们需要对数据进行归一化处理。常见的归一化方法有两种：Min-Max归一化和Z-Score归一化。

• 👮 Min-Max归一化的公式是： $x_{\text{Min-Max}}=\frac{x-x_{\text{min}}}{x_{\text{max}}-x_{\text{min}}}$，它的作用是将数据缩放到0到1之间。

• 👮 Z-Score归一化的公式是： $x_{\text{Z-Score}}=\frac{x-\mu }{\sigma }$，其中 $\mu$ 是数据的均值，$\sigma$是标准差。

这种归一化方法不仅考虑了数据的范围，还考虑了数据的分布情况，使得归一化后的数据具有均值为0、方差为1的特性。

归一化在神经网络中的作用是显而易见的。它可以减少特征间的量纲差异，让网络的输入更加均匀，从而提高训练的稳定性和收敛速度。

如果没有归一化，网络可能会陷入梯度消失或梯度爆炸的困境，导致训练过程异常艰难。

二、Batch Normalization的基本原理

那么，Batch Normalization又是如何在归一化的基础上进一步优化神经网络的呢？

这就要从它的提出背景说起。在深度学习中，有一个问题一直困扰着研究人员，那就是内部协变量偏移（Internal Covariate Shift）。

简单来说，随着网络层数的加深或训练的进行，输入数据的分布会发生变化。

这种变化会导致训练过程变得非常缓慢，因为每一层都需要不断地调整自己的参数来适应新的输入分布。

2.1 设计思想

为了解决这个问题，Batch Normalization应运而生。它的核心思想是：既然输入数据的分布会不断变化，那我们就在每一层的输入处进行归一化处理，让数据始终保持在一个相对稳定的分布上。

图2. 数据分布

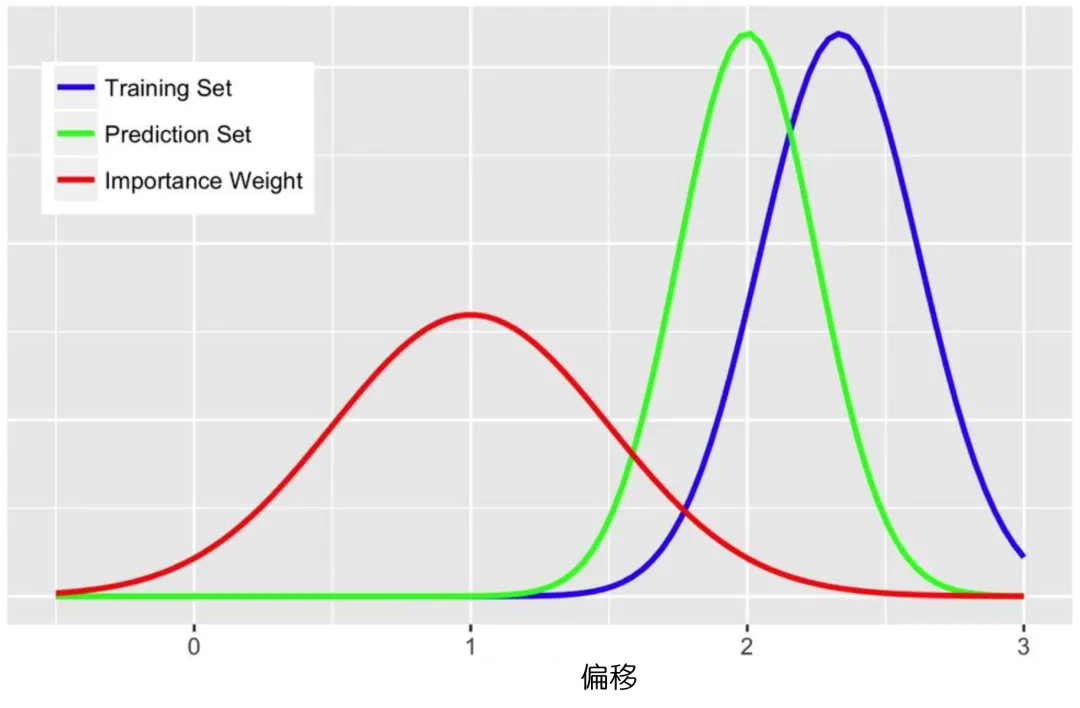
这样一来，每一层的训练过程就会变得更加平稳，收敛速度也会大大加快。

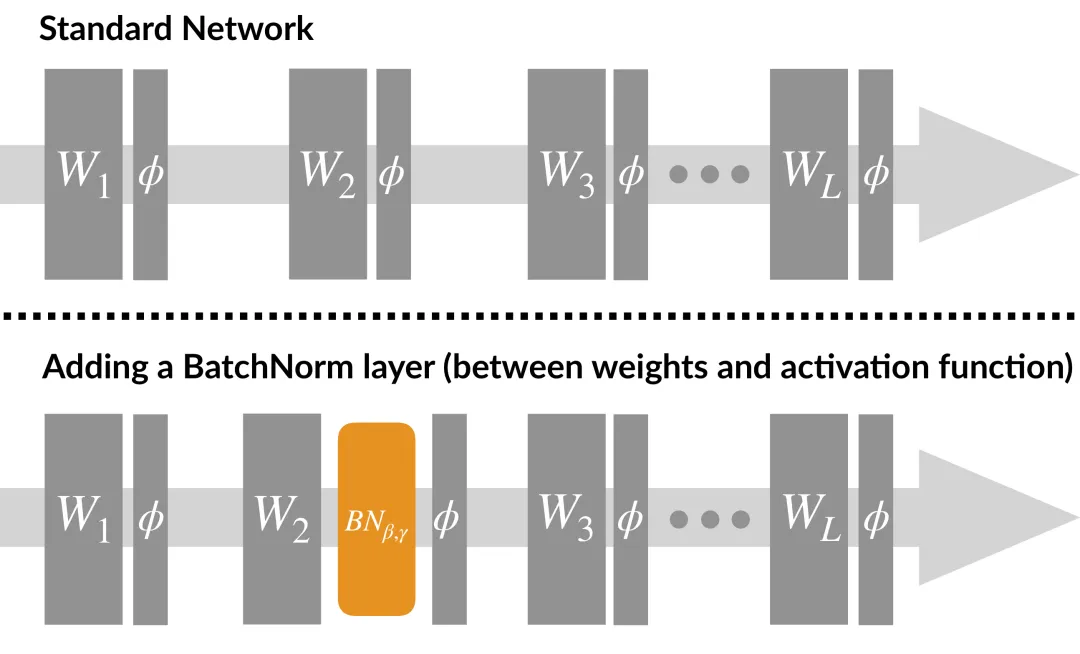
在神经网络中，Batch Normalization通常放在卷积层或全连接层之后、激活函数之前。这是因为归一化后的数据更适合进行非线性变换，而激活函数的作用正是引入非线性。

通过在激活函数之前进行归一化，我们可以让激活函数的输入始终保持在一个相对稳定的分布上，从而提高网络的训练效率。

2.2 基本流程

Batch Normalization的基本流程可以分为四个步骤。

首先，我们需要计算当前批次数据的均值 $\mu$。这个均值是通过将当前批次的所有数据相加，然后除以数据的总数得到的。

接着，我们计算当前批次数据的方差 ${\sigma }^2$。方差的计算公式是：

$${\sigma }^2=\frac{1}{N}\sum _{i=1}^N(x_i-\mu {)}^2$$

其中 $N$是当前批次的数据数量，$x_i$ 是第 $i$ 个数据点。

图3. Batch Normalization基本原理

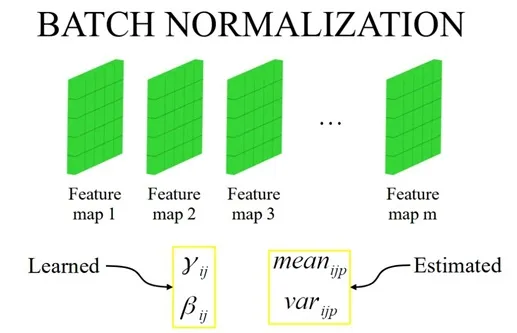
有了均值和方差之后，我们就可以对数据进行归一化处理了。归一化公式是：

$$x^{\prime }=\frac{x-\mu }{\sqrt{{\sigma }^2+ϵ}}$$

其中 $ϵ$ 是一个极小值，用于防止除零。

最后，为了恢复网络的非线性表达能力，我们引入了两个可学习参数 $\gamma$ 和 $\beta$，对归一化后的数据进行缩放和平移。最终的公式是：$y=\gamma x^{\prime }+\beta$。

---

Batch Normalization为什么有效？

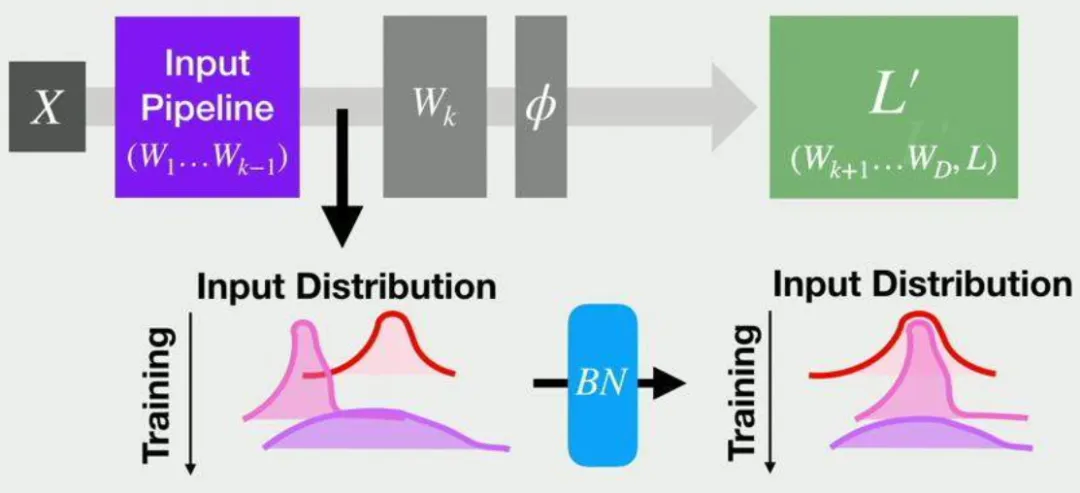
在论文《An empirical analysis of the optimization of deep network loss surfaces》中，作者绘制了VGG和NIN网络在有无BN层的情况下，Loss surface的差异，包含初始点位置以及不同优化算法最终收敛到的local minima位置。

图4. Batch Normalization对模型训练的影响

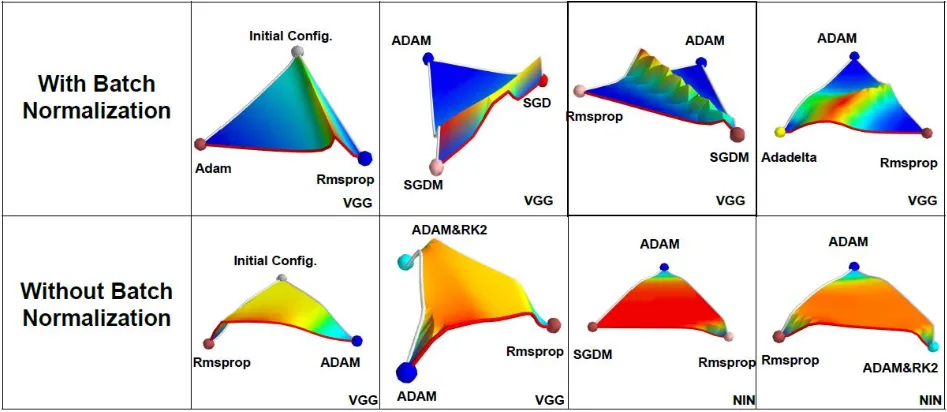
研究发现：没有BN层时，网络的损失曲面存在较大高原，优化困难；加入BN层后，损失曲面变为山峰状，优化更容易。

原因在于，无BN层时，输入分布的均值和方差隐藏在前面层的权重中，调整分布需复杂反向传播。而BN层通过参数γ和β直接调整分布的均值和方差，简化了优化过程，使网络训练更高效。

---

2.3 数学推导

了解了Batch Normalization的基本原理和流程之后，我们再来看看它的数学推导。

首先，我们来推导均值和方差的计算公式。

对于一个维度为$N,C,H,W$的输入张量，均值和方差的计算公式分别为：
$$\mu =\frac{1}{N\times H\times W}\sum _{n=0}^{N-1}\sum _{h=0}^{H-1}\sum _{w=0}^{W-1}X[n,c,h,w]$$
$${\sigma }^2=\frac{1}{N\times H\times W}\sum _{n=0}^{N-1}\sum _{h=0}^{H-1}\sum _{w=0}^{W-1}(X[n,c,h,w]-\mu {)}^2$$
这两个公式的作用是计算当前批次数据的均值和方差，为后续的归一化处理提供依据。

接下来，我们来看归一化公式的推导。

归一化公式是 $x^{\prime }=\frac{x-\mu }{\sqrt{{\sigma }^2+ϵ}}$，它的目的是将数据转换为均值为0、方差为1的分布。

---

为什么要加一个极小值 $ϵ$ 呢？

这是因为当方差 ${\sigma }^2$ 非常接近0时，分母可能会变成0，导致除零错误。

为了避免这种情况，我们在分母中加入一个极小值 $ϵ$，使得分母始终大于0。

---

图5. Batch Normalization数学原理

最后，我们来推导可学习参数 $\gamma$ 和 $\beta$ 的作用。

在归一化之后，数据的分布虽然更加稳定，但同时也失去了原来的尺度和偏移。

为了恢复网络的非线性表达能力，我们需要引入两个可学习参数 $\gamma$和 $\beta$，对归一化后的数据进行缩放和平移。

Batch Normalization公式是：
$$y=\gamma \frac{x-\mu }{\sqrt{{\sigma }^2+ϵ}}+\beta$$
其中，$\gamma$ 的作用是对数据进行缩放，$\beta$ 的作用是对数据进行平移。

通过这两个参数，我们可以将归一化后的数据调整到更适合网络学习的分布上。

三、Batch Normalization对模型训练的影响

Batch Normalization对模型训练的影响是多方面的。

首先，它可以加速训练收敛。

Batch Normalization通过将激活输入值分布在非线性函数的梯度敏感区域，可以避免梯度消失问题，从而加快训练速度。

其次，它可以提升模型的泛化能力。

Batch Normalization通过归一化操作减少模型对特定数据分布的依赖，使得模型在面对新的数据时能够更好地适应，从而增强模型的泛化能力。

图6. Batch Normalization在模型中的位置

除了这些优点之外，Batch Normalization还可以简化调参过程。

由于它对学习率和参数初始化的宽容性，我们在训练过程中不需要花费太多时间去调整这些参数，大大减少了调参的复杂度，提高了训练的效率。

---

然而，Batch Normalization也并非万能的。它也有一些局限性。

例如，它对小批量数据比较敏感。当批量大小较小时，计算得到的均值和方差可能会不够准确，从而影响Batch Normalization的效果。

此外，在某些情况下，Batch Normalization可能会导致训练过程不稳定。

因此，在实际应用中，我们需要根据具体的情况来选择是否使用Batch Normalization，以及如何调整它的参数。

---

- 结语 -

通过以上内容的介绍，我们对Batch Normalization的数学原理及其在神经网络中的作用有了一个全面的了解。

Batch Normalization通过归一化操作解决了内部协变量偏移的问题，加速了训练收敛，提升了模型的泛化能力，并简化了调参过程。

目前，Batch Normalization已经成为深度学习中一种不可或缺的技术，被广泛应用于各种神经网络模型中。

注：本文中未声明的图片均来源于互联网