一、随机事件与样本空间

1. 原理讲解

2. 类型与关系

3. 案例计算

4. 应用场景

二、古典概率与条件概率

1. 古典概率 (Classical Probability)

2. 条件概率 (Conditional Probability)

三、全概率公式与贝叶斯公式

1. 全概率公式 (Law of Total Probability)

2. 贝叶斯公式 (Bayes‘ Theorem)

3. 两者的逻辑关联

一、随机事件与样本空间

1. 原理讲解

概率论研究的是不确定性（随机性）的规律。它的基础是两个核心概念：

样本空间 (Sample Space)：记作 $S$ 或 $\Omega$ 。它是一个随机试验所有可能结果的集合。每个结果称为一个样本点。
随机事件 (Random Event)：是样本空间的子集。它表示我们“关心”的某些结果的集合。

2. 类型与关系

必然事件：一定会发生的事件，即样本空间 $S$ 本身。（例如：掷骰子点数小于7）
不可能事件：一定不会发生的事件，即空集 $\varnothing$ 。（例如：掷骰子点数为0）
基本事件：只包含一个样本点的事件。
复合事件：包含多个样本点的事件。

关系：事件是样本空间的子集，所以集合的运算（交 $\cap$ 、并 $\cup$ 、补 $\bar{A}$ ）完全适用于事件。

$A \cap B$ ：事件A 和事件B 同时发生。
$A \cup B$ ：事件A 或事件B 至少有一个发生。
$\bar{A}$ ：事件A 不发生（对立事件）。

3. 案例计算

试验：掷一颗六面公平骰子。
- 样本空间 $S$ ：{1, 2, 3, 4, 5, 6}
- 事件A（点数为偶数）：{2, 4, 6}
- 事件B（点数大于4）：{5, 6}
- 事件A与B的交集 $A \cap B$ ：{6} （即点数大于4且是偶数）
- 事件A与B的并集 $A \cup B$ ：{2, 4, 5, 6} （即点数为偶数或大于4）

4. 应用场景

构建任何概率问题的第一步都是明确样本空间。它是我们计算概率的“分母”，是所有可能性的全集。无论是游戏抽卡、产品质量检测还是社会调查，都需要先定义清楚所有可能的结果。

1. 游戏抽卡

一句话定义： 卡池里所有可被抽到的特定卡牌的集合。

简单说明：假设一个卡池里有100张卡，包括80张普通卡（N）、15张稀有卡（R）和5张超级稀有卡（SSR）。那么样本空间就是这100张各不相同卡的集合 {卡1, 卡2, 卡3, ..., 卡100}。你每次抽卡，结果必然是这个集合中的某一个元素。

2. 产品质量检测

一句话定义： 被抽查的产品所有可能的质量状态结果的集合。

简单说明：最简单的情况是产品只有“合格”与“不合格”两种状态。那么样本空间就是 {合格, 不合格}。如果要更精细，样本空间可以是所有可能缺陷类型的集合，例如 {合格, 外观瑕疵, 功能故障, 包装损坏, ...}。

3. 社会调查

一句话定义： 所有被调查者对于某个问题可能给出的所有答案的集合。

简单说明：例如，调查“您对当前政策的满意度如何？”，选项为“非常满意”、“满意”、“一般”、“不满意”、“非常不满意”。那么样本空间就是这个选项集合 {非常满意, 满意, 一般, 不满意, 非常不满意}。每个被访者的回答就是这个空间里的一个结果。

核心总结

场景样本空间 (S) “一次试验” “一个结果”
游戏抽卡 所有卡牌的集合抽一次卡抽到某一张特定的卡
质量检测 所有质量状态的集合检测一个产品该产品被判定为某种状态
社会调查 所有可能答案的集合询问一个人这个人给出的某个特定答案

关键在于： 样本空间必须穷尽所有可能（不能遗漏），且结果之间互斥（一个结果发生，其他结果就不发生）。

场景	样本空间 (S)	“一次试验”	“一个结果”
游戏抽卡	所有卡牌的集合	抽一次卡	抽到某一张特定的卡
质量检测	所有质量状态的集合	检测一个产品	该产品被判定为某种状态
社会调查	所有可能答案的集合	询问一个人	这个人给出的某个特定答案

二、古典概率与条件概率

1. 古典概率 (Classical Probability)

原理：适用于样本空间有限且每个基本事件发生的可能性完全相同的场景。概率计算转化为“数数”问题。
公式：事件 $A$ 发生的概率
案例：
- 抽扑克牌，抽到A的概率： $P = \frac{4}{52} = \frac{1}{13}$
- 掷骰子得到偶数的概率： $P = \frac{3}{6} = \frac{1}{2}$
应用：赌博游戏（骰子、轮盘）、抽奖、简单的随机抽样。前提是“公平”，即等可能性。

2. 条件概率 (Conditional Probability)

原理：在已知某个事件B已经发生的条件下，另一个事件A发生的概率。它引入了“信息”的概念，信息会改变概率。
公式： $P(A|B) = \frac{P(A \cap B)}{P(B)}$ （要求 $P(B) > 0$ ）
- $P(A|B)$ 读作“在B发生的条件下A发生的概率”。
- 分子 $P(A \cap B)$ 是A和B同时发生的概率。
- 分母 $P(B)$ 是已知条件发生的概率。
案例：
- 掷一颗骰子。已知掷出的点数是奇数（事件B={1,3,5}），求该点数大于3（事件A={4,5,6}）的概率。
- $A \cap B = {5}$
- $P(A|B) = \frac{P(A \cap B)}{P(B)} = \frac{1/6}{3/6} = \frac{1}{3}$
应用：几乎所有现实场景！天气预报（已知今天是晴天，明天下雨的概率）、推荐系统（已知用户购买了A商品，其购买B商品的概率）、医疗诊断（已知检测结果为阳性，真实患病的概率）。

三、全概率公式与贝叶斯公式

这两个公式是条件概率的延伸，共同解决了“由因推果”和“由果溯因”的问题。

1. 全概率公式 (Law of Total Probability)

原理：如果事件 $B$ 的发生总是与一系列互斥（不相交）且完整（覆盖所有可能性）的原因 $A_1, A_2, ..., A_n$ 之一有关，那么事件 $B$ 的总概率可以通过将所有不同途径导致 $B$ 发生的概率加总得到。
公式：
$P(B) = P(B|A_1)P(A_1) + P(B|A_2)P(A_2) + ... + P(B|A_n)P(A_n)$
案例（工厂质检）：
- 某工厂有三条生产线（ $A_1$ , $A_2$ , $A_3$ ），产量占比分别为50%，30%，20%（即 $P(A_1)=0.5$ , $P(A_2)=0.3$ , $P(A_3)=0.2$ ）。
- 各生产线的次品率分别为1%，2%，3%（即 $P(B|A_1)=0.01$ , $P(B|A_2)=0.02$ , $P(B|A_3)=0.03$ ）。
- 问：随机抽一个产品，它是次品( $B$ )的概率是多少？
- 计算：
  $P(B) = 0.01 \times 0.5 + 0.02 \times 0.3 + 0.03 \times 0.2 = 0.005 + 0.006 + 0.006 = 0.017$
应用：用于计算一个复杂事件的总概率，当该事件可以通过多种不同的、互斥的路径发生时。

2. 贝叶斯公式 (Bayes‘ Theorem)

原理：它解决的问题是“逆概率”。当我们观察到结果 $B$ 发生了，要反过来推断这个结果是由某个原因 $A_i$ 造成的概率是多少。它用新证据（ $B$ ）来更新我们对该原因（ $A_i$ ）的信念（从先验概率 $P(A_i)$ 更新为后验概率 $P(A_i|B)$ ）。

公式：
$P(A_i|B) = \frac{P(B|A_i)P(A_i)}{P(B)} = \frac{P(B|A_i)P(A_i)}{\sum_{j=1}^{n} P(B|A_j)P(A_j)}$

分母 $P(B)$ 就是由全概率公式计算得出的。

案例（疾病检测）：

某疾病患病率（先验概率）
- P(患病)=0.01（即人群中1%的人患有该疾病）
- P(健康)=1−P(患病)=0.99（即人群中99%的人是健康的）
检测准确率：P(阳性|患病) = 0.99 (灵敏度)，P(阳性|健康) = 0.05 (假阳性率)
问：如果一个人检测结果是阳性，他真正患病的概率 P(患病|阳性)是多少？
计算：
1. 用全概率公式计算 P(阳性):P(阳性)=P(阳性∣患病)⋅P(患病)+P(阳性∣健康)⋅P(健康)，P(阳性)=0.99×0.01+0.05×0.99=0.0099+0.0495=0.0594
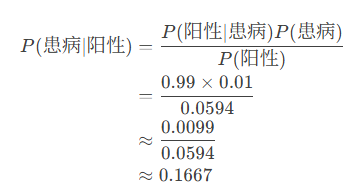
2. 用贝叶斯公式计算后验概率:
结论：尽管检测“很准确”，但一次阳性结果下真正患病的概率只有16.67%。这是因为患病率低，假阳性人数远多于真阳性人数。这体现了贝叶斯“更新信念”的核心思想。
应用：
- 机器学习：垃圾邮件过滤（已知邮件内容，判断是垃圾邮件的概率）。
- 医疗诊断：基于症状和检测结果诊断疾病。
- 金融风控：评估用户交易欺诈的概率。
- 人工智能：贝叶斯网络是重要推理工具。

3. 两者的逻辑关联

全概率公式是正向思维：“原因” → “结果”。（由因推果）
贝叶斯公式是逆向思维：“结果” → “原因”。（由果溯因）
关键联系：贝叶斯公式的分母 $\mathbf{P(B)}$ 必须通过全概率公式来计算。没有全概率公式提供的“总概率”，贝叶斯公式就无法完成准确的逆向推理。