哈希（散列）方法是对插入的数据通过哈希函数计算出一个哈希地值，并将这个哈希地址作为储存改数据的地址，这样下次再查找这个数据时，只需要通过哈希函数再获取到该地址然后直接去拿就好
这样就做到了不经过任何比较，一次就能从表中拿到元素的O(1)的时间复杂度，他将哈希函数计算出来的值和目标值建立了一一映射的关系
比如有一个数组大小为5 下标为0 1 2 3 4
再插入值时，我对他进行 %5 取余操作，再储存2时就映射到了下标2，于是将值放到数组下标2的位置，%5 这就是一个简单的哈希函数而构建出来的表（这个数组）就称为哈希表（散列表）
冲突
对于刚刚的例子，很容易看出单数据多了，就会出现不同的数据映射到相同的位置，这种不同的数据通过哈希函数计算出来了相同的哈希地址，就称为哈希冲突或者哈希碰撞，把具有相同哈希值但是不是相同的数据称为同义词
冲突的避免
要知道哈希冲突时不可解决的，但数据量大之后，什么可能都会出现，而我们能做的是减低冲突率
避免哈希函数的最有效的办法是优化哈希函数，哈希函数计算出来的地址应该要平均分布到空间中，如果有m个地址，那么哈希函数计算出来的值就应该平均的分布到0 - m-1
负载因子的调节
负载因子的定义 α = 数据的总数 / 哈希表的长度
α是哈希函数装满程度的标注因子，且发送哈希冲突的可能性和α成正比，因为数据越多，发送哈希冲突的可能性更大
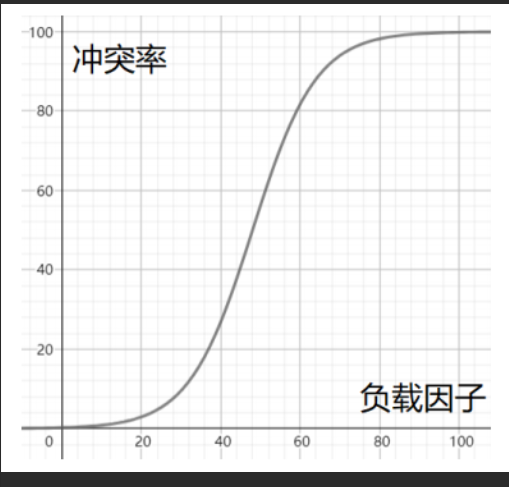
所以要降低冲突率就要减低负载因子，而储存数据的总数是不能变的，于是需要扩大哈希表的大小
冲突的解决分为开散列和闭散列
闭散列
当冲突发生时，哈希表还没有被填满，所以表中一定还有空的位置，那么就找出这个空的位置来放冲突元素
线性探测
若计算出的哈希地址冲突了，就往后继续探测一个空的位置，直接放入
再删除元素的时候，采用的是标志位的伪删除法，因为使用线性探测法，一个哈希地址对应的有可能是多个元素，而这其他的元素，要基于这个哈希地址来往后查找，如果这个位置被删除了，那么就表示这里就没有元素，而和他冲突的元素也就不存在了
二次探测
线性探测的缺点是冲突元素容易产生堆积，这于寻找下一个位置有关系，因为是挨个挨个找到空位置，而二次探测为了避免该问题是跳着寻找空位置的，寻找下标的公式是
，也可以是h0-i^2，Hi是最终的下标，H0是计算出来的冲突地址，m是表大小，i是1 2 3.... 是动态递增的，冲突一次i就加一
有研究表明，但α 小于0.5时，新的数据一定能插入，且任何位置都不会被探测俩次，因此再还有一般的空位置时，就不会存在冲突的情况，那么再搜索时就不用考虑冲突的情况，但如果大于了0.5就要考虑扩容表了
所以哈希表对空间的利用率比较底，这是哈希的缺陷
开散列 哈希桶
开散列又叫链地址法，将冲突的元素归于一个集合，每一个子集称为一个桶桶中的元素又链表联系起来
实现：在哈希表中储存的是一个链表，当冲突的元素就直接储存再这个链表中，再查找时就先通过哈希函数找到这个链表，再遍历这个链表来获取到元素，因为冲突的次数一般都是常熟级的，所以遍历这个链表的时间也可以近似忽略，所以搜索还是O(1) 的复杂度
但当元素过多之后，遍历这个链表所需要的时间也不能被接受了，于是这个桶也可以是另一个哈希表或者是一颗搜索树
虽然哈希的发展是一直在和哈希冲突做斗争，但是我们在平时使用时，哈希冲突发送的情况也不是很频繁，对于增删查改的时间复杂度视为是O(1) 的
)
