一，图的遍历逻辑

1.之前我们学了图的存储，可以邻接表存和邻接矩阵存。现在我们要学习图的遍历操作和树类似可以分为深度遍历和广度遍历，而深度遍历也是用递归实现，广度遍历是用队列实现

2.深度遍历(DFS)

a.确定起点

b.找到一条边按顺时针方向（准确来说存储结构方向）来对这个节点进行处理

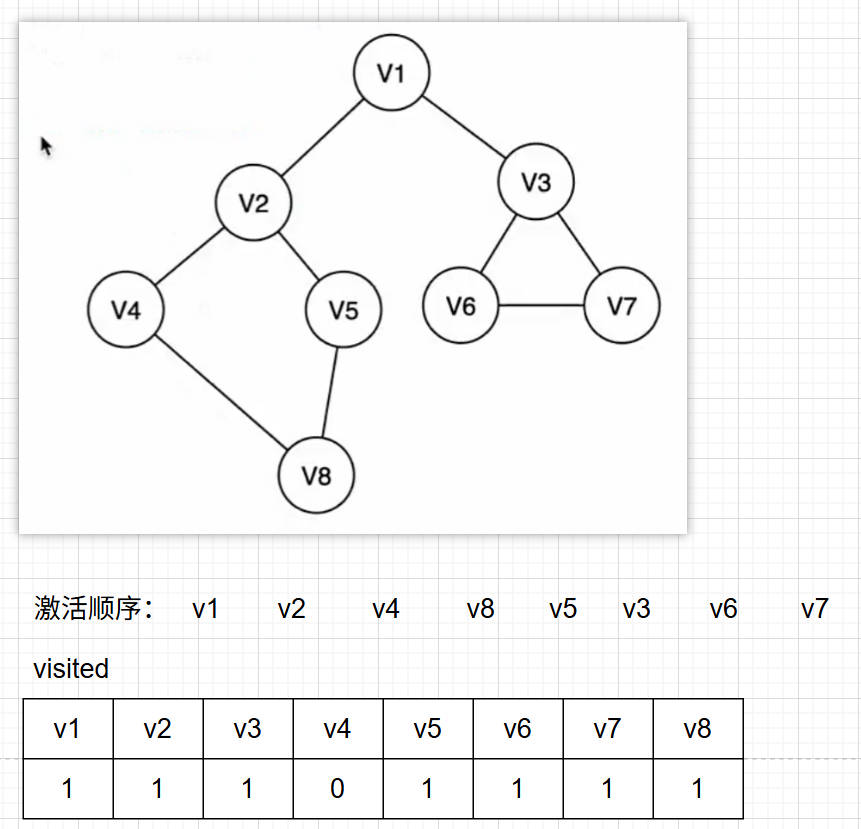如左图当我们选择v1为起点找到和v2的这条边，此时激活了v2那么就需要处理v2的三条边，但v1我们已经走过了。由于图没有树那样严格按照1：n的关系因此会有重复访问的节点。因此我们可以引入一个已访问节点的表

3.广度遍历（层次遍历） (BFS)

广度遍历首先也是需要一个队列，当我们访问完一个节点就把激活的新节点入队，然后每出队一个节点就访问它并把新激活的节点入队。但是和树不一样，图也是有可能重复访问的，比如从v1开始访问到v3，当我们访问完v3会激活v1、v6、v7，但是v1已经被访问过了，因此需要引入一个存储已访问节点的表

二，代码实现

1.深度遍历

static int MGraphVisited[MaxNodeNum]={0};
void DFSMGraph(MGraph *graph, int v) {//访问节点visitMGraphNode(&graph->vex[v]);//将节点标记为已访问MGraphVisited[v]=1;//激活连通的节点，排除已访问的for (int i=0;i<MaxNodeNum;i++) {if (isEdge(graph->edges[v][i])&&MGraphVisited[i]==0) {//满足条件递归DFSMGraph(graph,i);}}
}