整体概述

难度：1000 $→\rightarrow$ 1500 $→\rightarrow$ 2000

1567B. MEXor Mixup

标签：前缀和
前置知识：无
难度：Div.2.B 1000

题目描述：

输入格式：

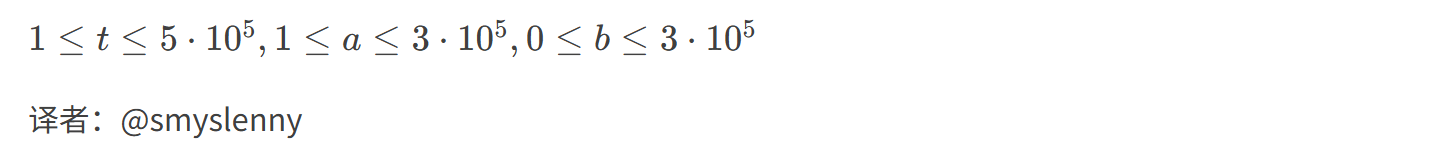
输出格式：

样例输入：

样例输出：

解题思路：

首先我们知道，想要让 $MEX = a$ 则 $[0, a - 1]$ 范围内的数都得选，发现 $1≤a≤3⋅1051\le a\le 3·10^5$ 那么我们可以预处理出所有 $[0, x]$ 的异或和。
接着要让 $x or = b$ ，我们设 $xor_{i=0}^a-1=c$ ，那么还差 $b^c$ 就可以凑出该数字。
需要注意的是如果 $c = a$ ，那么我们需要拿两个数字凑出 $c$ ，否则只需要直接再增加一个 $c$ 即可。

如果 $c = 0$ 表示直接凑出 $b$ 了，那么不需要再加数字了。
预处理出前缀异或和，查询复杂度 $O (1)$ ，总复杂度 $O(3·10^5)$ 。

完整代码

#include<bits/stdc++.h>
#define Size(x) ((int)(x).size())
#define int long long
using namespace std;
const int N = 3e5+5;
int pre[N];
inline void solve(){int a,b; cin >> a >> b;int c = pre[a-1]^b;if(!c) cout << a << '\n';else if(c == a) cout << a+2 << '\n';else cout << a+1 << '\n';
}
signed main(){ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);int T; cin >> T;for(int i=1;i<N;i++) pre[i] = pre[i-1]^i; while(T--) solve();return 0;
}

501C. Misha and Forest

标签：拓扑排序
前置知识：无
难度：Div.2.C 1500

题目描述：

输入格式：

输出格式：

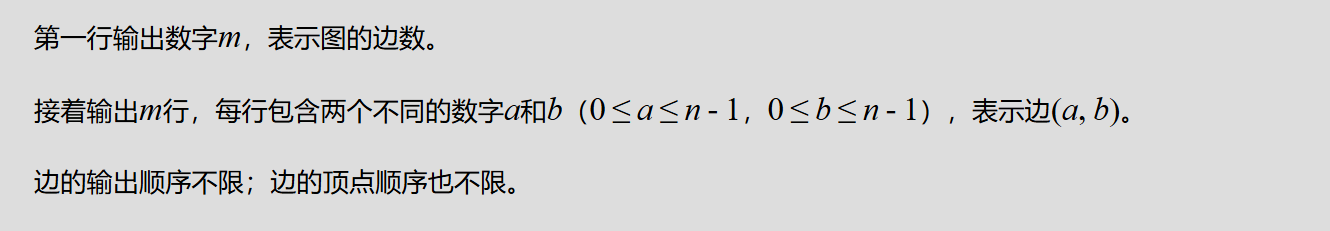
样例输入：

2
1 1
1 0

样例输出：

2
1 0
2 0

1
0 1

解题思路：

由于是一片森林，不存在环，那么一定有某些节点的度为 $1$ ，而我们又知道这些节点的相邻节点编号的异或和，就是相邻节点的编号，那么这些边就都可以确定了。
接着在未确定的边中删去这些边，就会又有某些节点度为 $1$ ，这个过程其实就是拓扑排序的过程，我们跑一遍拓扑排序，每次连边即可。

需要注意的是，如果出队列的点度为 $0$ 表明已经连过了，此时跳过即可。
总复杂度 $O (n)$ 。

完整代码

#include<bits/stdc++.h>
#define Size(x) ((int)(x).size())
#define int long long
using namespace std;
const int N = (1<<16)+5;
int n,d[N],eor[N];
vector<pair<int,int>> res;
inline void solve(){cin >> n;for(int i=0;i<n;i++) cin >> d[i] >> eor[i];queue<int> qu;for(int i=0;i<n;i++) if(d[i] == 1) qu.push(i);while(!qu.empty()){int u = qu.front(); qu.pop();int v = eor[u];if(!d[u]) continue;res.push_back({u,v});eor[v] ^= u;if(--d[v] == 1) qu.push(v);}cout << res.size() << '\n';for(auto [u,v]:res) cout << u << ' ' << v << '\n';
}
signed main(){ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);int T; T = 1;while(T--) solve();return 0;
}

755D. PolandBall and Polygon

标签：树状数组
前置知识：无
难度：8VC Venture Cup 2017.D 2000

题目描述：

输入格式：

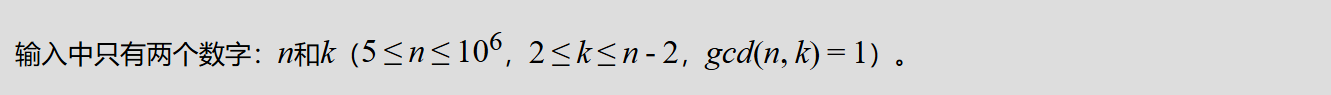
输出格式：

样例输入：

5 2

10 3

样例输出：

2 3 5 8 11

2 3 4 6 9 12 16 21 26 31

解题思路：

通过画图我们发现， $画一条线增加的区域数$ 等同于 $与原有线段的交点个数 + 1$ ，所以问题就转化为每次给出线段的两个端点，求有多少个交点。
我们发现所有相交线段的两个端点分别位于线段两侧，即有且仅有一个端点在新线段的 $(l, r)$ 间。由于每条线段两个端点间的距离是固定的，因此我们仅需统计在 $(l, r)$ 内的节点的总度数，即为交点个数。

需要注意的是，我们用的 $[l, r]$ 区间需要是劣弧的那一段。
那么我们用树状数组进行单点修改，区间查询，总复杂度 $O(n·log_{2}n)$ 。

完整代码

#include<bits/stdc++.h>
using namespace std;
const int N = 1e6+5;
int n,k,tr[N];
inline void add(int x,int v){for(int i=x;i<=n;i+=i&-i) tr[i] += v;
}
inline long long sum(int l,int r){if(l > r) return 0;long long ans = 0;for(int i=r;i;i&=i-1) ans += tr[i];for(int i=l-1;i;i&=i-1) ans -= tr[i];return ans;
}
inline void solve(){cin >> n >> k;long long ans = 1;for(int i=1,p=1,l,r,cur;i<=n;i++){l = p,r = p = l+k > n ? l+k-n : l+k;if(l > r) swap(l,r);cur = (r-l-1) <= (n-r+l-1) ? sum(l+1,r-1) : sum(r+1,n) + sum(1,l-1); ans += cur+1;cout << ans << ' ';add(l,1), add(r,1);}
}
signed main(){ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);int T; T = 1;while(T--) solve();return 0;
}