题意:给出一棵树,按照以下方式操作
对于当前的所有任意子树,选出任何一个点从中删除,然后作为新子树的根插入到新的树中,以此递归往复,直到原来的树中节点全部进入新树,问新树最多有多少个叶子节点。
然后如果根节点只有一个联通的点,那么自己也算叶子
思路:Codeforces Global Round 26 (A - E) - Lu_xZ - 博客园
1.首先对于题意进行解析,这个操作是在干什么,然后发现,任意相邻的节点不能同时为叶子节点,然后如果我们把叶子节点归为一类,就会发现所有的叶子节点就是最大独立集
最大独立集:选出的点集中,任何一个子集都不满足在原图上可以互相抵达
举例:1-2-3-4-5-6,1作为根节点可以跟3连,2就变成了子节点,4-5-6作为新的子树
也就是说为什么发现的,任何一个点想成为叶子节点,只要在当前子树中选择一个相邻节点,自己就可以变成叶子节点
2.发现是最大独立集,那么接下来该如何是好?因为任何一个点都可能成为根节点,于是乎考虑换根dp,这个应该要稍微靠一点感觉……
任何一个节点的子树所选中的状态不会因为另外一边子树的状态受影响,这是换根dp的关键,因为这样才能顺序的求出
3.于是乎开始dp,首先求出假设某一个节点是根节点的子树选择情况,这里就默认选1了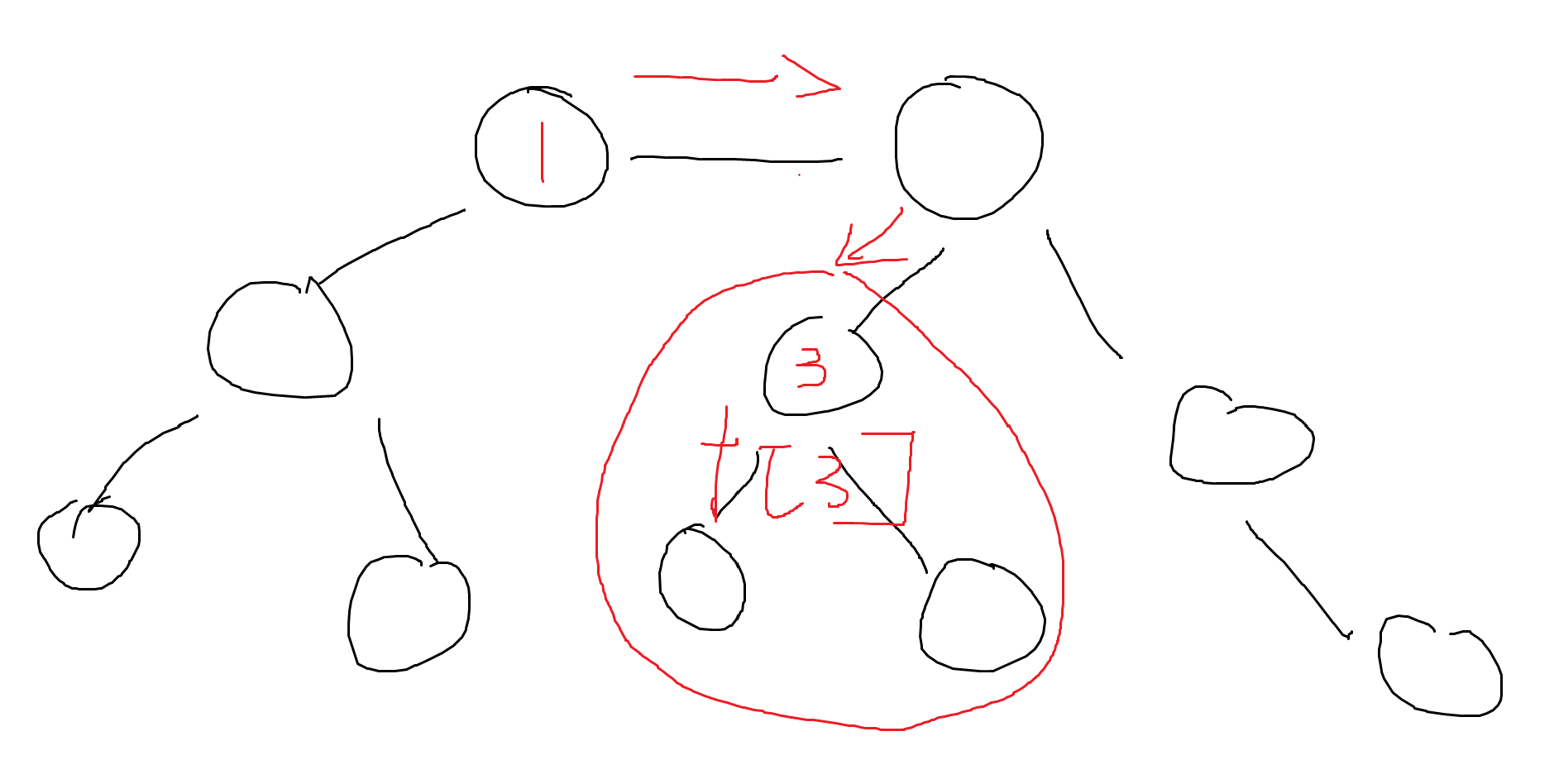
f[3]代表3节点的情况,但是要分类f[3][0/1],代表图中形状的子树3节点作为叶子节点和不是叶子节点的情况
之后得到状态转移方程
f[x][0]+=max(f[u][0],f[u][1]) 当前节点不是叶子节点,那么相邻节点可以是叶子节点也可以不是
f[x][1]+=f[u][0] 当前节点是叶子节点,相邻节点只能不是叶子节点
接下来换根
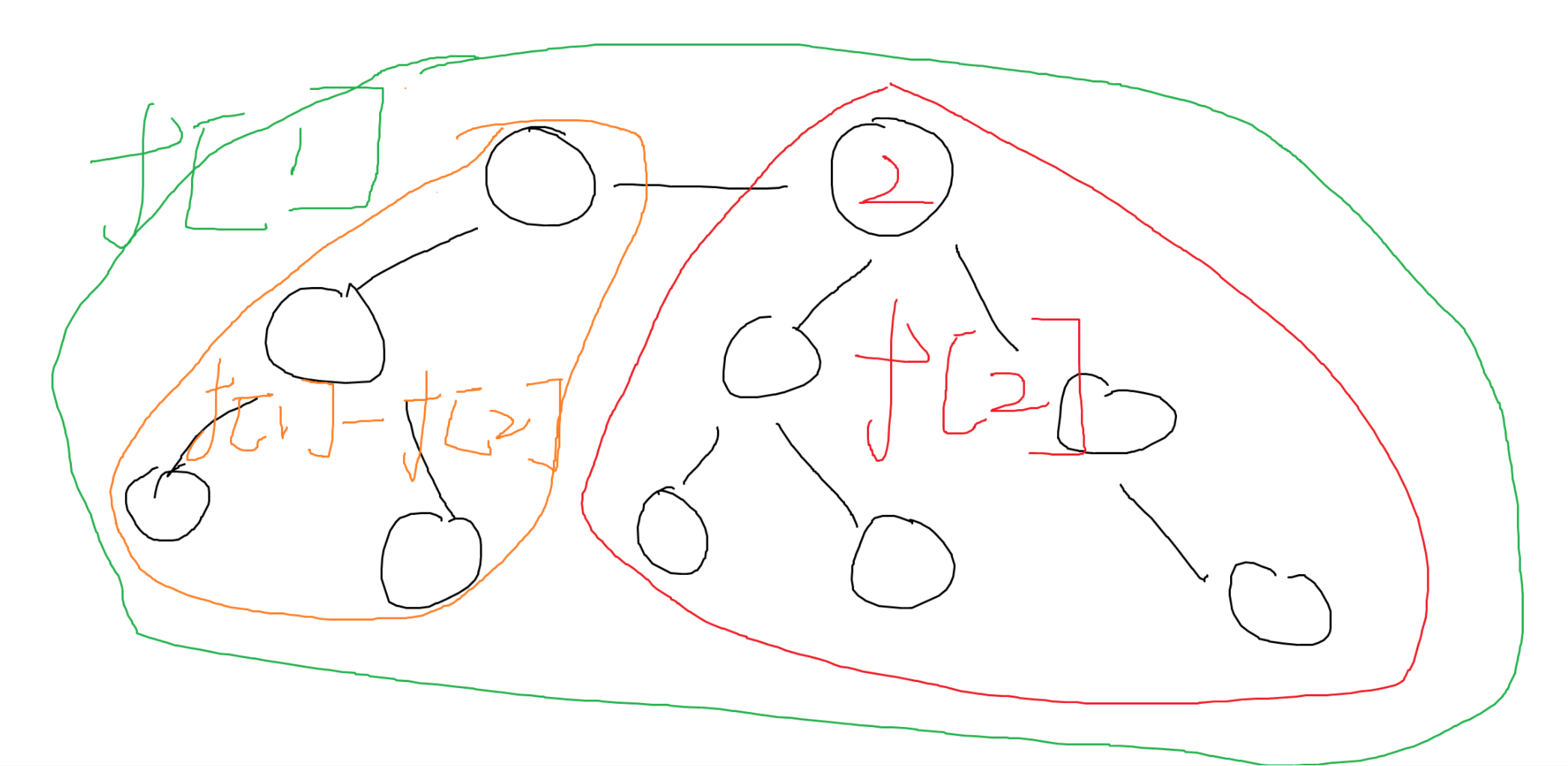
假设以2为根,f[2]所拥有的状态只是红色部分子树,而另一边就可以由父节点减去当前子树得到
然后在此基础上进行拼接,就完成了换根的操作
然后因为另一边子树只受到子树根节点的影响,所以才能进行换根dp
我们将橙色区域称为temp(f[1]-f[2])
那么新的dp转移
g[x][0]=std::max(g[fa][1],f[x][0]+temp); g[fa][1]其实跟f[2][0]+(f[1]-f[2])[1]是一致的,然后另一种拼接求最多的那个
g[x][1]=temp+f[x][1];
完成dp的状态转移
最后求答案g[x][0]+(ve[x].size()==1);
ve[x].size()==1是因为根节点本身可能也是叶子节点,但在dp的过程中,自己作为叶子节点是不可以的,是别人作为非叶子节点的,自己才可以选择作为叶子节点,根作为第一个节点没有能力选择一个父节点作为非叶子节点,只能是自己,先有非叶子节点,才有叶子节点
任何一个点想成为叶子节点,只要在当前子树中选择一个相邻节点,自己就可以变成叶子节点
扫描完成全部,那么本道题就结束了
代码
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define IOS \std::ios::sync_with_stdio(0); \std::cin.tie(0); \std::cout.tie(0)const int N = 3e5 + 5;
const int INF = 1e18;
const int MOD = 998244353;
// const int MOD=1e9+7;
// const int MOD=100003;
const int maxn=5e5+10;std::vector<int> ve[N];
int f[N][2];
int g[N][2];void dfs(int x,int fa){f[x][0]=0;f[x][1]=1;for(auto i : ve[x]){if(i==fa) continue;dfs(i,x);f[x][1]+=f[i][0];f[x][0]+=std::max(f[i][0],f[i][1]);}
}int ans=0;
void dfs2(int x,int fa){int temp=g[fa][0]-std::max(f[x][0],f[x][1]);g[x][1]=temp+f[x][1];g[x][0]=std::max(g[fa][1],f[x][0]+temp);temp=g[x][0]+(ve[x].size()==1);ans=std::max(ans,temp);for(auto i : ve[x]){if(i==fa) continue;dfs2(i,x);}
}void solve(){int n;std::cin >> n;ans=0;for(int i=1;i<=n;i++){ve[i].clear();f[i][0]=f[i][1]=g[i][0]=g[i][1]=0;}for(int i=1;i<n;i++){int x,y;std::cin >> x >> y;ve[x].push_back(y);ve[y].push_back(x);} dfs(1,0);g[1][0]=f[1][0];g[1][1]=f[1][1];ans=g[1][0]+(ve[1].size()==1);for(auto i : ve[1])dfs2(i,1);std::cout << ans << '\n';
}signed main()
{IOS;int t = 1;std::cin >> t;while (t--){solve();}
}



)







)

深入解析)

)


管理机制)