评价决策类-Topsis法学习笔记

问题的提出

生活中我们常常要进行评价，上一篇中的层次分析法，通过确定各指标的权重，来进行打分，但层次分析法决策层不能太多，而且构造判断矩阵相对主观。那有没有别的方法呢？

例题引入

明星Kun想找个对象，但喜欢他的人太多，不知道怎么选，经过层层考察，留下三个候选人。

候选人	颜值	脾气（争吵次数）
A	9	10
B	8	7
C	6	3

理想情况下：
- 最好的对象应该是颜值9，脾气3
- 最差的对象应该是颜值6，脾气10
那怎么衡量A、B、C和最好、最差的距离呢？
- 把（9，3），（6，10）最为二维平面的一个点（如图中的红点和蓝点）
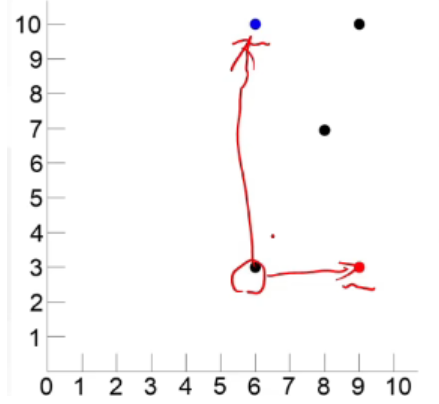
距离最好点最近或者距离最差点最远的点就是综合条件最好的（如上图中的红笔所圈的点）

基本概念

C. L. Hwang 和 K. Yoon 于 1981 年首次提出 TOPSIS (Technique for Order Preference by Similarity to an Ideal Solution)，可翻译为逼近理想解排序法，国内常简称为优劣解距离法。

TOPSIS 法是一种常用的综合评价方法，能充分利用原始数据的信息，其结果能精确地反映各评价方案之间的差距。

TOPSIS 法引入了两个基本概念：

理想解：设想的最优的解 (方案)，它的各个属性值都达到各备选方案中的最好的值；
负理想解：设想的最劣的解 (方案)，它的各个属性值都达到各备选方案中的最坏的值。

方案排序的规则是把各备选方案与理想解和负理想解做比较，若其中有一个方案最接近理想解，而同时又远离负理想解，则该方案是备选方案中最好的方案。TOPSIS 通过最接近理想解且最远离负理想解来确定最优选择。

模型原理

TOPSIS 法是一种理想目标相似性的顺序选优技术，在多目标决策分析中是一种非常有效的方法。它通过归一化后 (去量纲化) 的数据规范化矩阵，找出多个目标中最优目标和最劣目标 (分别用理归想一解化和反理想解表示), 分别计算各评价目标与理想解和反理想解的距离，获得各目标与理想解的贴近度，按理想解贴近度的大小排序，以此作为评价目标优劣的依据。贴近度取值在 0~1 之间，该值愈接近 1, 表示相应的评价目标越接近最优水平；反之，该值愈接近 0, 表示评价目标越接近最劣水平。

基本步骤

将原始矩阵正向化
将原始矩阵正向化，就是要将所有的指标类型统一转化为极大型指标。
正向矩阵标准化
标准化的方法有很多种，其主要目的就是去除量纲的影响，保证不同评价指标在同一数量级，且数据大小排序不变。
计算得分并归一化
$Si=Di−Di++Di−S_i = \frac{D_i^-}{D_i^+ + D_i^-}$

$其中 S_i 为得分，D_i^+ 为评价对象与最大值的距离，D_i^- 为评价对象与最小值的距离。$

我们继续帮助明星Kun选对象

明星 Kun 考虑了一下觉得光靠颜值和脾气可能考虑的还不够全面，就又加上了身高和体重两个指标，而且他认为身高 165 是最好，体重在 90 - 100 斤是最好。

候选人	颜值	脾气（争吵次数）	身高	体重
A	9	10	175	120
B	8	7	164	80
C	6	3	157	90

原始矩阵正向化

指标名称	指标特点	例子
极大型（效益型）指标	越大（多）越好	颜值、成绩、GDP 增速
极小型（成本型）指标	越小（少）越好	脾气、费用、坏品率、污染程度
中间型指标	越接近某个值越好	身高、水质量评估时的 PH 值
区间型指标	落在某个区间最好	体重、体温

将原始矩阵正向化，就是要将所有的指标类型统一转化为极大型指标。

指标名称	公式
极大型（效益型）指标	/
极小型（成本型）指标	$x^=max−x\hat{x} = max - x$ ， $x^\hat{x}$ 为转化后指标， $ma x$ 为指标最大值， $x$ 为指标值
中间型指标	${x_i\}$ 是一组中间型序列，最优值是 $xbestx_{\text{best}}$ ，正向化公式如下 $\max\left\{ \vert x_i - x_{\text{best}} \vert \right\}$ ， $x^i=1−∣xi−xbest∣M\hat{x}_i = 1 - \frac{\vert x_i - x_{\text{best}} \vert}{M}$
区间型指标	${x_i\}$ 是一组区间型序列，最佳区间为 $[a, b]$ ，正向化公式如下 $M = max\{a - min\{x_i\}, max\{x_i\} - b\}$ ， $x^i={1−a−xiM,xi<a1,a≤xi≤b1−xi−bM,xi>b\hat{x}_i = \begin{cases} 1 - \frac{a - x_i}{M}, & x_i < a \\ 1, & a \leq x_i \leq b \\ 1 - \frac{x_i - b}{M}, & x_i > b \end{cases}$

原始矩阵

候选人颜值脾气 (争吵次数) 身高 165 体重 90-100
A 9 10 175 120
B 8 7 164 80
C 6 3 157 90
正向化后的矩阵

候选人颜值脾气 (争吵次数) 身高体重
A 9 0 0 0
B 8 3 0.9 0.5
C 6 7 0.2 1
正向化矩阵标准化
- 标准化的目的是消除不同指标量纲的影响。
假设有 $n$ 个要评价的对象， $m$ 个评价指标（已正向化）构成的正向化矩阵如下：
$\begin{bmatrix} x_{11} & \cdots & x_{1m} \\ \vdots & \ddots & \vdots \\ x_{n1} & \cdots & x_{nm} \end{bmatrix}$

那么，对其标准化的矩阵记为 $Z$ ， $Z$ 中的每一个元素：
$zij=xij∑i=1nxij2z_{ij} = \frac{x_{ij}}{\sqrt{\sum_{i=1}^{n} x_{ij}^2}}$
（解释：每一个元素 $/$ $其所在列的元素的平方和\sqrt{其所在列的元素的平方和}$ ）
- 标准化后，还需给不同指标加上权重，采用的权重确定方法有层次分析法、熵权法、Delphi法、对数最小二乘法等。在这里认为各个指标的权重相同。

候选人	颜值	脾气(争吵次数)	身高	体重
A	9	0	0	0
B	8	3	0.9	0.5
C	6	7	0.2	1

$⇒\boldsymbol{\Rightarrow}$

候选人	颜值	脾气(争吵次数)	身高	体重
A	0.669	0	0	0
B	0.595	0.394	0.976	0.447
C	0.446	0.919	0.217	0.894

计算得分并归一化
- 上一步得到标准化矩阵 ( Z )
  $\begin{bmatrix} z_{11} & \cdots & z_{1m} \\ \vdots & \ddots & \vdots \\ z_{n1} & \cdots & z_{nm} \end{bmatrix}$

定义最大值
$Z^+ = (Z_1^+, Z_2^+, \dots, Z_m^+) = \big( \max\{z_{11}, z_{21}, \dots, z_{n1}\},\ \max\{z_{12}, z_{22}, \dots, z_{n2}\},\ \dots,\ \max\{z_{1m}, z_{2m}, \dots, z_{nm}\} \big) )$
- 定义最小值
  $Z^- = (Z_1^-, Z_2^-, \dots, Z_m^-) = \big( \min\{z_{11}, z_{21}, \dots, z_{n1}\},\ \min\{z_{12}, z_{22}, \dots, z_{n2}\},\ \dots,\ \min\{z_{1m}, z_{2m}, \dots, z_{nm}\} \big) )$
- 定义第 i(i=1,2,…,n) 个评价对象与最大值的距离
  $D_i^+ = \sqrt{\sum_{j=1}^{m} \big(Z_j^+ - z_{ij}\big)^2} )$
- 定义第 i(i=1,2,…,n) 个评价对象与最小值的距离
  $D_i^- = \sqrt{\sum_{j=1}^{m} \big(Z_j^- - z_{ij}\big)^2} )$
- 那么，我们可以计算得出第 i(i=1,2,…,n) 个评价对象未归一化的得分：
  $Si=Di−Di++Di−S_i = \frac{D_i^-}{D_i^+ + D_i^-}$
- 很明显 $\leq S_i \leq 1$ ，且 $S_i$ 越大 $D_i^+$ 越小，即越接近最大值
- 我们可以将得分归一化并换成百分制：
  $S~i=Si∑i=1nSi×100\tilde{S}_i = \frac{S_i}{\sum_{i=1}^{n} S_i} \times 100$

归一化后的矩阵

上一步标准化的矩阵

候选人颜值脾气（争吵次数）身高体重
A 0.669 0 0 0
B 0.595 0.394 0.976 0.447
C 0.446 0.919 0.217 0.894
$⇒\boldsymbol{\Rightarrow}$
归一化后

候选人得分
A 0.122
B 0.624
C 0.622
$⇒\boldsymbol{\Rightarrow}$
转换为百分制

候选人得分
A 8.9
B 45.7
C 45.5