逆波兰表达式求值

这是一道经典地使用栈来解决后缀表达式求解的题目。使用栈来求解后缀表达式的流程如下：

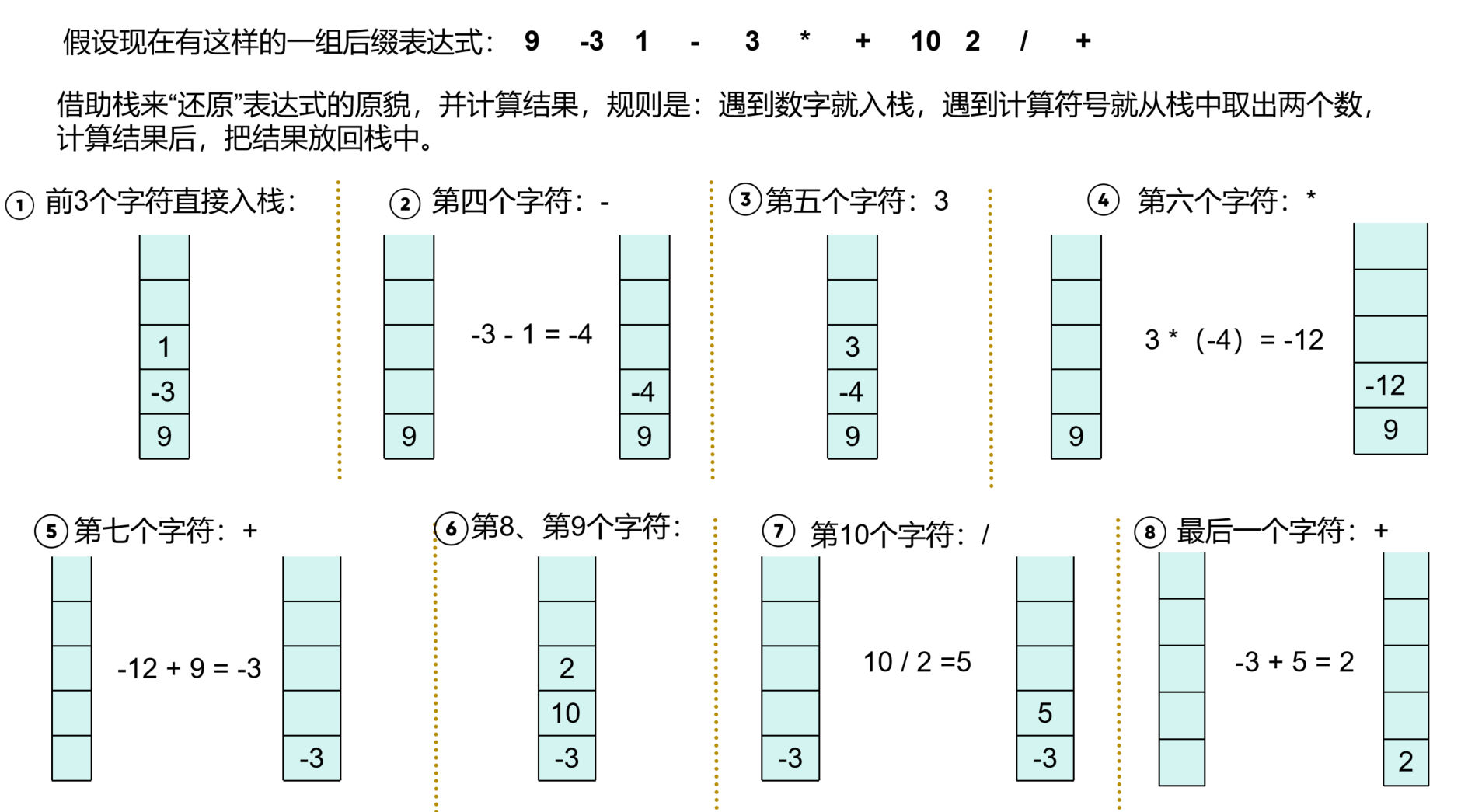
借助栈的结构，可以求解出原始表达式是：9 +（-3 - 1）* 3 + 10 / 2 = 2，在遵照规则过程中，还有些细节要注意：

1.   数字字符串如何转化为整数格式？尤其是负数。
2. 注意遇到计算符号时，从栈中出栈用于计算的两个数，对于减法和除法是有序的，被减数/被除数应该是按照原始的入栈顺序来确定，也就是先入栈的是被减数/被除数，所以先出栈的是减数/除数。

代码如下，因为考虑到耗时上的加速，所以直接使用字符数组来表示栈，栈顶通过数组长度这个变量来维护：

class Solution {
public:int getInt(string s){//如果字符串是计算符，返回201int num = 201;if(s.length()==1&&(s[0]=='-'||s[0]=='+'||s[0]=='*'||s[0]=='/')){num = 201;}//字符串是数字，则转化为int值else{if(s[0]=='-'){//这是一个负数num = 0;for(int i = 1;i<s.length();i++){num = 10 * num + s[i]-'0';}num = -num;}else{//非负数num = 0;for(int i=0;i<s.length();i++){num  = num *10 +s[i]-'0';}}}return num;}int evalRPN(vector<string>& tokens) {int num_stack[10001];int stack_cnt = 0;for(int i= 0;i<tokens.size();i++){if(getInt(tokens[i])==201){//遇到计算符，就两个数字出栈，计算结果，并把结果放回到栈中int num2 = num_stack[stack_cnt-1];stack_cnt--;int num1 = num_stack[stack_cnt-1];stack_cnt--;int res = 0;if(tokens[i]=="+"){res = num1+num2;}else if(tokens[i]=="-"){res = num1 - num2;}else if(tokens[i]=="*"){res = num1 * num2;}else if(tokens[i]=="/"){res = num1 / num2;}num_stack[stack_cnt++]=res;}else{//遇到数字就入栈num_stack[stack_cnt++]=getInt(tokens[i]);}}return num_stack[stack_cnt-1];}
};