@[toc]
0.引子:从非平衡热力学开始
1.架构简介
2.反向过程的具体推导与 DDPM 改进
摘要:扩散模型将非平衡热力学的“噪声注入—去噪逆转”理念注入生成建模中。DDPM(Denoising Diffusion Probabilistic Models)在 SD2015 的基础上,通过重参数化、损失简化、固定方差和网络架构优化等一系列改进,实现了更稳定的训练和更高质量的生成。本文将从物理直觉出发,面向概率论初学者详细推导每一步公式,在一些重要概念处专门附上实例,确保新手友好。
0 引子:从非平衡热力学开始
想象一滴墨水滴入静水,墨滴在水中扩散,最终呈现均匀的淡灰色。扩散模型正借鉴这一物理过程:
- 前向扩散(Forward):逐步向样本中注入噪声,如同墨滴不断散开;
- 反向去噪(Reverse):学习如何倒放这个过程,一步步去除噪声,重现原始图像。
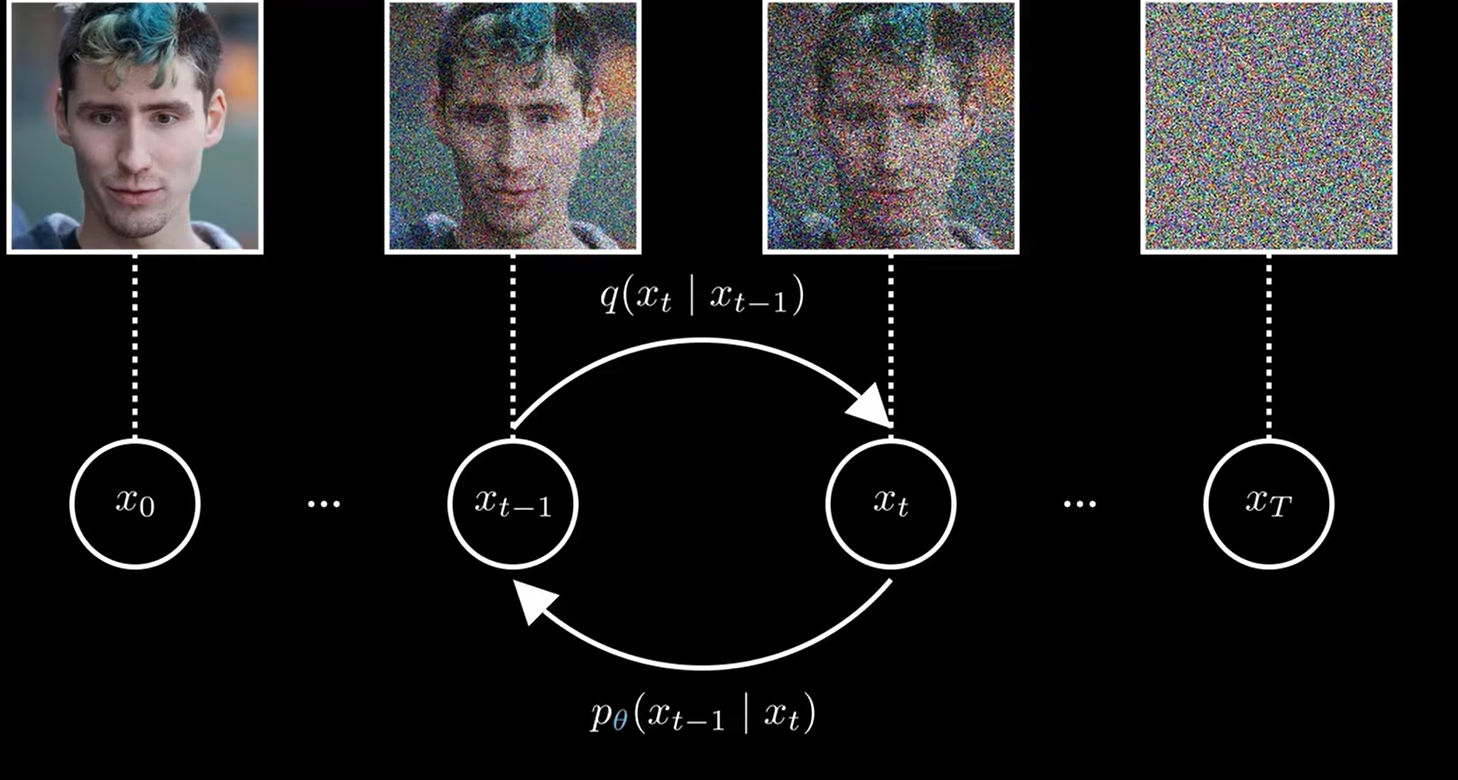
2015 年,Sohl-Dickstein 等人提出了首个非平衡热力学生成框架:Deep Unsupervised Learning using Nonequilibrium Thermodynamics;2020 年,Ho 等人优化为 DDPM:Denoising Diffusion Probabilistic Models。引入重参数化、损失简化和架构改进,使模型更易训练且样本质量提升。
本文图片主要出自:Diffusion Models: DDPM | Generative AI Animated
1 架构简介
1.1 前向扩散与反向去噪的直观解读
前向扩散:
从真实样本 x0x_0x0 出发,在每一步 ttt 以方差 βt\beta_tβt 递增的方式添加高斯噪声:
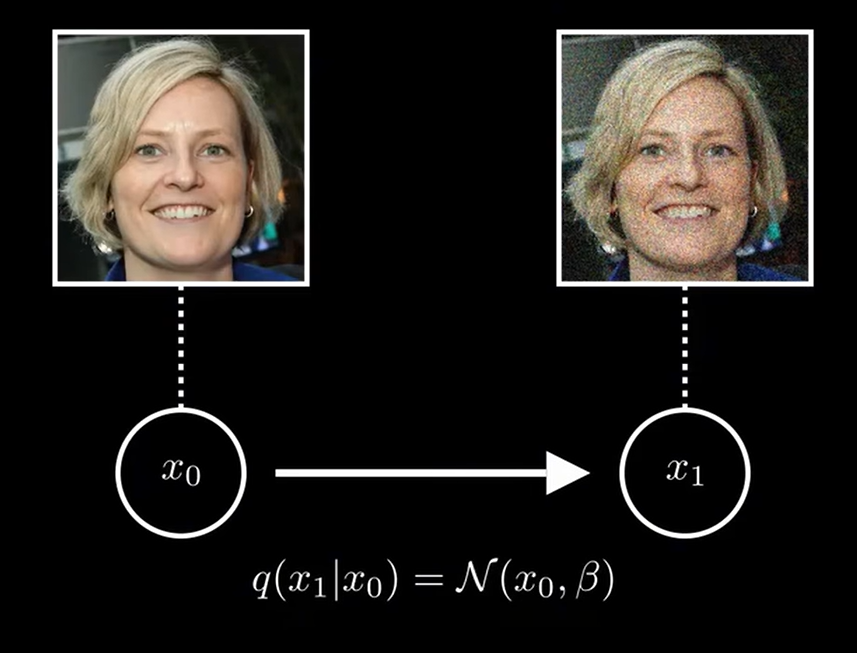
如果我们只加一步噪声,那么公式为:
x1=x0+βϵϵ∼N(0,1)x_1 = x_0 +\beta \epsilon \quad \epsilon \sim \mathcal{N}(0,1) x1=x0+βϵϵ∼N(0,1)
β\betaβ事实上就是一个控制加噪声强度的超参数。考虑到我们加噪声实际上以及都是不断地外套一个线性函数,所以第ttt步实际上可以表示为:
xt=x0+tβϵϵ∼N(0,1)x_t = x_0 +t\beta \epsilon \quad \epsilon \sim \mathcal{N}(0,1) xt=x0+tβϵϵ∼N(0,1)
那么对应的图像实际上也就变成了:

不过,按照上述加噪声的方式,我们得到的并非N(0,1)\mathcal{N}(0,1)N(0,1)的标准高斯分布,所以我们在加噪声时需要来一点小小的技巧:
q(xt∣xt−1)=1−βxt−1+βϵ=N(xt;1−βtxt−1,βtI).q(x_t\mid x_{t-1}) = \sqrt{1-\beta} x_{t-1} + \beta \epsilon =\mathcal{N}\bigl(x_t;\sqrt{1-\beta_t}\,x_{t-1},\;\beta_t I\bigr). q(xt∣xt−1)=1−βxt−1+βϵ=N(xt;1−βtxt−1,βtI).
若表示为xt,x0x_t,x_0xt,x0的关系:
q(xt∣x0)=αˉtx0+(1−αˉtt)⋅ϵq(x_ t∣x_ 0)= \bar{\alpha}_tx_0 +(1− \bar{\alpha}_tt)⋅ϵ q(xt∣x0)=αˉtx0+(1−αˉtt)⋅ϵ
αˉ=(1−β)t\bar{\alpha} = (1-\beta)^t αˉ=(1−β)t
注:这不是唯一的技巧,但是为论文中采用的技巧
提要:
可能有许多读者在一开始会困惑: “为什么图像能被表示为概率公式”?我们可以从 图像的本质、噪声添加的过程两个角度拆解,结合公式 q(xt∣xt−1)=N(xt;1−βtxt−1,βtI)q(x_t \mid x_{t-1}) = \mathcal{N}\bigl(x_t;\sqrt{1-\beta_t}\,x_{t-1},\;\beta_t I\bigr)q(xt∣xt−1)=N(xt;1−βtxt−1,βtI)逐层解释
- 图像的本质:高维随机变量计算机中的图像,本质是高维像素值的集合(比如 256×256 图像有 256×256×3=196608256 \times 256 \times 3 = 196608256×256×3=196608 个像素)。每个像素的取值(如 RGB 或灰度值)可以看作连续随机变量(缩放到 [−1,1][-1,1][−1,1] 后更便于计算)。因此,一张图像可以被视为 “高维随机变量的一个样本” —— 就像抛一次骰子得到一个数字,生成一张图像相当于从 “所有可能图像的分布” 中采样一次。
- 正向加噪:用高斯分布建模 “图像退化”扩散模型的正向过程是 “逐步给图像加噪声,让其从清晰变模糊”。每一步加噪的本质是:给每个像素的取值叠加随机扰动(噪声)。公式拆解:
q(xt∣xt−1)N(xt;1−βtxt−1⏟均值,derbraceβtI方差)q(x_t \mid x_{t-1}) \mathcal{N}\bigl(x_t;\ \underbrace{\sqrt{1-\beta_t}\,x_{t-1}}_{\text{均值}},\ derbrace{\beta_t I}_{\text{方差}}\bigr)q(xt∣xt−1)N(xt; 均值1−βtxt−1, derbraceβtI方差)
而均值项
1−βtxt−1\sqrt{1-\beta_t}\,x_{t-1}1−βtxt−1:
表示 “前一步图像 xt−1x_{t-1}xt−1 缩放后的结果”。因为加噪会让图像 “变淡”(像素值偏离原始值),所以用 1−βt\sqrt{1-\beta_t}1−βt缩放
例子:假设 xt−1x_{t-1}xt−1 是清晰猫图的某个像素(值为 0.50.50.5),βt=0.01\beta_t = 0.01βt=0.01(加少量噪声),则均值为 1−0.01×0.5≈0.497\sqrt{1-0.01} \times 0.5 \approx 0.4971−0.01×0.5≈0.497(像素值略降低,图像开始模糊)。方差项 βtI\beta_t IβtI:I 是单位矩阵,意味着每个像素的噪声是独立的高斯分布(不同像素的噪声互不影响)。βt\beta_tβt 控制噪声的 “强度”(越大,噪声越强,图像越模糊)。
反向去噪:
理论上说,在反向部分,我们完全可以将前向部分的xt,xt−1x_t,x_{t-1}xt,xt−1交换位置得到真实后验再计算即可。但事实上真实后验
q(xt−1∣xt,x0)=q(xt∣xt−1)q(xt−1∣x0)q(xt∣x0)q(x_{t-1}\mid x_t,x_0) = \frac{q(x_t\mid x_{t-1})\,q(x_{t-1}\mid x_0)}{q(x_t\mid x_0)} q(xt−1∣xt,x0)=q(xt∣x0)q(xt∣xt−1)q(xt−1∣x0)
无法解析,因为它依赖于对高维分布 q(x0)q(x_0)q(x0) 的复杂积分。不过,为什么 q(xt−1∣xt,x0)q(x_{t-1}\mid x_t,x_0)q(xt−1∣xt,x0) 难以解析?
假设 x0x_0x0 是一张 64×6464\times6464×64 的彩色图像(维度 64×64×3=1228864\times64\times3=1228864×64×3=12288),
- 分子是可以利用前向过程表示,但是分母要计算
q(xt∣x0)=∫q(xt∣xt−1)q(xt−1∣x0)dxt−1,q(x_t\mid x_0) = \int q(x_t\mid x_{t-1})\,q(x_{t-1}\mid x_0)\,\mathrm{d}x_{t-1}, q(xt∣x0)=∫q(xt∣xt−1)q(xt−1∣x0)dxt−1,
需要对 12288 维空间做积分。 - 这样的高维积分既没有解析解,也无法通过常规模拟快速收敛(“维度诅咒”)。
因此,我们不能直接写出 q(xt−1∣xt,x0)q(x_{t-1}\mid x_t,x_0)q(xt−1∣xt,x0) 的明确公式,也无法精确求值。
于是,我们引入神经网络 pθp_\thetapθ ,只需让网络根据大量样本拟合这一映射,无需解析积分,就能实现高效去噪。
引入神经网络
用参数化分布
pθ(xt−1∣xt)=N(xt−1;μθ(xt,t),Σθ(t))p_\theta(x_{t-1}\mid x_t) = \mathcal{N}\bigl(x_{t-1};\mu_\theta(x_t,t),\,\Sigma_\theta(t)\bigr) pθ(xt−1∣xt)=N(xt−1;μθ(xt,t),Σθ(t))
来近似上述真实后验,θ\thetaθ 为网络权重,通过最小化损失自动学习。
那么,具体是怎么训练该神经网络的呢?待我们在下一节推导损失函数后再揭晓答案。
改进点:SD2015 的网络既要预测均值 μ~t\tilde\mu_tμ~t 又要输出方差 β~t\tilde\beta_tβ~t,任务较重;DDPM 在后续简化步骤中将方差固定,大大减轻网络负担。
1.2 数学表达一览
-
前向整体:
q(x1:T∣x0)=∏t=1Tq(xt∣xt−1).q(x_{1:T}\mid x_0) = \prod_{t=1}^T q(x_t\mid x_{t-1}). q(x1:T∣x0)=t=1∏Tq(xt∣xt−1). -
反向整体:
pθ(x0:T)=p(xT)∏t=1Tpθ(xt−1∣xt).p_\theta(x_{0:T}) = p(x_T)\prod_{t=1}^T p_\theta(x_{t-1}\mid x_t). pθ(x0:T)=p(xT)t=1∏Tpθ(xt−1∣xt). -
采样 vs. 训练:
- 采样:从 xT∼N(0,I)x_T\sim \mathcal{N}(0,I)xT∼N(0,I) 逆向采样至 x0x_0x0;
- 训练:最大化对数似然 logpθ(x0)\log p_\theta(x_0)logpθ(x0),或等价地最小化其 ELBO(证据下界)。在一节大家就明白了。
2 反向过程 pθp_\thetapθ 的具体推导与 DDPM 改进
2.1 变分下界的起点
首先,我们应该明确:为了训练出能够完成去噪与生成任务的神经网络,我们的目标函数是最大化模型对真实数据的似然,也就是
maxθlogpθ(x0).\max_\theta\;\log p_\theta(x_0)\,. θmaxlogpθ(x0).
-
统计视角:最大化 logpθ(x0)\log p_\theta(x_0)logpθ(x0) 等价于最小化负对数似然(NLL),也就是说,我们希望模型对观测到的数据给出尽可能高的“信心”值。如果读者对于概率统计的知识有些生疏了的话,可以看看下面具体的举例:
例子:伯努利分布下的硬币抛掷
- 设我们使用参数 θ\thetaθ 表示“正面朝上”的概率,概率模型为
pθ(x)=θx(1−θ)1−x,x∈{0,1}.p_\theta(x) = \theta^x (1-\theta)^{1-x},\quad x\in\{0,1\}. pθ(x)=θx(1−θ)1−x,x∈{0,1}. - 如果观测到一组抛掷结果 {1,0,1,1,0}\{1,0,1,1,0\}{1,0,1,1,0}(1 表示正面,0 表示反面),则该组数据的对数似然为
logpθ({xi})=∑i=15[xilogθ+(1−xi)log(1−θ)].\log p_\theta(\{x_i\}) = \sum_{i=1}^5 \bigl[x_i\log\theta + (1-x_i)\log(1-\theta)\bigr]. logpθ({xi})=i=1∑5[xilogθ+(1−xi)log(1−θ)]. - 最大化这段式子,就是求解最佳 θ\thetaθ,使得模型预测的“正面概率”最贴合实际观测。具体地,上式在 θ=∑xi5=0.6\theta=\tfrac{\sum x_i}{5}=0.6θ=5∑xi=0.6 处取得最大值,这也恰好是观测中正面出现的频率。
通过这个过程,我们看到:最大化 logpθ(x0)\log p_\theta(x_0)logpθ(x0) 就像让模型“学习”数据的真实分布,用最合理的参数去解释观测结果。
- 设我们使用参数 θ\thetaθ 表示“正面朝上”的概率,概率模型为
-
物理视角:在非平衡热力学框架下,−logpθ(x0)-\log p_\theta(x_0)−logpθ(x0) 可被解读为模型“解释”数据所需的自由能(或“做功”),最低自由能对应最自然的物理过程。
然而,logpθ(x0)\log p_\theta(x_0)logpθ(x0) 涉及对所有中间变量 x1:Tx_{1:T}x1:T 的积分
logpθ(x0)=log∫pθ(x0:T)dx1:T,\log p_\theta(x_0) = \log \int p_\theta(x_{0:T})\,\mathrm{d}x_{1:T}\,, logpθ(x0)=log∫pθ(x0:T)dx1:T,
直接计算几乎不可行。因为这里的是的,这里的 dx1:T\mathrm{d}x_{1:T}dx1:T 就是
dx1dx2⋯dxT\mathrm{d}x_1\,\mathrm{d}x_2\,\cdots\,\mathrm{d}x_T dx1dx2⋯dxT
相当于我们需要对所有可能的路径积分
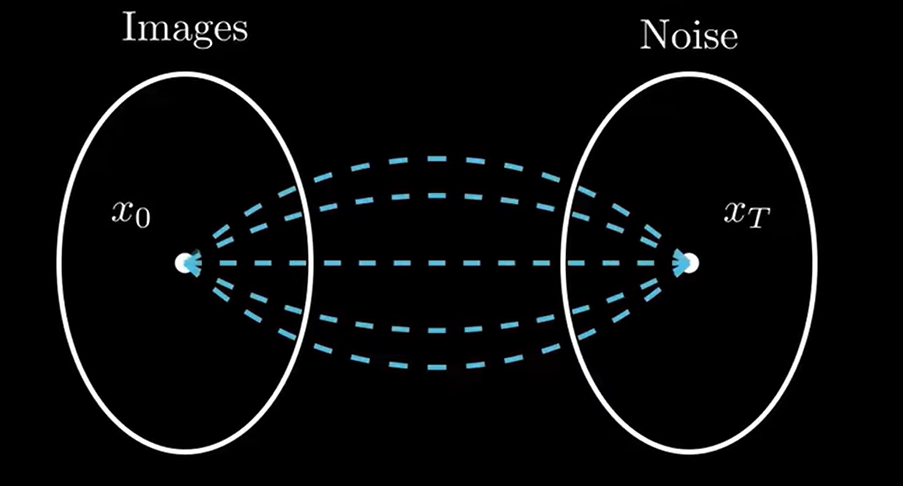
P.S.:如果不太理解,可以参考本小节结束后的具体举例。
我们借助以下推导,得到一个可优化的下界——ELBO(证据下界):
-
引入完整分布
logpθ(x0)=log∫pθ(x0:T)dx1:T.\log p_\theta(x_0) = \log \int p_\theta(x_{0:T})\,\mathrm{d}x_{1:T}. logpθ(x0)=log∫pθ(x0:T)dx1:T. -
乘以并除以任意分布 q(x1:T∣x0)q(x_{1:T}\mid x_0)q(x1:T∣x0)
注意:这是一个常见的、并且在其它ML模型的数学原理的推导中也会见到的小技巧。
logpθ(x0)=log∫q(x1:T∣x0)pθ(x0:T)q(x1:T∣x0)dx1:T.\log p_\theta(x_0) = \log \int q(x_{1:T}\mid x_0)\,\frac{p_\theta(x_{0:T})}{q(x_{1:T}\mid x_0)} \,\mathrm{d}x_{1:T}. logpθ(x0)=log∫q(x1:T∣x0)q(x1:T∣x0)pθ(x0:T)dx1:T. -
将积分写成期望
logpθ(x0)=logEq(x1:T∣x0)[pθ(x0:T)q(x1:T∣x0)].\log p_\theta(x_0) = \log \mathbb{E}_{q(x_{1:T}\mid x_0)}\Bigl[ \tfrac{p_\theta(x_{0:T})}{q(x_{1:T}\mid x_0)} \Bigr]. logpθ(x0)=logEq(x1:T∣x0)[q(x1:T∣x0)pθ(x0:T)]. -
应用 Jensen 不等式(log\loglog 为凹函数)
logE[Y]≥E[logY]⟹logpθ(x0)≥Eq(x1:T∣x0)[logpθ(x0:T)q(x1:T∣x0)].\log \mathbb{E}[Y] \;\ge\; \mathbb{E}[\log Y] \quad\Longrightarrow\quad \log p_\theta(x_0) \;\ge\; \mathbb{E}_{q(x_{1:T}\mid x_0)}\Bigl[ \log \tfrac{p_\theta(x_{0:T})}{q(x_{1:T}\mid x_0)} \Bigr]. logE[Y]≥E[logY]⟹logpθ(x0)≥Eq(x1:T∣x0)[logq(x1:T∣x0)pθ(x0:T)]. -
取相反数,得到 ELBO
−logpθ(x0)≤−Eq(x1:T∣x0)[logpθ(x0:T)q(x1:T∣x0)].-\log p_\theta(x_0) \;\le\; -\mathbb{E}_{q(x_{1:T}\mid x_0)}\Bigl[ \log \tfrac{p_\theta(x_{0:T})}{q(x_{1:T}\mid x_0)} \Bigr]. −logpθ(x0)≤−Eq(x1:T∣x0)[logq(x1:T∣x0)pθ(x0:T)].
至此,我们将原本难以直接计算的 logpθ(x0)\log p_\theta(x_0)logpθ(x0),转化为了可以通过采样 q(x1:T∣x0)q(x_{1:T}\mid x_0)q(x1:T∣x0) 并分步优化的 ELBO 目标,便于利用梯度下降训练网络参数 θ\thetaθ。
补充:
具体例子:两步高斯链
假设我们有三个随机变量按下面的马尔可夫链生成:
- 先采样 x2∼N(0,1)x_2\sim\mathcal{N}(0,1)x2∼N(0,1)。
- 再采样 x1∣x2∼N(x2,1)x_1\mid x_2\sim\mathcal{N}(x_2,\,1)x1∣x2∼N(x2,1)。
- 最后采样 x0∣x1∼N(x1,1)x_0\mid x_1\sim\mathcal{N}(x_1,\,1)x0∣x1∼N(x1,1)。
则联合分布为
pθ(x0,x1,x2)=p(x2)p(x1∣x2)p(x0∣x1)=N(x2;0,1)N(x>1;x2,1)N(x0;x1,1).p_\theta(x_0,x_1,x_2) = p(x_2)\,p(x_1\mid x_2)\,p(x_0\mid x_1) = \mathcal{N}(x_2;0,1)\,\mathcal{N}(x>_1;x_2,1)\,\mathcal{N}(x_0;x_1,1). pθ(x0,x1,x2)=p(x2)p(x1∣x2)p(x0∣x1)=N(x2;0,1)N(x>1;x2,1)N(x0;x1,1).
我们关心的边缘分布 (p_\theta(x_0)) 就是对所有中间状态 (x_1) 和 (x_2) 同时积分:
pθ(x0)=∫−∞∞∫−∈>fty∞pθ(x0,x1,x2)dx>1dx2.p_\theta(x_0) = \int_{-\infty}^{\infty}\!\int_{-\in>fty}^{\infty} p_\theta(x_0,x_1,x_2)\,\mathrm{d}x>_1\,\mathrm{d}x_2. pθ(x0)=∫−∞∞∫−∈>fty∞pθ(x0,x1,x2)dx>1dx2.
- 这里既要“遍历”所有可能的 (x_1) 值,
- 也要“遍历”所有可能的 (x_2) 值,
- 最终把这两个积分都做完,才能得到只含 (x_0) 的边缘概率。
正是因为这种“对每一条从 x0x_0x0 回溯到 xTx_TxT 的所有中间路径(即所有中间变量组合)都要积分”导致计算量巨大,难以直接求解,才需要我们引入变分下界(ELBO)或用神经网络去近似。
2.2 *链式分解为 KL 项
展开 ELBO 得到(该部分推导相对冗杂,可见原论文附录)
L=LT+∑t=2TLt−1+L0,L = L_T + \sum_{t=2}^T L_{t-1} + L_0, L=LT+t=2∑TLt−1+L0,
其中:
-
LT=DKL[q(xT∣x0)∥p(xT)],L_T = D_{\mathrm{KL}}\bigl[q(x_T\mid x_0)\,\|\,p(x_T)\bigr],LT=DKL[q(xT∣x0)∥p(xT)],
我们可以发现,该项中并不含有神经网络的参数θ\thetaθ,所以在优化过程中可以不必考虑。 -
L0=−Eq(x1∣x0)[logpθ(x0∣x1)].L_0 = -\mathbb{E}_{q(x_1\mid x_0)}\bigl[\log p_\theta(x_0\mid x_1)\bigr].L0=−Eq(x1∣x0)[logpθ(x0∣x1)].
这一项反映的实际上是模型最后一步的还原的过程。假如我们的还原步骤很长很长,显然最后一步的影响微乎其微,故可以忽略。 -
Lt−1=Eq(xt∣x0)[DKL(q(xt−1∣xt,x0)∥pθ(xt−1∣xt))],L_{t-1} = \mathbb{E}_{q(x_t\mid x_0)}\!\bigl[D_{\mathrm{KL}}\bigl(q(x_{t-1}\mid x_t,x_0)\,\|\,p_\theta(x_{t-1}\mid x_t)\bigr)\bigr],Lt−1=Eq(xt∣x0)[DKL(q(xt−1∣xt,x0)∥pθ(xt−1∣xt))],
于是我们最终的目标函数就等价于最小化上式。接下来我们对上式的含义进行一个拆解: 这其实是在说:对每一个“噪声等级”ttt,我们都要让模型给出的去噪分布
pθ(xt−1∣xt)p_\theta(x_{t-1}\mid x_t)pθ(xt−1∣xt)
尽量贴近真实后验
q(xt−1∣xt,x0).q(x_{t-1}\mid x_t,x_0)\,. q(xt−1∣xt,x0).-
内层 KL 散度含义
DKL(q∥pθ)=∫q(xt−1∣xt,x0)logq(xt−1∣xt,x0)pθ(xt−1∣xt)dxt−1.D_{\mathrm{KL}}\bigl(q\,\|\,p_\theta\bigr) = \int q(x_{t-1}\mid x_t,x_0)\;\log\frac{q(x_{t-1}\mid x_t,x_0)}{p_\theta(x_{t-1}\mid x_t)}\;\mathrm{d}x_{t-1}. DKL(q∥pθ)=∫q(xt−1∣xt,x0)logpθ(xt−1∣xt)q(xt−1∣xt,x0)dxt−1.- 这里的“logqpθ\log\frac{q}{p_\theta}logpθq”衡量了真实后验与模型后验在每一个可能的 xt−1x_{t-1}xt−1 上的“距离”。
- 如果两者完全相同,KL 为 0;否则越大,说明差异越大,网络需要更努力地学习。
-
外层期望的作用
Eq(xt∣x0)[⋅]\mathbb{E}_{q(x_t\mid x_0)}[\;\cdot\;]Eq(xt∣x0)[⋅]
表示:我们不是只对某一个特定的xtx_txt 做对比,而是对所有可能的“噪声样本” xtx_txt 取平均。
换句话说,模型要在整个前向扩散轨迹上,对每一个噪声等级都表现良好。 -
关于真实后验与训练方法
再次指出可能混引起混淆的一点:细心的同学可能会发现一点:如果我们已知了去噪过程$q(x_{t-1}\mid x_t,x_0) ,那为什么还需要使用神经网络?事实上,我们能且仅能在训练的过程中知道,那为什么还需要使用神经网络?事实上,我们能且仅能在训练的过程中知道,那为什么还需要使用神经网络?事实上,我们能且仅能在训练的过程中知道q(x_{t-1}\mid x_t,x_0),因为在该过程中我们是有原始图像,因为在该过程中我们是有原始图像,因为在该过程中我们是有原始图像x_0$的。
在推理过程,我们相当于只有一团混沌的噪声,不可能解析地求出q(xt−1∣xt,x0)q(x_{t-1}\mid x_t,x_0)q(xt−1∣xt,x0)。而我们的目标,正是利用DKL[q(xT∣x0)∥p(xT)],D_{\mathrm{KL}}\bigl[q(x_T\mid x_0)\,\|\,p(x_T)\bigr],DKL[q(xT∣x0)∥p(xT)],,去使 pθ(xt−1∣xt)p_\theta(x_{t-1}\mid x_t)pθ(xt−1∣xt)
尽量贴近真实后验q(xt−1∣xt,x0)q(x_{t-1}\mid x_t,x_0)q(xt−1∣xt,x0).
-
KL 散度 DKL[P∥Q]D_{\mathrm{KL}}[P\|Q]DKL[P∥Q] 衡量分布 PPP 与 QQQ 的差异。最小化 KL 即逼近真实后验。
2.3 真后验 & 参数化模型
在上一节我们看到,每一步的 ELBO 包含
Lt−1=Eq(xt∣x0)[DKL(q(xt−1∣xt,x0)∥pθ(xt−1∣xt))].L_{t-1} = \mathbb{E}_{q(x_t\mid x_0)}\! \bigl[D_{\mathrm{KL}}(q(x_{t-1}\mid x_t,x_0)\,\|\,p_\theta(x_{t-1}\mid x_t))\bigr]. Lt−1=Eq(xt∣x0)[DKL(q(xt−1∣xt,x0)∥pθ(xt−1∣xt))].
要最小化它,首先得知道“真实后验” (xt−1∣xt,x0)(x_{t-1}\mid x_t,x_0)(xt−1∣xt,x0)的形式。经过一番高斯链式推导(详见附录),我们可以得到:
q(xt−1∣xt,x0)=N(xt−1;μ~t(xt,x0),β~tI),q(x_{t-1}\mid x_t,x_0) = \mathcal{N}\bigl(x_{t-1};\,\tilde\mu_t(x_t,x_0),\;\tilde\beta_t I\bigr), q(xt−1∣xt,x0)=N(xt−1;μ~t(xt,x0),β~tI),
其中
$$
\tilde\mu_t
= \frac{\sqrt{\bar\alpha_{t-1}};\beta_t}{1-\bar\alpha_t},x_0
- \frac{\sqrt{\alpha_t},(1-\bar\alpha_{t-1})}{1-\bar\alpha_t},x_t,
\quad
\tilde\beta_t
= \frac{1-\bar\alpha_{t-1}}{1-\bar\alpha_t};\beta_t.
$$
接下来,我们让模型后验pθ(xt−1∣xt)p_\theta(x_{t-1}\mid x_t)pθ(xt−1∣xt)也服从高斯分布:
pθ(xt−1∣xt)=N(xt−1;μθ(xt,t),Σθ(t)).p_\theta(x_{t-1}\mid x_t) = \mathcal{N}\bigl(x_{t-1};\,\mu_\theta(x_t,t),\;\Sigma_\theta(t)\bigr). pθ(xt−1∣xt)=N(xt−1;μθ(xt,t),Σθ(t)).
为了简化采样与训练,DDPM 进一步固定方差 Σθ(t)=βtI\Sigma_\theta(t)=\beta_tIΣθ(t)=βtI,也就是只让网络去学习均值 μθ\mu_\thetaμθ 的移动。
此时,每步的 KL 散度化为一个均方误差项(省略常数):
DKL(N(μ~t,β~t)∥N(μθ,βt))∝12βt∥μθ(xt,t)−μ~t(xt,x0)∥2.D_{\mathrm{KL}}(\mathcal{N}(\tilde\mu_t,\tilde\beta_t)\,\|\, \mathcal{N}(\mu_\theta,\beta_t)) \;\propto\; \frac{1}{2\beta_t}\,\bigl\|\mu_\theta(x_t,t)-\tilde\mu_t(x_t,x_0)\bigr\|^2. DKL(N(μ~t,β~t)∥N(μθ,βt))∝2βt1μθ(xt,t)−μ~t(xt,x0)2.
于是,我们的去噪目标简化为:
Lt−1=Eq(xt∣x0)[12βt∥μθ(xt,t)−μ~t(xt,x0)∥2].L_{t-1} \;=\; \mathbb{E}_{q(x_t\mid x_0)}\!\Bigl[\, \tfrac{1}{2\beta_t}\,\bigl\|\mu_\theta(x_t,t)-\tilde\mu_t(x_t,x_0)\bigr\|^2 \Bigr]. Lt−1=Eq(xt∣x0)[2βt1μθ(xt,t)−μ~t(xt,x0)2].
2.4 均值的闭式 & 重参数化到 ε
为了让训练更高效,先写出μ~t\tilde\mu_tμ~t 的闭式表达:
μ~t(xt,x0)=1αt(xt−1−αt1−αˉtϵ),xt=αˉtx0+1−αˉtϵ,ϵ∼N(0,I).\tilde\mu_t(x_t,x_0)= \frac{1}{\sqrt{\alpha_t}}\Bigl(x_t- \tfrac{1-\alpha_t}{\sqrt{1-\bar\alpha_t}}\,\epsilon\Bigr),\quad x_t = \sqrt{\bar\alpha_t}\,x_0 + \sqrt{1-\bar\alpha_t}\,\epsilon,\;\epsilon\sim\mathcal{N}(0,I). μ~t(xt,x0)=αt1(xt−1−αˉt1−αtϵ),xt=αˉtx0+1−αˉtϵ,ϵ∼N(0,I).
- 这里的 ϵ\epsilonϵ 就是“前向过程中注入”的噪声,重参数化技巧将随机性都集中到它身上。
将 μ~t\tilde\mu_tμ~t 代入前面那步 MSE,我们得到:
∥μθ(xt,t)−μ~t∥2=∥μθ(xt,t)−1αt(xt−1−αt1−αˉtϵ)∥2.\|\mu_\theta(x_t,t)-\tilde\mu_t\|^2= \Bigl\|\mu_\theta(x_t,t)- \tfrac{1}{\sqrt{\alpha_t}}\bigl(x_t - \tfrac{1-\alpha_t}{\sqrt{1-\bar\alpha_t}}\,\epsilon\bigr) \Bigr\|^2. ∥μθ(xt,t)−μ~t∥2=μθ(xt,t)−αt1(xt−1−αˉt1−αtϵ)2.
再结合系数 12βt\tfrac1{2\beta_t}2βt1和对 ϵ\epsilonϵ的期望,就能证明等价于:
Lt−1∝Ex0,ϵ,t[∥ϵ−ϵθ(xt,t)∥2],L_{t-1}\propto\mathbb{E}_{x_0,\epsilon,t}\bigl[\|\epsilon-\epsilon_\theta(x_t,t)\|^2\bigr], Lt−1∝Ex0,ϵ,t[∥ϵ−ϵθ(xt,t)∥2],
其中我们定义
ϵθ(xt,t):=αˉtμθ(xt,t)−αtxt×1−αˉt1−αt,\epsilon_\theta(x_t,t):= \sqrt{\bar\alpha_t}\,\mu_\theta(x_t,t)- \sqrt{\alpha_t}\,x_t \;\times\;\frac{\sqrt{1-\bar\alpha_t}}{1-\alpha_t}, ϵθ(xt,t):=αˉtμθ(xt,t)−αtxt×1−αt1−αˉt,
简化后直接让网络预测 ϵ\epsilonϵ,大大提高了训练稳定性和效果。
2.5 SD2015 的原始损失推导
回顾 SD2015,在没有重参数化之前,模型直接学习 (\mu_\theta) 和 (\Sigma_\theta),并按变分界逐步最小化:
Lt−1SD=Eq(xt,xt−1∣x0)[−logpθ(xt−1∣xt)]=E[βt22β~tαt(1−αˉt)∥xt−1−μ~t∥2],L_{t-1}^\text{SD} = \mathbb{E}_{q(x_t,x_{t-1}\mid x_0)}\Bigl[ -\log p_\theta(x_{t-1}\mid x_t) \Bigr] = \mathbb{E}\Bigl[\tfrac{\beta_t^2}{2\,\tilde\beta_t\,\alpha_t\,(1-\bar\alpha_t)} \|x_{t-1}-\tilde\mu_t\|^2 \Bigr], Lt−1SD=Eq(xt,xt−1∣x0)[−logpθ(xt−1∣xt)]=E[2β~tαt(1−αˉt)βt2∥xt−1−μ~t∥2],
其中每步的权重
βt22β~tαt(1−αˉt)\tfrac{\beta_t^2}{2\,\tilde\beta_t\,\alpha_t\,(1-\bar\alpha_t)}2β~tαt(1−αˉt)βt2
随 ttt 变化,导致训练中需要精心调参且收敛不稳。DDPM 的一系列改进,正是为了解决这一痛点。
2.6 总结
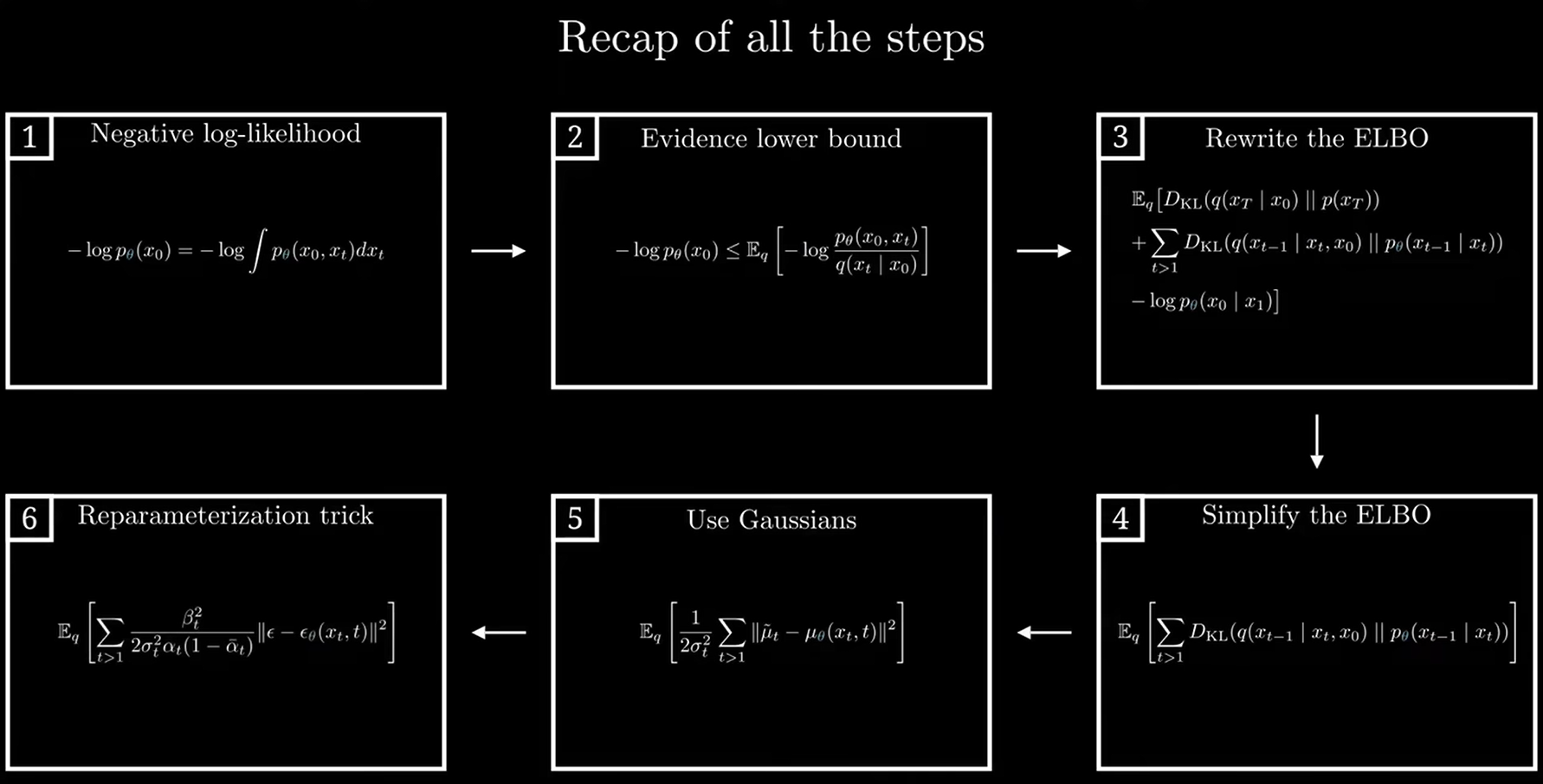

)




 的用法与实战案例)










)

