【题目链接】

ybt 1553：【例 2】暗的连锁

【题目考点】

1. 树上差分：边差分

类似对差分序列进行修改可以完成对原序列的区间修改。对树上边差分进行修改可以完成对树上一条路径中所有边的边权进行修改。
一条边的差分值为该边的权值减去该边连接的深度较大结点向孩子连出的所有边的权值加和。一般将边权值记录在该边连接的深度较大的结点中，虽然每个结点对应一个权值，实际表示的是该结点到其双亲的边的权值。
设差分数组$d$，$d_u$表示u到u的双亲边的权值减去 所有u到u的孩子边的权值的和 的差值。实际为结点u保存的权值减去所有u的孩子结点保存的权值的加和。
使树上路径(x, y)中所有边的权值都增加v，那么x、y到双亲的边的权值增加v，没有x、y到孩子的边，所以$d_x$与$d_y$都增加v。$LCA(x,y)$到孩子的边有两条，都增加v，而$LCA(x,y)$到其双亲的边的权值没有增加，因此$d_{LCA(x,y)}$减少$2v$。
因此对树上从x到y的路径上每条边都增加v的操作，对差分数组$d$的影响为：
$d_x=d_x+v,d_y=d_y+v,d_{LCA(x,y)}=d_{LCA(x,y)}-2v$

从根结点出发进行dfs，将每个结点所有孩子的权值加和，再加上当前结点的差分值，即为当前结点表示的权值，即当前结点到其双亲结点的边的权值。

【解题思路】

无向图有n个结点，的主要边有n-1条，而且任意两结点之间都存在一条由主要边构成的路径，即该图是连通图。
连通图有n个结点，n-1条边，那么该图是树。
接下来还有m条附加边，默认附加边和主要边不会重合。
目标是想通过切断一条主要边和一条附加边来使整个图不连通。
假设存在一条从结点A到结点B的附加边，在树上一定存在一条从结点A到结点B的路径，再加上附加边(A,B)，就会形成一个环。需要切掉树上从A到B路径上的一条主要边，以及(A,B)这一条附加边，才能使这个图不连通。
假设树上从A到B的路径上经过了边(C,D)。
现在假设存在另一个附加边(X,Y)，树上从X到Y的路径上也经过了边(C,D)。
那么即便去掉边(C,D)，从结点C到结点D也存在至少两条路径，接下来再切断哪条附加边，整个图仍然是连通的。

因此，每个附加边都与主要边构成的树形成了环。可以统计树上每条边参与构成环的数量。设边权的概念为该边参与构成了几个由主要边与附加边构成的环。
假设存在附加边(A, B)，就可以认为在树上从A到B的路径每条边的边权增加1。
遍历所有附加边，每条附加边都会使树上一条路径上每条边增加边权1，最后统计所有主要边的边权。该过程可以通过树上边差分方法完成。
遍历所有主要边：

• 如果一条主要边的权值为0，那么没有环经过这条边。切断该主要边后，整个图已经不连通了，再切断任意附加边都可以完成任务，方案数为附加边的数量m，切断边的方案数增加m。
• 如果一条主要边的权值为1，那么存在一条附加边和树形成的环经过了这条主要边。此时可以切断当前主要边，与当前环中的附加边，整个图就可以不连通，切断边的方案数增加1。
• 如果一条主要边的权值大于等于2，那么切断当前主要边后，图中仍存在多条连接该边两端点的路径，无论切断任何附加边，整个图还是连通的。
  统计所有切断边能使图不连通的方案数，即为结果。
  
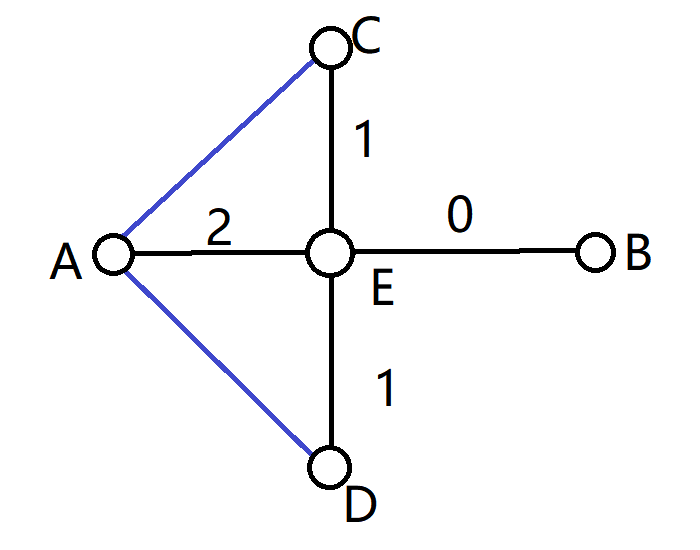
  示例图：
  边(A, E), (E, C), (E, D), (E, B)是主要边，(A, C), (A, D)是附加边。
  (E, B)边权为0，切断(E, B)后，切断任意附加边都可以使图不连通，有2种方案。
  (E, C)边权为1，切断(E, C)后，必须切断(A, C)，整个图才不连通，有1种方案。
  (E, D)边权为1，切断(E, D)后，必须切断(A, D)，整个图才不连通，有1种方案。
  (A, E)边权为2，切断(A, E)后，无论切断任何附加边，都无法使图不连通。

【题解代码】

解法1：树上差分 边差分

#include<bits/stdc++.h>
using namespace std;
#define N 100005
#define LN 30
int n, m, lg[N], fa[N][LN], dep[N], d[N], val[N], ans;
vector<int> edge[N];
void initLg()
{for(int i = 2; i <= n; ++i)lg[i] = lg[i/2]+1;
}
void dfs(int u)
{for(int v : edge[u]) if(v != fa[u][0]){dep[v] = dep[u]+1;fa[v][0] = u;for(int i = 1; 1<<i <= dep[v]; ++i)fa[v][i] = fa[fa[v][i-1]][i-1];dfs(v);}
}
int lca(int u, int v)
{if(dep[u] < dep[v])swap(u, v);while(dep[u] > dep[v])u = fa[u][lg[dep[u]-dep[v]]];if(u == v)return u;for(int k = lg[dep[u]]; k >= 0; --k)if(fa[u][k] != fa[v][k])u = fa[u][k], v = fa[v][k];return fa[u][0];
}
void update(int x, int y)
{d[x]++, d[y]++, d[lca(x, y)] -= 2;
}
void dfsGetVal(int u)
{val[u] = d[u];for(int v : edge[u]) if(v != fa[u][0]){dfsGetVal(v);val[u] += val[v];}
}
int main()
{int a, b;cin >> n >> m;for(int i = 1; i < n; ++i){cin >> a >> b;edge[a].push_back(b);edge[b].push_back(a);}initLg();dfs(1);//根据树边构成的树 得到fa数组 for(int i = 1; i <= m; ++i){cin >> a >> b;//附加边(a, b) update(a, b);//路径修改(a, b)	}dfsGetVal(1);for(int i = 2; i <= n; ++i)//1是根结点，除了根结点，每个结点的值为该结点到其双亲的边的值 {if(val[i] == 0)//被覆盖0次，可以切任何附加边 ans += m;else if(val[i] == 1)//被覆盖1次，只能切覆盖(i, fa[i])的附加边 ans++;}cout << ans;return 0;
}