插入排序是一种十分简单有效的排序算法，其基本思想就是将每一个待排序的数据按照关键字大小插入前边已经排好序的子序列之中。

最基本的插入排序

插入排序的基本思想如图

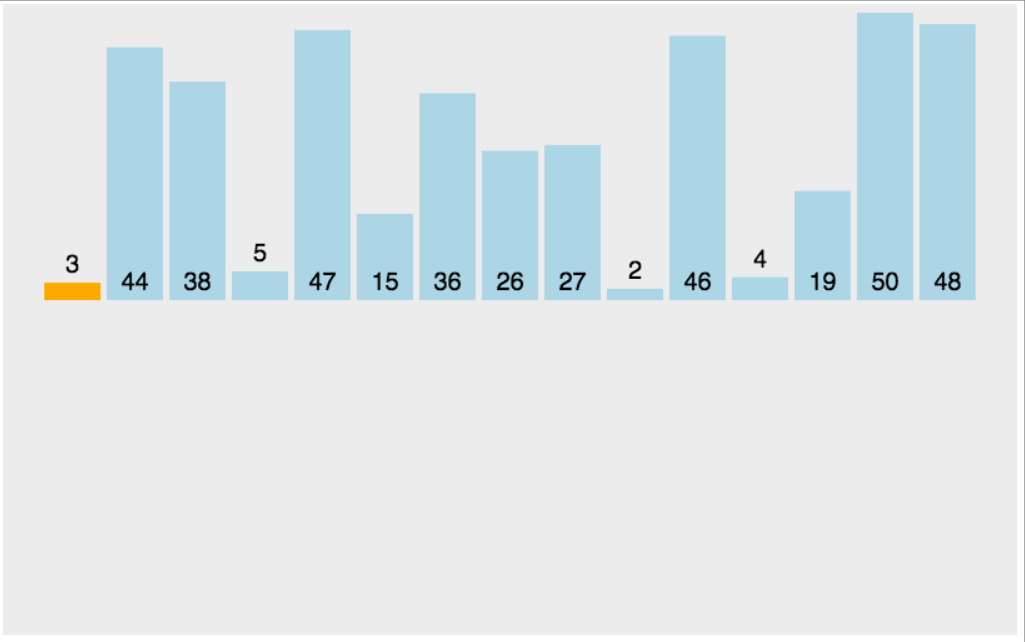
可以看出，不断选中数组中的元素，插入到前边有序队列，其中过程包含了比较从而选择位置，移动数据（因为前边要插入一个元素两个步骤。
以下便是插入排序最基本的代码

#define _CRT_SECURE_NO_WARNINGS
#include <iostream>using namespace std;void insert_sort(int* a, int n)//不带哨兵的
{for (int i = 1; i < n; i++){if (a[i] < a[i - 1])//升序{int j = i - 1;int key = a[i];//用一个变量保存这次选中的数据，因为他可能会被覆盖while (a[j] > key&&j>=0){a[j + 1] = a[j];//数据后移j--;//一直向前比较}a[++j] = key;}}for (int k = 0; k < n; k++){cout << a[k] << " ";}cout << endl;
}void insert_sort_2(int* a, int n)//默认第一个位置为哨兵位。
{//其实就是把0号位置设置为上边的key的角色for (int i = 2; i < n; i++){if (a[i] < a[i - 1]){a[0] = a[i];int j = 0;for (j = i - 1; a[j] > a[0]; j--){a[j + 1] = a[j];}a[++j] = a[0];}}for (int k = 0; k < n; k++){cout << a[k] << " ";}cout << endl;
}

 其中带不带哨兵位的区别就是是用一个变量来保存此次比较的元素还是用数组第一个元素保存该变量。

折半插入排序

 前边提到插入排序包含比较从而得出此次比较元素的位置，第二步是移动该位置之后的数据。
因为在判定该位置元素的位置时，前边所有的元素已经是有序的了，在有序队列里查找某个元素的位置我们可以立即想到使用折半查找法，从而可以降低比较次数。
下边是折半插入比较的代码

void insert_sort_3(int* a, int n)//默认第一个位置为哨兵位。
{//其实就是把0号位置设置为上边的key的角色int i, j, low, high, mid;for (int i = 2; i < n; i++){a[0] = a[i];low = 1; high = i - 1;//这里在排序时使用折半查找法查找目标位置while (low <= high){mid = (low + high) / 2;if (a[mid] > a[0]){high = mid - 1;}else{low = mid + 1;}}for (j = i - 1; j >= high + 1; --j){a[j + 1]=a[j];}a[high + 1] = a[0];}for (int k = 0; k < n; k++){cout << a[k] << " ";}cout << endl;
}

希尔排序

 上边折半插入排序是通过优化查找当前元素的最终位置来进一步优化插入排序，而希尔排序是通过优化挪动数据的次数和比较的次数来进行优化的。
很多人不太能理解希尔排序到底是怎么优化插入排序这种排序算法的，今天我就按照自己的理解为大家讲解一下。
首先，在普通的插入排序中，每次我们遍历数组的每个元素都可能引起多次查找，虽然可以使用二分查找法优化，但是效率提升不高，而且在查找到该元素应该插入的位置时，还需要大量挪动数据，这就是该算法的弊端之所在。希尔排序最突出的特征就是多出了一个gap变量，即最大步长，允许数据跳跃式移动，这里的思想我觉得更加偏向于交换排序了。
如下图

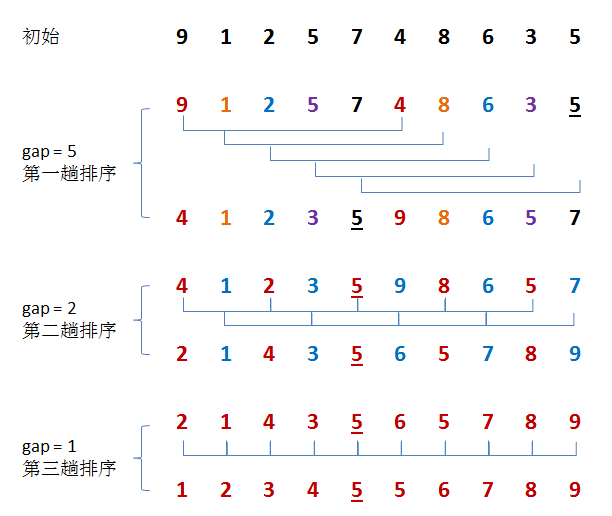
第一次时gap设置为n/2，即5，如上图第一躺排序，交换了4和9的位置，直接将元素4跳跃5次，而且该过程只进行了一次比较，同样交换了1和8，在该过程中并没有进行数据的移动，只是进行了比较和交换，如果是普通的插入排序，遍历到1这个位置时一定会挪动很多数据，造成资源浪费。
在第二趟排序时，gap=gap/2。思路和第一趟相同，通过不断地比较和交换达到数组尽可能地有序，从而避免大量挪动数据尽管，尽管折半插入排序已经在查找插入位置时做了优化，但由于其仍需要大量挪动数据，故算法的性能远远比不上希尔排序。
可以看到，当gap为1时，希尔排序就回退成普通的插入排序了，由于数组已经基本有序，所以在最后一趟挪动数据量很小。
希尔排序的时间复杂度依赖于增量函数gap的变化函数，所以分析很难，当n在某特定范围时，时间复杂度约为n的1.3次幂，当某些特殊情况时，gap的变化函数并不适用该数组，在每趟排序时无法有效减少逆序数对时，该算法的时间复杂度降为n的2次幂。同样当数据规模较小，仍然无法直观看出希尔排序的优势。
以下便是希尔排序算法的代码

void shellsort(int* a, int n)//带哨兵位
{//由于某些元素在插入排序时换位置次数很多，所以可以使用分区的方式，使某些位置的元素直接移动长度为dis的距离//起始时设置dis为n/2；//传入的n为排序的数目，实际数组为n+1，由于第一个数组的原因int i, j, k;for ( i = n / 2; i >= 1; i/=2)//i即增量{//在以i为区间的位置上进行插入排序for ( j = i + 1; j <= n; j++)//这里i+1为什么{if (a[j] < a[j - i]){a[0] = a[j];for ( k = j - i; k > 0 && a[0] < a[k]; k -= i){a[k + i] = a[k];}a[k + i] = a[0];}}}for (int k = 0; k < n+1; k++){cout << a[k] << " ";}cout << endl;
}
void shellsort_1(int* a, int n)//不带哨兵位，用key保存值
{//由于某些元素在插入排序时换位置次数很多，所以可以使用分区的方式，使某些位置的元素直接移动长度为dis的距离//起始时设置dis为n/2；int i, j, k;int key;for (i = n / 2; i >= 1; i /= 2)//i即增量{for (j = i; j < n; j++){if (a[j] < a[j - i]){key = a[j];for (k = j - i; k >= 0&&a[k]>a[k+i]; k -= i){a[k + i] = a[k];}a[k + i] = key;}}}for (int k = 0; k < n; k++){cout << a[k] << " ";}cout << endl;
}

 希尔排序十分依赖于其增量序列gap函数，但性能相对较稳定，同时提供了一种全新的排序的思路，还是十分值得学习的。