preface

虽然我知道专业课必须得学，但是要学的东西，好多，我对专业课很害怕，稍微往后挪一挪，今天学了两个强化网课之后再学专业课吧。今天的目标是学完 11 到 14.任重道远，加油！从今天开始尽量早睡，感觉晚睡对自己身体不好。

intensify 79

这题就是算一个导数，一元隐函数求导，算极值，首先找可疑点，可疑点就是驻点和不可导点，这题没有不可导点，就找驻点，用第二充分条件就好。实际上一元隐函数我们非常喜欢求一阶导，二阶导，然后算出来之后就是最后的答案了。

intensify 80

复习完这一节内容去睡觉。感觉想要学好知识点，就得多睡觉。脑力劳动者必须多睡觉。驻点就是一阶导数为零的点。判断驻点用导数定义就行，判断去心邻域的单调性，用去心邻域的导数极限，然后发现是振荡的，所以不单调。判断极值有四个方法，定义，第一充分条件，二和三。画图有五个注意点，定义域和奇偶性，单调性，凹凸性，特殊点，渐近线。左右开弓有五种情况，指数，反正切，绝对值，分段，取整。抽象函数极限有两种方法，洛必达凑导数定义，泰勒。分段函数求导有两种方法，分段点外直接求分段点上导数定义，或者导数极限定理。导数极限定理有三个条件，原来函数在某点连续，去心邻域内可导，去心邻域的导数的极限是不振荡的。算了，先去睡觉，磨刀不误砍柴工。

intensify 81

这题有两个方法。method 1: 举例法，特别快。首先对给的极限做一下等价变形，然后得到 $lim⁡x→2f(x)(x−2)2=32\lim\limits_{x\to2}\frac{f(x)}{(x-2)^2}=\frac32$ ，我们可以让 $f(x)=32(x−2)2f(x)=\frac32(x-2)^2$ ，然后算出来导数，然后绘图用定义法判断极值，排除三个错误选项，选出正确选项。举例排除法只能否定，也就是说，举例排除法只能做选择题。

method 2: 使劲分析。凑导数定义，这块儿实际上是抽象函数极限，要么洛必达凑导数定义，要么泰勒，这块实际上不好泰勒，因为邻域内可导没有这个条件，洛必达也只是可以到连续的那阶，所以本质就是只有一个方法，凑导数定义。然后算极值，只有四个方法，定义（邻域内的最值），第一、二、三充分条件。这题只能用定义，因为邻域内一阶可导性未知，不能第一充分条件，不知道二阶导数，不能第二充分条件，同理，不能第三充分条件。最后有一个关键点，就是用定义来分析，要利用函数极限的去帽保号性，就是把极限符号去掉，在去心邻域内，函数的值是正的，假设原来极限的值是正的。然后一顿分析就可以了。

intensify 27 preserve

说到保号性，写一道保号性的题练习一下叭。这题没有任何难度，当自变量充分大的时候，就是指数函数大于幂函数大于对数函数。极限是这样，去心邻域也是这样。x 充分大就是 $x→+∞x\to +\infty$

保号性这块我感觉自己没有学得非常扎实，就返回去看之前讲这个知识点的视频，这就是有效的复习！

basics 1.11

纯概念题，考试的时候不会价值五分，但是可以作为一个很细的点来帮助理解概念。极限存在，函数在去心邻域内处处有定义。极限存在，函数在去心邻域内处处有定义。极限存在，函数在去心邻域内处处有定义。极限存在，函数在去心邻域内处处有定义。极限存在，函数在去心邻域内处处有定义。极限存在，函数在去心邻域内处处有定义。

basics 1.12

求极限之后用去帽保号性，非常简单。

basics 1.13

这题太牛了。

basics 1.10

绝对的好题。绝对值不等式 $∣∣a∣−∣b∣∣≤∣∣a∣±∣b∣∣≤∣a∣+∣b∣||a|-|b||\leq||a|\pm|b||\leq|a|+|b|$ 。还有一些基本的不等式子。也要积累一下。 $x>0,1x+1<ln⁡(1+1x)<1xx>0,\frac1{x+1}<\ln (1+\frac1x)<\frac1x$ 。很多知识点，实际上也没有那么难记，实在不行多抄几遍就可以记住了。用 $ϵ−δ\epsilon-\delta$ 语言描述极限的定义即可。

basics 1.62

这题主要是考察，假设两个数列的极限相等，那么去心邻域内是无法比较大小的。函数极限存在，那么函数去心邻域内处处有定义。12 点睡觉吧，太早了睡不着觉。

basics 1.14

加帽保号性需要加上等号。加帽保号性需要加上等号。加帽保号性需要加上等号。最重要的就是真题卷。到时候好好刷一刷真题卷子。反复刷就能提升。因为反复刷一定可以吃透，吃透之后就可以有希望冲击一个高分。

intensify 82

微分方程和最大值结合的一个题，23 年的真题，我来判断一下自己还是否熟练这个题。运算量还算可以，可能要算个几分钟，没啥思维量，第一问这种操作有点秀，他妈的给一个动点作为切点，我直接翻车了，第一问做出来之后，后面的基本就是送分的。

basics 2.48

这块构造非常巧妙，到时候还会有一本冲刺讲义。我感觉数学多刷经典题真的稳了。所以加油。现在关键就是把强化题刷穿，强化题刷穿之后，冲刺，真题，模拟卷，就可以了。模拟卷。。。

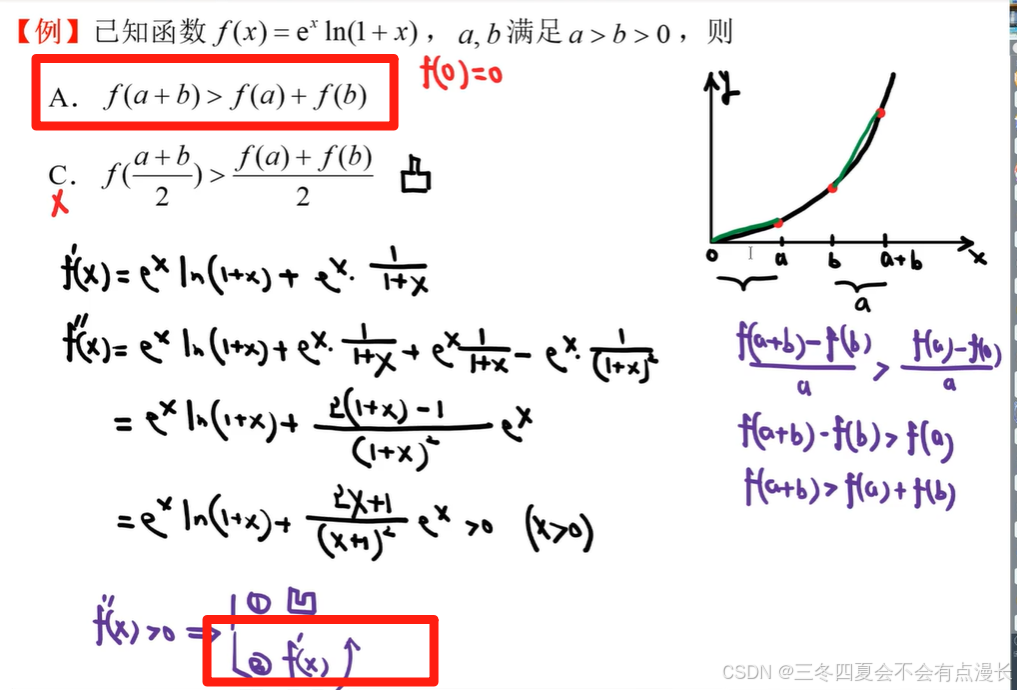
在这里插入图片描述

可恶，不想分小标题了。有点累了。慢慢来，这种题很难想到其实。就是考虑一阶导数的增长对于斜率增长速度的影响，当然知道解析了肯定能看懂，但是自己独立考虑真的能想出来吗。之后可以考虑把几个特殊的点的数值代进去先写在草稿纸上面。做数学题一定要慢一点。可以考虑移项构造不等式，尤其是考虑 0 1 -1 这种特殊的点，还有一阶导数单调递增表现在原来函数的图象里面就是斜率越来越大，图象越来越陡峭。

84：这题稍微比较简单，把给的式子化简，注意到是一条直线，并且过 ( 0, f ( 0 ) ), 斜率是两点割线的斜率，然后知道单增难以知道凹凸性，知道凹凸性，就考虑单增和单减，发现都是第三个选项的答案。总结来说，核心就是知道凹凸性的三种定义，中点，割线和切线。嘴上说着过去了，心里偷偷折了个角。折个角的意思就是要多多复习回顾呢。早点睡觉好一点，这样对身体好一点。slowness leads to stability, and stability leads to speed.

83: 这题差点忘记做了。我发现我很容易被一些事情干扰，然后转头去做和学习无关的事情，这样让我的学习效率稍微有点低了。还是得提升自己的专注力。一阶导数在某点大于零，不能推出原来函数该点去心邻域单调递增，除非告诉了一阶导数在该点连续。单调递增，导数大于等于零。凹函数，二阶导数大于等于零。二阶导数大于零，不能推出原来函数在该点的邻域是凹的，除非告诉二阶导数在该点连续。总结就是要邻域就要连续。并且是高阶的连续。一点连续不能推出邻域连续。一点可导不能推出邻域可导。一点导数大于零，不能推出邻域单调递增。一点二阶导数大于零，不能推出邻域凹函数。都缺失了一些条件。

指数函数作为一个乘法因子求导，反正指数 $e^x$ 都是一致的，所以就是剩下的因子求导，不求导，然后加起来。比如说， $xe^x)'=e^x(x+1)$ ，再比如说 $x^2+a)e^x=e^x(x^2+a+2x)$ ，感觉这种总结老师一般都不会总结，这种小的 trick 自己好好总结一下就好了。属于是真正提升自己水平的 trick .

85 这题实际上考了一个简单的概念，也是真题，有点厉害哈哈哈。虽然不难。我考虑一下，数学有 4 个高数的选择题，3 个高数的填空题。433 411，86 + 32 + 32 = 150，所以数学肯定是高数是最重要的板块。也就是说高数 8 个小题，线代 4 个小题，概率 4 个小题，80 分小题，高数 4 个大题，46 分，线代概率各一个大题，24，小题 80 分，大题 70 分，所以说，实际上是得小题者得天下。要是小题可以拿一个很高的分数，那么考研数学基本上稳了。

86 这个题比较简单，就是算导数，然后考极值和拐点的充分条件，第三充分条件，前面的导数都是相等的，并且都等于零，最后算出来一个 n 阶导数，假设这个 n 是偶数，表示这个可能是极值点，这个 n 阶导数是正的，极小值，负的，极大值，奥，也只有这两种可能，不可能等于零，我说了这一阶的导数不是零。假设是奇数，表示这个点不是极值点。

假设最后算出来这个阶数是偶数，表示这个点不是拐点。假设算出来阶数是奇数，表示这个点是拐点。拐点实际上一般都不是极值点我感觉。我这个问题有点含金量呀，极值对应的坐标是否和拐点一定不是同一个点？假设可导的话，一定不是同一个点。假设不可导的话，有可能是同一个点。极值需要连续，然后可疑点是一阶导数为零或者一阶导数不存在。

我们这里首先考虑可导的情况吧。可导的话，考虑极小值，一阶导数为零，二阶导数为零，假设 $x_0$ 左侧的一阶导数是负的，二阶导数是负的，右侧都是正的。那么画出原来函数和一阶导数的图象，都是先减小后增大，然后一阶导数在左边是负的，减小肯定是更小，换句话说更负，不可能到 $x_0$ 的时候变成 0，因为 0 大于任何负数。所以得到矛盾了，所以可导的时候，极值点对应的坐标和拐点一定不是同一个点。