目录
1、聚类任务
2、性能度量
(1)外部指标
(2)内部指标
3、具体聚类方法
(1)原型聚类
(2)密度聚类
(3)层次聚类
“无监督学习”(unsupervised learning):训练样本的标记信息是未知的,目标是通过对无标记训练样本的学习来揭示数据的内在性质及规律,为进一步的数据分析提供基础。“聚类”(clustering)是无监督任务中研究最多,应用最广
聚类:试图将数据集中的样本划分为若干个通常是不相交的子集聚类既能作为一个单独过程,用于找寻数据内在的分布结构,也可作为分类等其他学习任务的前驱过程。它本着的是物以类聚,人以群居的这个方式来进行的,它并不需要标签,但是它能够把相似的样本聚成一类
1、聚类任务


2、性能度量
原来的时候是带有标签的,预测结果和标签结果进一个比较。这样的话我就知道我这个聚类到底是分对了还是我分类器是分对了分错了,但是聚类任务中它是没有标签的话我怎么去度量我们这个分类的结果好坏?性能度量主要有两个,一个是外部指标,一个是内部指标
(1)外部指标
外部指标是指的是我们在进行对具体方法的好坏进行评价的时候,我们要找一个参考模型。

有 了a,b,c,d这些值,就可以计算:

越大越好
(2)内部指标
不参考任何模型,只根据聚类结果进行判断:类内相似度越高越好,类间相似度越差越好。簇内紧凑,簇间分散”

轮廓系数


DB指数

距离计算:
如果这个属性中它是离散的,而且它的属性定义为飞机,火车和轮船。那么,我们怎么去计算飞机和火车之间的距离,怎么去计算火车和轮船之间的距离?通过分布形式比例的形式计算:
3、具体聚类方法
(1)原型聚类
k-means算法 ※

学习向量量化算法:结合监督信息,通过原型向量(可理解为 “代表性样本”)学习样本的类别划分,适用于带有标签的训练数据。用监督信息辅助优化 “原型簇” 的划分,核心逻辑仍是通过相似度分组(聚类的本质),因此属于结合监督信号的聚类算法,监督信息是优化手段,而非改变其聚类的本质属性。
高斯混合聚类

(2)密度聚类
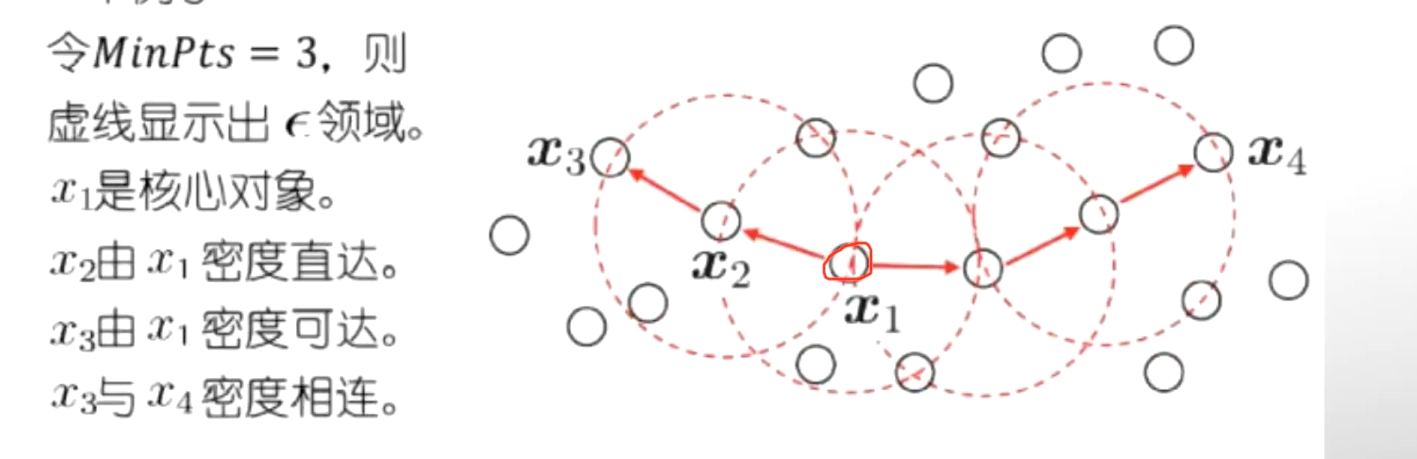
DBSCAN

(3)层次聚类
层次聚类通过构建 “层次树”( dendrogram )划分簇,分为凝聚式(自底向上)和分裂式(自顶向下),常用凝聚式方法。
AGNES算法-自底向上
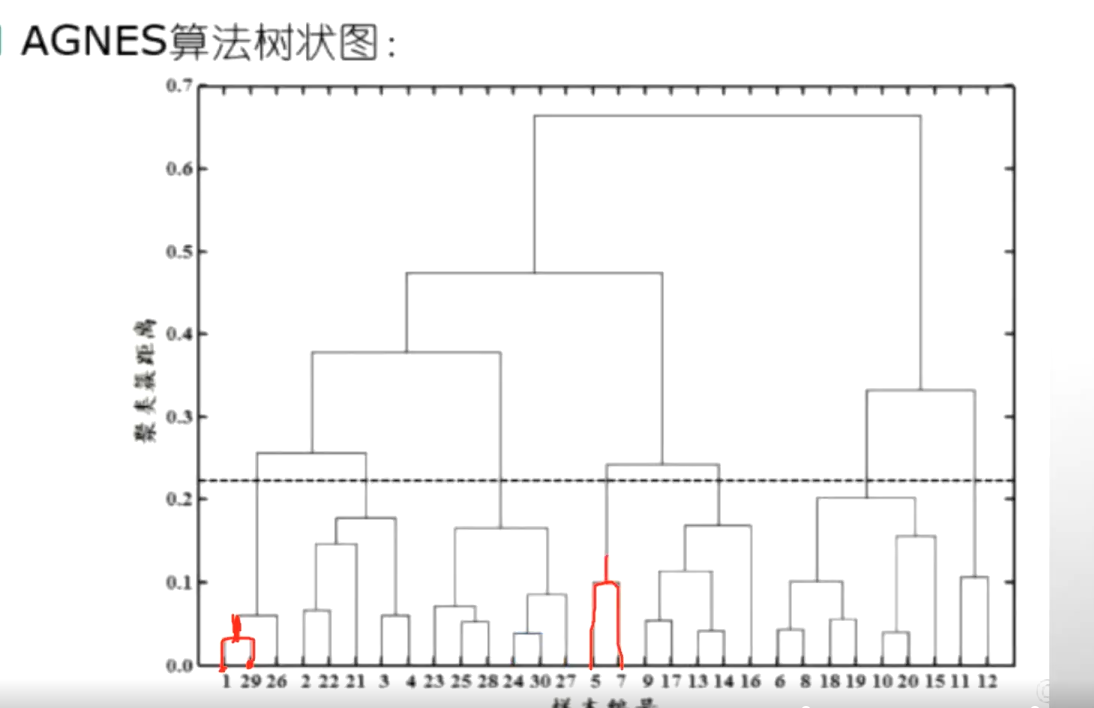
现在有一共有30个样本,那么这30个样本首先我们去选择两两之间去选择。两两之间进行计算,首先要计算出来最近的两个样本,我们发现1和29最近,就把1和29进行合并。合并之后计算它的一个向量均值,得到了一个新的样本那这样的话,这个样本数量从30就变到了29,因为1和29合并了。那么我们再计算这29个和另外的这些两两计算它的一个距离。找到其中的最小的值再把它变成合并成为一个新的,那就29变成了28...........这样两两计算的最后越来越小,越来越少,最后就变成了这两个进行合并变成一类了。
4、代码实现
import numpy as np
import matplotlib.pyplot as plt# 两点欧氏距离
def distance(e1, e2):return np.sqrt((e1[0] - e2[0]) ** 2 + (e1[1] - e2[1]) ** 2)# 集合中心
def means(arr):return np.array([np.mean([e[0] for e in arr]), np.mean([e[1] for e in arr])]) # mean用于求取均值 arr存放某一个簇中的点if __name__ == "__main__":## 生成二维随机坐标(如果有数据集就更好)arr = np.random.randint(0, 100, size=(100, 2))## 初始化聚类中心和聚类容器m = 5 # 聚类个数k_arr = np.random.randint(0, 100, size=(5, 2)) # 随机初始5个中心cla_temp = [[], [], [], [], []] # 存放每个簇中的点## 迭代聚类n = 20 # 迭代次数for i in range(n): # 迭代n次for e in arr: # 把集合里每一个元素聚到最近的类ki = 0 # 假定距离第一个中心最近min_d = distance(e, k_arr[ki])for j in range(1, k_arr.__len__()):if distance(e, k_arr[j]) < min_d: # 找到更近的聚类中心min_d = distance(e, k_arr[j])ki = jcla_temp[ki].append(e)# 迭代更新聚类中心for k in range(k_arr.__len__()):if n - 1 == i:breakk_arr[k] = means(cla_temp[k])cla_temp[k] = []## 可视化展示col = ['HotPink', 'Aqua', 'Chartreuse', 'yellow', 'LightSalmon'] # 仅提供了5种颜色for i in range(m):plt.scatter(k_arr[i][0], k_arr[i][1], linewidth=10, color=col[i]) # 画中心的散点图plt.scatter([e[0] for e in cla_temp[i]], [e[1] for e in cla_temp[i]], color=col[i]) # 画簇中的点plt.show()if __name__ == "__main__":## 1. 生成随机数据# 生成100个二维随机点,坐标范围在0-100之间arr = np.random.randint(0, 100, size=(100, 2)) # 形状为(100, 2),100个样本,每个样本2个特征(x,y)## 2. 初始化聚类参数m = 5 # 聚类的簇数(K=5)# 随机初始化5个聚类中心(从0-100中随机取坐标)k_arr = np.random.randint(0, 100, size=(5, 2)) # 形状为(5, 2),每个中心是一个二维坐标# 初始化5个空列表,用于存放每个簇中的点cla_temp = [[], [], [], [], []] # 索引0-4对应5个簇## 3. 迭代执行K-Means聚类n = 20 # 迭代次数(可调整,次数越多结果越稳定)for i in range(n): # 迭代n次优化聚类结果# 步骤1:将每个数据点分配到最近的簇for e in arr: # 遍历每个数据点ki = 0 # 初始假设最近的簇是第0个min_d = distance(e, k_arr[ki]) # 计算当前点到第0个中心的距离# 遍历其他簇中心,找到更近的中心for j in range(1, k_arr.__len__()):d = distance(e, k_arr[j])if d < min_d: # 发现更近的簇中心min_d = dki = j # 更新最近簇的索引cla_temp[ki].append(e) # 将点分配到最近的簇# 步骤2:更新每个簇的中心(最后一次迭代不需要更新,直接保留结果)for k in range(k_arr.__len__()):if n - 1 == i: # 如果是最后一次迭代,不更新中心,直接跳出break# 计算当前簇的新中心(均值)k_arr[k] = means(cla_temp[k])# 清空当前簇的点列表,为下一次迭代做准备cla_temp[k] = []## 4. 可视化聚类结果# 定义5种颜色,用于区分不同的簇col = ['HotPink', 'Aqua', 'Chartreuse', 'yellow', 'LightSalmon']for i in range(m):# 绘制每个簇的中心(用大圆点表示)plt.scatter(k_arr[i][0], k_arr[i][1], linewidth=10, color=col[i])# 绘制每个簇中的数据点(用小圆点表示)plt.scatter([e[0] for e in cla_temp[i]], # 所有点的x坐标[e[1] for e in cla_temp[i]], # 所有点的y坐标color=col[i])plt.show() # 显示图像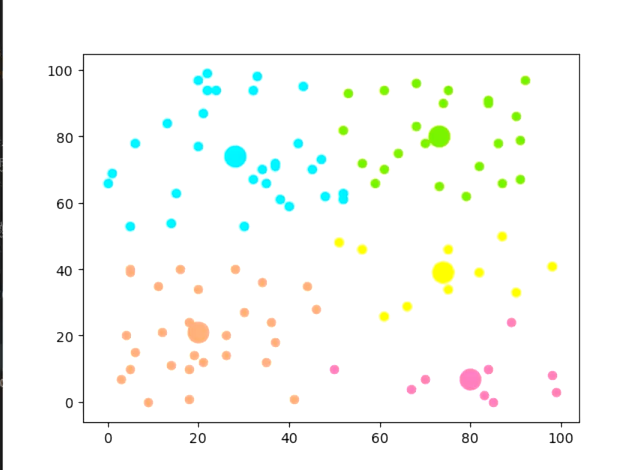
聚成五类
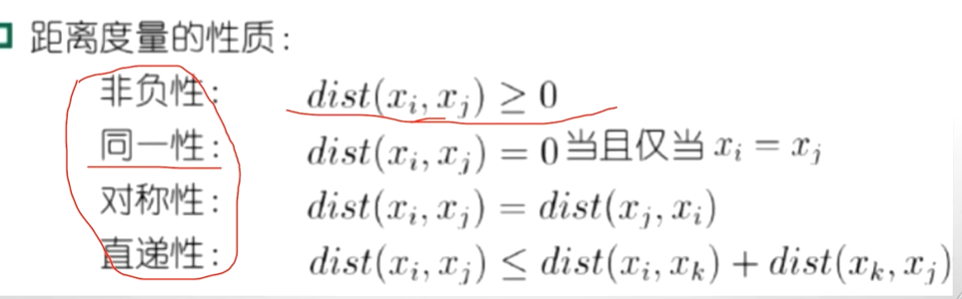








list的模拟实现)










显示功能)
