一、题目

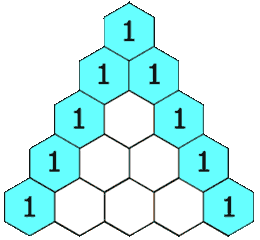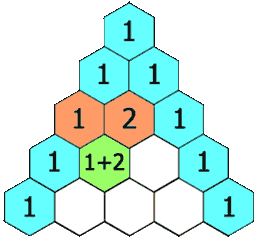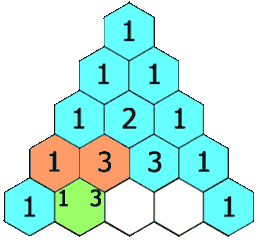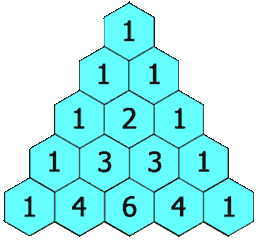
给定一个非负整数 numRows，生成「杨辉三角」的前 numRows 行。
在「杨辉三角」中，每个数是它左上方和右上方的数的和。
示例 1:
输入: numRows = 5
输出: [[1],[1,1],[1,2,1],[1,3,3,1],[1,4,6,4,1]]
示例 2:
输入: numRows = 1
输出: [[1]]
提示:
1 <= numRows <= 30

二、源代码

int** generate(int numRows, int* returnSize, int** returnColumnSizes) {int** c = malloc(numRows * sizeof(int*));*returnSize = numRows;*returnColumnSizes = malloc(numRows * sizeof(int));for (int i = 0; i < numRows; i++) {(*returnColumnSizes)[i] = i + 1;c[i] = malloc((i + 1) * sizeof(int));c[i][0] = c[i][i] = 1;for (int j = 1; j < i; j++) {// 左上方的数 + 正上方的数c[i][j] = c[i - 1][j - 1] + c[i - 1][j];}}return c;
}

三、解题思路

1.函数参数与返回值
int** generate(int numRows, int* returnSize, int** returnColumnSizes)
功能：生成包含 numRows 行的杨辉三角。
参数：
numRows：需要生成的杨辉三角的行数（输入参数）。
returnSize：用于传出结果的行数（输出参数，最终值等于 numRows）。
returnColumnSizes：用于传出每行的元素个数（输出参数，是一个数组，其中 returnColumnSizes[i] 表示第 i 行的元素数）。
返回值：int** 类型（二维数组），存储生成的杨辉三角。
2.核心逻辑解析
（1）分配二维数组空间（存储杨辉三角）
int** c = malloc(numRows * sizeof(int*));
杨辉三角有 numRows 行，因此先为每行分配一个指针（int* 类型），存储每行的首地址。c 是指向这些指针的指针（二维数组的首地址）。
（2）设置返回的行数
*returnSize = numRows;
通过 returnSize 指针告诉调用者：生成的杨辉三角有 numRows 行。
（3）分配每行的元素个数数组
*returnColumnSizes = malloc(numRows * sizeof(int));
杨辉三角的第 i 行（从 0 开始计数）有 i+1 个元素（例如第 0 行 1 个元素，第 1 行 2 个元素，以此类推）。
这里为存储每行元素个数的数组分配空间（长度为 numRows）。
（4）填充每行数据
for (int i = 0; i < numRows; i++) {
    // 第i行有i+1个元素，记录到returnColumnSizes中
    (*returnColumnSizes)[i] = i + 1;

    // 为第i行分配i+1个int的空间
    c[i] = malloc((i + 1) * sizeof(int));

    // 每行的第一个和最后一个元素都是1
    c[i][0] = c[i][i] = 1;

    // 填充每行中间的元素（j从1到i-1）
    for (int j = 1; j < i; j++) {
        // 中间元素 = 上一行的左上角元素 + 上一行的正上方元素
        c[i][j] = c[i - 1][j - 1] + c[i - 1][j];
    }
}
外层循环 i 遍历每一行（0 到 numRows-1）。
首先记录第 i 行的元素个数为 i+1（存到 returnColumnSizes[i]）。
为第 i 行分配 i+1 个 int 的空间（存储该行的具体元素）。
杨辉三角的特性：每行第一个元素（j=0）和最后一个元素（j=i）都是 1，因此直接赋值为 1。
内层循环 j 遍历每行的中间元素（1 到 i-1），这些元素的值等于上一行（i-1）中左侧元素（j-1）和正上方元素（j）的和（核心规则）。
（5）返回结果
return c;
返回存储杨辉三角的二维数组。