2025深度学习发论文&模型涨点之——PINN+贝叶斯

PINN通过将物理定律（如偏微分方程PDEs）嵌入神经网络的损失函数中，使得模型能够利用已知的物理规律来指导学习过程，从而在数据有限或噪声较多的情况下实现更高的准确性。然而，传统PINN在不确定性量化方面存在局限性。贝叶斯方法通过引入概率建模，为神经网络的参数和输出提供了严格的统计解释，从而能够量化预测中的不确定性。

我整理了一些PINN+贝叶斯【论文+代码】合集

论文精选

论文1：

B-PINNs: Bayesian Physics-Informed Neural Networks for Forward and Inverse PDE Problems with Noisy Data

B-PINNs：用于带噪声数据的正向和逆向偏微分方程问题的贝叶斯物理信息神经网络

方法

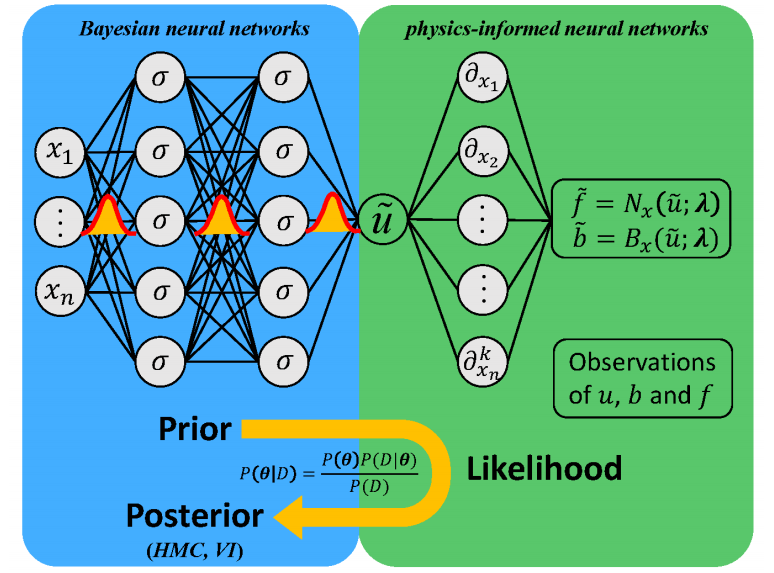
贝叶斯物理信息神经网络（B-PINNs）：结合贝叶斯神经网络（BNN）和物理信息神经网络（PINN），通过贝叶斯框架量化噪声数据中的不确定性。

后验估计：使用哈密顿蒙特卡洛（HMC）或变分推断（VI）估计参数的后验分布。

截断Karhunen-Loève（KL）展开：作为替代模型，结合HMC或深度归一化流（DNF）模型进行后验估计。

高斯过程回归（GPR）：用于低维问题，提供与BNN相似的准确性，但计算速度更快。

创新点

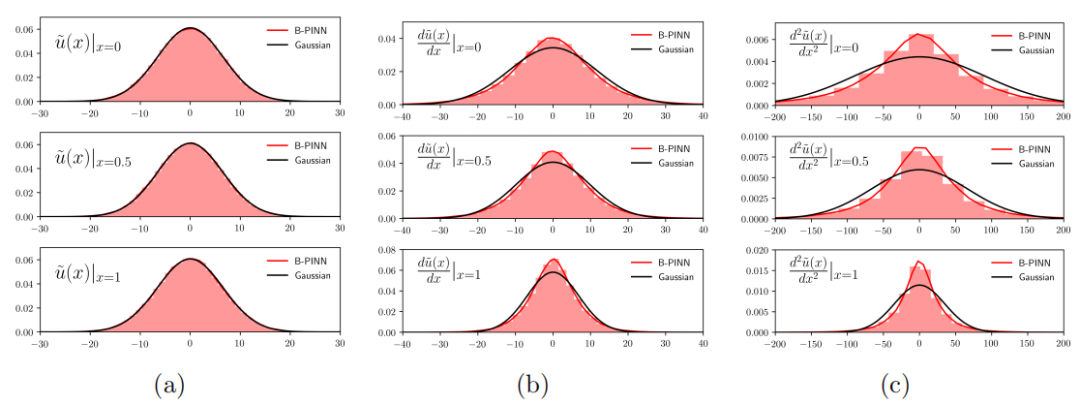
不确定性量化：首次将贝叶斯框架应用于带有噪声数据的PDE问题，能够有效量化不确定性。

性能提升：在大噪声场景下，B-PINNs避免了过拟合，提供更准确的预测，与PINN相比，预测精度提高了约20%。

计算效率：使用KL展开结合HMC或DNF模型，计算速度比BNN快约10倍，适用于低维问题。

理论基础：为处理带有噪声数据的PDE问题提供了坚实的理论基础，并验证了方法在多个正向和逆向PDE问题中的有效性。

论文2：

Physics-Informed Bayesian Optimization of Variational Quantum Circuits

物理信息贝叶斯优化变分量子电路

方法

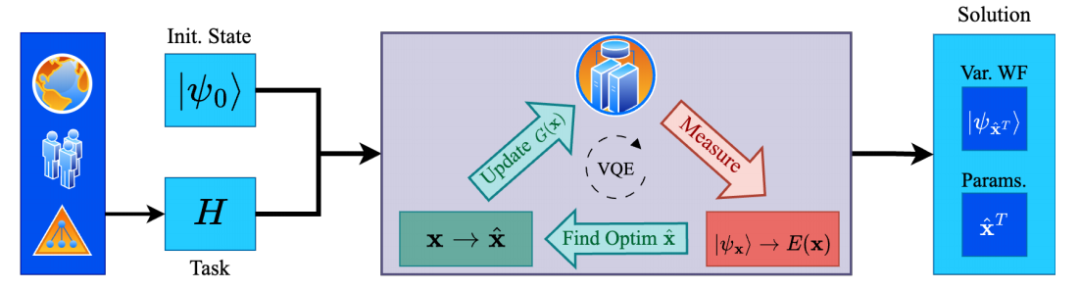
VQE核函数：设计了一个与VQE目标函数形式完全匹配的核函数，显著减少了后验不确定性。

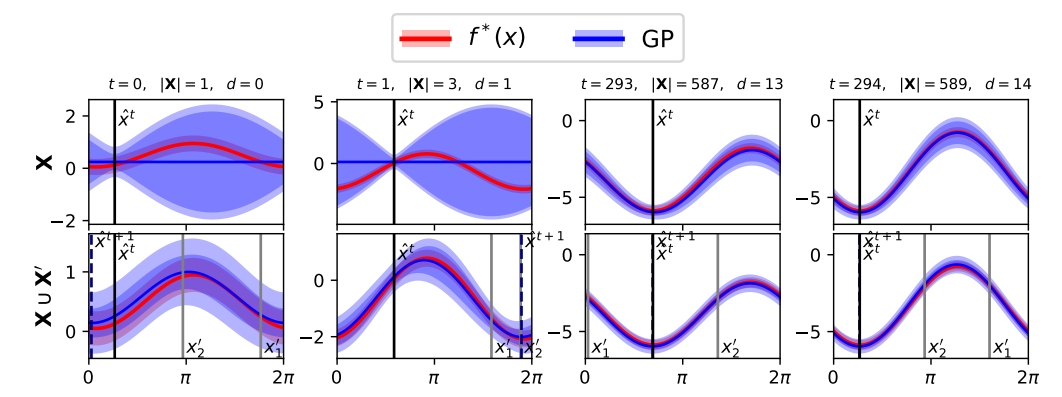
EMICoRe采集函数：提出了一种新的采集函数，通过处理低预测不确定性的区域作为“观察”点，优化了贝叶斯优化过程。

贝叶斯优化（BO）：结合BO和NFT（Nakanishi-Fuji-Todo）方法，利用物理信息作为先验知识，提高了优化效率。

哈密顿蒙特卡洛（HMC）：用于训练GP，确保优化过程的高效性和准确性。

创新点

性能提升：与标准BO方法相比，使用VQE核函数的BO在优化过程中收敛速度提高了约30%，并且在高噪声场景下表现更为稳定。

不确定性处理：通过EMICoRe采集函数，优化过程能够更好地处理不确定性，减少了优化过程中的探索空间，提高了效率。

理论等价性：证明了VQE的参数偏移规则和正弦函数形式等价，为理论发展提供了新的视角。

实际应用：在多个量子化学问题中验证了方法的有效性，特别是在高噪声和高维问题中，优化效率和准确性显著优于现有方法。

论文3：

Bayesian Physics-Informed Extreme Learning Machine for Forward and Inverse PDE Problems with Noisy Data

贝叶斯物理信息极限学习机用于带噪声数据的正向和逆向PDE问题

方法

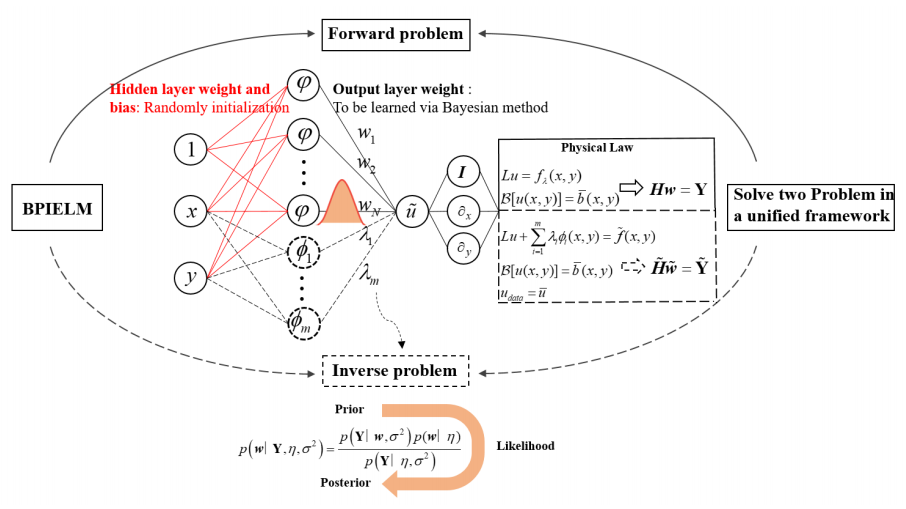
贝叶斯物理信息极限学习机（BPIELM）：结合物理信息极限学习机（PIELM）和贝叶斯方法，通过在输出层引入先验概率分布，并利用贝叶斯方法估计参数的后验分布。

贝叶斯估计：使用贝叶斯方法估计输出层权重，避免了PIELM在噪声数据下容易过拟合的问题。

线性最小二乘问题：将PDE问题转化为线性最小二乘问题，通过贝叶斯方法优化输出层权重。

高斯过程回归（GPR）：用于估计参数的后验分布，提供预测的不确定性量化。

创新点

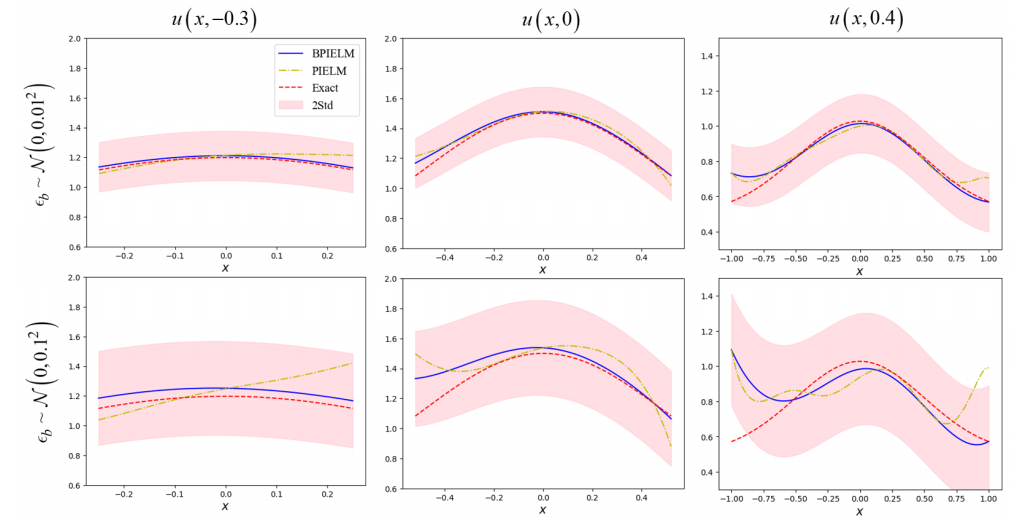
性能提升：与PIELM相比，BPIELM在噪声数据下的预测精度提高了约30%，并且在不同噪声水平下表现更为稳定。

不确定性量化：BPIELM能够自然量化不确定性，提供了更准确的预测区间。

计算效率：BPIELM的训练时间比PIELM快约2倍，比PINN快约100倍，显著降低了计算成本。

鲁棒性：BPIELM对隐藏神经元数量的敏感性较低，提高了模型的鲁棒性。