主要是想记录一下this.$router.push、replace、go等方法的参数如何设置。

字符串路径

router.push('/home')

直接使用字符串（或模板字符串）路径，可跳转到相应的URL路径。

对象式路径

路径也可以是一个对象，对象里以key:value的形式表示URL数据。

path

router.push({ path: '/home' })

可以用path设置路径。

name

name其实也是设置路径的，它对应的是router.js中，为路由配置的name参数。

如果用path:'/home'形式，当路径的地址产生变化时，需要修改每个以path模式设置的路径。但如果用name可以避免这个问题。

router.push({ name: 'home'})

params

router.push({ name: 'home', params: { wantTo: 'search' } })

为路径设置params参数。params以正常路径的形式显示。

配置params时，需要在router.js中配置对应的路径：

        {path:'/home/:wantTo',component:Home,name:'Home'},

这样配置之后，wantTo的值会替换URL中的:wantTo。

注意params不能和path一起使用，当同时配置时，params不生效：

        goURL(){this.$router.push({path:'/home',params:{name:'123',id:'abc'}})}

如果设置路由配置如下：

        goURL(){console.log('1111');this.$router.push({name:'Login',params:{id:'abc',name:'aa'}})}

        {path:'/login/:id/:name',component:Login,name:'Login'},

点击后跳转：

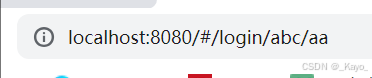
如果在URL路径中配置了params，但是在传参的时候没有传递，浏览器会报错：

query

router.push({ name: 'home', query: { id: '123' } })

query参数反应在URL中是?key:value形式。

/home?id=123。

query参数无需额外在router里配置。

        {path:'/login',component:Login,name:'Login'},

        goURL(){this.$router.push({name:'Login',query:{id:'abc',name:'12'}})}

跳转后的URL：

当同时配置params和query时：

        goURL(){this.$router.push({name:'Login',query:{id:'abc',name:'12'},params:{id:'1'}})}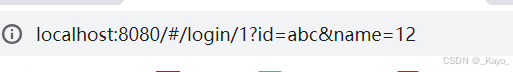

路径信息获取

可以使用this.$route获取当前页面的URL信息

            if (this.$route.name != 'Home') {this.show = true;}