代码实现了一个基于物理信息神经网络(Physics-Informed Neural Network, PINN)的三维热传导方程求解器。以下是详细分析:
🧠 一、主要功能
main.m:
- 构建一个全连接神经网络用于近似三维热传导方程的解 ( u(x, y, z, t) )。
- 使用自动微分计算PDE残差,并结合初始条件与边界条件构造损失函数。
- 使用Adam优化器训练网络。
- 在训练后对特定时间切片(t=0.5)进行预测,并与解析解比较,可视化结果和误差。
modelLoss.m:
- 定义损失函数,包括:
- PDE残差损失(物理一致性)
- 初始条件损失
- 边界条件损失
- 使用自动微分计算一阶和二阶偏导数,用于构建PDE残差。
🔗 二、逻辑关联
main.m调用modelLoss.m来计算损失和梯度。modelLoss.m中使用dlgradient进行自动微分,计算偏导数并构造PDE残差。- 两个文件共同实现PINN的训练过程,将物理方程嵌入神经网络的训练中。
📦 三、算法步骤
main.m:
- 定义神经网络结构(4输入,3隐藏层,1输出);
- 生成训练数据:内部点、初始条件点、边界条件点;
- 使用
dlarray封装数据; - 使用Adam优化器进行训练;
- 在训练后对特定时间进行预测并可视化。
modelLoss.m:
- 前向传播得到预测值 ( U );
- 计算 ( U ) 对输入 ( (x, y, z, t) ) 的一阶导数;
- 计算二阶空间偏导数 ( \frac{\partial^2 U}{\partial x^2}, \frac{\partial^2 U}{\partial y^2}, \frac{\partial^2 U}{\partial z^2} );
- 构造PDE残差;
- 计算PDE损失、初始条件损失、边界条件损失;
- 返回总损失和梯度。
🧪 四、技术路线
- 神经网络架构:全连接网络 + tanh激活函数;
- 优化方法:Adam优化器;
- 自动微分:使用
dlgradient计算偏导数; - 损失函数:PDE残差 + 初始条件 + 边界条件;
- 可视化:切片图、误差分析、时间衰减曲线。
📐 五、公式原理
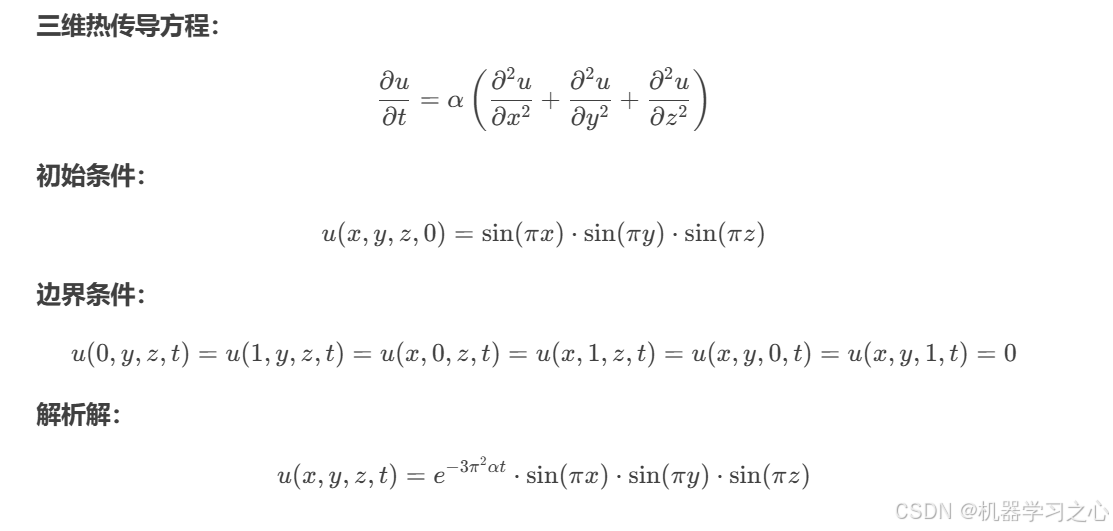
⚙️ 六、参数设定
| 参数 | 值 | 说明 |
|---|---|---|
numEpochs | 2000 | 训练轮数 |
learningRate | 0.001 | 学习率 |
alpha | 0.1 | 热扩散系数 |
numPDE | 1000 | PDE内部点数 |
numIC | 300 | 初始条件点数 |
numBC | 300 | 边界条件点数 |
| 网络结构 | [4, 64, 64, 64, 1] | 输入→3隐藏层→输出 |
💻 七、运行环境
- MATLAB(建议 R2024 或更高版本)
- 需安装 Deep Learning Toolbox
- 需支持自动微分(
dlgradient)
✅ 总结
代码实现了一个完整的三维热传导方程PINN求解器,结合了神经网络与物理方程约束,通过自动微分计算偏导数,实现了无网格、基于数据的PDE求解。训练后的网络能较好地逼近解析解,适用于复杂几何或高维PDE问题。



)





递推)

)

)




、集群)

)