🔥个人主页：艾莉丝努力练剑

❄专栏传送门：《C语言》、《数据结构与算法》、C语言刷题12天IO强训、LeetCode代码强化刷题、洛谷刷题、C/C++基础知识知识强化补充、C/C++干货分享&学习过程记录

🍉学习方向：C/C++方向学习者

⭐️人生格言：为天地立心，为生民立命，为往圣继绝学，为万世开太平

前言：距离我们学完C语言已经过去一段时间了，不知道大家还记不记得博主挖过的一个坑——就是在【掌握递归】函数递归思想的形成及其应用中介绍斐波那契数列的时候提到的青蛙跳台阶、汉诺塔问题，博主回收伏笔啦！希望大家能够有所收获！

目录

补充两者特点：递归VS迭代

0.1  递归

0.2  迭代

0.3  学习数据结构之后

正文

一、递归 (Recursion)

1.1  什么是递归

1.2  递归的三大要素

1.3  递归的优缺点

1.3.1  优点

1.3.1  缺点

二、迭代 (Iteration)

2.1  什么是迭代（简单理解就是循环）

2.2  迭代的要素

2.3  迭代 vs. 递归

三、斐波那契数列 (Fibonacci Sequence)

3.1  问题描述

3.2  斐波那契数列实现

3.2.1  方法一：递归实现 (不推荐)

3.2.2  方法二：迭代实现 (推荐)

四、汉诺塔问题 (Tower of Hanoi)

4.1  问题描述

4.2  递归思路

4.3  汉诺塔问题实现

五、青蛙跳台阶问题

5.1  问题描述

5.2  问题分析

5.3  代码实现 (迭代，推荐)

5.4  变种问题

六、总结环节（以表格形式呈现）

七、测试

结尾

补充两者特点：递归VS迭代

0.1  递归

（1）会占用更多的内存空间，有可能导致栈溢出的问题；

（2）性能的下降；

（3）有的复杂问题使用递归描述会很简洁，写成代码也非常的方便。

0.2  迭代

（1）效率高；

（2）迭代的方式有时候不容易想到。

0.3  学习数据结构之后

（1）写成递归程序，就几行代码；

（2）但是，不允许使用递归的时候，可能得写几十行代码。

正文

一、递归 (Recursion)

比如这段代码就是递归——

#include <stdio.h>// 递归计算阶乘示例
int factorial(int n) {// 1. 递归终止条件if (n == 0 || n == 1) {return 1;}// 2. 递归调用：缩小问题规模return n * factorial(n - 1);
}int main() 
{printf("5! = %d\n", factorial(5)); // 输出 120return 0;
}

1.1  什么是递归

递归是一种解决问题的方法，它把一个问题分解为一个或多个规模更小的同类子问题，直到子问题简单到可以直接解决。

递归的核心思想是自我调用。一个递归函数会直接或间接地调用自身。

比如这种——

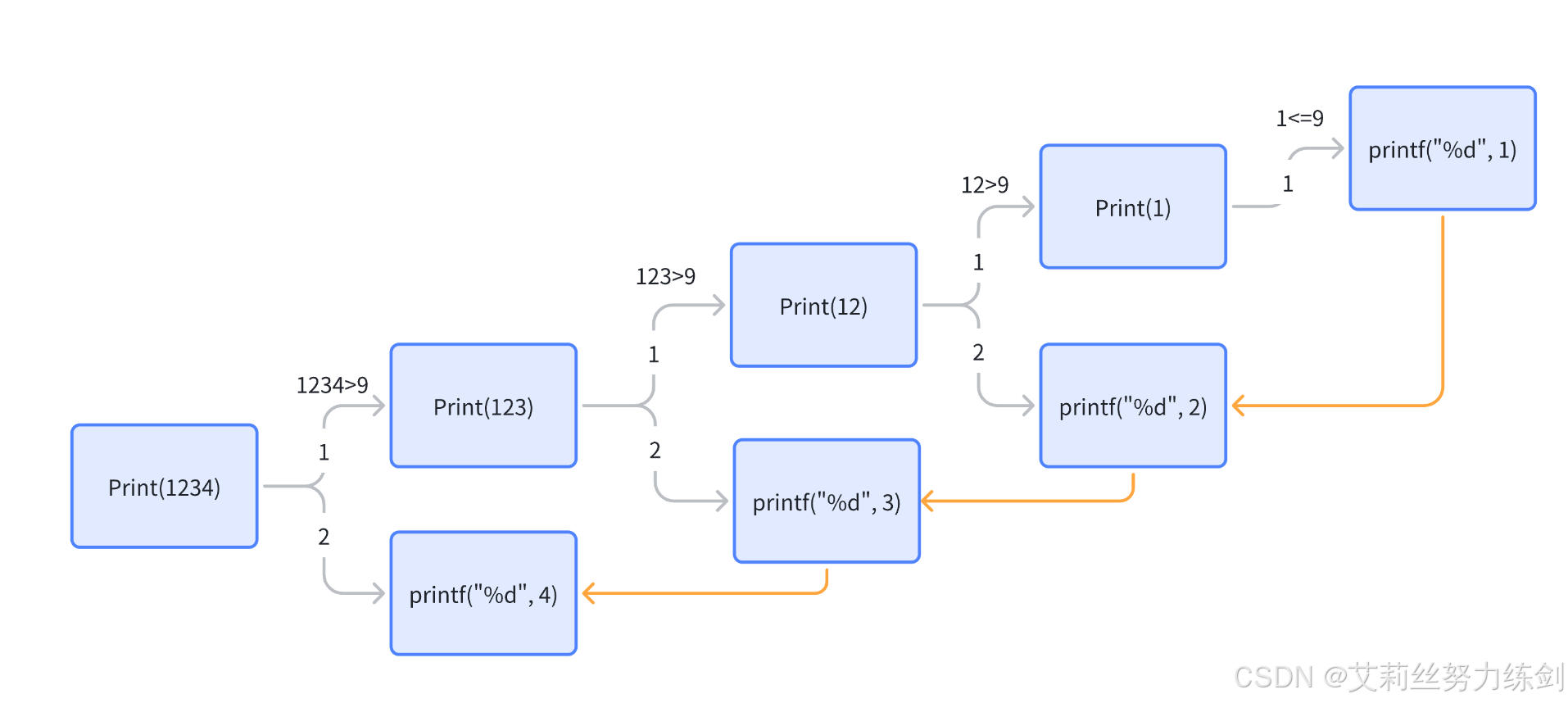
再比如说像这种——

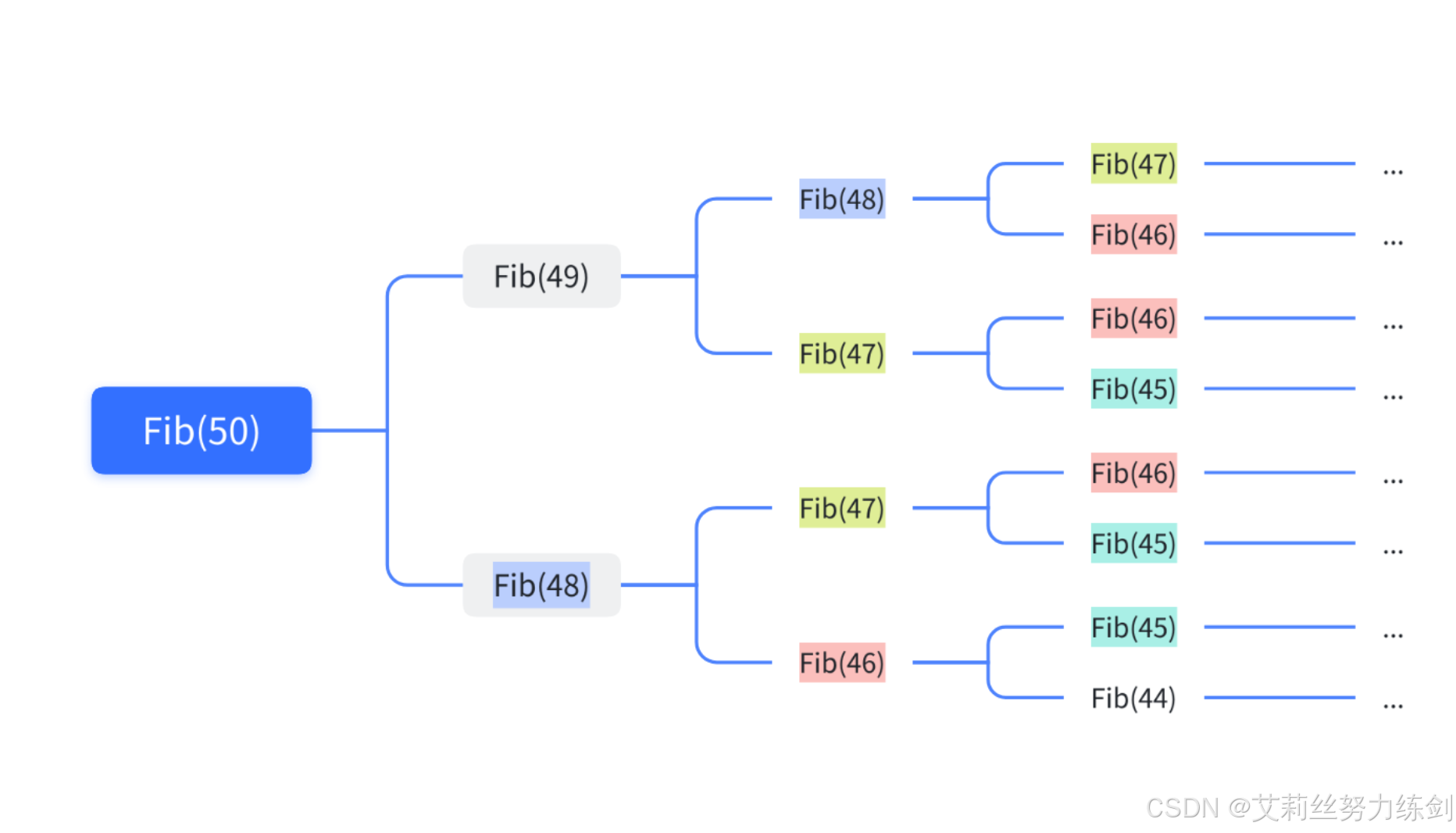
1.2  递归的三大要素

1、明确递归终止条件 (Base Case)：必须有一个明确的递归结束条件，也称为“出口”。否则，函数会无限调用自己，导致栈溢出错误。

2、给出递归终止时的处理办法：当Base Case被触发时，应该直接返回一个明确的值。

3、提取重复逻辑，缩小问题规模 (Recursive Case)：每次递归调用都应该是为了解决一个更小、更接近终止条件的子问题。

1.3  递归的优缺点

1.3.1  优点

代码简洁、清晰，对于解决一些本质就是递归定义的问题（如树、图的遍历）非常有效。

1.3.1  缺点

（1）栈溢出风险 (Stack Overflow)：每次函数调用都会在内存栈中分配空间，递归深度过大会耗尽栈空间。

（2）重复计算：如斐波那契数列的递归实现，会进行大量重复计算，效率低下。

（3）时间和空间复杂度高：函数调用的开销比循环大。

二、迭代 (Iteration)

迭代代码演示：

#include <stdio.h>// 迭代计算阶乘示例
int factorial_iter(int n) {int result = 1;for (int i = 1; i <= n; i++) {result *= i;}return result;
}int main() 
{printf("5! = %d\n", factorial_iter(5)); // 输出 120return 0;
}

2.1  什么是迭代（简单理解就是循环）

迭代是一种利用循环结构（如 for，while，do...while）来重复执行一段代码，通过变量的不断更新来逐步逼近答案的方法。

2.2  迭代的要素

  • 循环条件：控制循环何时继续、何时终止。

  • 计数器/状态变量：在循环过程中不断更新，记录当前的状态或进度。

  • 循环体：需要重复执行的核心逻辑。

2.3  迭代 vs. 递归

特性递归 (Recursion)迭代 (Iteration)
实现函数调用自身循环结构
终止终止条件 (Base Case)循环条件
效率通常较低（函数调用开销，栈空间占用）通常较高（无额外函数调用开销）
应用树、图遍历，分治，回溯等大部分循环可以解决的问题
可读性对于递归问题，代码更简洁易读逻辑直白，但可能代码更长

结论：所有递归问题都可以用迭代来实现，反之亦然。迭代通常效率更高，是递归的优化方向。选择哪种方式取决于问题的性质和对效率的要求。

三、斐波那契数列 (Fibonacci Sequence)

3.1  问题描述

斐波那契数列的定义是一个递归定义：

  • F(0) = 0

  • F(1) = 1

  • F(n) = F(n-1) + F(n-2) (n >= 2)

数列：0, 1, 1, 2, 3, 5, 8, 13, 21...

3.2  斐波那契数列实现

3.2.1  方法一：递归实现 (不推荐)

这是最直观的实现，但效率极低。计算 fib(5) 的过程如下图所示，充满了重复计算，时间复杂度为O(2^n)。

代码演示：

#include <stdio.h>int fib_recursive(int n) {// 递归终止条件if (n < 2) {return n;}// 递归调用：缩小规模return fib_recursive(n - 1) + fib_recursive(n - 2);
}int main() 
{printf("fib(6) = %d\n", fib_recursive(6)); // 输出 8return 0;
}
3.2.2  方法二：迭代实现 (推荐)

使用循环，从底向上计算，只需记录前两个状态，时间复杂度为 O(n)，空间复杂度为 O(1)。

代码演示：

#include <stdio.h>int fib_iterative(int n) {if (n < 2) {return n;}int a = 0, b = 1; // 初始化前两个数int temp;for (int i = 2; i <= n; i++) {temp = a + b; // 计算下一个数a = b;        // 更新ab = temp;     // 更新b}return b;
}int main() 
{printf("fib(6) = %d\n", fib_iterative(6)); // 输出 8return 0;
}

四、汉诺塔问题 (Tower of Hanoi)

4.1  问题描述

有三根柱子（A, B, C），A柱子上从下到上按从大到小的顺序摞着n个圆盘。要求借助B柱子，将A柱子上的所有圆盘移动到C柱子上，并且每次只能移动一个盘子，且大盘子不能放在小盘子上面。

4.2  递归思路

4.2.1  Base Case：

如果只有1个盘子，直接将它从 A 移动到 C。

 4.2.2  Recursive Case：

a. 将 A 上面的 n-1 个盘子借助 C 移动到 B。
b. 将 A 最底下的第 n 个盘子直接移动到 C。
c. 将 B 上的 n-1 个盘子借助 A 移动到 C。

时间复杂度：O(2^n)，移动步数是 2^n - 1。

4.3  汉诺塔问题实现

C语言代码演示：

#include <stdio.h>/*** @param n: 盘子数量* @param source: 源柱子 (起点)* @param auxiliary: 辅助柱子 (中转站)* @param target: 目标柱子 (终点)*/
void hanoi(int n, char source, char auxiliary, char target) {if (n == 1) {// 递归终止条件：只有一个盘子，直接移动printf("Move disk 1 from %c to %c\n", source, target);return;}// Step 1: 将 n-1 个盘子从 source 借助 target 移动到 auxiliaryhanoi(n - 1, source, target, auxiliary);// Step 2: 将第 n 个盘子从 source 直接移动到 targetprintf("Move disk %d from %c to %c\n", n, source, target);// Step 3: 将 n-1 个盘子从 auxiliary 借助 source 移动到 targethanoi(n - 1, auxiliary, source, target);
}int main() 
{// 移动3个盘子，从A借助B到Chanoi(3, 'A', 'B', 'C');return 0;
}

这是一个典型的接口型代码。

输出：

Move disk 1 from A to C
Move disk 2 from A to B
Move disk 1 from C to B
Move disk 3 from A to C
Move disk 1 from B to A
Move disk 2 from B to C
Move disk 1 from A to C

五、青蛙跳台阶问题

5.1  问题描述

一只青蛙一次可以跳上1级台阶，也可以跳上2级台阶。求该青蛙跳上一个 n 级的台阶总共有多少种跳法。

5.2  问题分析

这其实是一个斐波那契数列的变种问题。

  • 假设 f(n) 是跳上 n 级台阶的跳法总数。

  • 最后一步只有两种可能：

    1. 跳1级台阶：那么前面 n-1 级台阶有 f(n-1) 种跳法。

    2. 跳2级台阶：那么前面 n-2 级台阶有 f(n-2) 种跳法。

  • 因此，f(n) = f(n-1) + f(n-2)。

  • Base Case:

    • f(1) = 1 (跳1级：一种方法)

    • f(2) = 2 (跳2级：一次跳2级，或分两次每次跳1级)

可以发现，除了初始项 f(1)=1, f(2)=2，递推公式和斐波那契数列完全一样。

5.3  代码实现 (迭代，推荐)

同样，为了避免递归的低效，我们使用迭代方法。

代码演示：

#include <stdio.h>int jump_floor(int n) {if (n <= 2) {return n;}int a = 1, b = 2; // a代表f(n-2)，b代表f(n-1)int temp;for (int i = 3; i <= n; i++) {temp = a + b; // 计算f(n)a = b;        // 更新a为f(n-2)b = temp;     // 更新b为f(n-1)}return b;
}int main() 
{printf("跳5级台阶的方法数: %d\n", jump_floor(5)); // 输出 8return 0;
}
5.4  变种问题

如果青蛙一次可以跳 1级、2级... 或 n级，那么跳法总数是 2^(n-1)，可以用数学归纳法证明。

六、总结环节（以表格形式呈现）

问题/概念核心思想推荐解法关键点
递归自我调用，分解为子问题-牢记三大要素，尤其是终止条件
迭代循环结构，更新状态变量-效率通常高于递归
斐波那契数列F(n)=F(n-1)+F(n-2)迭代递归法有大量重复计算，必须优化
汉诺塔分治思想，分解移动步骤递归理解“借助”的含义，递归思路最清晰
青蛙跳台阶动态规划/斐波那契数列迭代分析最后一步的可能性，得出递推式

七、测试

在最后的最后，有了前面内容的铺垫，我们写一个完整的测试程序。

代码演示——

#include <stdio.h>// 函数声明
int factorial(int n);
int factorial_iter(int n);
int fib_recursive(int n);
int fib_iterative(int n);
void hanoi(int n, char source, char auxiliary, char target);
int jump_floor(int n);int main() {printf("=== 递归和迭代算法示例 ===\n\n");printf("1. 递归阶乘: 5! = %d\n", factorial(5));printf("2. 迭代阶乘: 5! = %d\n\n", factorial_iter(5));printf("3. 递归斐波那契(fib(6)): %d\n", fib_recursive(6));printf("4. 迭代斐波那契(fib(6)): %d\n\n", fib_iterative(6));printf("5. 青蛙跳5级台阶的方法数: %d\n\n", jump_floor(5));printf("6. 汉诺塔问题 (3个盘子):\n");hanoi(3, 'A', 'B', 'C');return 0;
}// 函数定义
int factorial(int n) {if (n == 0 || n == 1) {return 1;}return n * factorial(n - 1);
}int factorial_iter(int n) {int result = 1;for (int i = 1; i <= n; i++) {result *= i;}return result;
}int fib_recursive(int n) {if (n < 2) {return n;}return fib_recursive(n - 1) + fib_recursive(n - 2);
}int fib_iterative(int n) {if (n < 2) {return n;}int a = 0, b = 1;int temp;for (int i = 2; i <= n; i++) {temp = a + b;a = b;b = temp;}return b;
}void hanoi(int n, char source, char auxiliary, char target) {if (n == 1) {printf("Move disk 1 from %c to %c\n", source, target);return;}hanoi(n - 1, source, target, auxiliary);printf("Move disk %d from %c to %c\n", n, source, target);hanoi(n - 1, auxiliary, source, target);
}int jump_floor(int n) 
{if (n <= 2) {return n;}int a = 1, b = 2;int temp;for (int i = 3; i <= n; i++) {temp = a + b;a = b;b = temp;}return b;
}

编译和运行一下：

gcc -o recursion_examples recursion_examples.c
./recursion_examples

最后，博主想说，理解这些经典问题，对于掌握算法设计和分析的基本思想至关重要。

结尾

往期回顾：

深入详解C语言数组：承上启下——从C语言数组基础到数据结构衔接

结语：感谢大家的阅读，记得给博主“一键四连”，感谢友友们的支持和鼓励！

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。
如若转载，请注明出处：http://www.pswp.cn/bicheng/94264.shtml
繁体地址，请注明出处：http://hk.pswp.cn/bicheng/94264.shtml
英文地址，请注明出处：http://en.pswp.cn/bicheng/94264.shtml

如若内容造成侵权/违法违规/事实不符，请联系英文站点网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

《LINUX系统编程》笔记p3

《LINUX系统编程》笔记p3

可重用函数不使用全局部变量&#xff0c;可以重复使用的函数.stat 命令作用&#xff1a;显示一个文件或文件夹的“元信息”。文件基本信息文件&#xff08;File&#xff09;&#xff1a;显示所查询对象的名称。大小&#xff08;Size&#xff09;&#xff1a;文件的大小&#xf…
阅读更多...
大模型0基础开发入门与实践：第3章 机器的“统计学”：机器学习基础概念扫盲

大模型0基础开发入门与实践：第3章 机器的“统计学”：机器学习基础概念扫盲

第3章 机器的“统计学”&#xff1a;机器学习基础概念扫盲 1. 引言 想象一下&#xff0c;你是一位古代的农夫&#xff0c;毕生的经验告诉你&#xff1a;乌云密布、燕子低飞&#xff0c;那么不久便会下雨。你并没有学习过气象学&#xff0c;也不懂大气压和水汽凝结的原理。你的“…
阅读更多...
Java调用Ollama（curl方式）

Java调用Ollama（curl方式）

1. 安装Ollama Search 2. 调用 相关依赖 <dependencies><dependency><groupId>org.apache.httpcomponents</groupId><artifactId>httpclient</artifactId><version>4.5.14</version></dependency><dependency>&…
阅读更多...
nodejs koa框架使用

nodejs koa框架使用

1: KOA 是express 打造的下一代web 开发框架提供更小更强的的核心功能&#xff0c;通过Promise 、async/await 进行异步编程&#xff0c;koa 可以不使用回调&#xff0c;解决了回调地狱的问题 blueBird 是nodejs 最出名的Primise 实现&#xff0c;除了实现标准的promise 之外&a…
阅读更多...
2025年图像处理与光学国际会议（ICIPO 2025）

2025年图像处理与光学国际会议（ICIPO 2025）

2025年图像处理与光学国际会议&#xff08;ICIPO 2025&#xff09; 2025 International Conference on Image Processing and Optics一、大会信息会议简称&#xff1a;ICIPO 2025 大会地点&#xff1a;中国北京 审稿通知&#xff1a;投稿后2-3日内通知 投稿邮箱&#xff1a;iac…
阅读更多...
Kubernetes 构建高可用、高性能 Redis 集群

Kubernetes 构建高可用、高性能 Redis 集群

k8s下搭建Redis高可用1. 部署redis服务创建ConfigMap创建 Redis创建 k8s 集群外部2. 创建 Redis 集群自动创建 redis 集群手动创建 redis 集群验证集群状态3. 集群功能测试压力测试故障切换测试4. 安装管理客户端编辑资源清单部署 RedisInsight控制台初始化控制台概览实战环境使…
阅读更多...
文件IO的基础操作

文件IO的基础操作

Java针对文件进行的操作:文件系统操作,File类(file类指定的路径,可以是一个不存在的文件)文件内容操作 : 流对象分为两类(1)字节流 以字节为基本的读写单位的 二进制文件 InputStream OutputStream(2)字符流 以字符为基本的读写单位的 …
阅读更多...
【模版匹配】基于深度学习

【模版匹配】基于深度学习

基于深度学习的模版匹配 概述 本报告整理了2024-2025年最新的、可直接使用的模板匹配相关论文、方法和开源代码实现。所有方法都提供了完整的代码实现和预训练模型&#xff0c;可以直接应用到实际项目中。 一、轻量级现代模板匹配框架 1.1 UMatcher - 4M参数的紧凑型模板匹…
阅读更多...
CMake进阶：Ninja环境搭建与加速项目构建

CMake进阶：Ninja环境搭建与加速项目构建

目录 1.引入Ninja的原因 2.Ninja 环境搭建&#xff08;跨平台&#xff09; 2.1.Linux系统安装 2.2.macOS 系统 2.3.Windows 系统 2.4.源码编译安装&#xff08;通用方案&#xff09; 3.Ninja 与构建系统配合&#xff1a;以 CMake 为例 4.加速构建的关键技巧 5.Ninja 与…
阅读更多...
开发避坑指南(35)：mybaits if标签test条件判断等号=解析异常解决方案

开发避坑指南(35)：mybaits if标签test条件判断等号=解析异常解决方案

异常信息 org.mybatis.spring.MyBatisSystemException: nested exception is org.apache.ibatis.builder.BuilderException: The expression orderInfo.idList evaluated to a null value.报错语句 <if test"orderInfo.queryFlag ! null and orderInfo.queryFlag sett…
阅读更多...
GitCode 疑难问题诊疗：全面指南与解决方案

GitCode 疑难问题诊疗：全面指南与解决方案

引言 在软件开发的动态领域中&#xff0c;GitCode 作为一款强大的分布式版本控制系统&#xff0c;已然成为团队协作与项目管理的基石。它赋予开发者高效管理代码版本、轻松实现并行开发以及顺畅协同合作的能力。然而&#xff0c;如同任何复杂的技术工具&#xff0c;在 GitCode…
阅读更多...
使用 JS 渲染页面并导出为PDF 常见问题与修复

使用 JS 渲染页面并导出为PDF 常见问题与修复

本文直击两个最常见的导出痛点&#xff0c;并给出可直接落地的诊断 修复方案&#xff08;适用于 html2canvas jsPDF ECharts/自绘 canvas 场景&#xff09;。 问题清单 问题 A&#xff1a;导出后图表模糊&#xff0c;线条与文字不清晰&#xff08;低分辨率&#xff09;。问题…
阅读更多...
【Java后端】【可直接落地的 Redis 分布式锁实现】

【Java后端】【可直接落地的 Redis 分布式锁实现】

可直接落地的 Redis 分布式锁实现&#xff1a;包含最小可用版、生产可用版&#xff08;带 Lua 原子解锁、续期“看门狗”、自旋等待、可重入&#xff09;、以及基于注解AOP 的无侵入用法&#xff0c;最后还给出 Redisson 方案对比与踩坑清单。一、设计目标与约束 获取锁&#x…
阅读更多...
数据结构 -- 链表--双向链表的特点、操作函数

数据结构 -- 链表--双向链表的特点、操作函数

双向链表的操作函数DouLink.c#include "DouLink.h" #include <stdio.h> #include <stdlib.h> #include <string.h>/*** brief 创建一个空的双向链表* * 动态分配双向链表管理结构的内存&#xff0c;并初始化头指针和节点计数* * return 成功返回指…
阅读更多...
Wireshark获取数据传输的码元速率

Wireshark获取数据传输的码元速率

一、Wireshark的物理层参数 Wireshark主界面可以看到数据发送时刻和长度&#xff1a; 这个时刻是Wireshark完整获取数据包的时刻&#xff0c;实际上就是结束时刻。 需要知道的是&#xff1a; Wireshark工作在数据链路层及以上&#xff0c;它能解码 以太网帧 / IP 包 / TCP…
阅读更多...
11.1.3 完善注册登录，实现文件上传和展示

11.1.3 完善注册登录，实现文件上传和展示

1、完善注册/登录 1. 涉及的数据库表单&#xff1a;user_info 2. 引用MySQL线程池&#xff0c;Redis线程池 3. 完善注册功能 4. 完善登录功能 2.1 涉及的数据库表单&#xff1a;user_info 重新创建数据库 #创建数据库 DROP DATABASE IF EXISTS 0voice_tuchuang;CREATE D…
阅读更多...
【Linux文件系统】目录结构

【Linux文件系统】目录结构

有没有刚进入Linux世界时&#xff0c;对着黑乎乎的终端&#xff0c;输入一个 ls / 后&#xff0c;看着蹦出来的一堆名字 like bin, etc, usr&#xff0c;感觉一头雾水&#xff0c;像是在看天书&#xff1f; 别担心&#xff0c;你不是一个人。Linux的文件系统就像一个超级有条理…
阅读更多...
螺旋槽曲面方程的数学建模与偏导数求解

螺旋槽曲面方程的数学建模与偏导数求解

螺旋槽曲面的数学描述 在钻头设计和机械加工领域，螺旋槽的几何建模至关重要。螺旋槽通常由径向截形绕轴做螺旋运动形成，其数学模型可通过参数方程和隐函数方程两种方式描述。 设螺旋槽的径向截形方程为： y=f(z)y = f(z)y=f(z) x=xcx = x_cx=xc​ 其中 xcx_cxc​ 为常数，…
阅读更多...
线性回归：机器学习中的基石

线性回归：机器学习中的基石

在机器学习的众多算法中&#xff0c;线性回归无疑是最基础也是最常被提及的一种。它不仅在统计学中占有重要地位&#xff0c;而且在预测分析和数据建模中也发挥着关键作用。本文将深入探讨线性回归的基本概念、评估指标以及在实际问题中的应用&#xff0c;并通过一个模拟的气象…
阅读更多...
编程刷题-资料分发1 图论/DFS

编程刷题-资料分发1 图论/DFS

P2097 资料分发 1 题目描述 有一些电脑&#xff0c;一部分电脑有双向数据线连接。 如果一个电脑得到数据&#xff0c;它可以传送到的电脑都可以得到数据。 现在&#xff0c;你有这个数据&#xff0c;问你至少将其输入几台电脑&#xff0c;才能使所有电脑得到数据。 输入格式 第…
阅读更多...
最新文章

Copyright @ 2022~2023