目录
一、哈希表
1.哈希算法
2.哈希碰撞
3.哈希表
4.哈希表相关操作
哈希表插入
哈希表遍历
元素查找
哈希表销毁
二、排序算法
1. 排序算法对比
2. 排序算法实现
冒泡排序
选择排序
插入排序
希尔排序
快速排序
三、查找算法
1. 查找算法对比
2. 查找算法实现
顺序查找
折半查找(二分查找)
一、哈希表
1.哈希算法
- 将数据通过哈希算法映射成一个键值,存取都在同一个位置实现数据的高效存储和查找,将时间复杂度尽可能降低至O(1)
- 哈希算法是不固定的,需要选择一个合适的哈希算法,才能映射成一个键值
2.哈希碰撞
多个数据通过哈希算法得到的键值相同,称为产生哈希碰撞
3.哈希表
- 构建一个哈希表,存放0~100之间的数据
- 哈希算法的选择:
将0~100之间的数据的个位作为键值
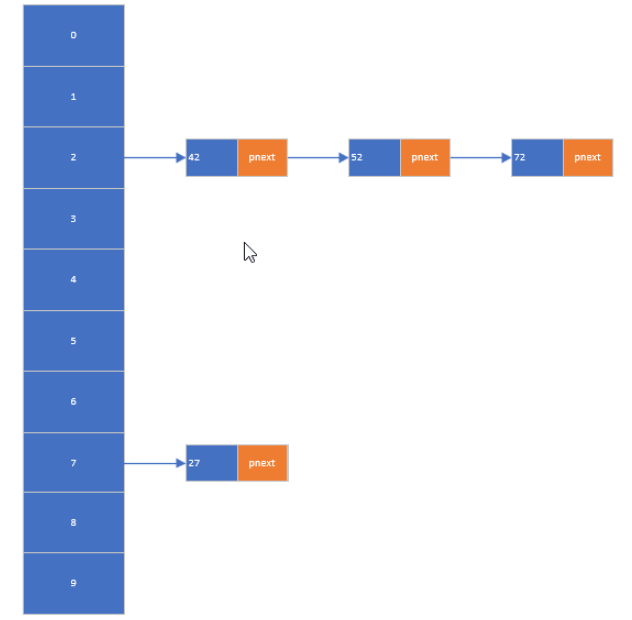
哈希表通过哈希函数实现高效存取,需解决哈希碰撞
4.哈希表相关操作
哈希表插入
#define INDEX 10 // 假设哈希表大小为10(0-9)
linknode *phashtable[INDEX] = {NULL}; // 哈希表数组/* 哈希表插入函数 */
int insert_hashtable(int tmpdata) {int key = 0;linknode **pptmpnode = NULL; // 二级指针用于修改链表节点linknode *pnewnode = NULL;// 计算哈希键值(取数据的个位)key = tmpdata % INDEX;// 找到插入位置(保持链表有序)for (pptmpnode = &phashtable[key]; *pptmpnode != NULL && (*pptmpnode)->data < tmpdata; pptmpnode = &(*pptmpnode)->pnext) {// 循环移动指针至合适位置}// 申请新节点pnewnode = malloc(sizeof(linknode));if (NULL == pnewnode) {perror("fail to malloc");return -1;}// 插入新节点pnewnode->data = tmpdata;pnewnode->pnext = *pptmpnode;*pptmpnode = pnewnode;return 0;
}
哈希表遍历
/* 遍历哈希表所有元素 */
int show_hashtable(void) {int i = 0;linknode *ptmpnode = NULL;for (i = 0; i < INDEX; i++) {printf("%d:", i); // 打印键值ptmpnode = phashtable[i];while (ptmpnode != NULL) {printf("%2d ", ptmpnode->data); // 打印链表元素ptmpnode = ptmpnode->pnext;}printf("\n");}return 0;
}
元素查找
/* 查找哈希表中的元素 */
linknode *find_hashtable(int tmpdata) {int key = 0;linknode *ptmpnode = NULL;key = tmpdata % INDEX; // 计算键值ptmpnode = phashtable[key];// 遍历对应链表查找元素while (ptmpnode != NULL && ptmpnode->data <= tmpdata) {if (ptmpnode->data == tmpdata) {return ptmpnode; // 找到返回节点地址}ptmpnode = ptmpnode->pnext;}return NULL; // 未找到返回NULL
}
哈希表销毁
/* 销毁哈希表,释放所有节点 */
int destroy_hashtable(void) {int i = 0;linknode *ptmpnode = NULL;linknode *pfreenode = NULL;for (i = 0; i < INDEX; i++) {ptmpnode = phashtable[i];pfreenode = phashtable[i];while (ptmpnode != NULL) {ptmpnode = ptmpnode->pnext;free(pfreenode); // 释放当前节点pfreenode = ptmpnode;}phashtable[i] = NULL; // 置空数组元素}return 0;
}
二、排序算法
排序算法中,冒泡、选择、插入排序适用于小规模数据;希尔、快速排序适用于大规模数据,其中快速排序性能最优(平均 O (nlogn))
1. 排序算法对比
| 算法 | 时间复杂度 | 稳定性 | 核心思想 |
|---|---|---|---|
| 冒泡排序 | O(n²) | 稳定 | 相邻元素比较,大元素后移,重复 n-1 次 |
| 选择排序 | O(n²) | 不稳定 | 每次从剩余元素中找最小值,与当前位置交换 |
| 插入排序 | O(n²) | 稳定 | 将元素插入到已排序序列的合适位置,类似整理扑克牌 |
| 希尔排序 | O(n^1.3) | 不稳定 | 按步长分割数组为子序列,分别插入排序,逐步减小步长至 1 |
| 快速排序 | O(nlogn) | 不稳定 | 选基准值,将数组分为小于和大于基准的两部分,递归排序两部分 |
2. 排序算法实现
冒泡排序
核心思想是通过相邻元素的比较和交换,使较大的元素逐步 “浮” 到数组的末尾。具体来说,相邻的两个元素比较,大的向后走,小的向前走,循环找出数组中 len-1 个较大的值,最终实现整个数组的有序排列
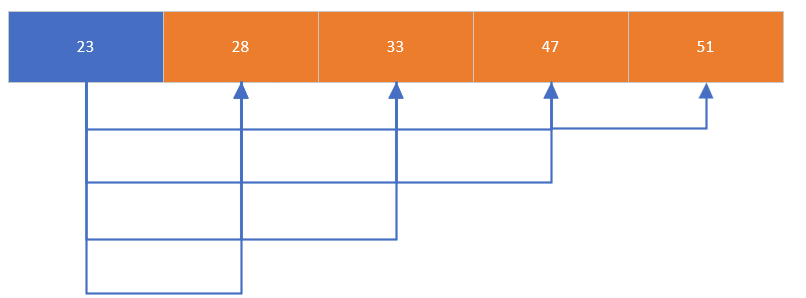
/* 冒泡排序:相邻元素比较交换,大元素后移 */
int bubble_sort(int *parray, int len) {int i = 0;int j = 0;int tmp = 0;for (j = 0; j < len - 1; j++) { // 控制轮次for (i = 0; i < len - 1 - j; i++) { // 每轮比较次数递减if (parray[i] > parray[i + 1]) {// 交换元素tmp = parray[i];parray[i] = parray[i + 1];parray[i + 1] = tmp;}}}return 0;
}
选择排序
核心思想是从前到后在未排序元素中寻找最小值,然后将找到的最小值与未排序部分的前面元素进行交换。通过找到 len-1 个最小值,最后剩下的一个元素自然就是最大值,从而完成排序
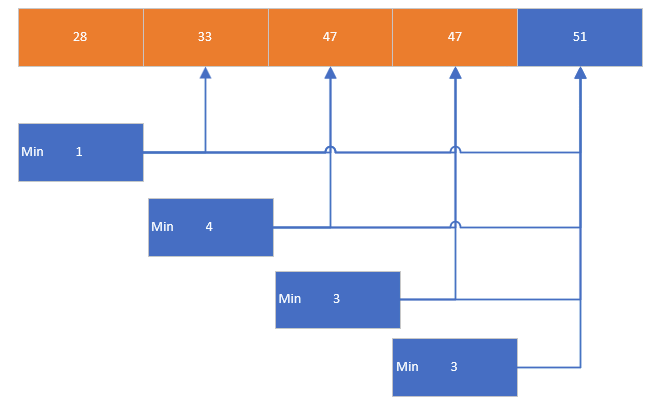
/* 选择排序:找最小值并交换到当前位置 */
int select_sort(int *parray, int len) {int i = 0;int j = 0;int tmp = 0;int min = 0; // 最小值索引for (j = 0; j < len - 1; j++) {min = j; // 假设当前位置为最小值for (i = j + 1; i < len; i++) {if (parray[i] < parray[min]) {min = i; // 更新最小值索引}}// 交换最小值到当前位置if (min != j) {tmp = parray[min];parray[min] = parray[j];parray[j] = tmp;}}return 0;
}
插入排序
核心思想是将数组中的每个元素逐个插入到已排序的数列中。首先取出要插入的元素,然后依次和前面的元素比较,比该元素大的元素向后移动,直到遇到前一个元素比要插入的元素小,或者到达有序数列的开头时停止,最后将该元素插入到合适位置
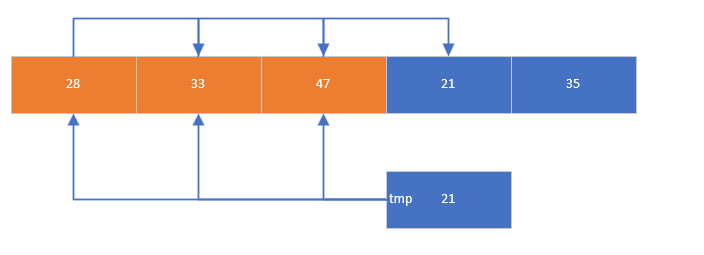
/* 插入排序:将元素插入已排序序列的合适位置 */
int insert_sort(int *parray, int len) {int tmp = 0; // 待插入元素int i = 0;int j = 0;for (j = 1; j < len; j++) {tmp = parray[j]; // 取出待插入元素// 找到插入位置for (i = j; i > 0 && tmp < parray[i - 1]; i--) {parray[i] = parray[i - 1]; // 元素后移}parray[i] = tmp; // 插入元素}return 0;
}
希尔排序
核心思想是通过选择不同的步长,将数组拆分成若干个小的子数组,对每个子数组进行插入排序。当若干个子数组成为有序数列后,数组中的数据会大致有序,最后再对整体进行一次插入排序,以完成整个数组的排序

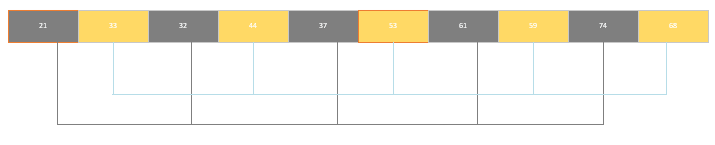

/* 希尔排序:按步长分割子序列,逐步缩小步长 */
int shell_sort(int *parray, int len) {int step = 0; // 步长int j = 0;int i = 0;int tmp = 0;// 步长初始为len/2,每次减半至0for (step = len / 2; step > 0; step /= 2) {// 对每个子序列进行插入排序for (j = step; j < len; j++) {tmp = parray[j];for (i = j; i >= step && tmp < parray[i - step]; i -= step) {parray[i] = parray[i - step]; // 元素后移}parray[i] = tmp; // 插入元素}}return 0;
}
快速排序
核心思想是选择数组左边的元素作为键值,从数组后面找一个比键值小的元素放到前面,再从前面找一个比键值大的元素放到后面,最后将键值放到中间位置。如果左右两边还有元素,则递归调用快速排序对两边元素进行排序
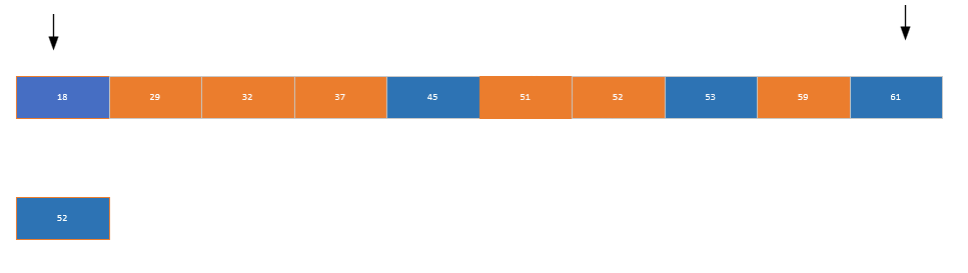
/* 快速排序:分治思想,以基准值分割数组 */
int quick_sort(int *parray, int low, int high) {int key = 0; // 基准值int i = low; // 左指针int j = high; // 右指针if (low >= high) {return 0; // 递归终止条件}key = parray[low]; // 选最左元素为基准值while (i < j) {// 从右向左找小于基准值的元素while (i < j && parray[j] >= key) {j--;}if (i < j) {parray[i] = parray[j]; // 移至左指针位置}// 从左向右找大于基准值的元素while (i < j && parray[i] <= key) {i++;}if (i < j) {parray[j] = parray[i]; // 移至右指针位置}}parray[i] = key; // 基准值归位// 递归排序左半部分if (i - 1 > low) {quick_sort(parray, low, i - 1);}// 递归排序右半部分if (i + 1 < high) {quick_sort(parray, i + 1, high);}return 0;
}
三、查找算法
查找算法中,折半查找效率远高于顺序查找,但依赖有序数据
1. 查找算法对比
| 算法 | 时间复杂度 | 适用场景 | 核心思想 |
|---|---|---|---|
| 顺序查找 | O(n) | 无序或小规模数据 | 从前往后依次遍历,逐个比较 |
| 折半查找 (二分查找) | O(logn) | 有序数组 | 每次取中间元素比较,缩小查找范围至左半或右半部分 |
2. 查找算法实现
顺序查找
从数组的起始位置开始,逐个将元素与要查找的目标值进行比较,若找到与目标值相等的元素,则查找成功;若遍历完整个数组都没有找到,则查找失败
/* 顺序查找:遍历数组逐个比较 */
int seq_search(int *parray, int len, int target) {int i = 0;for (i = 0; i < len; i++) {if (parray[i] == target) {return i; // 找到返回索引}}return -1; // 未找到返回-1
}
折半查找(二分查找)
针对有序数组,先计算中间位置,将中间位置的元素与目标值比较。如果目标值等于中间元素,则查找成功;如果目标值大于中间元素,则在数组的右半部分继续查找;如果目标值小于中间元素,则在数组的左半部分继续查找,重复此过程直至找到目标值或确定查找范围为空
/* 折半查找:仅适用于有序数组 */
int binary_search(int *parray, int low, int high, int target) {int mid = 0;if (low > high) {return -1; // 查找失败}mid = (low + high) / 2; // 计算中间索引if (parray[mid] == target) {return mid; // 找到返回索引} else if (target > parray[mid]) {// 目标在右半部分,递归查找return binary_search(parray, mid + 1, high, target);} else {// 目标在左半部分,递归查找return binary_search(parray, low, mid - 1, target);}
}









:Vue3响应式编程中this绑定机制与解决方案)

的使用——以NDVI去水体为例)




flutter命令行工具)


