一、说明

动态规划似乎针对问题很多，五花八门，似乎每一个问题都有一套具体算法。其实不是的，动态规划只有两类：1）针对图的路径问题 2）针对一个序列的问题。本篇讲动态规划针对序列的算法范例。

二、动态规划解决的问题

1 动态规划针对什么问题？
1）从0到N是个规模膨胀的递归问题。
2）如果$f(N-1)$有解，那么可以推导出$f(N)$的解。

2 动态规划可以解决的问题特点：
1）按照规模递增的关系，凡是问题$f(N)$的解依赖于$f(N-1)$的解。
2）算法从$f(0)$出发，能推导出$f(1)$的解，然后正向求解。

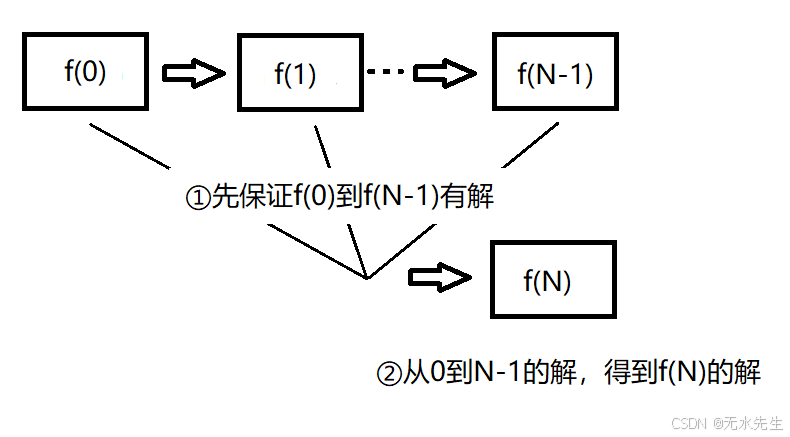
3 两类动态规划的问题
动态规划似乎针对问题很多，五花八门，每一个问题都有一套具体算法。其实不是的，动态规划只有两类：1）针对图的路径问题 2）针对一个序列的问题。
本篇讲动态规划针对序列的算法范例。

三、动态规划解决最大上升子序列问题

3.1 问题描述

问题提出：对于序列$a_1,a_2,...a_n$找到一个最长的递增序列$a_{i_1},a_{i_2}...a_{i_k}$,其中，$i_1<i_2,...<i_n$且，$a_{i_1}<a_{i_2}...<a_{i_k}$
示例：

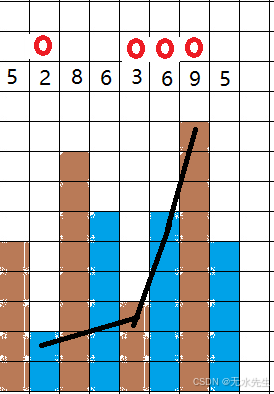
对于序列【 5， 2， 8 ，6， 3， 6， 9， 5 】的最长上升子序列长度：

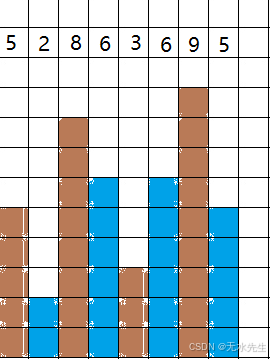
答案是：
【2，3，6，9】

3.2 算法描述

法则：
LIS[n]=1+max{LIS[n−1]∣k<n,A[k]<A[n]}LIS[n]=1+max\{LIS[n-1]|k<n,A[k]<A[n]\}LIS[n]=1+max{LIS[n−1]∣k<n,A[k]<A[n]}
下面对一个序列进行逐步解释：
求下列序列的最大上升子序列：
【 5， 2， 8 ，6， 3， 6， 9， 5 】

解：先命名两个序列iem和lenght，分别存储当前值和对应长度。
建立iem序列：【 5， 2， 8 ，6， 3， 6， 9， 5 】
lenght序列：
【 1， 1， 1 ，1， 1， 1， 1， 1 】

• 预先给出每个元素初始长度为“1”

开始扫描：
step1：对序列ltem【0】元素进行扫描，由于没有前序，所以【0】的长度依然是1：length【0】=1

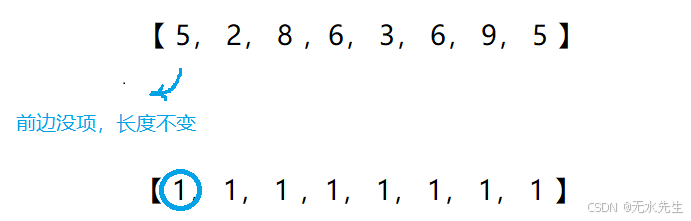
step2：对序列ltem【1】元素进行扫描，由于前序是5（大于本地的2），所以【1】的长度依然是1：length【1】=1

step3：对序列item【2】元素进行扫描，由于前序是5和2，小于本地的8，所以len_max（length【0】，length【1】）=1，所以，length【2】=len_max+length【2】=2

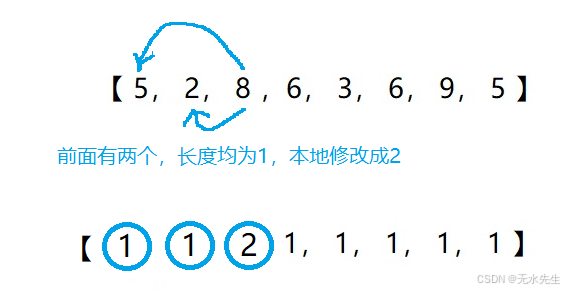
step4：对序列item【3】元素进行扫描，本地的6，小于本地6的前序是5和2，所以len_max（length【0】，length【1】）=1，所以，length【3】=len_max+length【3】=2

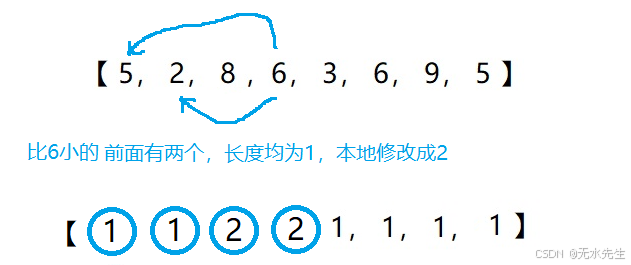
step5：对序列item【4】元素进行扫描，本位值3，小于本地3的前序是2，所以len_max（length【2】）=1，所以，length【4】=len_max+length【4】=2

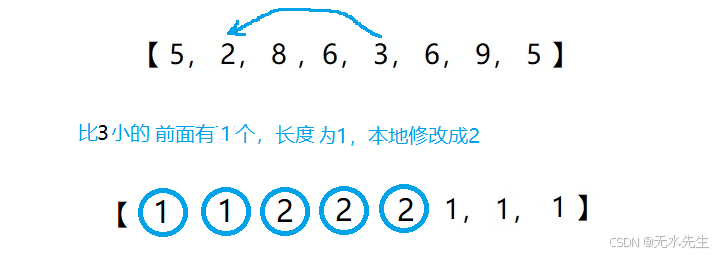
step6：对序列item【5】元素进行扫描，本位值6，小于本地6的前序是【5，2.3】，所以len_max（length【0】，length【1】，length【4】）=2，所以，length【5】=len_max+length【5】=3

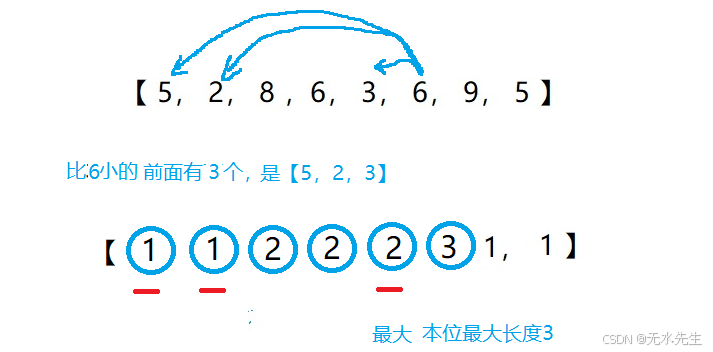
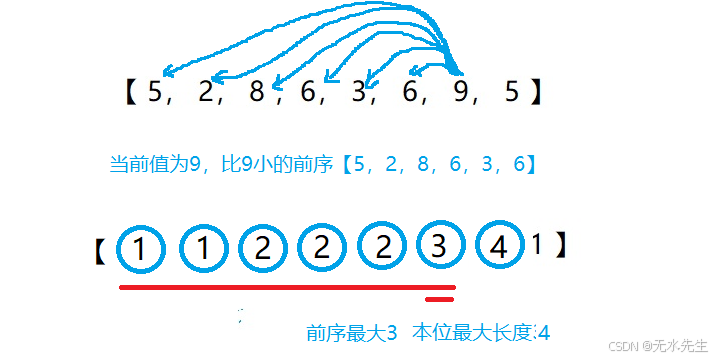
step7：对序列item【6】元素进行扫描，本位值9，小于本地6的前序是【5，2，8，6，3，6】，所以len_max（length【0】，length【1】，length【2】…）=3，所以，length【6】=len_max+length【6】=4

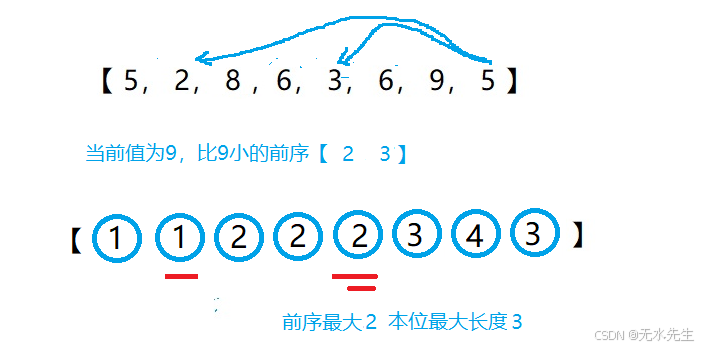
step8：对序列item【7】元素进行扫描，本位值5，小于本地5的前序是【2，3】，所以len_max（length【2】，length【3】）=2，所以，length【7】=len_max+length【7】=3

3.3 算法代码

用python给出整个代码：

def lis(A):L =[1]*len(A)for i in range(1,len(L)):subproblem = [ L[k] for k in range(i) if A[k]<A[i]]L[i] = 1 +max(subproblem,default=0)return max(L,default=0)