LeetCode 322. 零钱兑换  

思路1： 回溯算法可以做，只要存储数组的最小长度即可，但可能会超时。

思路2:   相当于是求最大价值的相反面，另外一个物品可以使用多次，因此是个完全背包。因此这是个完全背包的求最小价值类型题目。

注意：

• 区分达到背包容量的方式 和 区分背包容量下的最大/最小价值，前者(方式)是通过累加递推，后者(价值)是通过max和min函数来递推。
• 在求最大价值时候，由于每个元素是正数，因此dp数组是初始化为0。max()函数可以有效进行覆盖。但本题是求最小价值，因此dp数组需要初始化为float('inf')即正无穷，这样的话min()函数可以有效进行覆盖。另外，dp[0]是特殊情况，需要根据情况进行手动修改。

class Solution(object):def coinChange(self, coins, amount):""":type coins: List[int]:type amount: int:rtype: int"""## 每种硬币的数量是无限的, 因此是个完全背包。## 可以凑成总金额所需的 最少的硬币个数。关键在于最少的递推公式是什么. 最少的硬币个数不就是求最大价值的相反面吗## 求元素的数目，与价值有关，因此背包和物品的排列顺序可以任意。## 1. dp数组定义。dp[j]表示总金额（背包容量）为j下的最少硬币个数（最少物品数量）dp = [float('inf')] * (amount + 1)      ## 求最大价值的时候，这里是初始化为0## 现在是求最小价值，这里要初始化为最大值## 2. dp初始化# dp[0] = 1       ### 不取也是一种方式。但这里不是求方式，而是求个数dp[0] = 0         ### 因此amount = 0 的时候dp[0]是0个硬币## 3. 递推公式# dp[j] = min(dp[j], (dp[j-coins[i]] + 1)]  ## 每进行一次加法，就证明多了一个硬币## 4. 遍历顺序。 跟组合和排列无关，因此背包和物品的排列顺序可以任意。for i in range(len(coins)):for j in range(coins[i], len(dp)):dp[j] = min(dp[j], (dp[j-coins[i]] + 1) )## 5. 打印 dpif dp[amount] == float('inf'):      ## 硬币的种类凑不到总金额return -1return dp[amount]

LeetCode 279.完全平方数 

思路：

1. 先根据输入的数获取一个物品数组，这个物品长度最短为 math.sqrt(target) 。当math.sqrt(target)平方根为整数时，此时表示target可以基于math.sqrt(target)的完全平方数一次得到。若不是，则需要列出小于math.sqrt(target)的所有可能整数的完全平方数，这个数组就是物品。

2. 搞定物品后其实这道题有差不多有思路了，另外的，递推公式记得+1，因为是要求数量，没加1的话就变成了求构成的完全平方数中的最小元素。

Code:

import math
class Solution(object):def numSquares(self, n):""":type n: int:rtype: int"""### 最少数量即最小价值，物品背包遍历先后顺序不影响### 由于第一个物品可以被用多次，因此是完全背包类型### 物品是一个正整数组 [1,2,3,...,n]### 将上述正整数组平方得到一个正整数组的平方数组[2,4,9,...,n^2]### 最大背包容量为nnums = [0]* (int(math.sqrt(n)))for i in range(len(nums)):nums[i] = (i+1)*(i+1)       ### 起始坐标是从0开始，要右移一位# 1. dp 定义，dp[j]，整数为j下，和为j的完全平方数的最少数量dp = [float('inf')] * (n+1)# 2. dp 初始化    dp[0] = 0   ## 0 本身可以不通过别人平方相加得到# 3. 递推公式# dp[j] = min(dp[j], dp[j-nums[i]])# dp[j] = min(dp[j], dp[j-nums[i]]+1)   ## 衡量的是数量因此要加1，而不是上述这个，这个是求其中的一个最小元素。# 4. 遍历顺序for i in range(len(nums)):              # 先遍历物品for j in range(nums[i], len(dp)):   # 再遍历背包dp[j] = min(dp[j], dp[j-nums[i]]+1)# 5. 打印dp# print(dp)return dp[n]

LeetCode 139.单词拆分

类似题目：

LeetCode 131: 分割回文串。 这道题是字符串拆分成回文串，而本题是判断字典中的单词能否组成字符串。

思路：

这道题偏难，即考究字符串的操作，又考究了双指针，结合双指针来设计dp数组。通过一个双指针来遍历指针之间的子字符串是否存在于字典中来进行判断，并将判断结果更新到dp数组中。如下所示：

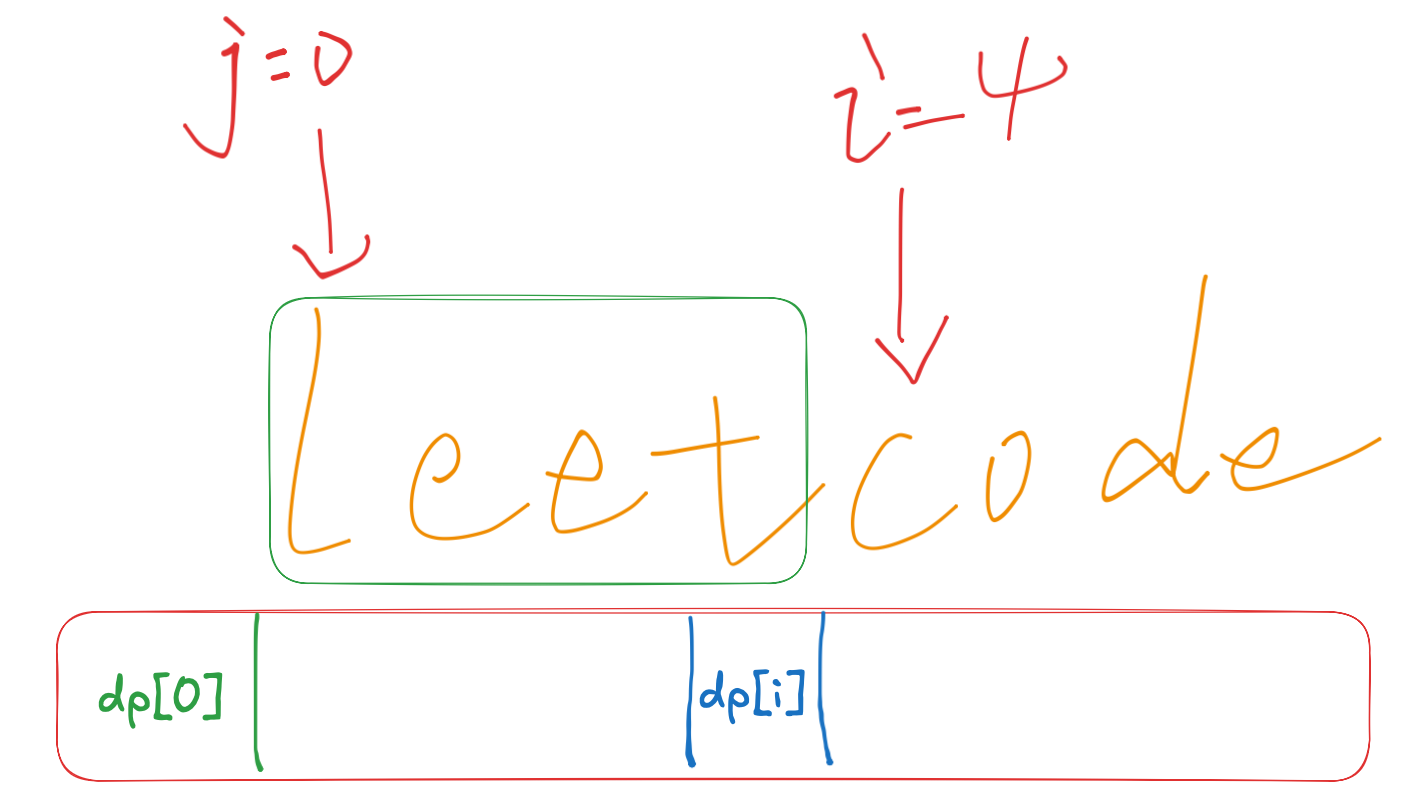
根据字符串的关系去更新dp数组是关键，下标多会有点乱，要理清dp的下标含义和i,j指向字符串时又表达什么意思。递推公式那里要搞懂。

• 确定递推公式

如果确定dp[j] 是true，且 [j, i] 这个区间的子串出现在字典里，那么dp[i]一定是true。（j < i ）。

所以递推公式是 if([j, i] 这个区间的子串出现在字典里 && dp[j]是true) 那么 dp[i] = true。

Code

class Solution(object):def wordBreak(self, s, wordDict):""":type s: str:type wordDict: List[str]:rtype: bool"""### 物品可以被多次使用，因此是完全背包。### 在数字数组中，求和问题可以通过相加来判断。关键：但在字符串中，如何判断字典中的单词拼接起来能否构成该target字符串# 1. dp数组定义。dp[j]表示长度为j的字符串能否由单词表中的单词构成。dp = [False] * (len(s) + 1)     # 2. dp数组初始化。先默认不能由单词表中的单词构成。dp[0] = True            ## 第一个表示空字符串## 虽题目默认了不会有空字符串，但dp[0]需要初始化为True，如果初始化为False, 则后面无法进行递推，所得到的都会是False# 3. 递推公式。关键：递推公式是什么？# if dp[j] == True and [j,i] in word_dict:     ## 如果字符串中的前i个已匹配，且[i，j]这个位置存在子字符串。#       dp[i] = True# 4. 遍历顺序。单词的构成涉及到排列，因此是先遍历背包再遍历物品。for i in range(1, len(dp)):    ## 先遍历背包for j in range(i):         ## 再遍历物品, j始终都是在i的左边，j去追赶i, j和i的这段距离内的子字符串sub_string = s[j:i]    ## j位置开始(包括j)到i(不包括i)的这段子字符串。 i-j这段区间有i-j个字符if dp[j] == True and sub_string in wordDict:dp[i] = True       ## j + i - j = i，前j个字符可行，现在从第j开始的i-j个字符可行，因此前i个字符可行# break             ## 不break也可以，break是对一些多余的循环进行剪枝# 5. 打印dp数组return dp[len(s)]

多重背包基础

• 01背包是一个物品只能用一次
• 完全背包是一个物品能用无数次
• 多重背包是一个物品能用x次

涉及多重背包的题目较少，如遇到的话，将其转化为01背包就行。如下所示：

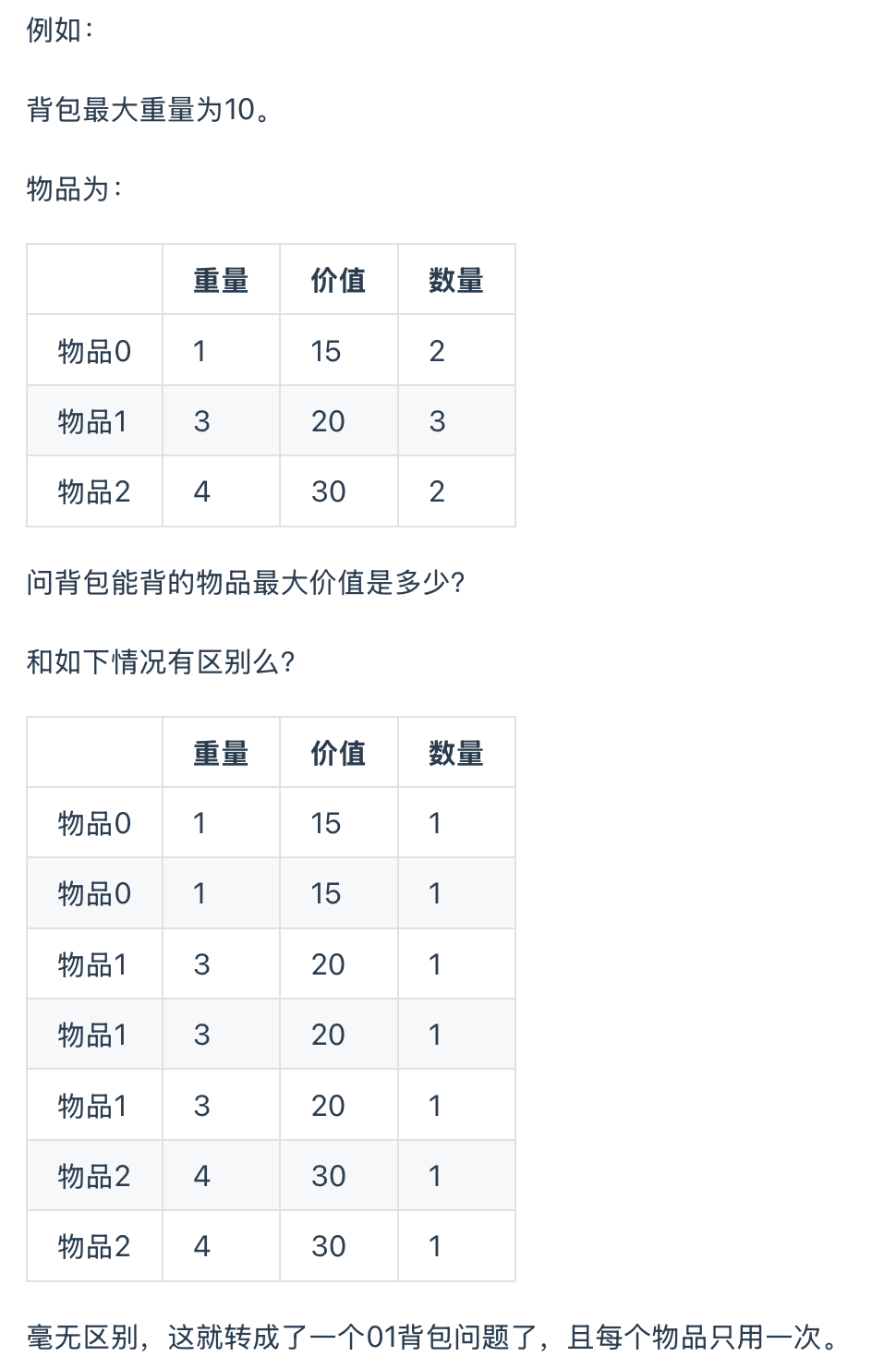
56. 携带矿石资源

思路1：

将多重背包转换为01背包进行解决。

需要注意如何将多重转换为01问题，另外01问题在遍历背包时需要注意顺序。

Code

bagroom, category = input().split()
bagroom, category = int(bagroom), int(category)weight = []
for x in input().split():weight.append(int(x))price = []
for x in input().split():price.append(int(x))nums = []
for x in input().split():nums.append(int(x))for i in range(len(nums)):      ### 将多重背包转换为01背包处理, 但如果nums数目过大的话，会导致01背包中物品数组的长度很大，进而导致超时。count = nums[i]while count != 1:weight.append(weight[i])price.append(price[i])count -= 1# 1. dp定义，dp[j]表示背包容量为j下背包的最大价值
dp = [0] * (bagroom + 1)# 2. dp初始化，初始化为0
# 3. 递推公式。dp[j] = max(dp[j], dp[j-weight[i]+price[i]])
# 4. 遍历顺序
for i in range(len(weight)):                ## 先物品再背包容量for j in range(len(dp)-1, weight[i]-1, -1): ## 01背包这里要逆序遍历，确保每个物品只用一次dp[j] = max(dp[j], dp[j-weight[i]]+price[i])
# 5. 打印dp数组
# print(dp)
print(dp[bagroom])

思路2：

对物品的数目也进行一个循环操作，来判断物品的数目添加多少时可以达到最大价值。其实就是多加了个循环来判断当前物品要装多少个，来得到最大价值。

Code:

bagroom, category = input().split()
bagroom, category = int(bagroom), int(category)weight = []
for x in input().split():weight.append(int(x))price = []
for x in input().split():price.append(int(x))nums = []
for x in input().split():nums.append(int(x))# 1. dp定义，dp[j]表示背包容量为j下背包的最大价值
dp = [0] * (bagroom + 1)# 2. dp初始化，初始化为0
# 3. 递推公式。dp[j] = max(dp[j], dp[j-k*weight[i]+k*price[i]])
# 4. 遍历顺序
for i in range(len(weight)):                ## 先物品再背包容量for j in range(len(dp)-1, weight[i]-1, -1): ## 这里要逆序遍历，确保每个物品只用一次for k in range(1, nums[i]+1):   ## nums[i]+1 确保最后一个数可以被遍历到。range是左闭右开。if j < k*weight[i]:     ## 背包容量不够，那再大的k可以不用遍历了breakdp[j] = max(dp[j], dp[j-k*weight[i]]+ k*price[i])# 5. 打印dp数组
# print(dp)
print(dp[bagroom])