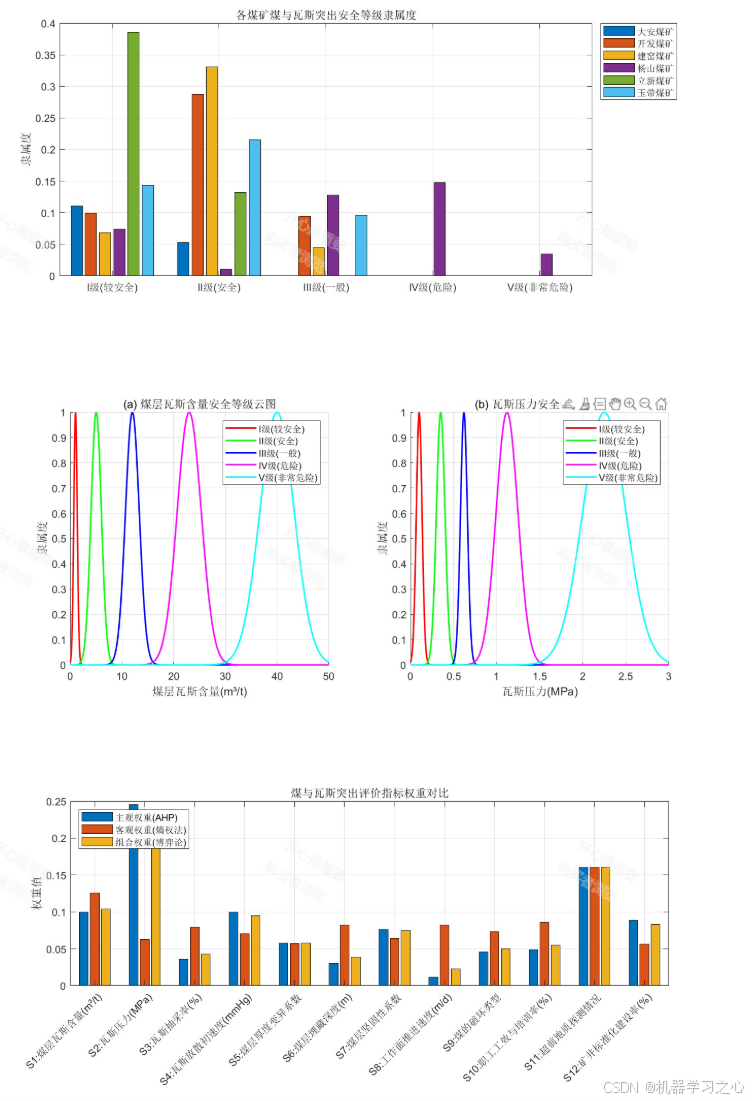
在这里插入图片描述

MATLAB基于博弈论组合赋权-云模型的煤与瓦斯突出危险性评价

1. 问题背景与核心目标

背景：煤与瓦斯突出是煤矿生产中的一种极其复杂的动力灾害，其发生机理复杂，影响因素众多（如地应力、瓦斯压力、煤体物理属性等）。对其进行准确、科学的危险性评价是煤矿安全管理的重中之重。
传统方法的局限性：
1. 权重确定问题：传统方法常采用主观赋权法（如AHP）或客观赋权法（如熵权法）。主观赋权依赖专家经验，可能带有偏见；客观赋权完全依赖数据，有时与实际情况不符。单一使用任何一种方法都有失偏颇。
2. 评价模型问题：传统模型多采用模糊综合评判或确定性数学模型，难以同时处理评价指标模糊性（“多大压力算高？”）和随机性（“同一指标值可能属于不同危险等级”）共存的問題。
核心目标：构建一个更科学、更合理的评价模型，既能综合主客观权重信息，又能处理评价中的模糊性和随机性，从而实现对煤与瓦斯突出危险性的精准评价。

2. 整体模型框架

该模型的构建主要分为三个阶段：

指标体系建立：科学选取评价指标。
组合权重确定：运用博弈论思想，寻找主客观权重的最优均衡组合。
云模型综合评价：通过云模型生成各等级的标准云，并计算待评样本相对于各等级的隶属度，最终确定其危险等级。

流程图为：
确立评价指标体系 -> 计算主客观权重 -> 博弈论组合赋权 -> 构建标准云模型 -> 计算综合隶属度 -> 确定突出危险性等级

3. 详细步骤分解

步骤一：建立煤与瓦斯突出危险性评价指标体系

选取指标：根据《防治煤与瓦斯突出细则》、理论和实践经验，选取代表性强的指标。通常包括：
- 瓦斯相关：瓦斯压力 §、瓦斯放散初速度 (ΔP)、煤的坚固性系数 (f)
- 地质相关：开采深度 (H)、煤层倾角 (α)、地质构造复杂程度
- 应力相关：地应力大小、钻屑量 (S)
划分危险等级：通常划分为4个等级：I级（无危险）、II级（弱危险）、III级（中等危险）、IV级（强危险）。并为每个指标确定各等级的取值范围（上限和下限）。

步骤二：基于博弈论的组合赋权

这是模型的核心创新点之一，目的是得到一组“共识权重”。

计算主观权重 (W_sub)：
- 采用层次分析法 (AHP)。邀请专家构造判断矩阵，通过计算特征向量和一致性检验，得到主观权重向量 W_sub。
计算客观权重 (W_obj)：
- 采用熵权法 (Entropy Weight Method)。根据各指标值的离散程度（数据本身的变异程度）来计算权重。信息熵越小，指标变异程度越大，其提供的信息量越多，权重越大。得到客观权重向量 W_obj。
博弈论组合赋权：
- 基本思想：将主观权重和客观权重视为两个“参与者”，它们通过博弈寻求一种对双方都最满意的妥协方案，即最优组合权重。
- 数学过程：
  a. 构造一个可能的权重集合：W = α * W_sub + β * W_obj，其中 α 和 β 是线性组合系数。
  b. 目标是使组合权重 W 与 W_sub 和 W_obj 的离差极小化。
  c. 根据博弈论，优化模型为：
  min || α·W_sub^T + β·W_obj^T - W_sub ||_2
  min || α·W_sub^T + β·W_obj^T - W_obj ||_2
  d. 根据最优化一阶导数条件，可转化为求解线性方程组：
  [ W_sub·W_sub^T W_sub·W_obj^T ] [α] = [ W_sub·W_sub^T ]
  [ W_obj·W_sub^T W_obj·W_obj^T ] [β] [ W_obj·W_obj^T ]
  e. 求解出 α 和 β，并进行归一化处理：α* = α / (α+β), β* = β / (α+β)。
  f. 计算最终的最优组合权重：W_comb = α* * W_sub + β* * W_obj。

步骤三：基于云模型的危险性评价

这是模型另一个核心创新点，用于处理模糊性和随机性。

构建标准云模型：
- 云模型用三个数字特征来表征一个概念：期望 (Ex)、熵 (En)、超熵 (He)。
- 对于每个评价指标的每个危险等级，都构建一个标准云。
- 计算方法（以“瓦斯压力P”的“IV级（强危险）”为例）：
  - 设其标准区间为 [P_min, P_max]。
  - Ex = (P_min + P_max) / 2 （区间的中心点，是最能代表该等级的值）
  - En = (P_max - P_min) / 6 （区间边界的模糊性，3En 区间包含了99.7%的云滴）
  - He 是一个常数，通常根据经验设定，表示熵的不确定性（即云的厚度）。
- 重复此过程，为所有指标的所有等级构建标准云。
生成待评样本的确定度：
- 对于一个待评价的煤矿样本，我们测得了其各项指标的具体数值 (x1, x2, ..., xn)。
- 对于每一个指标 xi，计算它隶属于各个危险等级标准云的确定度（隶属度）。
- 计算公式：μ_k(xi) = exp[ - (xi - Ex_ik)^2 / (2 * (En_ik')^2) ]
  - 其中，En_ik' 是一个以 En_ik 为期望、He_ik 为标准差的正态随机数。这一步引入了随机性，使得每次计算都有微小差异，更符合实际。
- 通常为了消除随机性影响，会重复计算多次（如1000次）并取平均确定度。
计算综合隶属度与等级判定：
- 利用步骤二得到的组合权重 W_comb，计算待评样本隶属于各个危险等级 k 的综合隶属度 B_k。
  B_k = Σ (w_i * μ_k(xi)) （i 从1到n，n是指标数量）
- 根据最大隶属度原则，选择 B_k 值最大的那个等级 k 作为该样本的最终煤与瓦斯突出危险性评价等级。

4. 模型优势与创新点

权重的科学性与均衡性：博弈论组合赋权巧妙地兼顾了专家的先验知识（主观权重）和数据隐含的统计规律（客观权重），避免了单一赋权的片面性，使权重分配更合理、更具说服力。
评价结果的鲁棒性：云模型同时考虑了事物的模糊性（等级边界不清晰）和随机性（指标测量误差、波动），比传统的模糊数学或确定性模型更能反映客观现实，评价结果更准确、可靠。
可视化的直观性：云模型生成的标准云图和综合评价云图非常直观，易于理解各指标和整体所处的危险状态。
普适性：该方法论具有通用性，稍加修改即可应用于其他领域的多指标综合评价问题，如地下水污染评价、地质灾害预警、金融风险评估等。