7.11 RSK算法

在对称函数理论中，有一个非凡的组合对应关系，称为RSK算法。（关于缩写RSK的含义以及其他名称，请参阅本章末尾的注释。）这里我们仅介绍RSK算法的最基本性质，从而能够给出舒尔函数一些基本性质的组合证明。当然，这些结果也可以通过纯代数方法证明，但在枚举组合学的教材中，我们更倾向于组合证明。

RSK算法的基本操作是将一个正整数 $k$ 行插入到一个非斜的SSYT $P=(P_{ij})$ 中，记作 $P\leftarrow k$。操作 $P\leftarrow k$ 的定义如下：设 $r$ 是满足 $P_{1,r-1}\le k$ 的最大整数（如果 $P_{11}>k$，则令 $r=1$）。如果 $P_{1r}$ 不存在（即 $P$ 有 $r-1$ 列），则直接将 $k$ 放在第一行的末尾。插入过程停止，得到的SSYT即为 $P\leftarrow k$。另一方面，如果 $P$ 至少有 $r$ 列，即 $P_{1r}$ 存在，则将 $P_{1r}$ 替换为 $k$。被替换的元素 $P_{1r}:=k^{\prime }$ 会被“挤入”第二行，即按照上述插入规则将 $k^{\prime }$ 插入到 $P$ 的第二行中。继续这一过程，直到某个元素被插入到某一行的末尾（可能是新行的第一个元素）。最终得到的数组即为 $P\leftarrow k$。

7.11.1 示例

设

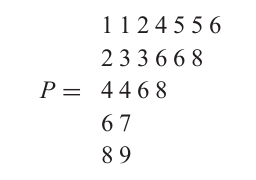
则 $P\leftarrow 4$ 的结果如下所示，其中每一行中被插入的元素（通过挤入或最终插入到第四行）用粗体表示。因此，4 挤出了 5，5 挤出了 6，6 挤出了 8，而 8 被插入到某一行的末尾。这些粗体元素的位置集合称为插入路径 $I(P\leftarrow 4)$。对于此例，有 $I(P\leftarrow 4)=\{(1,5),(2,4),(3,4),(4,3)\}$。

插入路径有两个技术性质，对于证明RSK算法的性质非常有用。

7.11.2 引理

(a) 当我们将 $k$ 插入到一个SSYT $P$ 中时，插入路径会向左移动。更准确地说，如果 $(r,s),(r+1,t)\in I(P\leftarrow k)$，则 $t\le s$。
(b) 设 $P$ 是一个SSYT，且 $j\le k$。则 $I(P\leftarrow j)$ 严格位于 $I((P\leftarrow j)\leftarrow k)$ 的左侧。更准确地说，如果 $(r,s)\in I(P\leftarrow j)$ 且 $(r,t)\in I((P\leftarrow j)\leftarrow k)$，则 $s<t$。此外，$I((P\leftarrow j)\leftarrow k)$ 不会延伸到 $I(P\leftarrow j)$ 的底部之下。等价地，
$$\#I((P\leftarrow j)\leftarrow k)\le \#I(P\leftarrow j).$$

证明：
(a) 假设 $(r,s)\in I(P\leftarrow k)$。由于 $P$ 的列严格递增，要么 $P_{r+1,s}>P_{rs}$，要么 $P$ 中不存在 $(r+1,s)$ 位置的元素。在第一种情况下，$P_{rs}$ 不能被挤到第 $s$ 列的右侧，否则会违反 $P\leftarrow k$ 的行弱递增性质，因为 $P_{rs}$ 会与 $P_{r+1,s}$ 在同一行中位于其右侧。第二种情况是显然的，因为否则会在第 $r+1$ 行出现空缺。因此，(a) 得证。
(b) 由于一个数只能挤出一个更大的数，因此 $k$ 会被插入到 $P\leftarrow j$ 的第一行中 $j$ 的严格右侧。由于 $P$ 的第一行是弱递增的，$j$ 挤出的元素不会大于 $k$ 挤出的元素。因此，通过归纳法可知，$I(P\leftarrow j)$ 严格位于 $I((P\leftarrow j)\leftarrow k)$ 的左侧。$I(P\leftarrow j)$ 的底部元素 $b$ 是被插入到其行末尾的。根据已证明的内容，如果 $I((P\leftarrow j)\leftarrow k)$ 在这一行有一个元素 $c$，则它位于 $b$ 的右侧。因此，$c$ 被插入到行的末尾，插入过程终止。由此可见，$I((P\leftarrow j)\leftarrow k)$ 永远不会延伸到 $I(P\leftarrow j)$ 的底部之下。

7.11.3 推论

如果 $P$ 是一个SSYT且 $k\ge 1$，则 $P\leftarrow k$ 也是一个SSYT。

证明：显然，$P\leftarrow k$ 的行是弱递增的。现在，一个数 $a$ 只能挤出一个更大的数 $b$。根据引理7.11.2(a)，$b$ 在被挤出时不会向右移动。因此，$b$ 被插入到一个严格小于 $b$ 的数下方，所以 $P\leftarrow k$ 仍然是一个SSYT。

现在设 $A=(a_{ij}{)}_{i,j\ge 1}$ 是一个有限支撑的 $\mathbb{N}$-矩阵。我们可以将 $A$ 视为无限矩阵，或者当 $i>m$ 且 $j>n$ 时 $a_{ij}=0$ 的 $m\times n$ 矩阵。与 $A$ 相关联的是一个广义排列或双线数组 $w_A$，定义为
$$w_A=\left(\begin{array}{ccccc}{i}_1& i_2& i_3& \cdots & i_m\\ j_1& j_2& j_3& \cdots & j_m\end{array}\right),$$
其中 (a) $i_1\le i_2\le \cdots \le i_m$，(b) 如果 $i_r=i_s$ 且 $r\le s$，则 $j_r\le j_s$，以及 © 对于每一对 $(i,j)$，恰好有 $a_{ij}$ 个 $r$ 满足 $(i_r,j_r)=(i,j)$。容易看出，$A$ 唯一确定一个满足 (a)-© 的双线数组 $w_A$，反之亦然。例如，如果
$$A=\left[\begin{array}{ccc}1& 0& 2\\ 0& 2& 0\\ 1& 1& 0\end{array}\right],$$
则对应的双线数组为
$$w_A=\left(\begin{array}{ccccccc}1& 1& 1& 2& 2& 3& \\ 1& 3& 3& 2& 2& 1& 2\end{array}\right).$$

现在，我们与 $A$（或 $w_A$）关联一对形状相同的SSYT $(P,Q)$，定义如下：设 $w_A$ 由 (7.38) 给出。从 $(P(0),Q(0))=(\varnothing ,\varnothing )$ 开始（其中 $\varnothing$ 表示空SSYT）。如果 $t<m$ 且 $(P(t),Q(t))$ 已定义，则定义
(a) $P(t+1)=P(t)\leftarrow j_{t+1}$
(b) $Q(t+1)$ 是通过插入 $i_{t+1}$（保持 $Q(t)$ 的所有部分不变）使得 $P(t+1)$ 和 $Q(t+1)$ 具有相同的形状而得到的。

过程在 $(P(m),Q(m))$ 处结束，我们定义 $(P,Q)=(P(m),Q(m))$。我们将这种对应关系记作 $A\stackrel{\text{RSK}}{\to }(P,Q)$，并称之为RSK算法。我们称 $P$ 为插入表，$Q$ 为记录表。

7.11.4 示例

设 $A$ 和 $w_A$ 由 (7.39) 和 (7.40) 给出。SSYT $(P(1),Q(1)),\dots ,(P(7),Q(7))=(P,Q)$ 如下：

RSK算法的主要结果如下。

7.11.5 定理

RSK算法是有限支撑的 $\mathbb{N}$-矩阵 $A=(a_{ij}{)}_{i,j\ge 1}$ 与形状相同的有序SSYT对 $(P,Q)$ 之间的双射。在这种对应关系中，
$$j\text{ 在 }P\text{ 中出现的次数恰好为 }\sum _i{a}_{ij}\text{ 次}$$
$$i\text{ 在 }Q\text{ 中出现的次数恰好为 }\sum _j{a}_{ij}\text{ 次。}$$
（后两个条件等价于 $\text{type}(P)=\text{col}(A)$，$\text{type}(Q)=\text{row}(A)$。）

证明：根据推论7.11.3，$P$ 是一个SSYT。显然，根据RSK算法的定义，$P$ 和 $Q$ 具有相同的形状，并且 (7.41) 和 (7.42) 成立。因此，我们必须证明以下内容：(a) $Q$ 是一个SSYT，(b) RSK算法是一个双射，即给定 $(P,Q)$，可以唯一恢复 $A$。

为了证明 $Q$ 是一个SSYT，首先注意到 $Q$ 的元素是按弱递增顺序插入的，因此 $Q$ 的行和列是弱递增的。因此，我们必须证明 $Q$ 的列是严格递增的，即 $w_A$ 的顶行中两个相等的元素不会出现在 $Q$ 的同一列中。但如果顶行中 $i_k=i_{k+1}$，则必须有 $j_k\le j_{k+1}$。因此，根据引理7.11.2(b)，$j_{k+1}$ 的插入路径将始终严格位于 $j_k$ 的插入路径的右侧，并且不会延伸到 $j_k$ 的插入路径的底部之下。由此可见，两个插入路径的底部元素位于不同的列中，因此 $Q$ 的列是严格递增的。

上述论证确立了RSK算法的一个重要性质：$Q$ 中的相等元素是严格从左到右插入的。

剩下的任务是证明RSK算法是一个双射。给定 $(P,Q)=(P(m),Q(m))$，设 $Q_{rs}$ 是 $Q$ 中最大元素的最右侧出现位置（其中 $Q_{rs}$ 是 $Q$ 的第 $r$ 行第 $s$ 列的元素）。由于 $Q$ 中的相等元素是从左到右插入的，因此 $Q(m-1)$ 是通过删除 $Q_{rs}$ 得到的 $Q(m)$，并且 $P_{rs}$ 是在将 $j_m$ 插入到 $P(m-1)$ 后被挤入位置的最后一个元素。然而，很容易反转插入过程：$P_{rs}$ 必须是被 $P$ 的第 $r-1$ 行中最右侧小于 $P_{rs}$ 的元素 $P_{r-1,t}$ 挤出的。因此，从 $P$ 中删除 $P_{rs}$，将 $P_{r-1,t}$ 替换为 $P_{rs}$，然后继续将 $P$ 的第 $r-2$ 行中最右侧小于 $P_{r-1,t}$ 的元素替换为 $P_{r-1,t}$，依此类推。最终，某个元素 $j_m$ 会从 $P$ 的第一行中被移除。这样，我们唯一地恢复了 $(i_m,j_m)$ 和 $(P(m-1),Q(m-1))$。通过迭代此过程，我们可以恢复整个双线数组 $w_A$。因此，RSK算法是单射的。

为了证明满射性，我们需要证明将上述过程应用于任意一对形状相同的SSYT $(P,Q)$ 总能得到一个有效的双线数组 $w_A=(i,j)$。显然 $i_1\le i_2\le \cdots \le i_m$，因此我们需要证明如果 $i_k=i_{k+1}$，则 $j_k\le j_{k+1}$。设 $i_k=Q_{rs}$ 和 $i_{k+1}=Q_{uv}$，则 $r\ge u$ 且 $s\le v$。当我们开始对 $P_{rs}$ 进行逆向挤入时，它位于其行 $r$ 的末尾（$m-u$）。因此，当对 $P_{uv}$ 进行逆向挤入时，其“逆向插入路径”在第 $u$ 行严格位于第 $v$ 列的左侧。因此，在第 $u$ 行，$P_{uv}$ 的逆向插入路径严格位于 $P_{rs}$ 的逆向插入路径的左侧。通过简单的归纳论证（本质上是引理7.11.2(b)的“逆向”），$P_{uv}$ 的整个逆向插入路径严格位于 $P_{rs}$ 的逆向插入路径的左侧。特别地，在移除 $i_{k+1}$ 之前，两个元素 $j_k$ 和 $j_{k+1}$ 出现在第一行中，且 $j_k$ 位于 $j_{k+1}$ 的左侧。因此，$j_k\le j_{k+1}$，证毕。

在7.13节中，我们将给出RSK算法的另一种“几何”描述，这对于证明一些显著性质非常有用。这种几何描述仅在矩阵 $A$ 是置换矩阵时定义，即一个 $n\times n$ 的 (0,1)-矩阵，每行和每列恰好有一个1。在这种情况下，双线数组的顶行就是 $12\cdots n$，而底行是 $1,2,\dots ,n$ 的一个排列 $w$，我们可以将其与 $A$ 视为同一。当RSK算法应用于置换矩阵 $A$（或排列 $w\in {\mathfrak{S}}_n$）时，得到的表 $P$ 和 $Q$ 就是标准杨表（形状相同）。反之，如果 $P$ 和 $Q$ 是形状相同的SYT，则满足 $A\stackrel{\text{RSK}}{\to }(P,Q)$ 的矩阵 $A$ 是一个置换矩阵。因此，RSK算法在对称群 ${\mathfrak{S}}_n$ 与形状为 $\lambda ⊢n$ 的SYT对 $(P,Q)$ 之间建立了双射。特别地，如果 $f^{\lambda }$ 表示形状为 $\lambda$ 的SYT的数量，则有基本恒等式
$$\sum _{\lambda ⊢n}(f^{\lambda }{)}^2=n!.(7.43)$$

尽管置换矩阵是有限支撑 $\mathbb{N}$-矩阵的特殊情况，但实际上，任意 $\mathbb{N}$-矩阵 $A$ 的RSK算法可以归结为置换矩阵的情况。具体来说，给定双线数组 $w_A$，假设长度为 $n$，将第一行替换为 $1,2,\dots ,n$，并将第二行替换为其标准化形式，如ECI第57页所定义。为了重申标准化的定义，假设 $w_A$ 的第二行有 $c_i$ 个 $i$。然后将第二行中的1从左到右替换为 $1,2,\dots ,c_1$，接着将2从左到右替换为 $c_1+1,c_1+2,\dots ,c_1+c_2$，依此类推，直到第二行变为 $1,2,\dots ,n$ 的一个排列。将得到的双线数组记为 ${\tilde{w}}_A$。例如，如果
$$A=\left[\begin{array}{ccc}2& 0& 1\\ 0& 1& 1\\ 1& 3& 0\end{array}\right],$$
则
$$w_A=\left(\begin{array}{cccccccc}1& 1& 1& 2& 2& 3& 3& 3\\ 1& 1& 3& 2& 3& 1& 2& 2\end{array}\right),$$
而 $w_A$ 被替换为
$${\tilde{w}}_A=\left(\begin{array}{ccccccccc}1& 2& 3& 4& 5& 6& 7& 8& 9\\ 1& 2& 8& 4& 9& 3& 5& 6& 7\end{array}\right).$$

7.11.6 引理

设 $w_A=\left(\begin{array}{cccc}{i}_1& i_2& \cdots & i_n\\ j_1& j_2& \cdots & j_n\end{array}\right)$ 是一个双线数组，且 ${\tilde{w}}_A=\left(\begin{array}{cccc}1& 2& \cdots & n\\ {\tilde{j}}_1& {\tilde{j}}_2& \cdots & {\tilde{j}}_n\end{array}\right)$。假设 ${\tilde{w}}_A\stackrel{\text{RSK}}{\to }(\tilde{P},\tilde{Q})$。设 $(P,Q)$ 是通过将 $\tilde{Q}$ 中的 $k$ 替换为 $i_k$，并将 $\tilde{P}$ 中的 ${\tilde{j}}_k$ 替换为 $j_k$ 从 $\tilde{P}$ 和 $\tilde{Q}$ 得到的表。则 $w_A\stackrel{\text{RSK}}{\to }(P,Q)$。换句话说，操作 $w_A\mapsto {\tilde{w}}_A$ 与RSK算法“交换”。

证明：假设在RSK算法的某个阶段，当数字 $j$ 被插入到某一行时，它位于该行的第 $k$ 个位置。如果将这个数字 $j$ 替换为一个更大的数字 $j+ϵ$，且小于该行中大于 $j$ 的任何元素，则 $j+ϵ$ 也会被插入到第 $k$ 个位置。由此可见，对于元素 $j_1,j_2,\dots ,j_n$ 的插入过程完全模仿了对于 ${\tilde{j}}_1,{\tilde{j}}_2,\dots ,{\tilde{j}}_n$ 的插入过程，证毕。