第12章 因子投资中的机器学习

12.1 量化金融中的人工智能

随着机器学习和人工智能在诸多领域取得重大突破，尤其是以GPT为代表的生成式AI模型展现出令人惊叹的潜力，因子投资的学术界与业界都渴望借助机器学习算法的强大能力来提升因子投资策略。越来越多充满热情的实践者开始探索AI算法的应用，但必须清醒认识到：当前AI工具在基础自动化与初级分析方面虽已取得长足进步，但试图让AI直接做出投资决策或真正理解金融市场运行机制的努力尚未取得显著成功。

• 卷积神经网络（CNN）和循环神经网络（RNN）是两种对金融市场建模分析做出重要贡献的深度学习架构。
  • CNN专为处理网格状数据（如图像或时间序列）设计，通过卷积运算捕捉局部特征。
    • 其卷积层对输入数据的局部区域施加滤波器，提取空间或时间模式，从而自动从数据中学习从低级到高级的层次化特征表达。
    • 金融领域，CNN已被应用于股价预测、异常检测和情感分析等任务，能够从历史价格数据、新闻文本或社交媒体情绪中提取有效模式，提升预测准确性并识别市场趋势。
  • RNN则擅长捕捉序列依赖性，特别适合处理具有时序关联的数据。
    • 通过内部记忆机制，RNN能保留历史输入信息并用于逐步预测，使其在股市预测、组合优化和信用风险评估等任务中表现卓越。
    • STM和GRU等RNN变体通过门控机制有效解决了长期依赖问题。利用金融数据的时间动态特性，RNN能建模复杂关系并揭示隐藏模式，从而提升金融预测与决策的准确性。
• CNN与RNN的混合架构（如ConvLSTM）在金融建模中展现出独特优势——先用CNN提取局部特征，再通过LSTM层捕捉时序依赖。该方法在金融时间序列预测、欺诈检测和算法交易等领域成效显著。
• 通过CNN和RNN，金融模型能够自动从复杂数据中学习有效特征，建模空间、时间和序列关系，提供更精准的预测与洞察。
• 但需注意，这些架构的成功应用高度依赖数据质量、预处理技术以及稳健的模型训练验证流程。

从本书的核心关切——也是因子投资必须考量的数据分布变化问题——我们就能理解为何将金融决策权交给AI是极具挑战的任务。当前取得辉煌成功的算法多属归纳法，即从数据相关性中推导规律。AI在图像和文本的识别、理解与生成方面固然取得惊人进展，但必须认识到：未来数据分布可能发生变化，这将瓦解对历史数据分布观测的依赖。读者可参阅本书$第10章$了解分布不确定性何时出现，进而理解机器学习的局限性。

数学上，这暗示数据生成过程具有时变性。金融研究中常见现象包括：某些模式或因子随时间推移失效；在发达股市有效的因子在新兴市场呈现相反效应（如中美股市中的动量因子差异）。因此，算法智能生成的核心难题或许在于应对数据生成过程的分布变化。

此外，我们接触的数据往往存在偏差且不能代表整体样本空间。例如，分析医院患者数据可能得出"就诊者死亡率高于普通人群"的悖论，但这显然不能推导出"就医导致病情恶化"的结论——因为只有不适者才会就医。要分析就医效果，还需获取不适却未就医人群的健康数据。 回到因子投资，我们使用的历史数据仅是人类历史的微小片段。以近年美股由科技巨头驱动持续上涨为例，这种市场结构可能导致训练数据识别的因子偏向大市值股票，误将市值作为有效预测变量。但是，长期视角显示，小市值股票往往能获得更高超额收益（即著名的小市值因子）。

数据生成过程的分布变化可能性和观测数据的偏差，使得未经改造的机器学习算法直接在金融领域应用难以成功。中国古代兵家智慧有云，“为将者未虑胜先虑败”，深刻揭示了认识并准备应对失败可能性的重要性。

我们不惜篇幅讨论这些核心问题，因为理解机器学习应用于投资的困难，是开发新技术克服或缓解这些挑战、或寻找折中方案绕开它们的第一步。这些问题可能将长期作为重要学术难题存在，其启示在于：运用先进AI算法进行因子投资时，不应抛弃因子研究的逻辑分析——事实上因子背后的逻辑更需要被重视。因子仅是股票属性的量化表征，理解这些表征背后的原理才至关重要。事实上，鉴于金融数据存在诸多机器学习模型假设的违背、低信噪比和非平稳性（Nagel 2021），用经济理论指导机器学习算法正是其成功的关键。

本章将从机器学习视角全面阐释因子投资的现状与未来，为读者提供前瞻性思考。具体安排如下：

12.2节 讨论机器学习如何应用于因子投资实践全流程；
12.3节 深入解析机器学习在实证资产定价和因子投资应用的最新进展；
12.4节 聚焦因子发现这一关键问题与机器学习的可能角色；
12.5节 对比因子投资中的机器学习与计量经济学方法；
12.6节 总结全文。

12.2 量化因子投资的AI化组件：解剖学视角

本节首先采用分析视角，解构量化因子投资全流程的主要阶段，思考每个阶段如何引入机器学习算法。按此思路，我们逐步分析各环节，初步识别算法能显著提升投资实践的领域。

12.2.1 数据源拓展与预处理

除传统结构化金融数据外，蕴含丰富市场与个股信息的非结构化数据亟待挖掘。AI可优化信息收集的全面性与及时性，基于GPT的工具能提供重要助力。

AI算法还能实时监控数据质量与异常。在非结构化数据（如新闻情绪或公司知识图谱）的信息提取中（Bybee, Kelly and Su 2023; Bybee et al. forthcoming），AI擅长从文本与图像中提取具有股票收益预测信息的量化指标。

此外，数据预处理中的智能化数据库工程（如数据更新、校验、缺失值填充（Freyberger et al. 2021; Bryzgalov et al. 2022）、向量化查询、负载均衡存储与分布式计算）也是AI算法的用武之地。

12.2.2 因子研究

因子研究的核心在于因子发现。因子逻辑的自动化挖掘与提取是极具前景的AI应用方向，但需要大量工程与学术支持以实现进一步发展。本章12.4节将深入探讨。

12.2.3 因子模型

为解释资产或组合横截面预期收益，各类定价模型被提出、讨论，金融学术界逐渐形成基于机器学习的研究范式（12.3节将详述）。

当识别出大量预测因子后，如何有效整合形成可交易信号成为关键。

高维度和因子间相关性带来重大挑战，这为机器学习算法提供了广阔应用空间。

此外，复杂因子组合模型中可纳入市场环境变量，希望通过复杂模型的非线性拟合能力增强现有线性因子。当然，需警惕模型复杂度提升导致的过拟合风险，通过$必要正则化$等技术进行防控。

12.2.4 风险分析与组合优化

生成收益预测信号后，组合风险分析是核心环节。

理解收益源于特定风险承担，风险控制优化的核心目标是在预设风险约束下最大化收益。

新兴研究方向包括：建立强化学习模型与模拟环境，基于资产定价模型设定风险暴露水平，定义动作空间（股票买卖），训练强化代理根据预测信号与定义的风险控制惩罚进行优化。

12.2.5 交易执行与监控

量化研究分析后的最终环节是实际交易执行。该过程存在大量优化机会，如前文提到的流动性对交易执行的影响。

反映短期股价走势的高频数据可用于开发交易算法。由于优化交易执行算法的数据频率更高，数据分布变化程度相对较小，可采用复杂算法解析市场微观结构与短期供需动态。

12.3 机器学习与资产定价

自Gu, Kelly和Xiu(2020)将机器学习方法正式引入实证资产定价研究以来，过去几年学术界大量学者应用各类机器学习模型（线性和非线性）进行股票收益预测，并识别应纳入定价模型或随机贴现因子(SDF, stochastic discount factor)的因子。Kelly和Xiu(2023)提供了精彩综述。

这一转变主要源于因子数量的指数级增长及因子与资产收益间复杂关系——这是大数据与机器学习时代的典型特征。这些发展对基于计量方法的传统实证研究提出了重大挑战。虽然计量技术仍是分析简单线性关系和参数判定的有力工具，但在处理高维预测问题时并非首选方案（12.5节将详细对比机器学习与计量经济学）。已在自然语言处理和图像识别等领域验证为有效的机器学习算法，自然成为了解决此类复杂问题的选择。

因此，学术研究明显从提出简约而特殊的多因子模型（以减少市场异象为目标），转向日益突出的机器学习方法。这催生了围绕多因子模型和随机贴现因子(SDF)的新研究范式，研究导向悄然从"程序性"开发转向"实证性"驱动。采用机器学习算法进行资产定价的论文大量发表于顶级期刊是最有力的证据。同时，各类机器学习算法已进入因子投资的行业实践，尤其在因子发现与聚合方面。

回望学术研究，深入审视这些实证工作可发现，它们在理论阐述与实证结果方面存在大量共性。精读这些文献能极大提升我们对机器学习算法应用于实证资产定价和因子投资的理解。本节旨在为读者客观呈现该领域现状，通过五组事实与虚构的讨论，厘清机器学习与资产定价的真相与误解。

12.3.1 虚构1：数据会"自己说话"

第一个虚构观点认为：只需将数据盲目输入复杂机器学习算法，单纯期待数据"自己说话"。

金融数据固有的低信噪比和非平稳性，足以打破"对金融数据直接套用现成机器学习 就能获得有意义洞见"的天真幻想。
在资产定价领域，参数先验分布、协变量缩放、正则化惩罚和调优标准选择等诸多方面都会显著影响结果。

• Nagel(2021)的示例虽简单但有效地阐明了上述考量：假设用过去120天收益及其平方、立方值作为协变量，预测次日收益。
• 表12.1总结了不同设置下的预测结果，其中：
  • Method列表示采用的正则化方法（OLS表示无正则化）
  • Scaling列显示协变量标准化方式
    • Equal表示所有协变量标准化为均值0、标准差1
    • Unequal表示标准化后标准差不同
  • CV Criterion列表示交叉验证采用的指标（如R平方或组合预期收益）。
  • 表中OLS指普通最小二乘法，IS指样本内，CV指交叉验证。

Method	Scaling	CV Criterion	IS $R^2$	CV $R^2$	CV Portfolio Sharpe Ratio
OLS	Equal	N/A	5.22%	-1.18%	0.35
Ridge	Equal	$R^2$	2.63%	0.84%	0.30
Ridge	Unequal	$R^2$	2.69%	1.18%	0.37
Ridge	Unequal	$E[r_p]$	1.75%	0.89%	0.35
Lasso	Unequal	$R^2$	3.55%	0.84%	0.36

表12.1 收益预测示例 数据来源：摘编自Nagel(2021)表3.2

• 实证结果显示，模型设定对结果影响显著。
• 但面对海量选项时，穷举所有排列组合既不现实也不明智，关键在于有效利用金融理论衍生的先验知识。
  • 例如：
    • 若假设模型非稀疏，可能选择岭回归而非Lasso；
    • 若认为协变量对收益预测重要性不同，可能选择非等比例缩放；
    • 若从金融理论核心出发，可能选择优化夏普比率（或最小化定价误差）而非传统R平方。
  • 这些决策本质上都源于资产定价理论。

12.3.2 事实1：在资产定价框架内应用机器学习

与虚构1相反，第一个事实指出：我们应在资产定价理论框架内运用大数据与机器学习算法。

实证资产定价领域从CAPM到APT/ICAPM，再到庞杂的因子动物园，无疑通过大量实证挑战推动了学科发展。尽管范式几经变迁，但研究核心始终围绕资产定价理论展开。例如Bryzgalova, Pelger和Zhu（即将发表）与Chen, Pelger和Zhu(2023)这两篇近期重要论文，前者采用决策树，后者运用生成对抗网络(GAN)，但都将SDF框架作为应用不同算法于资产定价的基础。

类似地，Kelly, Pruitt和Su(2019)的工具化主成分分析(IPCA)与Gu, Kelly和Xiu(2021)的自编码器模型，都采用潜在因子模型，将因子暴露(β)建模为协变量（如公司特征与宏观经济变量）的函数。二者区别在于，前者使用线性模型，后者选择非线性模型。且由于协变量具有时变性，这两种方法本质上都属于条件定价模型。

实证上，这些研究的共同点是，使用远超传统研究数量的协变量，并通过组合样本外表现，从而验证方法的有效性。尽管这些论文尝试不同机器学习算法，但鉴于SDF与多因子模型的等价性，其方法可在统一框架下检视理解，展现了先进机器学习技术与基础资产定价理论的融合。

12.3.3 虚构2：机器学习模型忽视可解释性

第二个虚构观点认为：机器学习模型是黑箱，学术研究忽视可解释性。

可解释性是传统多因子模型或异象研究的精髓。例如Fama和French(2015)五因子模型基于股利贴现模型，Hou, Xue和Zhang(2015)的$q因子模型$则立足$q理论$。异象论文也提供解释，将其归类为风险补偿或错误定价。当研究目标转向通过复杂模型更准确预测资产收益时，似乎产生"弱化可解释性重视程度"的误解，但事实并非如此。

对线性模型（如Kozak, Nagel和Santosh(2018,2020)的主成分分析和Kelly, Pruitt和Su(2019)的IPCA），可解释性相当直观。
前者发现：对规模和价值构建的25个组合进行PCA得到的前两个主成分(PC)，完美对应小减大（规模）和高减低（价值）因子。
后者虽数学表达复杂，但其底层直觉本质上是通过横截面回归构建管理组合的线性组合。
因此对线性模型，其可解释性深深植根于人们熟悉的回归与组合排序。

对非线性模型，其可解释性虽不如线性模型直观，但学术研究仍高度重视（事实2将讨论）。探究模型预测背后的"原因"与"机制"始终是基本追求，确保即使最复杂的模型也致力于实现一定程度的透明性与清晰解释，符合学术研究不仅追求预测准确性，也追求可理解洞察的目标。

12.3.4 事实2：机器学习揭示关键预测变量

作为对虚构2的回应，第二个事实指出：机器学习揭示了与大量实证资产定价发现相吻合的最重要预测变量。

Gu, Kelly和Xiu(2020)通过排列重要性识别对解释预期收益最关键协变量，发现：

1. 最重要协变量与既往实证发现一致，主要分为动量/反转、流动性相关、风险相关（如 idiosyncratic volatility）和基本面四大类（注意，这些都是本书论述的重要因子）；
2. 不同机器学习模型的最重要协变量高度重叠。

此外，Chen, Pelger和Zhu(2023)通过计算SDF权重对协变量的偏导数评估模型可解释性，发现所有协变量中影响力最大者涉及交易摩擦、价值、无形资产、盈利能力、投资和历史收益等方面。

另一值得关注的是Kozak(2019)，其巧妙运用核技巧，将协变量映射到高维空间而不增加计算复杂度，再对这些转换后协变量进行PCA。非线性核的使用模糊了转换后协变量的性质，但通过将构建的SDF映射回原始协变量的管理组合，仍可识别最重要的解释变量。

最后，如Avramov, Cheng和Metzker(2023)所示，通过观察不同协变量下选定股票的共性特征，也能推断某些变量的重要性。

这些方法印证了机器学习衍生的预测因子与大量实证资产定价结果的一致性，在数据驱动的金融创新景观中确认了基础原则的连续性。

12.3.5 虚构3：复杂模型必然导致糟糕样本外表现

• 初看虚构3，似乎合理：复杂模型容易样本内过拟合，导致样本外预测误差大幅增加。
• 该观点认为随着模型复杂度提升，其捕捉和复制样本内数据细微特征的能力增强，可能以牺牲对未见数据的泛化能力为代价。
• 这一论述基于对模型复杂度及其与欠拟合、过拟合关系的传统理解。
  • 低复杂度时，模型倾向欠拟合，表现为低方差、高偏差；
  • 复杂度增加时，偏差降低但方差增加，导致过拟合。
  • 这种相互作用被称为偏差-方差权衡，暗示存在使样本外误差（即测试风险）最小化的最优超参数集。
  • 参见图12.1左侧展示这一经典U型关系。

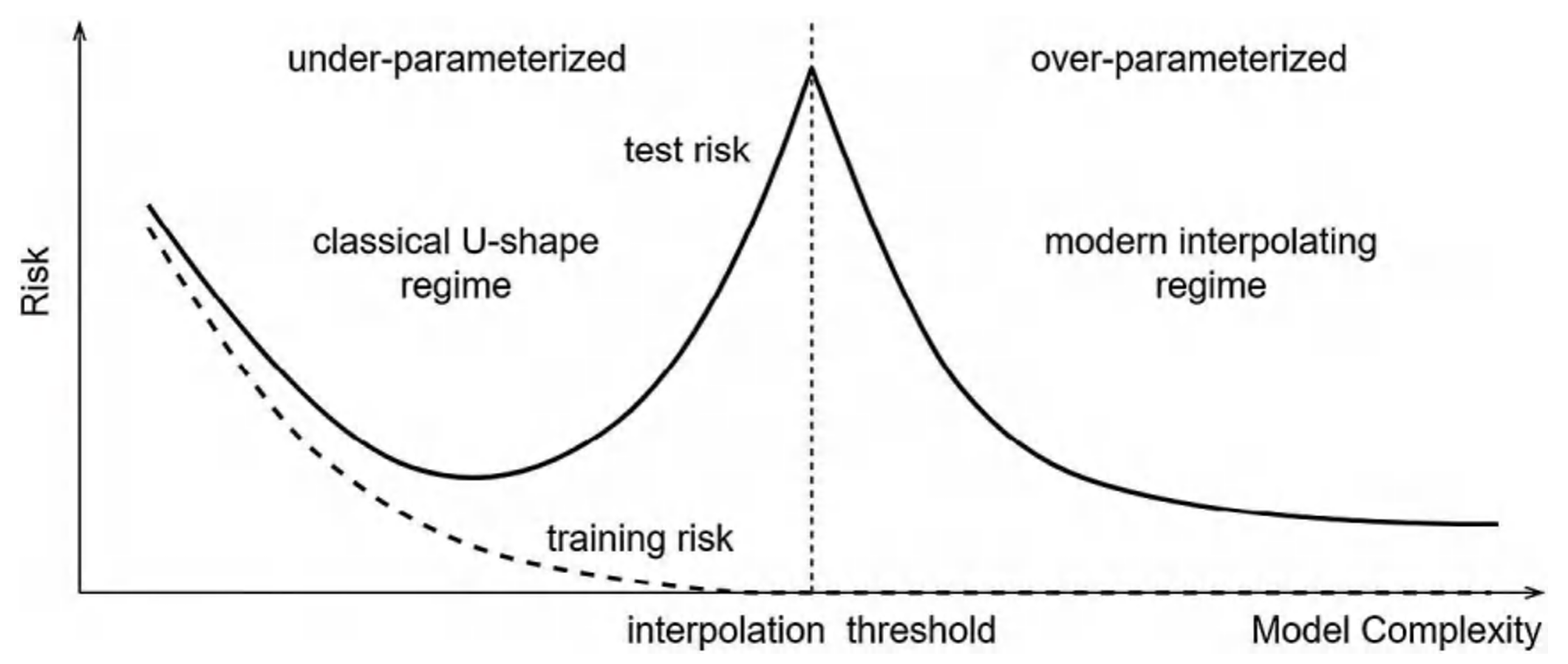
图12.1 风险 vs. 模型复杂度

• 这种权衡也可从另一视角理解：
  • 简单模型善于避免过拟合，但可能无法准确近似真实世界；
  • 复杂模型或许更接近现实世界现象，但确实更容易过拟合。
• 因此偏差-方差权衡也可解读为近似-过拟合权衡。
• 机器学习与统计建模的传统智慧由此认为：参数过多（即参数量远超训练数据量）会导致过拟合，因为模型会学习训练数据中的噪声而非底层模式。
• 因此，通常建议模型参数量应远小于训练数据量。

但在深度学习领域，这一传统智慧并不总成立。尽管参数量常超过训练数据量，但深度学习模型被发现对未见数据具有良好的泛化能力。这一现象常被称为**"双下降"曲线**（Loog等2020），显示当参数量超过训练数据规模后，模型测试性能可能再次提升。

该现象原因仍是研究热点。有理论认为，深度学习模型结构和训练算法的非凸优化特性具有隐式正则化效果；也有观点认为，过参数化模型能表达更广阔函数空间，增加找到同时拟合训练数据且泛化良好模型的机会。尽管尚无定论，过参数化深度学习模型的有效性已是实证事实。

12.3.6 事实3：适当正则化下模型复杂度收益超越统计代价

机器学习理论发展有力反驳了虚构3，指出复杂模型能更准确逼近真实数据生成过程(DGP, data generating process)。只要施加足够正则化，模型复杂度带来的优势可能超越过参数化的统计代价。

近年来机器学习领域最激动人心的发现正是双下降现象——样本外误差与模型复杂度呈现非单调关系。如Belkin等(2019)指出：当模型复杂度突破样本量限制时（传统认为应避免的区域），样本外总误差非但没有"爆炸"，反而随复杂度增加开始单调下降（如图12.1右侧所示）。这种在插值阈值两侧均呈现误差单调下降的现象被命名为双下降。

该现象直觉在于：当协变量数量超过样本量时，样本内解不再唯一。
最优解可理解为参数方差最小的解。
随着模型复杂度提升，最优解方差降低。
此外，需注意所有模型都是真实DGP的某种误设。当存在模型误设时，可以证明在变量数超过样本量的特定范围内，偏差也可能随复杂度增加而降低。综合效应导致测试风险下降。
对双下降理论基础感兴趣的读者可参阅Hastie等(2022)的详细讨论。

在实证资产定价中，Kelly、Malamud和Zhou(2024)将这一概念应用于美股市场择时，观察到类似双下降现象：当协变量数量远超样本量时，样本外夏普比率得到改善。Didisheim等(2023)进一步将该思想拓展至横截面，研究因子定价模型中的复杂度问题。

虽然机器学习理论最新进展令人振奋，但需注意关于模型复杂度与样本外表现的讨论仍处起步阶段。正则化在此过程中至关重要，该领域有待更多研究。

12.3.7 虚构4：非线性模型可轻易实现夏普比率翻倍

虚构4指错误认为非线性模型可轻易实现夏普比率翻倍。但是，让我们先检视一组看似支持该观点的有力实证结果。

Baba-Yara、Boyer和Davis(2021)复制了近年来一些主要机器学习资产定价模型，并与传统因子模型比较性能。表12.2汇总了部分代表性结果。

机器学习模型	机器学习模型	传统因子模型	传统因子模型
模型	OOS夏普	模型	OOS夏普
BPZ随机森林	2.19	FF3	0.45
Davis神经网络	3.21	FF5+MOM	1.03
KNS PCA	3.21	Hou-Xue-Zhang	1.10
KPS IPCA	3.39	Stambaugh-Yuan	0.61

表12.2 机器学习与传统因子模型比较 数据来源：摘编自Baba-Yara等(2021)

结果生动地显示了：相比传统因子模型，机器学习模型实现的夏普比率确实达到传统模型两倍甚至三倍。但需牢记，传统模型是稀疏的，构建因子时使用的协变量少得多。这种比较本质上不公平。（我们将在事实4重新审视这些结果。）

另一方面，细看可发现上述结果中PCA和IPCA模型（均为非条件线性模型）的夏普比率实际上高于采用随机森林和神经网络等非线性模型的成果。这似乎表明至少在引用的实证结果中，非线性模型未必优于线性模型。

12.3.8 事实4：非线性模型提供边际增量贡献

毫无疑问，协变量与资产收益间存在非线性关系。但在现阶段，非线性模型更可能提供解释横截面的边际增量贡献。

如Nagel(2021)和大量近期实证资产定价研究所示，变量间交互作用在这些非线性关系中至关重要。对传统线性回归模型，随着变量增加，考虑所有协变量对的交互项变得不切实际。这为擅长处理非线性关系的机器学习模型提供了机会。

但对非线性关系带来的收益预测增量贡献需保持现实预期。Chen、Pelger和Zhu(2023)的实证发现表明：他们的GAN在构建SDF时能捕捉协变量间交互作用，但也强调单个协变量对SDF的影响几乎呈线性。

现在重新审视虚构4提到的Baba-Yara等(2021)研究。他们早期版本论文的实证期间为1990-2020年，而最新版本却奇怪地缩短为1990-2016年。更令人困惑的是作者解释称比较的传统模型之一Stambaugh-Yuan模型数据仅更新至2016年。但若早期版本能研究至2020年，为何新版本要回退至更早截止日期？真实动机不得而知。

机器学习模型	OOS夏普(2020)	传统因子模型	OOS夏普(2020)
BPZ随机森林	0.86(2.19)	FF3	0.61(0.45)
Davis神经网络	2.39(3.21)	FF5+MOM	1.17(1.03)
KNS PCA	2.77(3.21)	Hou-Xue-Zhang	1.81(1.10)
KPS IPCA	3.21(3.39)	Stambaugh-Yuan	1.40(0.61)

表12.3 机器学习与传统因子模型比较(II) 数据来源：摘编自Baba-Yara等(2021)

在这个缩短的实证期间，结果汇总于表12.3（括号内为截至2020年的结果，供比较）。耐人寻味的是：当实证截止期设为2016年，四个机器学习模型均出现不同程度恶化，而四个传统模型全部改善。

聚焦机器学习模型，这些比较显示不同实证期间结果存在显著波动。同时，尽管这些研究采用滚动或扩展窗口进行训练验证后才预测下一年样本外收益，但关于调参过程及不同超参数下模型稳健性的讨论极少（如果有的话）。这方面应用机器学习于资产定价的研究生态远未成熟，亟需领域领导者建立公认研究规范。

12.3.9 虚构5：机器学习模型可轻松付诸实践

最后一个虚构观点认为，机器学习模型可轻松在实践中应用。虽然机器学习模型在资产定价学术研究中取得了鼓舞人心的成果，但并不意味着能轻松在实践中获得扣除所有成本后的显著超额净收益。

这方面最关键实证发现之一是机器学习模型构建组合的高换手率。Avramov、Cheng和Metzker(2023)复制了文献中多个领先机器学习模型，包括Gu、Kelly和Xiu(2020)的神经网络、Chen、Pelger和Zhu(2023)的GAN、Kelly、Pruitt和Su(2019)的IPCA，以及Gu、Kelly和Xiu(2021)的条件自编码器。这些模型的平均月换手率如表12.4所示。
作为参照，传统低频风格因子（如规模和价值）通常月均换手率低于10%（即0.1）。
通过交易成本估算，Avramov等(2023)指出在这种高换手下，投资者难以通过机器学习模型获得额外超额收益（尽管不排除部分成熟投资者能成功改造这些模型在高换手下实现超额收益）。

模型	月均换手率
Gu、Kelly和Xiu(2020)	0.976
Chen、Pelger和Zhu(2023)	1.664
Kelly、Pruitt和Su(2019)	1.186
Gu、Kelly和Xiu(2021)	1.565

表12.4 机器学习模型换手率

为解决交易成本挑战，Jensen等(2022)提出"可实施有效前沿"概念，通过考虑成本后收益直接评估策略。该方法将包含交易成本的组合优化问题整合到机器学习框架，取得良好效果。这一进展凸显在投资策略中部署机器学习模型时考虑交易成本等实际约束的必要性，揭示了学术成功与实际应用间的微妙差距。

12.3.10 事实5：对部分机构投资者价值有限

与虚构5相反，事实是：先进机器学习模型揭示的预测能力部分集中于高套利成本和高交易成本股票，因此对部分机构投资者的价值有限。

实证发现表明，许多异象的超额收益主要来源于空头端(Avramov等2013)或极小市值股票(Novy-Marx和Velikov2016)。类似地，机器学习模型展现出从高套利成本和高交易成本股票中提取预测能力的长处，这削弱了其实用性。

以Avramov、Cheng和Metzker(2023)的实证结果为例，除全样本外还检验三个子样本：剔除极小市值股票、无信用评级公司和财务困境企业。结果（表12.5，括号内为t统计量）显示主流机器学习模型（IPCA除外）在这些子样本中相比全样本表现显著下降。此外，部分机器学习模型相对于FF5+MOM基准的alpha在某些子样本中不再显著。

模型	全样本	剔除极小市值	剔除无信用评级	剔除财务困境
面板A：绝对收益(%)
Gu、Kelly和Xiu(2020)	1.56	1.05	1.02	0.72
	(4.53)	(3.24)	(3.18)	(2.49)
Chen、Peiger和Zhu(2023)	2.13	1.08	0.82	0.92
	(6.37)	(4.06)	(2.83)	(2.91)
Kelly、Pruitt和Su(2019)	0.95	0.91	0.89	0.73
	(5.62)	(5.57)	(5.08)	(4.08)
Gu、Kelly和Xiu(2021)	1.16	1.11	0.87	0.67
	(4.17)	(4.22)	(2.97)	(2.22)
面板B：相对FF5+MOM的alpha(%)
Gu、Kelly和Xiu(2020)	0.92	0.31	0.43	0.20
	(4.08)	(1.51)	(2.05)	(0.92)
Chen、Peiger和Zhu(2023)	1.87	0.55	0.42	0.57
	(4.86)	(2.23)	(1.46)	(1.82)
Kelly、Pruitt和Su(2019)	0.62	0.61	0.61	0.43
	(3.31)	(3.71)	(3.38)	(2.37)
Gu、Kelly和Xiu(2021)	0.75	0.39	0.19	0.05
	(3.01)	(2.03)	(0.79)	(0.20)

表12.5 不同样本中模型表现 数据来源：摘编自Avramov等(2023)

例如，GAN模型在剔除极小市值股票子样本中的月收益相比全样本下降超50%。
在检验的四个模型中，除IPCA（线性模型）外，其余非线性模型中仅IPCA在全样本和各子样本中表现稳健。

值得注意的是，子样本结果仍使用全样本训练模型得出，这可能引发部分读者担忧。
对此，Avramov等(2023)进一步使用子样本训练并进行样本外预测，发现结果无实质变化，甚至某些子样本中样本外表现下降。
换言之，约束模型从目标样本学习的意图，反而因样本量减少导致样本外表现更差。

这些结果暗示：成功改造非线性模型使其聚焦于低套利成本和低交易成本股票，将是机器学习模型在资产定价中实际应用的关键前提。

12.4 自动化因子发现

随着人工智能算法持续进步，利用算法进行因子发现以替代人工操作的兴趣日益增长。本节探讨这一方法的可行性。

12.4.1 端到端因子拟合

可能首先想到（虽非我们最推荐）的是，直接采用深度学习模型进行端到端因子训练。深度学习模型具有强大的拟合能力，梯度可提供快速搜索解的优化方向。此方法中，直接预测股票收益可作为目标，但这常导致模型输出过度相似和过拟合。

更有效的方法可能是基于金融逻辑设定众多中间目标。该方法通过多样化目标和为每个目标单独建模，可增强模型输出多样性、并允许调整预测目标。*例如，模型可预测股票基础属性（如换手率、波动率、股票间相关性或收益分布），或更复杂的预测如每股收益、投资者情绪或财报提前发布概率等。*预测目标应利用人们对金融市场的理解，部分目标可根据数据可获得性由模型预测。

此外，可采用无监督学习方法提取股票收益的潜在信息，如使用编码器-解码器架构。该方法将因子视为股票潜在信息的量化描述，但缺点在于缺乏对模型预测的透明理解和潜在错误的识别。尽管可采用必要技术防控过拟合，但其仍是固有风险。

12.4.2 自动化符号化因子

除直接模型拟合外，对量化因子研究者更复杂但可靠的方法是挖掘数据-算子组合。本书讨论的许多金融逻辑因子可分解为多个子逻辑，每个子逻辑通过算子应用于一个或多个变量。这种逐步逻辑链可表达复杂因子。图12.2通过示例说明这一概念。

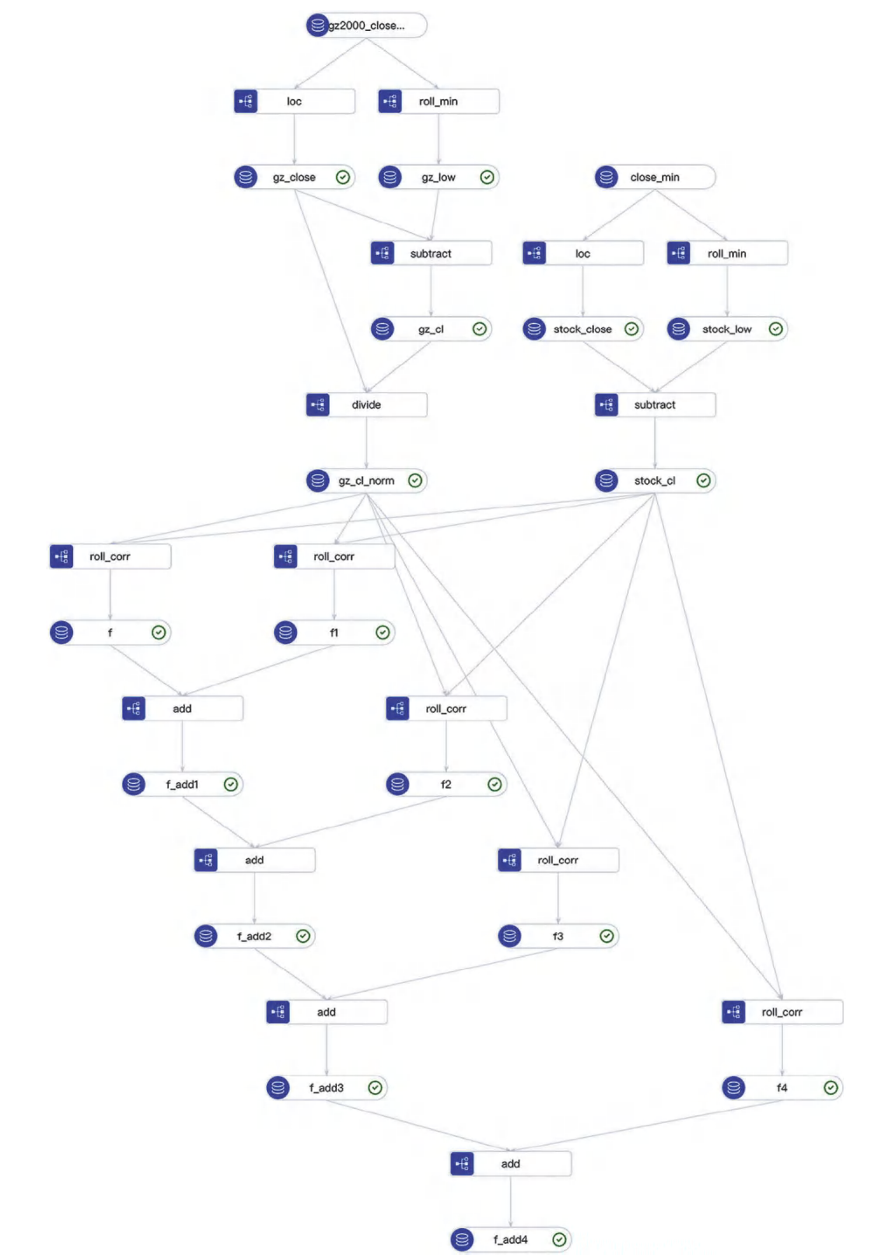
图12.2 自动化符号化因子

实现因子自动搜索需要以下组件：

1. 操作数空间：用于因子挖掘的元因子，如价格、成交量、行业分类、限价订单簿特征、分析师/财报统计数据、投资者情绪信号等。
   • 该空间应丰富包含反映股票内在属性的变量（如前面章节讨论）。
   • 理论上更广阔、更高维的操作数空间能提供更有意义逻辑发现的可能性。
2. 操作符空间：用于处理因子的操作符，如平方根、对数、排序、均值、分位数等，以及后处理操作符（如离群值裁剪的缩尾处理和数据标准化）。
   • 与操作数空间类似，多样化的操作符集合能增强搜索能力。
3. 搜索算法：旨在发现有效因子，方法包括随机组合的蒙特卡洛(MC)算法，更复杂的马尔可夫链蒙特卡洛(MCMC)和遗传编程等。
   • 最新研究探索使用生成模型和LangChain基于金融逻辑提出操作数和操作符组合。
4. 评估：简单标准包括信息系数(IC)、年化收益和夏普比率。
   • 为避免高相关性因子冗余，可采用数据驱动的解释算法增强搜索因子的逻辑连贯性。
5. 迭代：研究者需持续理解生成结果，识别系统缺陷，并根据结果调整搜索算法或扩展操作数和操作符。
   • 迭代改进对建立功能性因子发现系统至关重要。

Cheng和Tang(2024)研究了GPT-4生成因子的能力。
研究表明：ChatGPT利用GPT-4能力生成的因子在收益和风险方面表现优异，展现出可观的夏普比率和超越传统因子模型的年化收益轨迹。通过模型平均范式，ChatGPT生成的35个因子集合显示出卓越的多空年化收益和显著夏普比率，优于传统数据挖掘技术。
GPT-4因子生成过程的突出优势是时间效率——不同于依赖大量数据挖掘的传统方法，GPT-4基于知识的推理允许无需大量金融数据即可快速生成因子。重要的是ChatGPT提供基于经济理论的生成因子全面解析，这区别于纯数据挖掘方法，增强了因子的可解释性和稳健性。
该研究凸显了ChatGPT等大型语言模型(LLM)在因子生成中日益增长的相关性。

金融市场收益预测传统依赖词袋法，无法捕捉文本句法和语义。而自然语言处理领域最先进的LLM提供的语境化表征能更全面理解新闻文本。Chen等(2024)探索使用16个国家股票市场和13种语言新闻数据，研究语境化表征在收益预测中的功效。这些表征捕获文本的语境信息和细微差别，克服了词袋法的局限（尤其涉及否定词的情况）。研究发现，新闻信息以非有效延迟方式纳入股价，但利用实时新闻提醒的交易策略能利用新闻诱导的收益可预测性，产生了更高夏普比率。

关于因子可解释性，Guo等(2023)的方法包括：

1. 股票解释：提供股票与其他股票关系、股票相似性、领先-滞后效应和行业趋势的洞见，有助于更好理解其行为及在分析和预测中相比传统方法的潜在优势。但确定适当相似性指标、识别领先-滞后效应及评估行业贡献和特征交互等方面存在挑战。
2. 时间解释：提供特定时点市场特征和异常的洞察，包括极端市场状况、日历效应、风格转换和突发事件影响。通过分解收益、识别重要日历因子、检测风格转换和分析事件影响，投资者可调整策略以应对市场动态。
3. 因子解释：分析股票对不同因子随时间变化的敏感性，识别因子间交互效应。因子可根据数据源、金融特征和时间尺度等多方面分类，计算其对组合收益的贡献。通过特征交叉技术揭示因子交互作用，使用层次聚类等技术创建因子相似性的层次化描述。

这种利用AI算法进行因子研究的多维方法，强调了将先进技术整合到因子投资的复杂性和潜力，凸显了在这一演进领域持续探索和完善的重要性。

12.5 机器学习 vs. 计量经济学

毫无疑问，机器学习已逐渐取代计量经济学方法，成为当代资产定价和因子投资的主导工具。但在结束本章前，从统计建模视角检视这两种方法的差异颇具启发性（Mullainathan和Spiess 2017, Athey和Imbens 2019）。这种比较能加深我们对方法论的理解，从而为手头问题选择合适技术。

12.5.1 两种文化

• Leo Breiman在其开创性论文《统计建模：两种文化》（Breiman 2001）中深入探讨统计建模的两种主流文化。
  • 第一种是数据建模文化，假设数据生成过程基于某个随机模型，并据此进行统计推断。
    • 其主要目标是理解数据结构和内部关系，即传统数据建模文化的本质在于通过一系列假设和理论框架理解数据生成机制。
    • 该文化中广为人知的计量经济学方法，依赖建立显式模型解释变量间关系，通常假设线性关系和误差正态分布。
    • 该方法主要目标是参数估计而非预测，旨在阐明变量间因果关系。
      • 当数据符合模型假设时，该方法可提供强有力的因果解释。时间序列回归或Fama和MacBeth(1973)横截面回归等实证研究方法都属于这一文化。
      • 但当预测精度优先于无偏参数估计时，会发生什么？
  • 第二种是算法建模文化，优先考虑预测精度而非模型可解释性。
    • 该方法不对数据生成过程做严格结构假设，而是采用数据驱动方法直接从数据中学习。
    • 机器学习模型是这一文化的典型代表。其灵活性使其能处理复杂、非线性和高维数据，无需预设数据结构。
      • 但机器学习模型常因"黑箱"特性受到批评。
    • 该文化中不对数据结构做任何假设，而是选择一类模型（如神经网络）并根据给定损失函数从数据中学习模型参数。
    • 机器学习建模核心是优化模型样本外泛化性能，或等价于最小化泛化误差，由此引入正则化这一关键概念。
    • 相比计量经济学，机器学习方法无需明确定义模型形式即可逼近非线性、高维和复杂函数关系，使其自然适合解决当代实证资产定价挑战。
• 通过这两种文化视角观察计量经济学与机器学习，它们的差异显而易见。如Breiman(2001)强调：传统统计方法与机器学习的根本分歧在于，
  • 前者在已知数据模型假设下聚焦参数估计和统计检验，
  • 而后者在不假设已知数据模型情况下最大化预测精度。
• 换言之，
  • 对计量经济学，参数估计先于预测精度；
  • 对机器学习，预测精度先于参数估计。
• 若考虑资产定价实证研究目标，
  • 计量经济学主要关注定价模型能否在样本内定价测试资产，
  • 而机器学习聚焦基于模型预测构建的组合能否在样本外实现最优风险调整收益。

12.5.2 机器学习与计量经济学的协同

在资产定价和因子投资领域，两种文化不应被视为对立力量，而应作为互补方法（Kelly和Xiu 2023）。计量经济学原理与机器学习预测能力的融合，可丰富我们的理解并提升投资策略效力。

例如，将计量经济学的因果检验纳入机器学习流程，有助于识别&验证背后有真实经济逻辑的预测因子，从而降低伪相关风险。
此外，计量经济学强调理解底层DGP可指导机器学习模型的特征选择，确保输入变量不仅是统计假象。这种综合方法也能促进机器学习模型的可解释性。例如，模型无关的可解释性工具可应用于机器学习模型，阐明输入特征与预测间关系，从而提供类似计量经济学模型的洞见（Ribeiro、Singh和Guestrin 2016）。
再者，计量经济学对不确定性和推断的严谨处理能增强机器学习在金融中的应用。例如，研究机器学习模型预测的渐近分布，能让投资者更细致地理解模型生成预测信号的风险和可靠性。

反过来，机器学习能揭示传统计量经济学方法可能忽略的新实证规律，从而丰富经济学和金融学的假设检验与理论发展。机器学习的数据驱动特性使其能发现金融数据中复杂的非线性模式和交互作用，这些可能并非立即显现或理论预期。例如，机器学习技术能识别大量市场指标和经济信号间错综复杂的关系，揭示资产收益或经济周期此前未被认识的预测因子。

总之，计量经济学严谨性与机器学习灵活性间的相互作用，为推进资产定价和因子投资提供了肥沃土壤。通过结合两种方法的优势——计量经济学对因果性、可解释性和严格推断的关注，与机器学习处理复杂非线性关系和大数据的能力——金融界能开发更稳健、深刻和有效的因子。这种互补协同凸显了金融研究中多学科视角的必要性，既要拥抱计量经济学的丰富传统，也要接纳机器学习的创新潜力（Varian 2014）。

12.6 结论

总结本章，我们反思了机器学习在资产定价和因子投资领域的变革性作用。机器学习算法与该领域的整合不仅增强了研究者和实践者的分析能力，更开启了金融建模与预测的新纪元。

本章同时强调了融合计量经济学理论与机器学习自适应能力的协同方法的重要性。这种多学科策略确保了我们开发的模型不仅预测能力强，而且立足经济原理并具可解释性。面对不断演进的市场动态，保持模型可信度与相关性需依赖这种平衡。

展望未来，机器学习在因子投资中的潜力看似无限。但这一征程并非没有挑战。过拟合、可解释性和稳健验证框架需求等问题仍是我们考量的重点。未来的征程无疑需要学界与业界的协同努力以有效应对这些挑战。随着我们持续探索这一激动人心的前沿领域，计量经济学智慧与机器学习创新的融合，有望在复杂的金融世界中释放更深刻的洞见并创造更有效的投资策略。