1 线性回归简介

1 线性回归应用场景

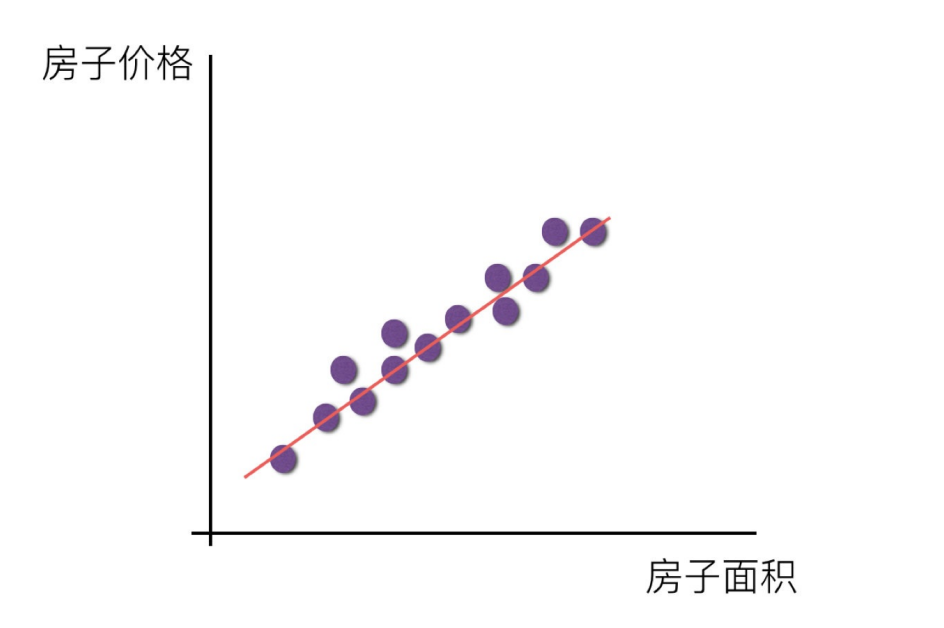
线性回归是一种用于分析自变量与连续型因变量之间线性关系的模型，其核心是通过拟合线性方程(y = w_1x_1 + w_2x_2 + ... + w_nx_n + b）来预测因变量或解释自变量的影响。由于其简单、可解释性强的特点，线性回归在多个领域有广泛应用。预测类场景（核心应用）包括房价预测、销售额 / 销量预测、能源消耗预测等。影响因素分析（解释性应用）上包括经济指标分析、医学健康分析等都可以使用线性回归算法进行预测。

2.线性回归的定义与公式

线性回归 (Linear regression) 是利用回归方程 (函数) 对一个或多个自变量 (特征值) 和因变量 (目标值) 之间关系进行建模的一种分析方式。这种函数是一个或多个称为回归系数的模型参数的线性组合。只有一个自变量的情况称为简单回归，大于一个自变量情况的叫做多元回归。（这反过来又应当由多个相关的因变量预测的多元线性回归区别，而不是一个单一的标量变量。）在线性回归中，数据使用线性预测函数来建模，并且未知的模型参数也是通过数据来估计。这些模型被叫做线性模型。最常用的线性回归建模是给定X值的y的条件均值是X的仿射函数。不太一般的情况，线性回归模型可以是一个中位数或一些其他的给定X的条件下y的条件分布的分位数作为X的线性函数表示。像所有形式的回归分析一样，线性回归也把焦点放在给定X值的y的条件概率分布，而不是X和y的联合概率分布（多元分析领域）。

特点：只有一个自变量的情况称为单变量回归，多于一个自变量情况的叫做多元回归

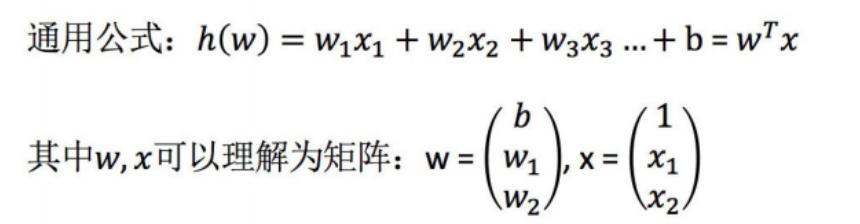
那么怎么理解呢？我们来看几个例子

期末成绩：0.7× 考试成绩 + 0.3× 平时成绩
房子价格 = 0.02× 中心区域的距离 + 0.04× 城市一氧化氮浓度 + (-0.12× 自住房平均房价) + 0.254× 城镇犯罪率

上面两个例子，我们看到特征值与目标值之间建立了一个关系，这个关系可以理解为线性模型。

3.线性回归的特征与⽬标的关系分析

线性回归当中主要有两种模型，⼀种是线性关系，另⼀种是⾮线性关系。在这⾥我们只能画⼀个平⾯更好去理解，所以都⽤单个特征或两个特征举例⼦。

线性关系

单变量线性关系：（一元线性回归）

y=mx+b

中学时，我们经常使用上面的方程来解一些数学问题，方程描述了变量 y 随着变量 x 而变化。方程从图形上来看，是一条直线。如果建立好这样的数学模型，已知 x 我们就可以得到预测的 $\hat{y}$ 值了。统计学家给变量带上了一个小帽子，表示这是预测值，以区别于真实观测到的数据。方程只有一个自变量 x，且不含平方立方等非一次项，因此被称为一元线性方程。

在对收入数据集进行建模时，我们可以对参数 m 和 b 取不同值来构建不同的直线，这样就形成了一个参数家族。参数家族中有一个最佳组合，可以在统计上以最优的方式描述数据集。那么监督学习的过程就可以被定义为：给定 N 个数据对 (x, y)，寻找最佳参数 m*和 b*，使模型可以更好地拟合这些数据。

上图给出了不同的参数，到底哪条直线是最佳的呢？如何衡量模型是否以最优的方式拟合数据呢？机器学习用损失函数（loss function）来衡量这个问题。损失函数又被称为代价函数（cost function），它计算了模型预测值 $\hat{y}$ 和真实值 y 之间的差异程度。从名字也可以看出，这个函数计算的是模型犯错的损失或代价，损失函数越大，模型越差，越不能拟合数据。统计学家通常使用$L(\hat{y}, y)$来表示损失函数。

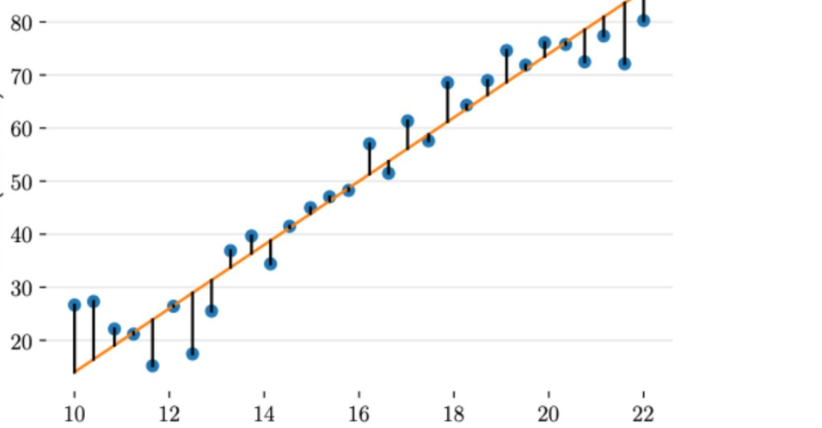
对于线性回归，一个简单实用的损失函数为预测值与真实值误差的平方。上图展示了收入数据集上预测值与真实值之间的误差。

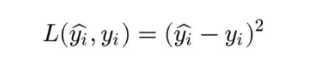
多变量线性关系 (多元线性回归)

现在我们把 x 扩展为多元的情况，即多种因素共同影响变量 y。现实问题也往往是这种情况，比如，要预测房价，需要考虑包括是否学区、房间数量、周边是否繁华、交通方便性等。共有 D 种维度的影响因素，机器学习领域将这 D 种影响因素称为特征（feature）。每个样本有一个需要预测的 y 和一组 D 维向量 $\mathbf{X}$ 。原来的参数 m 变成了 D 维的向量 $\mathbf{w}$ 。这样，某个 $y_i$ 可以表示成 $b + \sum_{d=1}^{D} w_d x_{i,d}$ ，其中 $x_{i,d}$ 表示第 i 个样本向量 $\mathbf{x}_i$ 中第 d 维特征值。

$y_i = b + \sum_{d=1}^{D} w_d x_{i,d} \qquad b = w_{D+1}\)\(y_i = \sum_{d=1}^{D+1} w_d x_{i,d}$

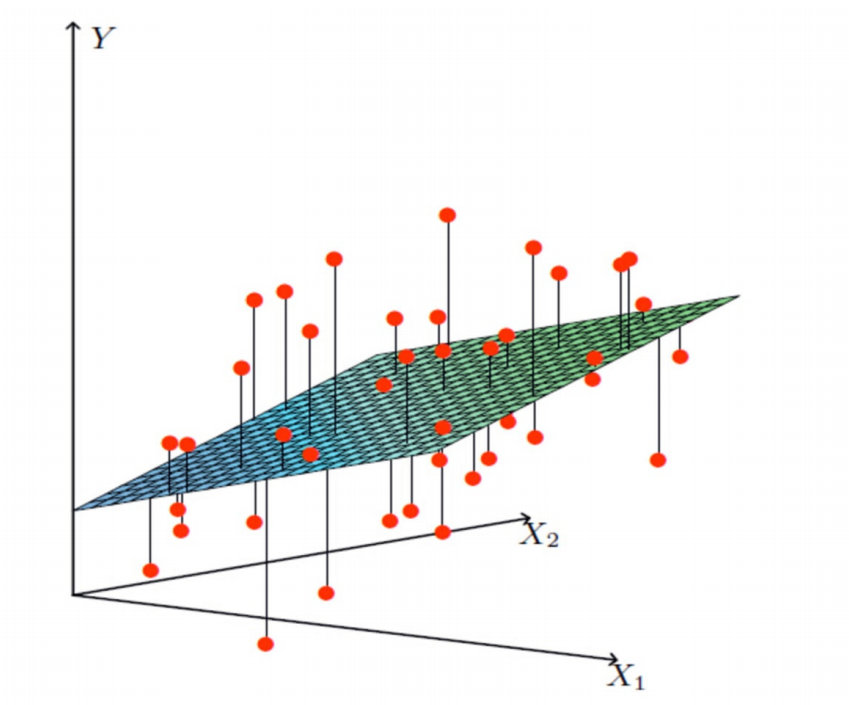
比一元线性回归更为复杂的是，多元线性回归组成的不是直线，是一个多维空间中的超平面，数据点散落在超平面的两侧。

⾮线性关系

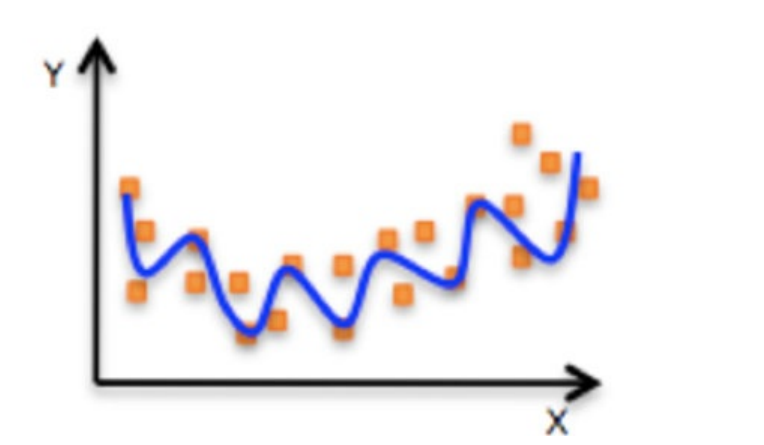
为什么会这样的关系呢？原因是什么？如果是⾮线性关系，那么回归⽅程可以理解为

4.最小二乘法

线性回归模型经常用最小二乘逼近来拟合，但他们也可能用别的方法来拟合，比如用最小化“拟合缺陷”在一些其他规范里（比如最小绝对误差回归），或者在桥回归中最小化最小二乘损失函数的惩罚.相反,最小二乘逼近可以用来拟合那些非线性的模型.因此，尽管“最小二乘法”和“线性模型”是紧密相连的，但他们是不能划等号的。

要使损失函数最小，可以将损失函数当作多元函数来处理，采用多元函数求偏导的方法来计算函数的极小值。

对于上面提到的：预测值与真实值之间的误差

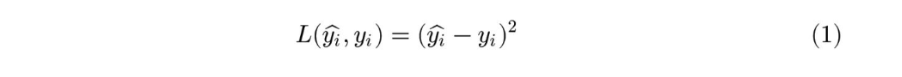
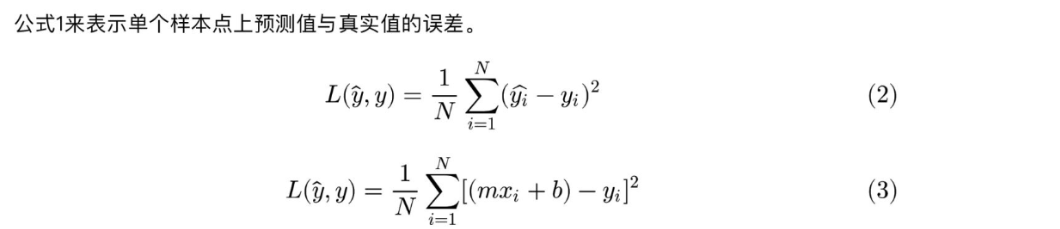
2.线性回归项目案例

1.简单线性回归分析广告投入与销售额关系

导入必要的库

import pandas as pd
import matplotlib.pyplot as plt  
from sklearn.linear_model import LinearRegression

加载数据

data = pd.read_csv("data(1).csv")

广告投入	销售额
29	77
28	62
34	93
31	84
25	59
29	64
32	80
31	75
24	58
33	91
25	51
31	73
26	65
30	84

数据预处理与可视化

plt.scatter(data['广告投入'], data['销售额'])
plt.xlabel('广告投入')
plt.ylabel('销售额')
plt.show()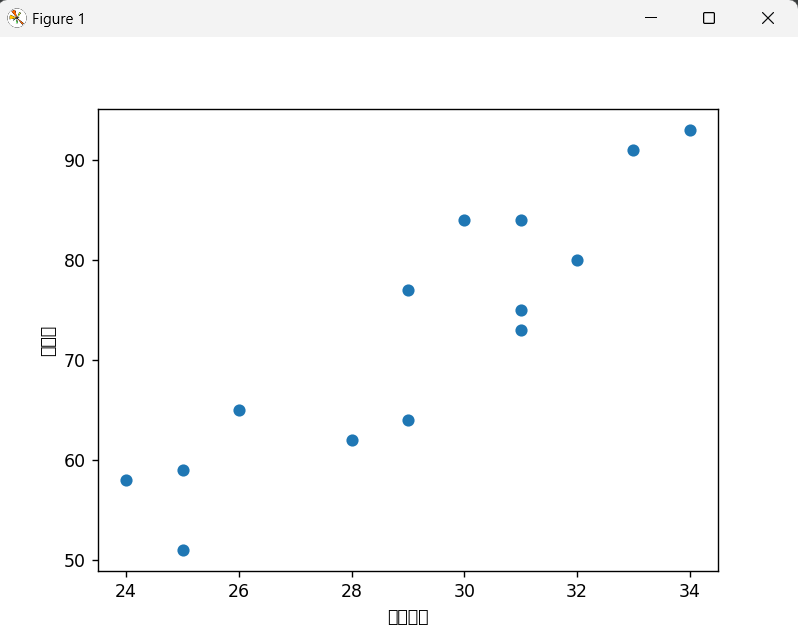

准备训练数据

x = data[["广告投入"]]  # 特征矩阵（自变量），需使用二维数组格式
y = data[['销售额']]   # 目标向量（因变量）

x：选取广告投入列作为特征
y：选取销售额列作为目标变量

创建并训练模型

estimator = LinearRegression(fit_intercept=True)  # 创建线性回归模型，包含截距项
estimator.fit(x, y)  # 训练模型

fit_intercept=True：指定模型包含截距项（即公式中的 b）
fit()方法通过最小二乘法计算最佳拟合参数

输出模型参数

print(estimator.coef_)        # 输出斜率（权重）
print(estimator.intercept_)   # 输出截距
print("线性回归模型为: y = {}x + {}".format(estimator.coef_[0][0], estimator.intercept_[0]))

coef_：模型的斜率（即广告投入对销售额的影响系数）
intercept_：模型的截距
模型公式：销售额 = 系数 × 广告投入 + 截距

评估模型

score = estimator.score(x, y)  # 计算R²得分
print(score)

score()方法返回模型的 R²（决定系数）
R² 表示模型对数据的拟合程度，取值范围 [0,1]，越接近 1 表示拟合效果越好

运行结果

[[3.73788546]]
[-36.36123348]
线性回归模型为: y = [[3.73788546]]x+[-36.36123348]
0.8225092881166945

完整代码

import pandas as pd
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegressiondata=pd.read_csv("data(1).csv")plt.scatter(data['广告投入'], data['销售额'])
plt.xlabel('广告投入')
plt.ylabel('销售额')
plt.show()x=data[["广告投入"]]
y=data[['销售额']]estimator=LinearRegression(fit_intercept=True)estimator.fit(x,y)
print(estimator.coef_)
print(estimator.intercept_)
print("线性回归模型为: y = {}x+{}".format(estimator.coef_,estimator.intercept_))
score=estimator.score(x,y)
print(score)

2.多元线性回归分析体重、年龄与收缩压关系

导入必要的库导入数据

import pandas as pd
from sklearn.linear_model import LinearRegression
data = pd.read_csv("多元线性回归.csv", encoding='gbk', engine='python')

计算相关系数矩阵

corr = data[["体重", "年龄", "血压收缩"]].corr()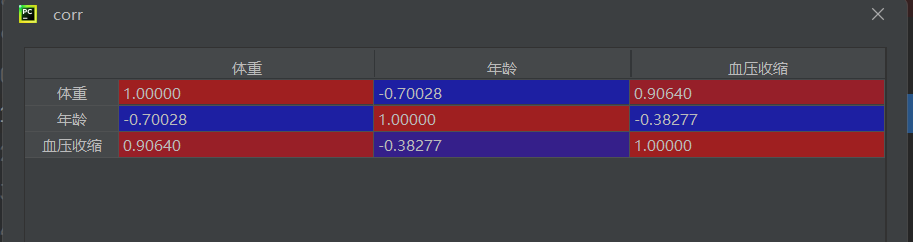

相关系数矩阵可帮助判断变量间的线性相关程度，绝对值越接近1表示越相关

准备训练数据

x = data[['体重', '年龄']]  # 特征矩阵（自变量）
y = data[['血压收缩']]     # 目标向量（因变量）

x：选取体重和年龄作为特征
y：选取血压收缩作为目标变量

创建并训练模型

lr_model = LinearRegression()
lr_model.fit(x, y)  # 训练模型

创建线性回归模型实例
fit()方法通过最小二乘法计算最佳拟合参数

模型评估

score = lr_model.score(x, y)  # 计算R²得分

score()方法返回模型的 R²（决定系数）
R² 表示模型对数据的拟合程度，取值范围 [0,1]

预测新数据

print(lr_model.predict([[80, 60]]))  # 预测体重80kg、年龄60岁的收缩压
print(lr_model.predict([[70, 30], [70, 20]]))  # 批量预测

predict()方法根据训练好的模型进行预测
输入需为二维数组，每行代表一个样本

输出模型参数

a = lr_model.coef_       # 获取系数
b = lr_model.intercept_  # 获取截距
print("线性回归模型为: y = {:.2f}x1 + {:.2f}x2 + {:.2f}.".format(a[0][0], a[0][1], b[0]))

运行结果

[[131.97426124]]
[[98.60219521][94.60003367]]
线性回归模型为: y = 2.14x1 + 0.40x2 + -62.96.

完整代码

import pandas as pd
from sklearn.linear_model import LinearRegression# 导入数据
data = pd.read_csv("多元线性回归.csv", encoding='gbk', engine='python')# 打印相关系数矩阵
corr = data[["体重", "年龄", "血压收缩"]].corr()# 第二步，估计模型参数，建立回归模型
lr_model = LinearRegression()
x = data[['体重', '年龄']]
y = data[['血压收缩']]lr_model.fit(x, y)  # 训练模型# 第四步，对回归模型进行检验
score = lr_model.score(x, y)  # sklearn statsmodes（数理统计这个专业）# 第五步，利用回归模型进行预测
print(lr_model.predict([[80, 60]]))
print(lr_model.predict([[70, 30], [70, 20]]))"""
a:自变量系数
b:截距
"""
a = lr_model.coef_
b = lr_model.intercept_
print("线性回归模型为: y = {:.2f}x1 + {:.2f}x2 + {:.2f}.".format(a[0][0], a[0][1], b[0]))
# 线性回归模型为: y = 2.14x1 + 0.40x2 + -62.96.