A题解的token计算

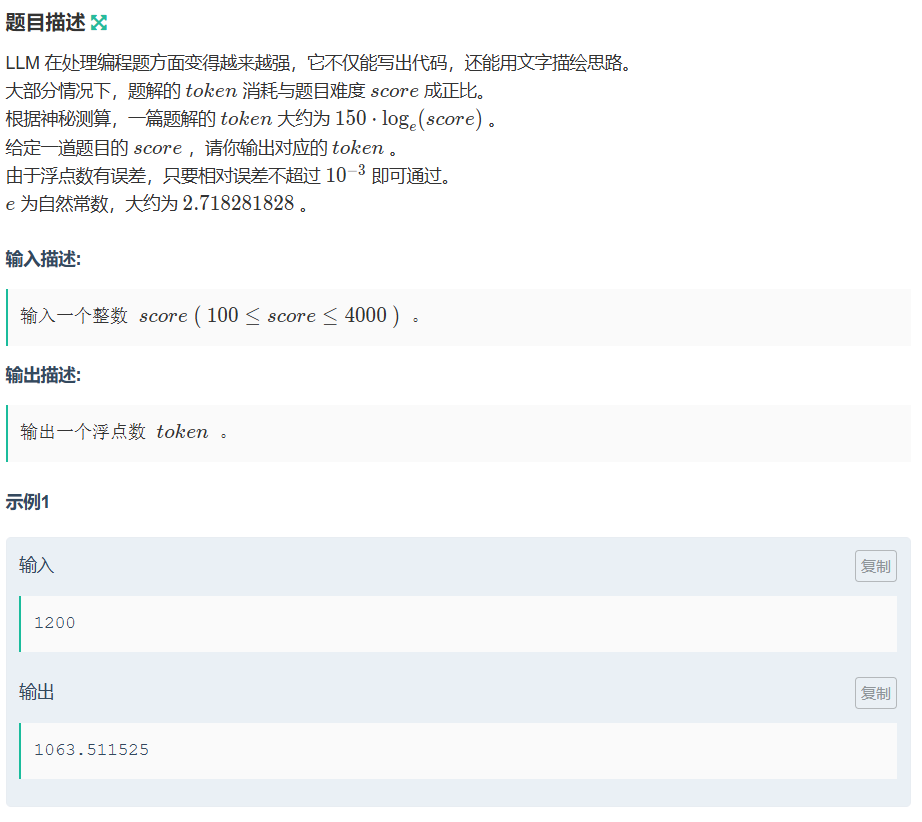
要记住c++中的对数函数：

log(n) 是自然对数（以e为底）ln(n
log10(n) 是以10为底的对
log1p(n) 是ln(1+n)，提供更高的数值精
log2(n) 是以2为底的对
logl(n) 和 log10l(n) 是long double版

#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<iostream>
#include<bits/stdc++.h>
#define ll long long 
using namespace std;
int main(){ios::sync_with_stdio(false);        // 禁用同步cin.tie(nullptr);                   // 解除cin与cout绑定double e = 2.718281828;double n;cin >> n;double w = 150 / log2l(e)* log2l(n) ;cout << setprecision(6) << w << endl;return 0;
}

B 76修地铁

这题你得先理解图：黄色是普通火把；红色是红石火把；粉色是普通铁轨；灰色是动力铁

#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<iostream>
#include<bits/stdc++.h>
#define ll long long 
using namespace std;
int main(){ios::sync_with_stdio(false);        // 禁用同步cin.tie(nullptr);                   // 解除cin与cout绑定int n;cin >> n;int w = (n / 5) * 2;//普通火把int q = ((n + 5) / 10) * 1;//红石火把int r = (n / 20) * 3;//普通铁轨int t = n * 2 - r / 3 * 2;//动力铁轨cout << w << " " << q << " " << r << " " << t << endl;return 0;
}

C76选数

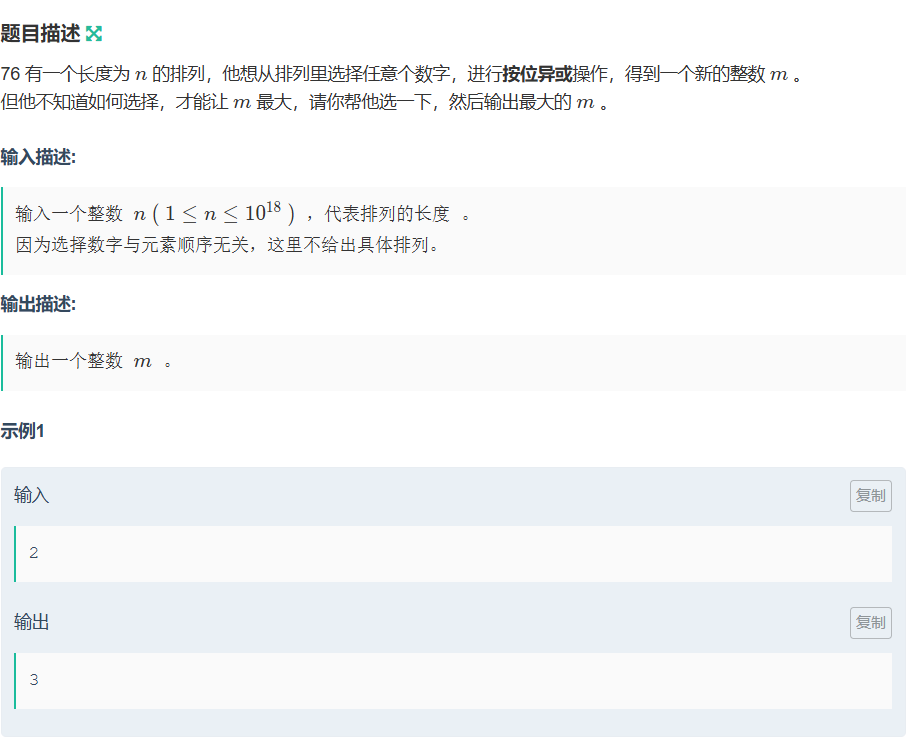
最大值就是在n所有二进制为都满的情况下（选数的话也是选二进制对应的十进制值）

#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<iostream>
#include<bits/stdc++.h>
#define ll long long 
using namespace std;
int main(){ios::sync_with_stdio(false);        // 禁用同步cin.tie(nullptr);                   // 解除cin与cout绑定ll n;cin >> n;ll w = 1;ll sum = 0;while (n > 0) {sum += w;n /= 2;w *= 2;}cout << sum << endl;return 0;
}

D76构造

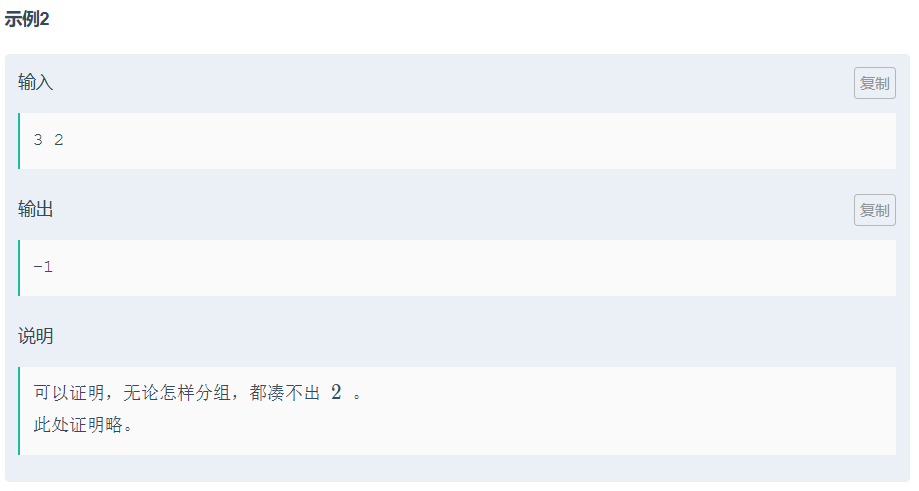
把他当作二进制看：

1的gcd()=1所以m为奇数 不成立

n组成的数最大设为max_n，max_n=n的二进制位都为1；max_n<m 不成立

成立的打印：

m二进制为1的位置转化成十进制当作一个区间（先省略掉1），剩下的和1组成一个大区间

#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<iostream>
#include<bits/stdc++.h>
#define ll long long 
using namespace std;
int n, m;
int main() {ios::sync_with_stdio(false);        // 禁用同步cin.tie(nullptr);                   // 解除cin与cout绑定cin >> n >> m;int sum = 0;int y = m;int x = 1;vector<ll> a;while (y > 0) {if (y % 2 == 1 && x != 1) {a.push_back(x);sum++;}y /= 2;x *= 2;}int y0 = n;int x0 = 1;while (y0 > 0) {y0 /= 2;x0 *= 2;}if (m % 2 == 0 || x0 <= m) {cout << -1 << endl;}else {for (int i = 0; i < a.size(); i++) {cout << a[i] << " ";}for (int i = 1; i <= n; i++) {int j = 0;for (j = 0; j < sum; j++) {if (i == a[j]) {break;}}if (j == sum) {cout << i << " ";}}cout << endl;cout << sum + 1 << endl;for (int i = 1; i <= sum; i++) {cout << i << " " << i << endl;}cout << sum + 1 << " " << n << endl;}return 0;
}

Eqcjj寄快递

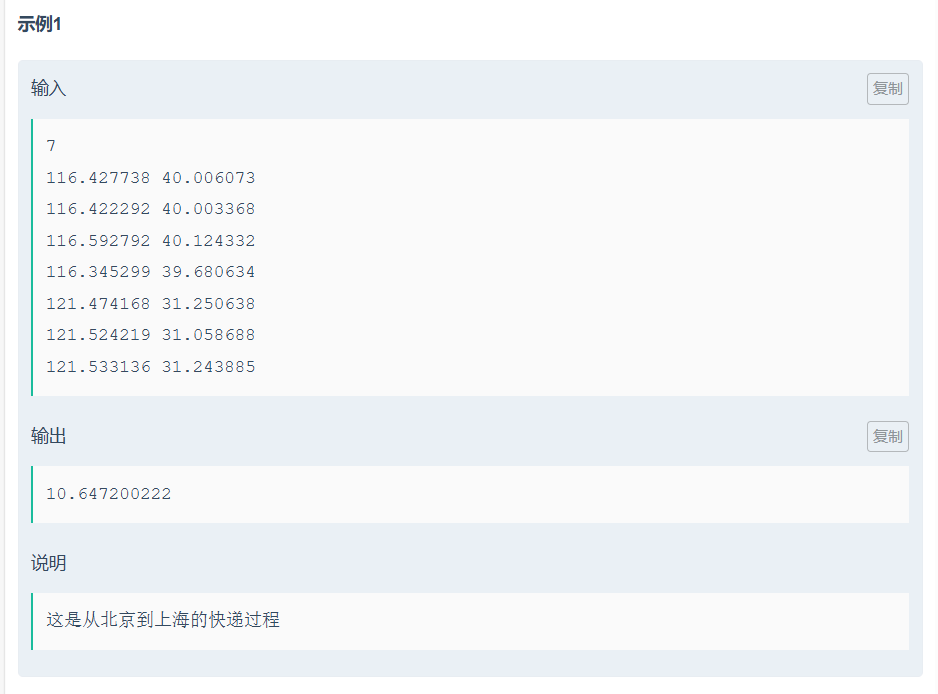
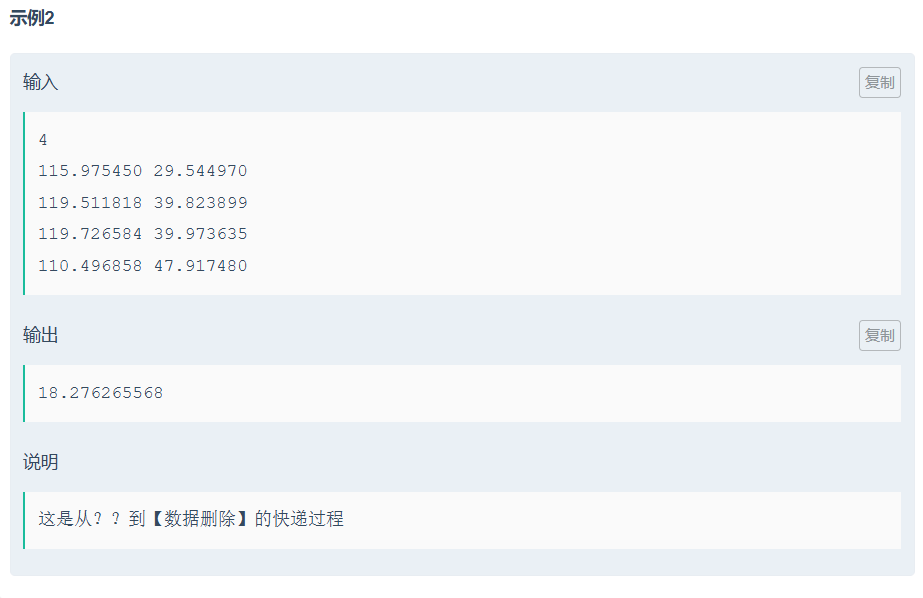
纯纯数学题，就是求 $ti=2*ki+2*\frac{ei}{ki}$ ,然后求导，但要注意ki的最小值不能为负数

得出ki=log2l(b[i] * ln2)时，ti最小，但ki<0时不成立，ki取0

E幂中幂plus

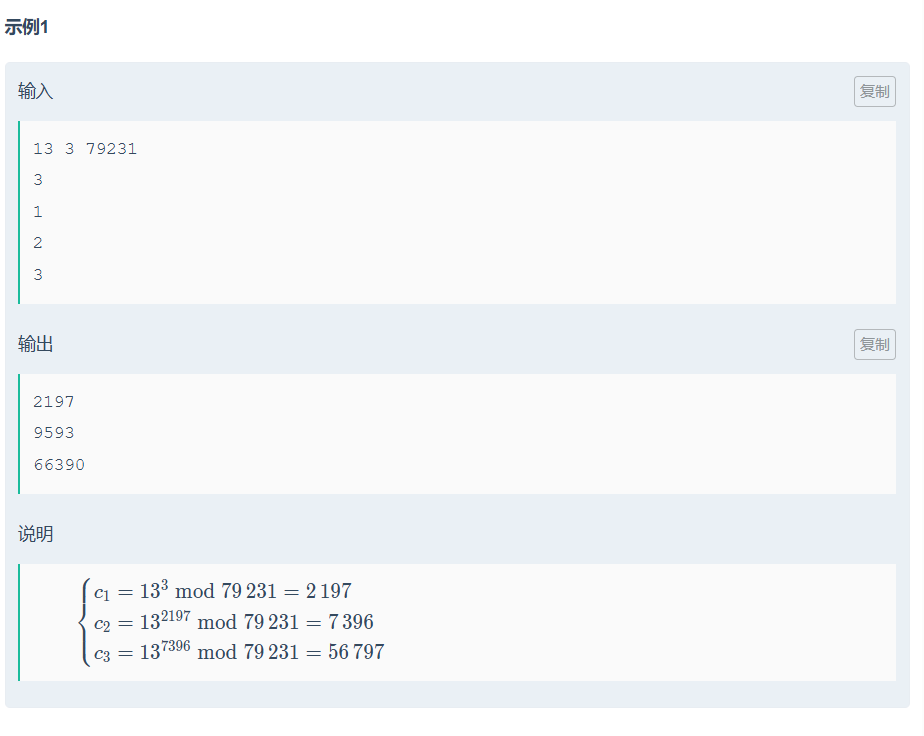
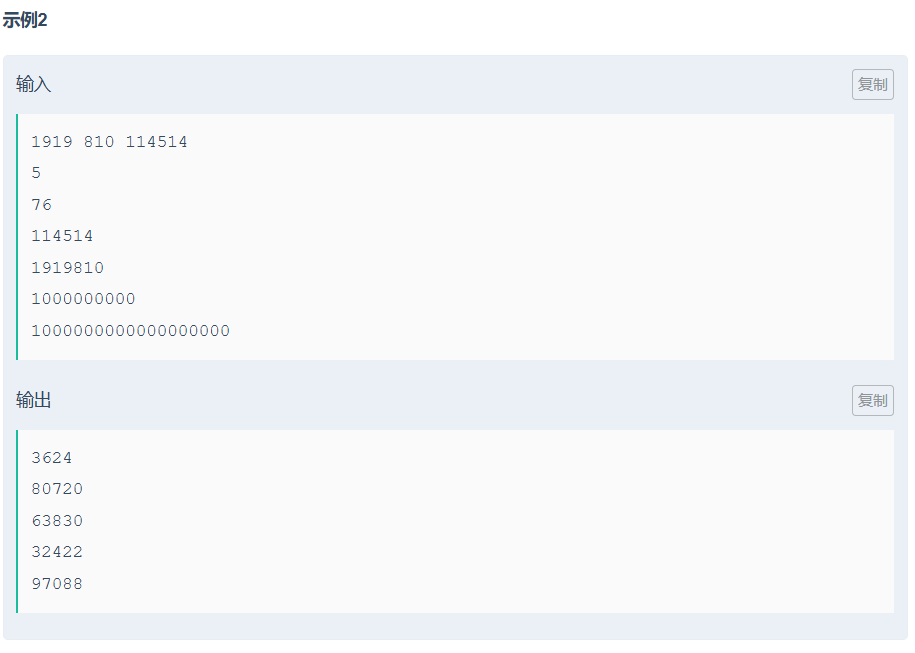找规律+快速幂+前缀和
m只有1e6 且每次的结果只与当前的c有关故一定会有循环
但是不一定从第一个数开始循环

base可能很大可以一开始先对base取一次模

前缀和下标从1开始

#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<iostream>
#include<bits/stdc++.h>
#define ll long long 
using namespace std;
ll base, c, mod;
int q;
ll k;
ll power(ll x, ll y) {ll sum = 1;x %= mod;while (y > 0) {if (y % 2 == 1) {sum = sum * x % mod;}x = x * x % mod;y /= 2;}return sum;
}
int main() {ios::sync_with_stdio(false);        // 禁用同步cin.tie(nullptr);                   // 解除cin与cout绑定cin >> base >> c >> mod;base %= mod;if (mod==1||base==0) {cin >> q;for (int i = 0; i < q; i++) {cin >> k;cout << 0 << endl;}}else if (base == 1) {cin >> q;for (int i = 0; i < q; i++) {cin >> k;cout << k%mod << endl;}}else{vector<ll> a;map<ll, bool>p;ll w;while (true) {w = power(base, c);if (p.find(w) == p.end()) {p.insert({ w,true });a.push_back(w);}else {break;}c = w;}int j;for (j = 0; j < a.size(); j++) {if (a[j] == w) {break;}}vector<ll> b(a.size() + 1);b[0] = 0;for (int i = 1; i <= a.size(); i++) {b[i] = (b[i-1] + a[i - 1]) % mod;}int z = a.size() - j;cin >> q;for (int i = 0; i < q; i++) {cin >> k;if (k > a.size()) {cout << ((b[a.size()] - b[j] + mod) % mod * (((k - j) / z) % mod) % mod + b[j  + (k - j) % z]) % mod << endl;}else {cout << b[k ]%mod << endl;}}}return 0;
}

前缀和下标从0开始：

/*
这种容易犯错
*/
#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<iostream>
#include<bits/stdc++.h>
#define ll long long 
using namespace std;
ll base, c, mod;
int q;
ll k;
ll power(ll x, ll y) {ll sum = 1;while (y > 0) {if (y % 2 == 1) {sum = sum * x % mod;}x = x * x % mod;y /= 2;}return sum;
}
int main() {ios::sync_with_stdio(false);        // 禁用同步cin.tie(nullptr);                   // 解除cin与cout绑定cin >> base >> c >> mod;base %= mod;if (mod==1||base==0) {cin >> q;for (int i = 0; i < q; i++) {cin >> k;cout << 0 << endl;}}else if (base == 1) {cin >> q;for (int i = 0; i < q; i++) {cin >> k;cout << k%mod << endl;}}else{vector<ll> a;map<ll, bool>p;ll w;while (true) {w = power(base, c);if (p.find(w) == p.end()) {p.insert({ w,true });a.push_back(w);}else {break;}c = w;}int j;for (j = 0; j < a.size(); j++) {if (a[j] == w) {break;}}for (int i = 1; i < a.size(); i++) {a[i] = (a[i] + a[i - 1]) % mod;}int z = a.size() - j;cin >> q;for (int i = 0; i < q; i++) {cin >> k;if (k > a.size()) {cout << ((a[a.size() - 1] - (j - 1 >= 0 ? a[j - 1] : 0)+ mod) % mod * (((k - j) / z) % mod) % mod + (j - 1 + (k - j) % z >= 0 ? a[j - 1 + (k - j) % z] : 0)) % mod << endl;}else {cout << a[k - 1]%mod << endl;}}}return 0;
}