第 4 章线性算子(Linear Operators)

That confusions of thought and errors of reasoning

still darken the beginnings of Algebra,

is the earnest and just complaint of sober and thoughtful men.

(思维混乱和推理错误

仍然使代数的开端变得模糊不清，

这是清醒而富于思考的人诚挚而公正的抱怨。)

---------------------------------------------------William Rowan Hamilton先生

4.1 维数公式(The dimension formula)

4.2 线性变换矩阵(The matrix of a linear transformation)

4.3 线性算子(或算符)(Linear operators)

4.4 特征向量(Eigenvectors)

4.5 特征多项式(The characteristic polynomial)

4.6 三角形和对角形(Triangular and diagonal forms)

4.7 Jordan形式(Jordan form)

4.1 维数公式(The dimension formula)

从一个域(field)(译注：见3.2) F 上的向量空间到其上的另一个向量空间的一个线性变换(A linear transformation) T:V ⟶ W 是一个与加法和标量乘兼容的映射：

(4.1.1) $T(v_{1} + v_{2}) = T(v_{1}) + T(v_{2})$ 和 $T(cv_{1}) = c T(v_{1})$ ( 对于 V 中的所有 $v_{1}$ 和 $v_{2}$ 以及 F中的所有 c )。这可类比于群的同态(homomorphism)，并且称其为同态也合适。线性变换与任意线性组合兼容：

(4.1.2) $T(\sum_{i}v_{i} c_{i}) = \sum_{i}T(v_{i}) c_{i}$ 。

左乘一个其项来自域 F 的 m×n 矩阵 A 而发送 X ⇝ AX (译注：“⇝”为右向波浪箭头(squiggle))的映射

(4.1.3) $F^{n}\overset{A}{\longrightarrow}F^{m}$

是一个线性变换。事实上，对于矩阵 A，有 $A(X_{1} + X_{2}) = AX_{1} + AX_{2}$ ，且 $A(cX ) = cA(X )$ 。

若 $B = (v_{1} ,...,v_{n})$ 是域 F 上的向量空间 V 的一个子集，则发送 X ⇝ BX 的映射 $F^{n} \longrightarrow V$ 的映射是一个线性变换。另一个线性变换的例子：令 $P_{n}$ 为实数多项式函数

(4.1.4) $a_{n} t^{n} + a_{n-1} t^{n-1} + ... + a_{1}t + a_{0}$

为最多n阶的向量空间，则其导数 $\frac{d}{dt}$ 定义了一个从 $P_{n}$ 到 $P_{n-1}$ 的线性变换。存在两个与线性变换紧密联系的重要子空间：线性变换的核 (kernel)及其像(image)。

(4.1.5) ker T = T 的核 = { v∈V |T(v) = 0 } ，

img T = T 的像 = { w∈W | w = T(v ) (对某个 v∈V ) } 。

核通常称为线性变换的零空间(nullspace)。由于我们可以基于与同态(homomorphisms)的类比进行猜测，核是的V 一个子空间，而像是 W 的一个子空间。

这一节的主要结论融合于下面的一个定理中。

定理 4.1.6 (维数公式): 令 T:V ⟶ W 为一个线性变换，则

dim(ker T ) + dim(im T ) = dim(V ) 。

一个线性变换 T 的零化度 (nullity)和 秩(数) (rank，或阶数)分别是核和像的维数，一个矩阵A 的零化度和秩按类似方式定义。使用这个术语，定理(4.1.6)就成为

(4.1.7) 零化度 + 秩 = V的维数。

定理 4.1.6 的证明：

我们假设 V 是有限维的，比如是 n 维的。令 k 为 ker T 的维数，并令 $(u_{1}, ..., u_{k})$ 为核的一组基，我们将这个集合扩展成 V 的一组基：

(4.1.8) $(u_{1}, ..., u_{k}; v_{1}, ..., v_{n-k})$ 。

(参见(3.4.15))。对于 i = 1,...,n - k, 令 $w_{i} = T(v_{i})$ 。若我们能证明 $C=(w_{1},..., w_{n-k})$

是像的一组基，则将能推导出像的维数是 n – k ,这将能证明这个定理。

我们必需证明 C 生成(或“张成”)(spans)这个像并且是一个线性无关的集合。令 w 为像的一个元素，则对于 V 中的某个 v 有 w = T(v)。我们根据这组基写出这个v :

$v = a_{1} u_{1} + ... + a_{k} u_{k} + b_{1} v_{1} + ... + a_{n-k} u_{n-k}$ ,

并应用线性变换 T ，注意 $T(u_{i})=0$ :

$w = T(v) = b_{1} w_{1} + ... + b_{n-k} w_{n-k}$ 。

因此，C生成 w 。

接下来，我们证明C是线性无关的。假设我们有一个线性关系

(4.1.9) $c_{1} w_{1} + ... + c_{n-k} w_{n-k} = 0$ 。

令 $v = c_{1} v_{1} + ... + c_{n-k} v_{n-k}$ ，其中， $v_{i}$ 是 (4.1.8) 中的向量。则

$T(v) = c_{1} w_{1} + ... + c_{n-k} w_{n-k} = 0$ ,

因此，v 在零空间中，我们根据零空间的基 $(u_{1}, ..., u_{k})$ 来记 v ，比如记为 $v = a_{1} u_{1} + ... + a_{k} u_{k}$ 。则

$-a_{1}u_{1} - ... - a_{k} u_{k} + c_{1} v_{1} + ... + c_{n-k} v_{n-k} = - v + v = 0$ 。

但是基 (4.1.8) 是线性无关的，因此， $-a_{1} = 0,...,-a_{k} = 0$ ，并且 $c_{1 }= 0 ,...,c_{n-k} = 0$

。关系 (4.1.9) 是平凡的(译注：即只有系数全部为零才满足这个表达式，这种情况对我们是没有意义的)，因此，C 是独立的。

当T 是一个使用矩阵A (4.1.3)进行的左乘的时候，T 的核(A 的零空间)是齐性方程组 AX = 0 的解集。T 的像是列空间(column space)(由A 的列生成的空间)，其也是 $F^{m}$ 中使得线性方程 AX = B 有解(3.4.6) 的向量 B 的集合。

一个熟悉的事实是，齐性方程 AX = 0 的解加上非齐性方程 AX = B 的特解 $X_{0}$ ，我们就得到了非齐性方程的所有解。换言之，AX = B 的解集是 $F_{n}$ 中零空间 N 的可加陪集(coset) $X_{0}+N$ 。

一个其行列式不为零 0 的 n×n 矩阵是可逆的。对于每一个B ，方程组 AX = B 具有唯一解。在这种情况下，零空间是 {0} ，列空间是整个空间 $F^{n}$ 。在另一方面，若行列式是 0 ，零空间 N 具有正的维数，而其像 (列向量) 具有小于n 的维数。并非所有方程 AX = B 都有解，而有解的方程可以具有超过一个解，因为解集是 N 的陪集。

4.2 线性变换矩阵(The matrix of a linear transformation)

从一个列向量空间到另一个列向量空间的每一个线性变换都是一个左乘矩阵的运算。

引理 4.2.1 令 $T : F^{n} \longrightarrow F^{m}$ 为一个列向量空间之间的线性变换，并令 $T(e_{j})$ 的坐标向量为 $A_{j} = (a_{1j},...,a_{mj})^{t}$ 。令 A 为列为 $A_{1} ,...,A_{n}$ 的 n×n 矩阵。则 T 在 $F^{n}$ 的向量上等效于左乘 A 。

证明：

$T( X ) = T(\sum_{j}e_{j} x_{j}) = \sum_{j}T(e_{j})x_{j} = \sum_{j}A_{j} x_{j} = AX$ 。

例如，令 $c=\cos{\theta}$ , $s=\sin{\theta}$ 。则平面围绕原点逆时针进行角度为θ 的旋转 $\rho:\mathbb{R}^{2} \rightarrow :\mathbb{R}^{2}$ 是一个线性变换。其变换矩阵为

(4.2.2) $R=\begin{bmatrix} c&-s\\ s&c \end{bmatrix}$ 。

我们来验证用这个矩阵旋转平面的乘法。我们将向量 X 记为 $r(\cos{\alpha},\sin{\alpha})^{t}$ ，其中，r 是 X 的长度，令 $c^{'} = \cos{\alpha}$ 和 $s^{'} = \sin{\alpha}$ 。正弦和余弦的加法公式表明

$RX=r\begin{bmatrix} c&-s\\ s&c \end{bmatrix}\begin{bmatrix} c^{'}\\ s^{'} \end{bmatrix}=r\begin{bmatrix} cc^{'}-ss^{'} \\ sc^{'}+cs^{'} \end{bmatrix}= r\begin{bmatrix} \cos{(\theta+\alpha)} \\\sin{(\theta+\alpha)}\end{bmatrix}$ 。

因此，RX可由X旋转至 θ 而获得，正如断言所示。

对于两个空间V 和 W，一旦选定了其基，我们就可以使用任何线性变换 T:V ⟶ W 进行与引理 4.2.1 类似的计算。若 $\mathbf{B}= (v_{1}, ..., v_{n})$ 是V 的一组基，我们用简记形式 T (B)来表示超向量(hypervector)(译注：高维向量)

(4.2.3) $T(\mathbf{B}) = (T(v_{1}),..., T(v_{n}))$ 。

若 $v = BX = v_{1} x_{1} + ... + v_{n} x_{n}$ ，则

(4.2.4) $T(v) = T(v_{1}) x_{1} + ...+ T(v_{n}) x_{n} = T(\mathbf{B})X$ 。

命题 4.2.5 令 T : V ⟶ W 为一个线性变换，并令 $\mathbf{B} = ( v_{1} ,..., v_{n} )$ 和 $\mathbf{C} = ( w_{1} ,..., w_{n} )$ 分别为 V 和 W 的基。令 X 为一个任意向量 v 关于基B 的坐标向量，并令 Y 为其像 T (v) 的坐标向量。因此，v = BX 且 T = CY 。则存在一个具有对偶属性的 m ×n 矩阵 A ，使得

(4.2.6) T (B) = CA 且 AX = Y 。

这个矩阵 A 称为 T 关于两个基的变换矩阵。(4.2.6) 中任一属性都刻画了这个矩阵。

证明：

我们将 $T(v_{j})$ 写成基 C 的一个线性组合，比如写成

(4.2.7) $T(v_j) = w_{1} a_{1j} + ...+ w_{m} a_{mj}$ ，

我们将系数汇编入一个列向量 $A_{j} = (a_{1j},..,a_{mj})^{t}$ ，因此， $T(v_{j}) = \mathsf{C}A_{j}$ 。若 A 是其列为 $A_{1} ,...,A_{n}$ 的矩阵，则

(4.2.8) $T(\mathbf{B}) = ( T(v_{1}),..., T(v_{n}) ) = (w_{1} ,... ,w_{n} )\begin{bmatrix} &\cdots& \\ \vdots&A&\vdots \\ &\cdots& \end{bmatrix}=\mathbf{CA}$ 。

正如断言。接下来，若 v = BX ，则

T(v) = T(B)X = CAX 。

因此，T(v) 的坐标向量(其命名为 Y ) 等于 AX 。

由这两个基 (3.5.3) 所确定的同构 $F^{n} \rightarrow V$ 和 $F^{m} \rightarrow W$ 有助于解释 T 和 A 之间的关系。若我们用这些同构将 V 和 W 与 $F^{n}$ 和 $F^{m}$ 关联起来，则 T 对应于乘以 A ，如下图所示：

(4.2.9)

沿着两条路径从 $F^{n}$ 到 W 给出相同的答案。具有这种属性的图(diagrams)称为交换图(commutative)。本书中所有的图都是可交换的。

因此，一旦选定了有限维向量空间 V 和 W 的基，它们之间的任何线性变换都对应着矩阵乘法。这是一个很好的结果，但如果我们改变基，结果会更好。

定理 4.2.10

(a) 向量空间的形式：令 T : V ⟶ W 为一个有限维向量空间之间的线性变换。则分别存在 V 和 W 的基 B 和 C ，使得 T 的矩阵关于这些基具有形式

(4.2.11)

其中 $I_{r}$ 是 r × r 恒等矩阵，且 r 是 T 的秩。

(b) 矩阵形式：已知一个 m × n 矩阵 A ，则存在可逆矩阵 P 和Q 使得 $A^{'} = Q^{-1} AP$ 具有上述 (a) 中的形式。

证明：

令 $(u_{1} ,..., u_{k})$ 为 T 之核的一个基，我们将此集合扩展至 V 的一个基 B ，首先列出附加的向量，比如 $(v_{1} ,..., v_{r} ;u_{1} ,..., u_{k})$ ，其中 r + k = n 。令 $w_{i }= T(v_{i})$ 。则如 (4.1.6) 的证明所示，我们可以看到， $( w_{1} ,... , w_{r})$ 是T 的像的一个基。我们将这个集合扩展至 W 的一个基 C ，比如 $( w_{1} ,..., w_{r} ;z_{1} ,..., z_{k})$ ，最后列出附加的向量。则 T 关于这些基的矩阵形如 (4.2.11)。

定理的 (b) 部分可以通过行和列运算来证明。证明见练习 2.4。

这个定理是一系列后续结果的原型。它展示了在向量空间中处理没有固定基(或坐标)的优势，因为任意线性变换的结构都可以用一个非常简单的矩阵 (4.2.11) 来描述。但为什么 (a) 和 (b) 被认为是同一定理的两个版本呢？为了回答这个问题，我们需要分析当我们选择其他基时，线性变换矩阵的变化方式。

令 A为T 关于V 和 W 的基B 和 C 的矩阵，如 (4.2.6)中所示，且令 $\mathbf{B}^{'} = (v_1^{' },..., v_n^{'} )$ 和 $\mathsf{C}^{'} = (w_1^{'} ,..., w_m^{'} )$ 分别为V 和 W 的新的基，我们可以通过一个逆 n × n 矩阵 P 将新的基 $\mathsf{B}^{'}$ 与旧的基 B 关联起来，如 (3.5.11)中所示。类似地，通过一个可逆 m × m 矩阵 Q 将新的基 $\mathsf{C}^{'}$ 与旧的基 C 关联起来。这些矩阵具有属性

(4.2.12) $\mathbf{B}^{'} = \mathbf{B}P$ ， $PX^{'} = X$ 和 $C^{'} = CQ$ ， $QY^{' }= Y$ 。

命题 4.2.13 令 A 为关于已知基 B 和 C 的线性变换 T 的矩阵。则：

(a) 假设新的基 $\mathsf{B}^{'}$ 和 $\mathsf{C}^{'}$ 通过矩阵 P 和 Q 关联起来，如上所示。则 T 关于新的基的矩阵是

$A^{'} = Q^{-1}A P$ 。

(b) 表示T 关于其它基的矩阵 $A^{'}$ 是那些形如 $A^{'} = Q^{-1}A P$ 的矩阵，其中 Q 和 P 可以是任意合适大小的逆矩阵。

证明：

(a) 将 $X = PX^{' }$ 和 $Y = QY^{' }$ 代入公式 Y = AX (4.26) ,得到 $QY^{'} = APX^{' }$ , 因此 $Y^{' }= (Q^{-1}AP )X^{'}$ 。由于 $A^{'}$ 是使得 $A^{'} X^{'} = Y^{' }$ 的矩阵，这明表 $A^{'} = Q^{-1}A P$ 。

(b) 部分成立，因为基变换矩阵可以是任何可逆矩阵 (3.5.9)。

从命题可知，该定理的两部分是等价的。为了从(b)推导出(a)，我们假设已知线性变换T ，并且我们首先任意选择V 和W 的基，得到矩阵 A 。(b)部分告诉我们，存在可逆矩阵 P 和 Q，使得 $A^{'} = Q^{-1}A P$ 具有形式(4.2.11)。当我们使用这些矩阵来改变V和W的基时，矩阵 A 变为 $A^{'}$ 。

为了从 (a) 推导出 (b)，我们将任意矩阵A 视为列向量上“左乘A”的线性变换的矩阵。则 A 是T 关于 $F_{n}$ 和 $F_{m}$ 的标准基的矩阵，且(a) 保证P 和Q 的存在，使得 $A^{'} = Q^{-1}A P$ 具有形式(4.2.11)。

这里我们还学到了一些关于矩阵乘法的奇妙之处，因为矩阵左乘是一个线性变换。任意矩阵 A 的左乘与形式为 (4.2.11) 的矩阵的左乘相同，只是参考的坐标不同。

以后，我们经常会用两种等价的方式表述一个结果：向量空间形式和矩阵形式，而无需证明这两种形式是等价的。然后，我们会给出任何看起来更容易写出来的证明。

我们可以利用定理 4.2.10 推导出矩阵乘法的另一个有趣性质。设 N 和 U 分别表示变换 $A: F_{n} \rightarrow F_{m}$ 的零空间和列空间。因此，N 是 $F_{n}$ 的子空间，U 是 $F_{m}$ 的子空间。设 k 和 r 分别表示 N 和 U 的维数。因此，k (nullity)是 A 的零化度，r 是它的秩。

左乘转置矩阵 $A^{t}$ 按相反的方向定义了一个变换 $A^{t}:F_{m} \rightarrow F_{n}$ ，因此 $A^{t}$ 有两个(含)以上子空间，零空间 $N_{1}$ 和列空间 $U_{1}$ 。在这里 $U_{1}$ 是 $F_{n}$ 的子空间， $N_{1}$ 是 $F_{m}$ 的子空间，令 $k_{1}$ 和 $r_{1}$ 分别表示 $N_{1}$ 和 $U_{1}$ 的维数。根据定理 4.1.6 ，我们有 k + r = n 以及 $k_{1} + r_{1} = m + n$ 。下述定理 4.2.14 给出了这些整数之间的更多关系。

定理 4.2.14 一个矩阵的秩等于其转置的秩，即，根据上述记法，有 $r_{1}=r$ 。

证明：

令 P 和 Q 为使得 $A^{'} = Q^{-1}A P$ 具有形式 (4.2.11) 的逆矩阵。首先，我们注意到这个断言对于矩阵 $A^{'}$ 是显然的。接下来，我们验证下图中的关系

(4.2.15)

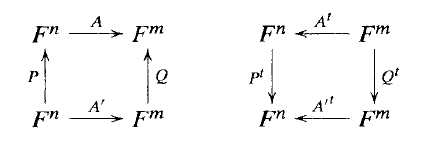
垂直箭头是双射映射。因此，在左图中，Q 将 $A^{'}$ 的列空间 (与 $A^{'}$ 相乘的像)双射到 A 的列空间。这两个列空间的维度(即 A 和 $A^{'}$ 的秩)相等。同样， $A^{t}$ 和 ${A^{'}}^{t}$ 的秩也相等。因此，为了证明该定理，我们可以用 $A^{'}$ 代替矩阵 A 。这将证明简化为矩阵 (4.2.11) 的平凡情况。

我们可以重新解释转置矩阵 $A^{t}$ 的秩 $r_{1}$ 。根据定义，它是 $A^{t}$ 的列向量所张成的空间的维数，也可以理解为 A 的行所张成的行向量空间的维数。因此，人们通常指称 $r_{1}$ 为 A 的行秩，指称 r 为 A 的列秩。

行秩是矩阵中独立行的最大个数，列秩是矩阵中独立列的最大个数。定理4.2.14可以表述如下：

推论 4.2.16 一个m × n 矩阵 A 的行秩和列秩是相等的。

4.3 线性算子(或算符)(Linear operators)

在本节中，我们研究线性变换 T : V ⟶ V，它将一个向量空间到其自射的映射。它们称为线性算子(或算符)(linear operator)。(用于)左乘的一个具有(定义)域 P 中元素的 n × n 矩阵(方阵)就定义了一个列向量空间 $F^{n}$ 上的线性算子。

例如，令 c = cos(θ) , s = sin(θ) 。则旋转矩阵 (4.2.2)

$\begin{bmatrix} c&-s\\ s&c \end{bmatrix}$

就是一个平面 $\mathbb{R}^{2}$ 上的线性算子。

维数公式 dim(ker T ) + dim(im T ) = dim(V ) 对于线性算子仍然有效。但这里，由于定义域(domain)和值域(range)相同，我们获得了可以与公式结合的额外信息。T 的核和像都是 V 的子空间。

命题 4.3.1 令 K和 W 分别表示一个线性算子T在一个有限维向量空间V上的核和像。则

(a) 下述条件是等价的：

• T 是双射的，

• K = {0}，

• W = V 。

(b) 下述条件是等价的：

• V 是直和 K ⨁ W ，

• K ∩ W = {0} ，

• K + W = V 。

证明：

(a) T 是双射的，当且仅当核 K 为零，则像 W 是整个空间 V。如果核为零，则根据维数公式 W 的 dim = V 的 dim ，因此 W = V。类似地，如果 W = V，则根据维数公式 K 的 dim = 0，因此 K = O。在这两种情况下，T 都是双射的。

(b) 当且仅当这两个条件 K ∩ W = {0} 和 K + W = V 都成立时，V 是直和 K ⨁ W 。若 K ∩ W = {0} = 0 ，则 K 和 W 是不相关的(相互独立的)，因此 U = K + W 是直和 K ⨁ W ，且 dim(U) + dim(K ) = dim(W ) ( 3.6.6 (a)) 。根据维数公式有 dim(U ) = dim(V ) ，因此 U = V ，这表明 V = K ⨁ W 。若 K + W = V ，则根据维数公式和 (3.6.6) (a)，有 K 和 W 是不相关的，同样，V 是直和。

• 满足条件 (4.3.1)(a) 的线性算子称为可逆算子(a invertible operator)。其逆函数也是线性算子。不可逆算子称为奇异算子(a singular operator)。

当 V 的维数为无穷大时，命题 4.3.1(a) 的条件不等价。例如，令 $V=\mathbb{R}^{\infty}$ 为无限维行向量 $(a_{1} , a_{2 },...)$ 的空间(见 3.7 节)。则右移(right shift)算子 $S^{+}$ 的核定义为

(4.3.2) $S^{+}(a_{1} , a_{2} ,...) = (0, a_{1} , a_{2} ,...)$ ，

这是一个零空间(zero space)，并且其像是V 的一个真子空间。左移算子 $S^{-1}$ 的核定义为

$S^{-}(a_{1} , a_{2} ,a_{3} ,...) = (a_{2} ,a_{3} ,... )$ ,

其是 V 的一个真子空间，其像是整个V 空间。

当我们处理线性算子时，上一节关于基的讨论必须略作修改。我们应该只为 V 选取一个基 B，并用它来代替 (4.2.6) 中的基 B 和 C (译注：因为线性算子是到其自射的映射)。换言之，为了定义 T 的相对于基 B 的矩阵 A，我们应该写成

(4.3.3) T(B) = BA 且 AX = Y 如前。

与任何线性变换(4.2.7)一样，A 的列是基向量的像 $T(v_{j})$ 的坐标向量：

(4.3.4) $T(v_{j}) = v_{1} a_{1j} + ... + v_{n} a_{nj }$

(译注： $T(v_{j})$ 应改为 T( v)，即对于线性空间中的任一向量 v ，可以用基向量的坐标向量表示。 )

当且仅当一个线性算子关于任意基的矩阵都是可逆矩阵时，此线性算子可逆。

当谈到空间 $F^{m}$ 上的线性算子的矩阵时，除非指定其他基，否则假设基为标准基 E。然后，该算子就是该基(向量)与该矩阵的乘法。

当我们研究基变换的影响时，就出现了一个新的特征。假设 B 被一个新的基 $\mathsf{B}^{'}$ 所取代。

命题 4.3.5 令 A 为一个线性算子 T 针对一个基 B 的矩阵。则

(a) 假设新的基 $\mathbf{B}^{'}$ 可表示为 $\mathbf{B}^{'}=\mathbf{B}P$ 。则 T 针这个基 $\mathbf{B}^{'}$ 的矩阵表示为 $A^{' }= P^{-1}AP$ 。

(b) 表示算子 T 对于不同基的矩阵 $A^{' }$ 是形如 $P^{-1}AP$ 的矩阵，其中P 可以是任意可逆矩阵。

换言之，矩阵按共轭(conjugation)改变。这是一个令人困惑且难以理解的事实。因此，尽管它遵循 (4.2.13)，但我们将重新推导它。由于 $\mathbf{B}^{'}=\mathbf{B}P$ 且由于 T(B) = BA ，我们有

$T(\mathbf{B}^{'}) = T(\mathbf{B}P) = \mathbf{B}PA = \mathbf{B}AP$

(译注：作者在这里默认矩阵乘法PA 可交换，否则不可这样写。)

这样我们还没有完成，我们已有的公式根据旧的基 B 表示 $T(\mathbf{B}^{'})$ 。为了获得新的矩阵，我们必须根据新的基 $\mathbf{B}^{'}$ 来记 $T(\mathbf{B}^{'})$ 。因此我们将 $\mathbf{B} = \mathbf{B} ^{'} P^{-1}$ 代入公式 (译注：根据 $\mathbf{B}^{'} = \mathbf{B}P$ ，两则右乘 $P^{-1}$ 即得到 B )。这样做就行到 $T(\mathbf{B}^{'}) = \mathbf{B}AP = \mathbf{B}^{'} P^{-1}AP = \mathbf{B}^{'} (P^{-1}AP )$ ，从而 $A^{'} = P^{-1}AP$ 。

通常，若一个方阵 A 与另一个方阵 $A^{'}$ 对于某个可逆矩阵 P 满足 $A^{'} = P^{-1}AP$ ，则我们此二矩阵是相似矩阵(similar)。这样的一个方阵 $A^{'}$ 可基于A 用 $P^{-1}$ 取共轭而得到。由于 P 可以是任意可逆矩阵，因此 $P^{-1}$ 也可以是任意可逆矩阵。用“共轭(conjugate)”代替“相似”是合适的。(译注：此处的所谓共轭是指矩阵 A 左乘 $P^{-1}$ 再右乘 P ，或左乘 P 再右乘 $P^{-1}$ ，A处于对称中心，符合共轭对称的思想。)

现在，如果已知矩阵 A ，很自然地会寻找一个特别简单的相似矩阵 $A^{'}$ 。人们希望得到类似定理 4.2.10 的结果。但在这里，我们允许的变化受到更多限制，因为我们只有一个基，因此只有一个矩阵 P 可用。线性变换的定义域和值域相等，乍一看似乎是一种简化，但实际上却使事情变得更加困难。

我们可以通过将假设的基变换矩阵写成基变换矩阵(basechange)的乘积来深入了解这个问题。例如，设 $P = E_{1} ... E_{r}$ 。则

$P^{-1}AP = E_{1}^{-1}...E_{r}^{-1} AP E_{1} ... E_{r}$ 。

就基本运算而言，我们可以通过一系列步骤 $A\rightsquigarrow E^{-1}AE$ 来改变 A (译注：符号 ⇝ 为右向花体(波浪箭头)，Unicode为“021DD”，LaTex 语法为 “\rightsquigarrow”)。换言之，我们可以对 A 执行任意列运算 E ，但我们还必须进行与逆矩阵 $E^{-1}$ 相对应的行运算。遗憾的是，这些行运算和列运算会相互作用，分析它们会变得令人困惑。

4.4 特征向量(Eigenvectors)

分析线性算子 T : V ⟶ V 的主要工具是不变子空间和特征向量。

• 对于 V 的一个子空间 W ，若其通过算子将其映射到自身，即

(4.4.1) TW ⊂ W ，

则称其为不变子空间(invariant (subspace))，或更确切地称为 T 不变子空间 。换言之，若只要 w 在 W 中，就有T(w) 也在 W 中，则 W 是不变的。这时，T 在 W 上定义了一个线性算子，称其为 W 的限制 (restriction)。我们通常将这个限制表示为 $T|_{W}$ 。

若 W 是一个 T 不变子空间，我们可以通过向 W 的一个基 $( w_{1} , ... , w_{k} )$ (译注：有的书上用 $\{ w_{1} , ..., w_{k} \}$ 表示一个基，其中 $w_{i}$ 是基中的线性无关向量)中追加向量以构成 V 的一个基 B ，比如

(4.4.2) $\mathbf{B} = (w_{1} ,... , w_{k}; v_{1} , ... , v_{n-k})$ 。

那么，W 的不变性这一事实反映在 T 的矩阵中。这个矩阵(我们称之为 M )的列是像向量之坐标向量(参见 (4.3.3))。但 $T(w_{j})$ 位于子空间 W 中(译注：应记为 T (w) )，因此它是基 $(w_{1} , ... , w_{k})$ 的线性组合。当我们用基 B 表示 $T(w_{j})$ 时(译注：应记为 T(w))，向量 $v_{1} ,... , v_{n-k}$ 的系数将为零。因此，M 具有分块形式

(4.4.3)

$\begin{bmatrix} A&B\\ 0&D\end{bmatrix}$ ，

其中，A 是 k × k 矩阵，即，T 对 W 的限制矩阵。

若 V 刚好是两个 T 不变子空间的直和 $W_{1}\oplus W_{2}$ ，且若我们追加 $W_{1}$ 和 $W_{2}$ 的基向量创建 V 的一个基 $\text{B} = ( \text{B}_{1} , \text{B}_{2} )$ ，则 T 的矩阵将具有对角块形式

(4.4.4)

$M=\begin{bmatrix} A_{1}&0\\ 0&A_{2}\end{bmatrix}$ ,

其中 $A_{i}$ 是 T 对 $W_{i}$ 的限制。

特征向量的概念与不变子空间的概念密切相关。

• 一个线性算子 T 的一个特征向量是一个非零向量，其使得对于某个标量 λ ，即对于某个 F 的元素，有

(4.4.5) $T(v) = \lambda {v}$ 。

如果一个非零列向量是方阵 A 左乘运算的特征向量，则该非零列向量是方阵 A 的特征向量。

在 (4.4.5) 中出现的标量 λ 称为与特征向量 v 关联的特征值(eigenvalue)。当我们提到线性算子 T 或矩阵 A 的特征值时，如果不指定特征向量，我们指的是与某个特征向量关联的标量 λ 。特征值可以是 F 中的任何元素(包括零)，但特征向量不能为零。特征值通常用希腊字母 λ(lambda)表示，就像这里一样。(注：德语单词“eigen”大致指的是英语中的“characteristic”。“Eigenvectors”和“eigenvalues”有时候称为特征向量(characteristic vectors)(译注：标量特为特征向量？这种解释不妥吧，还是分为特征向量和特征值较妥。))

具有特征值 1 的特征向量是一个固定的向量：T(v) = v 。一个具有特征值0 的特征向量位于零空间中：T(v) = 0 。(译注：特征值可以为0 ，特征向量不能为零。) 当 $V=\mathbb{R}^{n}$ 时，若一个非零向量 v 和线性变换 T(v) 是相似的(parallel)，则非零向量 v 是一个特征向量。

如果 v 是线性算子 T 的特征向量，其特征值为 λ，则 v 所构成的子空间 W 将是 T 不变的，因为 T(cv) = cλv，且对于所有标量 c，v 都在 W 中。反之，如果 v 所构成的一维子空间是不变的，则 v 是特征向量。因此，特征向量可以描述为一维不变子空间的基。

判断已知向量 X 是否为矩阵 A 的特征向量很容易。我们只需检查 AX 是否为 X 的倍数即可。若 A 是 T 关于基 B 的矩阵，X 是向量 v 的坐标向量，则当且仅当 v 是 T 的特征向量时，X 才是 A 的特征向量。

标准基 (列) 向量 $e_{1}=(1,0)^{t}$ 是矩阵

$\begin{bmatrix} 3&1\\ 0&2\end{bmatrix}$

的一个具有特征值 3 的特征向量，(列)向量 $(1,-1)^{t}$ 是另一个具有特征值 2 的特征向量。(列)向量 $(0,1,-1)^{t}$ 是矩阵

$A=\begin{bmatrix} 1&1&-1\\ 2&1&1\\ 3&0&2 \end{bmatrix}$

的特征值为 2 的特征向量。

若 $(v_{1} , ...,v_{n} )$ 是 V 的一个基，且若 $v_{1}$ 是一个线生算子 T 的一个特征向量，则 T 的矩阵具有块形式

(4.4.6)

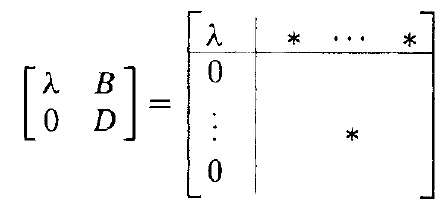
其中， λ 是 $v_{1}$ 的特征值。这是维度为 1 的不变子空间的块形式 (4.4.3)。

命题 4.4.7 相似矩阵 ( $A^{'} = P^{-1}AP$ ) 具有相同的特征值。

这是成立的，因为相似的矩阵代表相同的线性变换。

命题 4.4.8 (a) 令 T 为一个向量空间 V 上的线性算子。则对于 T 关于一个基 $\mathbf{B} = ( v_{1} , ... , v_{n} )$ 的矩阵而言，当且仅当每一个其基向量 $v_{j}$ 是一个特征向量时，此矩阵是对角化的。

(b) 对于一个 n × n 矩阵 A ，则当且仅当存在 $F^{n}$ 的一个由特征向量组成的基时，此矩阵与一个对角矩阵相似。

这可从矩阵 A 的定义推出(见(4.3.4))。若 $T(v_{j})=\lambda_{j}v_{j}$ , 则

(4.4.9)

$T(\text{B}) = ( v_{1} \lambda_{1} , ... , v_{n} \lambda_{n} ) = ( v_{1} , ... , v_{n} )=\begin{bmatrix}\lambda_{1} &\cdots& \\ \vdots&\ddots&\vdots\\ &\cdots&\lambda_{n} \end{bmatrix}$ 。

该命题表明，只要线性算子具有足够多的特征向量，我们就可以简单地用对角矩阵表示它。我们将在 4.5 节中看到，复向量空间中的每一个线性算子至少具有一个特征向量；在 4.6 节中，我们将看到大多数情况下存在一个特征向量基。但是实向量空间中的线性算子不必具有任何特征向量。例如，平面旋转角度 θ 不会将任何向量传递到平行平面，除非 θ 为 0 或 π。旋转矩阵 (4.2.2) 中 θ ≠O,π) 没有实数特征向量。

• 具有至少一个实特征值的实矩阵的一般示例是其所有元素均为正的矩阵。这样的矩阵称为正矩阵(positive matrices)，在实际应用中很常见，其最重要的性质之一是它们始终具有一个坐标为正的特征向量(即正特征向量)。

我们并不打算证明这一事实，而是通过考虑乘以一个基于 $\mathbb{R}^{2}$ 的正 2 × 2 矩阵 A

的效果来说明它。令 $w_{i} = Ae_{i}$ 为 A 的例。向量加法的平行四边(parallelogram)形法则表明，A 将第一象限 S 映射到由向量 $w_{1}$ 和 $w_{2}$ 所围成的扇形域。 $w_{i}$ 的坐标向量是矩阵 A 的第 i 列。由于矩阵A的项是正的，则向量 $w_{i}$ 位于第一象限。因此 A 将第一象限映射到其自身：S ⊃AS 。应用 A 于这个包含中，我们求得 $AS \supset A^{2}S$ ，如此等等：

(4.4.10) $S \supset AS \supset A^{2}S \supset A^{3}S\supset...$ ,

见如下以矩阵 $A=\begin{bmatrix} 3&2\\ 1&4\\ \end{bmatrix}$ 为例进行的说明。

现在，一个扇区的嵌入集的交集要么是一个扇区，要么是一条半线。在我们的案例中，交集 $Z = \cap A^{r}S$ 被证明是一条半线。这在直觉上是合理的，可通过各种方式证明，但我们忽略对其证明。我们在关系式 $Z = \cap A^{r}S$ 的两边乘以 A ：

$AZ=A \bigg (\bigcap_{0}^{\infty}A^{r}S \bigg )=\bigcap_{1}^{\infty}A^{r}S=Z$ 。

因此，AZ = Z 。因此，Z 的非零向量是特征向量。

(4.4.11)

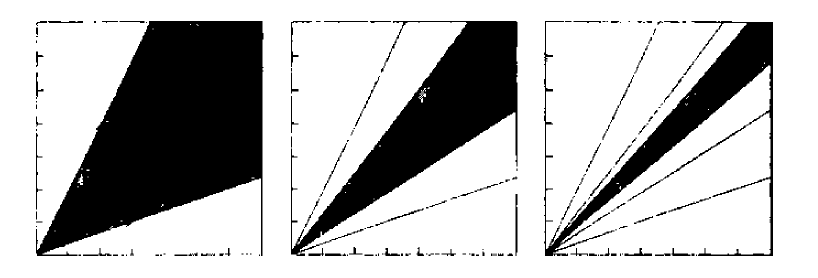
-----------------------------第一象限在正矩阵连乘下的像----------------------

4.5 特征多项式(The characteristic polynomial)

在本节中，我们确定任意线性算子的特征向量。我们记得，线性算子 T 的特征向量是一个非零向量 v，其对于F中的某个 λ ，满足

(4.5.1) T(v) = λv 。

如果不知道λ ，当算子矩阵较复杂时，直接求特征向量会很困难。诀窍在于解决另一个问题，即先确定特征值。一旦确定了特征值λ，公式(4.5.1)在v坐标系下就变为线性的，求解起来也就没有问题了。我们先将 (4.5.1)写成形式

(4.5.2) [λI – T ]( v) = 0 ，

其中，I 表示恒等算子，且 [λI – T ] 是一个线性算子，定义为

(4.5.3) [λI – T ]( v) = λv – T( v) 。

不难验证 λI – T 确为一个线性算子。我们可以将(4.5.2) 重述为：

(4.5.4) 对于一个非零向量 v ，当且仅当其位于 λI – T 的核中时，其是一个行征向量，且特征值为 λ 。

推论 4.5.5 令 T 为一个有限维向量空间 V 上的一个线性算子。

(a) T 的特征值是 F 中使得算子 λI – T 呈奇异性(即其零空间是非零的)的标量 λ 。

(b) 下述条件是等价的：

• T是奇异算子。

• T具有等于零的特征值。

• 若 A 是 T 关于任意一个基矩阵，则 det(A) = 0 。

(译注：det(行列式)(determinant 。)

若 A 是 T 关于某一个基的矩阵，则 λI – T 的矩阵是 λI – A 。因此，当且仅当 det(λI – A) = 0 时，λI – T 是奇异的。这个行列式可以用不确定的A来计算，这样做至少在原则上为我们提供了一种确定特征值和特征向量的方法。

假设(例如) A 是矩阵 $\begin{bmatrix} 3&2\\ 1&4\end{bmatrix}$ ，其在 $\mathbb{R}^{2}$ 上的行为如图 (4.4.11) 所示。则

$\lambda {I}-A = \begin{bmatrix} \lambda-3&-2\\ -1&\lambda-4 \end{bmatrix}$

和

$\det({\lambda}I - A) = \lambda^{2} - 7\lambda + 10 = (\lambda - 5)( \lambda - 2)$ 。

当 λ = 5 或 λ = 2 时此行列式消没，因此，A 的特征值是 5 或 5 。为了求得特征向量，我们解这两个方程组 [5I - A]X = 0 或 [2I - A]X = 0 。其解由标量因子确定：

(4.5.6) $v_{1}=\begin{bmatrix} 1\\ 1 \end{bmatrix}$ ， $v_{2}=\begin{bmatrix} 2\\ -1 \end{bmatrix}$ 。

现在我们考虑任意大小的不确定矩阵的相同计算。通常用变量 t 代替符号 λ。我们构造矩阵 tI – A ：

(4.5.7)

$tI - A = \begin{bmatrix} (t-a_{11})&-a_{12}&\cdots&-a_{1n}\\ -a_{21}&t-a_{22}&\cdots&-a_{2n} \\ \vdots&\vdots&\vdots&\vdots \\ -a_{n1}&\cdots&\cdots&-a_{nn} \\ \end{bmatrix}$ 。

行列式的完全展开式[第 1 章(1.6.4)]表明，det (tI – A) 是 t 中的 n 次多项式，其系数是标量，即 F 的元素。

定义 4.5.8(特征多项式之定义) 一个线性算子 T 的特征多项式是多项式

p( t ) = det (tI – A) ，

其中，A是线性算子 T 关于同一个基的矩阵。T 的特征值通过结合 (4.5.5)和(4.5.8)而确定：

推论 4.5.9 一个线性算子的特征值是其特征多项式的根。

推论 4.5.10 令 A 为具有对角项 $a_{11} ,..., a_{nn}$ 的上三角形矩阵或下三角形矩阵。则 A的特征多项式是 $(t - a_{11})...(t - a_{nn})$ 。A 的对角线项是其特征值。

证明：

若 A 是上三角矩阵，则 tI – A 也是上三角矩阵，tI – A 的对象项是 $t-a_{ii}$ 。三角矩阵的行列式是其对象项之积。

命题 4.5.11 一个线性算子的特征多项式与基的选择无关。

证明：

第二个项导出了一个矩阵 $A^{'} = P^{-1}AP$ (4.3.5) ，且

$tI - A^{'} = tI - P^{-1}AP = P^{-1}(tI - A)P$ 。则

$\det (tI - A^{'}) = \det P^{-1} \det(tI - A) \det(P) = \det(tI - A)$ 。

2 × 2 矩阵 $A=\begin{bmatrix} a&b\\ c&d\end{bmatrix}$ 的特征多项式是

(4.5.12)

$p(t) = \det(tI - A) = \det {\begin{bmatrix} t-a&-b\\ -c&t-d\end{bmatrix}}=t^{2}-(\text{trace}\;{A})t+(\det{A})$ ,

其中，trace A = a + d 。

下一个命题给出了 n × n 矩阵特征多项式的不完全描述，并通过计算得到证明。确定其余系数并不困难，但它们的显式公式并不常用。

命题 4.5.13 一个 n × n 矩阵 A 的特征多项式形如

$p(t) = \det(tI - A) = t^{n}-(\text{trace}\;{A})t^{n-1}+(-1)^{n}(\det{A})$ ，

其中，trace A (A 的迹) 是其对角项之和：

$\mathbf{trace} \;{A} = a_{11} + a_{22} + ... + a_{nn}$ 。

命题 4.5.1 表明，特征多项式的所有系数与基无关。例如， $\mathbf{trace}{(P^{-1}AP)}=\mathbf{trace}{\;A}$ 。

因为特征多项式，矩阵的迹，以及行列式与基无关，它们仅取决于算子T 。因此我们可以定义一个线性算子的相关项特征多项式，迹，和行列式。它们均可以利用 T 关于任意基的矩阵获得。

命题 4.5.14 令 T 为一个基于一个有限维向量空间 V 的线性算子。

(a) 若 V具有一个维数 n ，则 T 最多具有 n 个特征向量。

(b) 若 F 是复数域且 V ≠ 0 ，则 T 至少具有一个特征值，从而至少具有一个特征向量。

证明：

(a) 特征值是特征多项式的根，其具有次数 n 。一个n次多项式至多可以有n个根。这对于在任意域 F 中具有系数的多项式而方都是成立的(参见 (12.2.20))。

(b) 代数基本定理断言，每一个具有复系数的正产次数多项式都至少有一个复根，第15章(15.10.1)中存在这个定理的证明。

例如，令 $R_{\theta}$ 为表示穿过角度 θ 的 $\mathbb{R}^{2}$ 沿逆时针旋转的矩阵 (4.2.2) ，其特征多项式 $p(t) = t^{2} - 2t\cos(\theta) + 1$ 无实根(假设 θ ≠ 0，π) ，因此没有实特征值。在此之前我们已经注意到这一点。但由 $R_{\theta}$ 所定义的 $\mathbb{C}^{2}$ 上的算子确实具有复特征值 $e^{{\pm}i\theta}$ 。

注意：当我们谈论一个多项式 p(t)的根或一个矩阵或线性算子的特征特值时，都假设包括多个根的重复(repetitions)，这个术语尽管不是很精确，但却是很方便的。

推论 4.5.15 若 $\lambda_{1} ,... , \lambda_{n}$ 是一个 n × n 复矩阵 A 的特征值，则 det A 是乘积 $\lambda_{1} ,... , \lambda_{n}$ ，而 trace A 是和 $\lambda_{1} + ... + \lambda_{n}$ 。

证明：

令 p(t ) 为 A 的特征多项式。则

$(t - \lambda_{1})...(t - \lambda_{n}) = p(t) = t^{n} - (\mathbf{trace}\; A) t^{n-1} + ... \pm(\det {A})$ 。

4.6 三角形和对角形(Triangular and diagonal forms)

在本节中，我们将证明，基于复向量空间中的“大多数”线性算子，都存在一个基，使得算子的矩阵是对角的。关键事实(第 4.5 节末尾未提及)是，每一个正次数的复多项式都有一个根。这意味着每一个线性算子至少都有一个特征向量。

命题 4.6.1

(a) 向量空间形式：令 T 为一个基于一个有限维复向量空间 V 的线性算子。则存在 V的一个基 B ，使得 T 关于这个个基的矩阵是上三角矩阵。

(b) 矩阵形式：每一个复 n×n 矩阵 A 都相似于一个上三角矩阵：存在一个矩阵 $P\in GL_{n}(\mathbb{C})$ 使得 $P^{-1}AP$ 成为上三角矩阵。

证明：

根据 (4.3.5)，以上两个断言是等价的。我们将处理这个矩阵。令 $V=\mathbb{C}^{n}$ 。根据 4.5.14 (b) ，V 包含 A 的一个特征向量，不妨设其为 $v_{1}$ 。令 λ 为其对应的特征值。我们将(v)扩展为 V 的一个基。则新的矩阵 $A^{'}$ 具有块形式

(4.6.2)

$A^{'} = \left[ \begin{array}{c|c} \lambda & \ast \\ \hline 0 & D \end{array} \right]$ ，

其中，D 是一个 (n - 1)×(n - 1) 矩阵(见 (4.4.6) )。基于 n 做归纳，我们可以假设存在这样一个矩阵 $Q\in GL_{n-1}(\mathbb{C})$ ，其使得 $Q^{-1}AQ$ 为上三角矩阵，并且这个事实将会被证明。令

$Q_{1} = \left[ \begin{array}{c|c} 1 & 0\\ \hline 0 & Q \end{array} \right]$ 。则 $A^{''} = Q_{1}^{-1}A^{'}Q=\begin{bmatrix} \lambda&*\\0&Q^{-1}DQ \end{bmatrix}$ 是上三角矩阵，且 $A^{''} = (PQ_{1})^{-1}A(PQ_{1})$ 。

推论 4.6.3 在命题(4.6.1)中用短语“下三角矩阵”替代短语“上三角矩阵”，此命题仍然成立。

下三角矩阵形式可通过按相反的次序列出 (4.6.1)(a)的基 B 的形式得到。

命题 4.6.1 证明的重点在于每个复数多项式都有一个根。同样的证明适用于任何域 F，只要特征多项式的所有根都在该域中。

推论 4.6.4

(a) 向量空间形式：令 T 为一个基于一个域F上的有限维向量空间 V 的线性算子，且假设T的特征多项式是一个域 F 中的线性因式之积。则存在 V 的一个基 B，使得 T 的(关于这个基的)矩阵是上三角矩阵(或下三角矩阵)。

(b) 矩阵形式：令 A 为一个其项位于域 F 中的 n×n 矩阵，其特征多项式是线性因式之积。则存在一个矩阵 $P\in GL_{n}(F)$ 使得 $P^{-1}AP$ 成为上三角(或下三角)矩阵。

证明是相同的，只是为了进行归纳步骤，必须检查 (4.6.2) 中出现的矩阵 D 的特征多项式是否为 p(t)/( t - λ)，其中 p(t) 是 λ 的特征多项式。然后，特征多项式分解为线性因式的假设从 A 延续到 D 。

我们现在要问，哪些矩阵 A 与对角矩阵相似？它们称为可对角化矩阵。正如我们在 (4.4.8) (b) 中看到的那样，它们是以特征向量为基的矩阵。类似地，以特征向量为基的线性算子称为可对角化算子。对角线元素(它们的顺序除外)由线性算子 T 决定。它们是特征值。

下面的定理 4.6.6 对我们的问题给出了部分答案；下一节将给出更完整的答案。

定理 4.6.5 令 $v_{1} , ..., v_{r }$ 为一个线性算子T 的具有不同特值 $\lambda_{1} , ..., \lambda_{r }$ 的(r 个) 特征向量。则集合 $(v_{1} , ..., v_{r })$ 中的向量是线性无关的。

证明：

我们基于 r 做归纳证明。当 r = 1 时这个断言是成立的，因为一个特征向量不能为零。假设一个依赖关系

$0 = a_{1} v_{1} + ... + a_{r }v_{r}$

是已知的。我们必须证明对于所有的 i 有 $a_{i}=0$ 。我们应用线性算子 T ：

$0 = T(0) = a_{1}T(v_{1}) + ... + a_{r}T(v_{r}) = a_{1} \lambda_{1}v_{1} + ... + a_{r} \lambda_{r} v_{r}$ 。

这是 $(v_{1} , ..., v_{r })$ 之间的第二个依赖关系。我们从这两个关系消除 $a_{r}$ ，用 $\lambda_{r}$ 乘以第一个关系并减去第二个关系，得到：

$0 = a_{1}(\lambda_{r} - \lambda_{1})v_{1} + ... + a_{r-1}(\lambda_{r} - \lambda_{r-1})v_{r-1}$ 。

应用递归，我们可以假设 $(v_{1} , ..., v_{r-1 })$ 是一个线性无关集。这表明系数 $a_{i}(\lambda_r - \lambda_{i})(i < r)$ 均为零。由于 $\lambda_{i}$ 之间是不同的，则若 i < r 则 $\lambda_{r}-\lambda_{i}$ 不为零。因此， $a_{1} = ... = a_{r-1} = 0$ 。则原关系式将简化为 $0 = a_{r} v_{r}$ 。因为一个特征向量是不能为零的，因此 $a_{r}$ 必须为零。

结合 (4.4.8) 和 (4.6.5) 得到下一个定理：

定理 4.6.6 令 T 为一个基于一个域 F 上的 n 维向量空间 V 的线性算子。若其特征多项式在 F 中有 n 个不同的根，则存在一个 V 的基，使得 T 关于这个基的矩阵呈对角化。

注意：对象化是一个强大的工具。当遇到可对角化的算子时，应该会自动地运用特征向量的基。

作为对角化的一个例子，我们考虑实矩阵

(4.6.7) $A=\begin{bmatrix} 3&2\\ 1&4\end{bmatrix}$ 。

其特征向量计算见 (4.5.6)。这些特征向量构成了 $\mathbb{R}^{2}$ 的一个基 $\mathbf{B}=(v_{1},v_{2})$ 。根据 (3.5.13) ，将标准基 E 与基 B 关联起来的矩阵是

(4.6.8) $P=[\mathbf{B}]=\begin{bmatrix} 1&2\\ 1&-1\end{bmatrix}$ ， $P^{-1}=\frac{1}{3}\begin{bmatrix} 1&2\\ 1&-1\end{bmatrix}$ 且

(4.6.9) $P^{-1}AP=\frac{1}{3}\begin{bmatrix} 1&2\\ 1&-1\end{bmatrix}\begin{bmatrix} 3&2\\ 1&4\end{bmatrix}\begin{bmatrix} 1&2\\ 1&-1\end{bmatrix}=\begin{bmatrix} 5&\\&2\end{bmatrix}=A$ 。

下一个命题是命题 4.4.8 的变体。我们忽略其证明。

命题 4.6.10 令 F 为一个域。

(a) 令 T 为 $F^{n}$ 上的一个线性算子。若 $B = (v_{1} ,...,v_{n} )$ 是T 的一个特征向量的基，且若 P = [B] , 则 $\Lambda= P^{-1} AP = [B]^{-1} A[B]$ 呈对角化。

(b) 令 $\mathbf{B} = (v_{1} ,...,v_{n} )$ 为 $F^{n}$ 的一个基，并令 Λ 为具有对象项 $\lambda_1 , ... , \lambda_r$ (不必不同)的一个对角矩阵。则存在一个唯一的矩阵 A ，使得对于 i = 1, … ,n ， $v_{i}$ 都是 A 的一个具有特征值 $\lambda_{i}$ 的特征向量，即矩阵 $[\mathbf{B}]A [\mathbf{B}]^{-1}$ 。

记公式 $[\mathbf{B}]A [\mathbf{B}]^{-1}=\Lambda$ 的一个好方式是

(4.6.11) $A[\mathbf{B}]=\mathbf{B}\Lambda$ 。

定理 4.6.6 的一个应用是计算可对角化矩阵的幂。需要指出的是，只要展开公式的左边并消去 $PP^{-1}$ 即很容易得到下一个引理。

引理 4.6.12 令 A , B 和 P 分别为 n × n 矩阵。若 P 是可逆的，则 $(P^{-1}AP ) (P^{-1}BP ) = (P^{-1}(AB)P )$ ，且对于所有 k ≥ 1 ,有 $(P^{-1}AP )^{k}=(P^{-1}A^{k}P )$ 。

因此，若 A , P ，和 Λ 如 (4.6.9) 中所示，则

$A^{k}=P\Lambda P^{-1}=\frac{1}{3}\begin{bmatrix} 1&2\\ 1&-1\end{bmatrix}\begin{bmatrix} 5&\\&2\end{bmatrix}\begin{bmatrix} 1&2\\ 1&-1\end{bmatrix}=\\\\\\\\ \frac{1}{3}\begin{bmatrix} 5^{k}+2^{k+1}&2.5^{k}-5^{k+1}\\5^{k}-2^{k}&2.5^{k}+2^{k}\end{bmatrix}$ 。

若 $f (t) = a_{0} + a_{0}t +...+ a_{n} t^{n}$ 是一个以 t 为变量的其系数位于域 F 中的多项式(函数)，则 f (A) 表示在形式上用 A 代入 t 所得到的矩阵。即

(4.6.13) $f (A) = a_{0}I + a_{1}A + ... + a_{n} A^{n}$ 。

常量项 $a_{0}$ 用 $a_{0}I$ 代替。则若 $A = P\Lambda P^{-1}$ ，有

(4.6.14) $f (A) = f (P{\Lambda}P^{-1}) = a_{0}I + a_1 P{\Lambda}P^{-1} + ... + a_{n} P{\Lambda}^{n} P^{-1} = Pf ({\Lambda})P^{-1}$ 。

类似的符号也可用于线性算子：如果 T 是一个基于一个域 F 上的向量空间 V 的一个线性算子，则 V 上的线性算子 f (T )定义为

(4.6.15) $f (T) = a_{0}I + a_{1}T + ... + a_{n} T^{n}$ ，

其中， I 表示恒等算子，算子 f (T ) 作用于向量上则表示为 $f (T)v = a_{0}Iv + a_{1}Tv + ... + a_{n} T^{n}v$ 。(为了避免使用太多的括号，我们忽略了一些括号，记 T(v) 为 Tv 。)

4.7 Jordan形式(Jordan form)

假设已知一个有限维复向量空间 V 上的一个线性算子 T 。我们已经知道，如果其特征多项式的根不同，则存在一个特征向量基，并且 T 关于该基的矩阵是对角矩阵。这里我们想问，如果不假设特征值不同，可以做什么。当特征多项式有多个根时，通常不会有特征向量基，但我们将会看到，尽管如此，矩阵仍然可以变得相当简单。

一个线性算子 T 的具有特征值为 λ 的特征向量是一个非零向量 v，其满足 (T – λ )v = O 。( 这里我们将 T – λI 记为 T – λ 。) 由于算子 T 可能没有足够的特征向量，因此我们使用广义特征向量。

• 一个线性算子 T 的具有特征值为 λ 的广义特征向量是一个非零向量 x ，其使得对于某个 k > 0 有 $(T-\lambda)^{k}x=0$ 。其指数是使得 $(T-\lambda)^{d}x=0$ 的最小的整数 d 。

命题 4.7.1 令 x 为 T 的广义特征向量，其特征值为 λ 且指数为 d ，对于 j ≥ 0 , 令 $u_{j} = (T-\lambda)^{j} x$ 。令 $\mathbf{B} = ( u_{0} ,..., u_{d-1} )$ , 并令 X = Span B 。则 X 是一个T不变子空间，且 B 是 X 的一个基。

我们在证明中用到了下述引理。

引理 4.7.2 $u_{j}$ 如上所述，一个线性组合 $y = c_{j}u_{j} + ... + c_{d-1} u_{d-1}$ ( j ≤ d – 1 ， $c_{j} \neq 0$ ) 是一个广义特征向量，其特征值为 λ 且指数为 d – j 。

证明：

由于 x 的指数是 d ， $(T-\lambda)^{d-1}x=0=u_{d-1} \neq 0$ 。因此 $(T-\lambda)^{d-j-1}y=c_{j}u_{d-1}$ 不为零。但 $(T-\lambda)^{d-1}y=0$ 。因此，y 是一个广义特征向量，且特征值为 λ 且指数为 d– j ，正如断言所述。

命题 4.7.1 之证明：

我们注意到，

(4.7.3) $\left \{ \begin{array}{lrc} \lambda u_{j}+u_{j+1}\quad(\text{if} \quad j < d-1) \\ \\ \lambda u_{j} \quad (\text{if} \quad j = d-1) \\ \\ 0\quad(\text{if} \quad j > d-1) \end{array} \right.$

因此，对于所有的 j ， $Tu_{j}$ 都位于 X 的子空间中。这表明 X是不变量。接下来，根据定义，B 生成 X 。引理表明，B 的每一个非平凡线性组合都是广义特征向量，因此它不为零。因此，B 是一个独立集(译注：线性无关集)。

推论 4.7.4 令 x 为 T 的广义特征向量，特征值为 λ 。则 λ 是一个普通特征值——T 的特征多项式之根。

证明：

若 x 的指数是 d ，则按照如上记法， $u_{d-1}$ 就是一个具有特征值 λ 的特征向量。

公式 4.7.3 确定了描述 T 在命题 4.7.1 的基 B 上的行为的矩阵。它是一个 d × d Jordan 块矩阵 $J_{\lambda}$ 。较低 d 值的 Jordan 块矩阵如下所示：

(4.7.5) $J_{\lambda}=[\lambda]$ , $\begin{bmatrix} \lambda&\\1&\lambda\end{bmatrix}$ , $\begin{bmatrix} \lambda&\\ 1&\lambda& \\ &1&\lambda \end{bmatrix}$ ， $\begin{bmatrix} \lambda&\\ 1&\lambda& \\ &1&\lambda \\ &&1&\lambda \end{bmatrix}$ ，....

当 λ = 0 , Jordan 块的运算相当简单。基于 $\mathbb{C}^{d}$ 的一个标准确的 d × d 块 $J_{0}$ 的计算为

(4.7.6) $e_{1} \rightsquigarrow e_{2} \rightsquigarrow ...\rightsquigarrow e_{d }\rightsquigarrow 0$ 。

1 × 1 块Jordan 块 $J_{0}$ 是零。

下面的 Jordan 分解定理断言，任何复 n × n 矩阵都类似于由对角 Jordan 块(4.7.5) 组成的矩阵 J ——它具有 Jordan 形式

(4.7.7) $J=\begin{bmatrix} J_{1}&\\ &J_{1}& \\ &&\ddots \\ &&&J_{\ell} \end{bmatrix}$ ,

其中，对于某个 $\lambda_{i }$ ，有 $J_{i }=J_{\lambda_{i }}$ 。块 $J_{i }$ 具有各种大小 $d_{i}(\sum{d_{i}}=n)$ ，且对角项 $\lambda_{i}$ 不必相异。矩阵 J 的特征多项式是

(4.7.8) $p(t) = (t-\lambda_{1})^{d_{1}}(t-\lambda_2)^{d_{2}} ... (t-\lambda_\ell)^{d_{l}}$ 。

2 × 2 和 3 × 3 的 Jordan 形式是

(4.7.9) $\begin{bmatrix} \lambda_{1}&\\0&\lambda_{2}\end{bmatrix}$ ， $\begin{bmatrix} \lambda_{1}&\\1&\lambda_{2}\end{bmatrix}$ , $\begin{bmatrix} \lambda_{2}&\\ &\lambda_{2}& \\ &&\lambda_{2} \end{bmatrix}$ ， $\begin{bmatrix} \lambda_{2}&\\ 1&\lambda_{2}& \\ &&\lambda_{2} \end{bmatrix}$ ， $\begin{bmatrix} \lambda_{2}&\\ 1&\lambda_{2}& \\ &1&\lambda_{2} \end{bmatrix}$ 。

其中，标量 $\lambda_{i }$ 可以相等或不等，在第四个矩阵中，块可以按其它顺序列出。

定理 4.7.10 Jordan 分解定理。

(a) 向量空间形式：设 T 是一个有限维复向量空间 V 上的一个线性算子。则存在V的一个基 B ，使得 T 关于 B 的矩阵具有 Jordan形式 (4.7.7)。

(b) 矩阵形式：令 A 为一个 n × n 复矩阵。则存在一个可逆复矩阵 P ，使得 $P^{-1}AP$ 具有 Jordan形式。

同样，算子 T 或矩阵 A 的 Jordan 形式除了块的顺序外也是唯一的。

证明：

这个证明是Filippov提出的。我们基于对 V 的维数进行归纳证明，假设该定理对于 T任意真不变子空间的限制成立。因此，如果 V 是真 T 不变子空间的直和，比如 $V_{1}\oplus... \oplus V_{r} (r > 1)$ ，则对 T 而言这个定理是成立的。

假设我们已经推广了 $v_{i}$ (对于 i = 1 ,… ,r )。令 $V_{i}$ 为按命题 4.7.1 定义的子空间，且 $x=v_{i}$ 。若 V 是直和 $V_{1}\oplus... \oplus V_{r}$ ，则定理对于 V 成立，且我们称 $v_{1} ,...,v_{r}$ 是 T 的 Jordan 生成元(Jordan generators)。我们将证明存在一组 Jordan 生成元。

第1步：

我们选取 T 的一个特征值 λ，并将算子 T 替换为 T - λI。如果 A 是 T 关于某个基的矩阵，则 T - λI 关于同一基的矩阵将是 A - λI；如果 λ 或 A - λI 中的一个矩阵是Jordan式，则另一个也是Jordan式。因此，用 T — λI 替换 T 是可以的。这样做之后，我们的算子(我们仍称之为 T )的特征值将为零。这将简化符号。

第2步：

我们假设 0 是 T 的一个特征值。令 $K_{i}$ 和 $U_{i}$ 分别表示第 i 个幂 $T_{i}$ 的核和像。则 $K_{1} \subset K_{2} \subset ...$ 和 $U_{1} \supset U_{2} \supset ...$ 。因为 V 是有限维的，则对于大的 r ，这些子空间链变得固定，比如 $K_{m} = K_{m+1} = ...$ 和 $U_{m} = U_{m+1} = ...$ 。令 $K = K_{m}$ 和 $U =U_{m}$ 。我们验证 K 和 U 是不变子空间，且 V 是直和 K ⨁ U 。

这个子空间是不变的，因为 $TK_{m} \subset K_{m-1}\subset K_{m}$ 且 $TU_{m} = U_{m-1} = U_{m }$ 。为了证明 V = K ⨁U ，只需证明 K ∩U = { 0 } 即可(见命题 (4.3.1)(b))。令 z 为 K ∩U 的一个元素。则 $T^{m}z=0$ , 同样对于 V 中的某个 v 有 $T^{m}v=0$ 有 $z=T^{m}v$ 。从而 $T^{2m}v=0$ ，因此 v 是 $K_{2m}$ 的一个元素。但 $K_{2m} = K_{m}$ ，因此 $T^{m}v=0$ ，即 z = 0 。

由于 T 的特征值是 0，K 不是零子空间。因此 U 的维数小于 V ，根据我们的归纳假设，该定理对 $T|_{K}$ 成立。遗憾的是，我们不能将这个推理应用于 K，因为 U 可能为零。所以我们仍然必须证明 $T|_{K}$ 存在 Jordan 形式。我们将 V 替换为 K，将 T 替换为 $T|_{K}$ 。

• 对于一个基于一个向量空间 V 的线性算子 T , 若对于某个正整数 r ，算子 $T^{r}$ 为零，则称其为幂零算子(nilpotent operator)。

我们已经将证明简化为幂零算子的情况。

第3步：

我们假设算子 T 是幂零的。每一个非零向量都是一个特征值为 0 的广义特征向量。令 N 和 W 分别表示 T 的核和像。由于 T 是幂零的，所以 N ≠ {O}。因此 W 的维数小于 V 的维数，根据归纳法，该定理对于W 的算子限制情况成立。因此，存在 $T|_{W}$ 的Jordan 生成元 $w_{1},...,w_{r }$ 。令 $e_{i}$ 表示 $w_{i}$ 的指数，且令 $W_{i}$ 表示如命题 4.7.1 中那样使用广义特征向量 $w_{i}$ 所构成的子空间。因此 $W = W_{1}\oplus... \oplus W_{r}$ 。

对于每一个 i ，我们选择 V 的一个元素 $v_{i}$ ，使得 $Tv_{i}=w_{i}$ 。则 $v_{i}$ 的指数 $d_{i}$ 将等于 $e_{i}+1$ 。令 $V_{i}$ 表示如命题 4.7.1 中那样使用广义特征向量 $v_{i}$ 所构成的子空间。则 $TV_{i}=V_{i}$ 。令 U 表示和 $V_{1} + ... + V_{r}$ 。由于每一个 $V_{i}$ 都是一个不变子空间，因此 U 也是一个不变子空间。现在我们验证 $v_{1} ,...,v_{r}$ 是约束 $T|_{U}$ 的 Jordan 生成元。即子空间 $V_{i}$ 的向量是线性无关的。

我们注意到两件事：首先，TU = W ，因为 $TV_{i} = W_{i}$ 。第二， $V_{i}\cap N \subset W_{i}$ 。这可从引理 4.7.2 推导出，这表明 $V_{i}\cap N$ 是最后一个基向量 $T^{d_{i-1}}v_{i}$ 的张成(span)。因为 $d_{i-1} = e_{i}$ 是正的，因此 $T^{d_{i-1}}v_{i}$ 在像 $W_{i}$ 中。

我们假设已知一个关系 $\widetilde{v}_{1}+...+\widetilde{v}_{r}=0$ 且 $\widetilde{v}_{i}$ 位于 $V_{i}$ 中。我们必须证明 $\widetilde{v}_{i}=0$ (对于所有的 i )。令 $\widetilde{w}_{i}=T\widetilde{v}_{i}=0$ 。则 $\widetilde{w}_{1}+...+\widetilde{w}_{r}=0$ 且 $\widetilde{w}_{i}$ 位于 $W_{i}$ 中。因此子空间 $W_{i}$ 是线性无关的，因此对于所有 i 有 $\widetilde{w}_{i}=0$ 。从而 $T\widetilde{v}_{i}=0$ , 这意味着 $\widetilde{v}_{i}$ 位于 $V_{i}\cap N$ 中。因此 $\widetilde{v}_{i}$ 位于 $W_{i}$ 中。再次利用子空间 $W_{i}$ 是线性无关的事实，我们推断出对于所有 i 有 $\widetilde{v}_{i}=0$ 。

第4步：

我们证明，为了获得 T 的一组生成元，我们可以将 N 的某些元素加入到 $T|_{U}$ 的Jordan 生成元集 $\{ v_{1} ,...,v_{r} \}$ 中。

令 v 为 V 的任意一个元素，并令 Tv = w 。由于 TU = W ，则在 U 中存在一个向量 u ，使得 Tu = w = Tv 。则 z = v – u 位于 N 中，且 v = u + z 。因此，U + N = V 。既然如此，我们通过增加元素的方式(比如，加入 N 的元素 $z_{1} ,.... , z_{\ell}$ ) 将 U 的一个基扩展至 V 的一个基(见命题 3.4.16(a))。令 $N^{'}$ 为 $\{z_{1} ,.... , z_{\ell}\}$ 的一个张成。则 $U\cap N^{'}=\{0\}$ 且 $U+N^{'}=V$ ，因此，V 是直和 $U \oplus N^{'}$ 。

算子 T 在 $N^{'}$ 上是零。因此， $N^{'}$ 是一个不变子空间，且 $T|_{N^{'}}$ 的矩阵是零矩阵，其具有 Jordan 形式。其 Jordan 块是 1 × 1 零矩阵。从而 $\{ v_{1} ,... ,v_{r} ; z_{1} ,.. , z_{\ell} \}$ 是一组 T 的 Jordan 生成元。

只要已知特征值，且分析能证明形式的唯一性，确定算子 T 的若尔当形式并不困难。然而，求得 V 的合适基可能很费劲，最好避免。

为了确定 Jordan 形，我们选择一个特征值 λ ，并用 T — λI 替换 T ，从而将问题简化为 λ = 0 的这种情况。令 $K_{i}$ 表示 $T_{i}$ 的核，并令 $k_{i}$ 为 $K_{i}$ 的维数。在具有 λ = 0 的单个 d × d Jordan 块的情况下，这些维数是：

$k_{i}^{block}=\left \{ \begin{array}{rlc}i\quad (\text{if} \; i \leq d) \\ \\ d\quad (\text{if} \; i \geq d) \end{array} \right .$ 。

一个一般算子 T 的维数 $k_{i}$ 可通过向 λ = 0 的每一个块加入数 $k_{i}^{block}$ 而得到。因此， $k_{1}$ 将是具有 λ = 0 的块的数量， $k_{2}-k_{1}$ 将是具有 λ = 0 的大小为 d ≥ 0 的块的数量，如此等等。

两个简单的例子：

$A=\begin{bmatrix} 0&1&0\\ 1&0&1\\0 &-1&0 \end{bmatrix}$ 和 $B =\begin{bmatrix} 1&-1&1\\ 2&-2&2\\-1&1&-1 \end{bmatrix}$ 。

这里， $A^{3}=0$ ，但 $A^{2}\neq 0$ 。若 v 是一个使得 $A^{2}v\neq 0$ 的向量，比如说 $v=e_{1}$ ，则 $( v ,Tv , T^{2}v )$ 是一个基，这个 Jordan 形由一个单 3 × 3 块构成。

在另一方面， $B^{2}=0$ 。再次取 $v=e_{1}$ ，则集合 (v , Tv ) 是线性无关的，这就给出了一个 2 × 2 块。为了获得 Jordan 形，我们必须在 N 中加入一个向量，例如， $v^{'} = e_{2} + e_{3}$ ，这就给出 1 × 1 块(等于零) 。这是所求的基 $(v , Tv , v^{'} )$ 。

将 Jordan 形式写为 J = D + N 通常很有用，其中 D 是矩阵的对角线部分，N 是对角线下方的部分。对于单个 Jordan 块，我们将有 D = λI 和 $N=J_{0}$ ，如下图 3 × 3 块所示：

$J_{\lambda}=\begin{bmatrix} \lambda&\\ 1&\lambda& \\ &1&\lambda \end{bmatrix}=\begin{bmatrix} \lambda&\\ 0&\lambda& \\ &0&\lambda \end{bmatrix}+\begin{bmatrix} 0&\\ 1&0& \\ &1&0 \end{bmatrix}=\lambda{I}+J_{0}=D+N$ 。

记为 J = D + N 很方便，因为 D 与 N 可交换。J 的幂可以通过二项式展开式计算：

(4.7.11)

$J^{r} = (D + N)^{r} = D^{r} +\begin{pmatrix}r\\1\end{pmatrix}D^{r-1}N+\begin{pmatrix}r\\2\end{pmatrix}D^{r-2}N^{2}+...$ ,

当 J 是一个 n × n 矩阵时， $N^{r}=0$ ，这个展式具有至少 n 项。在一个单块的情况下，此公式读为

(4.7.12) $J^{r} = (\lambda{I} + J_{0})^{r} = {\lambda}^{r}{I} +\begin{pmatrix}r\\1\end{pmatrix}{\lambda}^{r-1}J_{0}+\begin{pmatrix}r\\2\end{pmatrix}{\lambda}^{r-2}{J_{0}}^{2}+...$ ,

推论 4.7.13 设 T 是一个有限维复向量空间上的一个线性算子。则以下条件是等价的：

(a) T 是可对角化的算子；

(b) 每一个广义特征向量都是特征向量；

证明：

(a) ⟹ (b)：假设 T 是可对角化算子，比如, T 关于基 $\mathbf{B}= (v_{1} ,...,v_{n})$ 的矩阵是具有对角项 ${\lambda}_1 ,... , {\lambda}_{n}$ 的对角矩阵 Λ 。令 v 为 V 中的一个广义特征向量，比如，对于某个 λ 和某个 k > 0 ， $(T-\lambda)^{k}v = 0$ 。我们用 T – λ 来代替 T 并简化为 $T^{r}v = 0$ 这种情况。令 $X = (x_{1} ,... ,x_{n} )^{t}$ 为 v 的坐标向量。则 $T^{k}v$ 的坐标将是 $\lambda_{i}^{k} x_{i}$ 。由于 $T^{k}v = 0$ ，则 $\lambda_{i}=0$ 或 $x_{i} = 0$ ，且在任一情况下，都有 $\lambda_{i}^{k} x_{i} = 0$ 。从而 Tv = 0 。

(b) ⟹ (c): 我们证明逆否命题。如果 T 的 Jordan 形式有一个 k × k Jordan 块，其中k > 1，那么回顾 $J_{\lambda} -{\lambda} I$ 的作用 (4.7.6)，我们发现存在一个广义特征向量，它不是特征向量。因此，如果 (c) 为假，则 (b) 也为假。最后，显然 (c) ⟹ (a)。

以下是 Jordan 形式的一个很好的应用。

定理4.7.14 设T 是一个有限维复向量空间V上的一个线性算子，如果T的某个正幂是恒等式，比如 $T^{t}=I$ ，则T 是可对角化的。

证明：

只需证明每一个广义特征向量都是一个特征向量即可。为此，我们假设 $(T- {\lambda}I )^{2}v = 0$ 且 v ≠ 0，并证明 (T - λ)v = 0。由于 λ 是特征值，且 $T^{r}=I$ ，因此 ${\lambda}^{r}=1$ 。我们将多项式 $t^{r}-1$ 除以 t - λ：

$t^{r} - 1 = (t^{r-1} + {\lambda}t^{r-2} + ... + {\lambda}^{r-2}t + {\lambda}^{r-1})(t - {\lambda})$ 。

我们将 t 替换为 T 并应用算子于 v 。令 w = (t - λ)v 。由于 $T^{r}-I = 0$ ,

$\begin{array}{rlc} 0 &= (T^{r} - I)v = (T^{r-1} + {\lambda}T^{r-2} + ... + {\lambda}^{r-2} T + {\lambda}^{r-1})( T - {\lambda})v \\\\ &= (T^{r-1} + {\lambda}T^{r-2} + ... + {\lambda}^{r-2} T + {\lambda}^{r-1})w \\\\ &= r{\lambda}^{r-1}w \end{array}$ 。