1) 深入剖析：核心方法与图示（Figure）逐一对应

1.1 单点三维提示的任务设定（Figure 1）

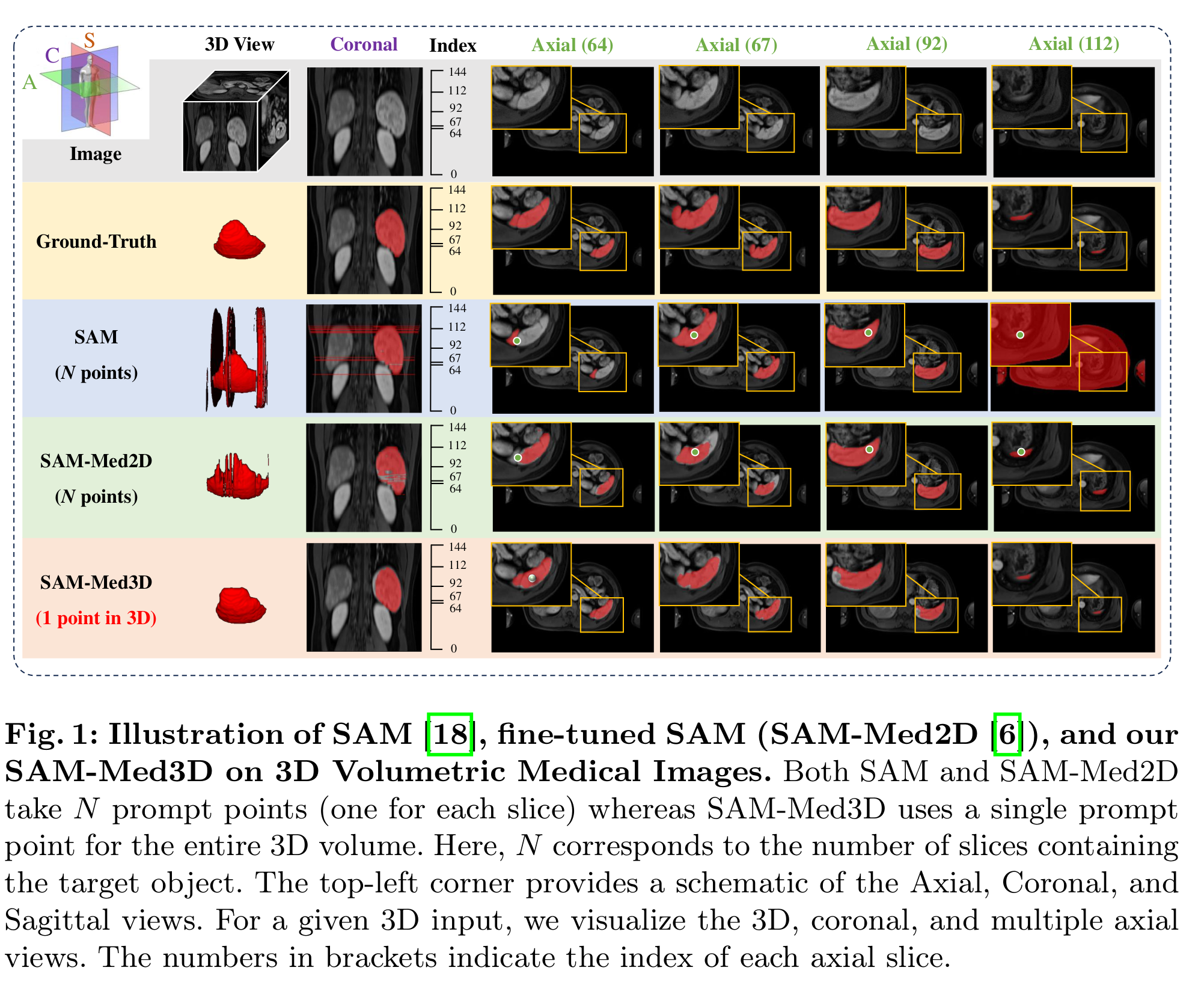
论文首先将3D交互式分割的提示形式从“2D逐片（每片1点，共N点）”切换为“体素级单点（1个3D点）”。Figure 1直观对比了 SAM（2D）/SAM-Med2D 与 SAM-Med3D（1点/体） 的差异：前两者对体数据需 N 个逐片点，而 SAM-Med3D 对整卷仅需一个三维点，显著减少交互负担。
图中还标注了轴位/冠状/矢状多视角展示，强调体素级提示对整体三维空间一致性的正向作用。

1.2 训练数据与规模（Figure 2）

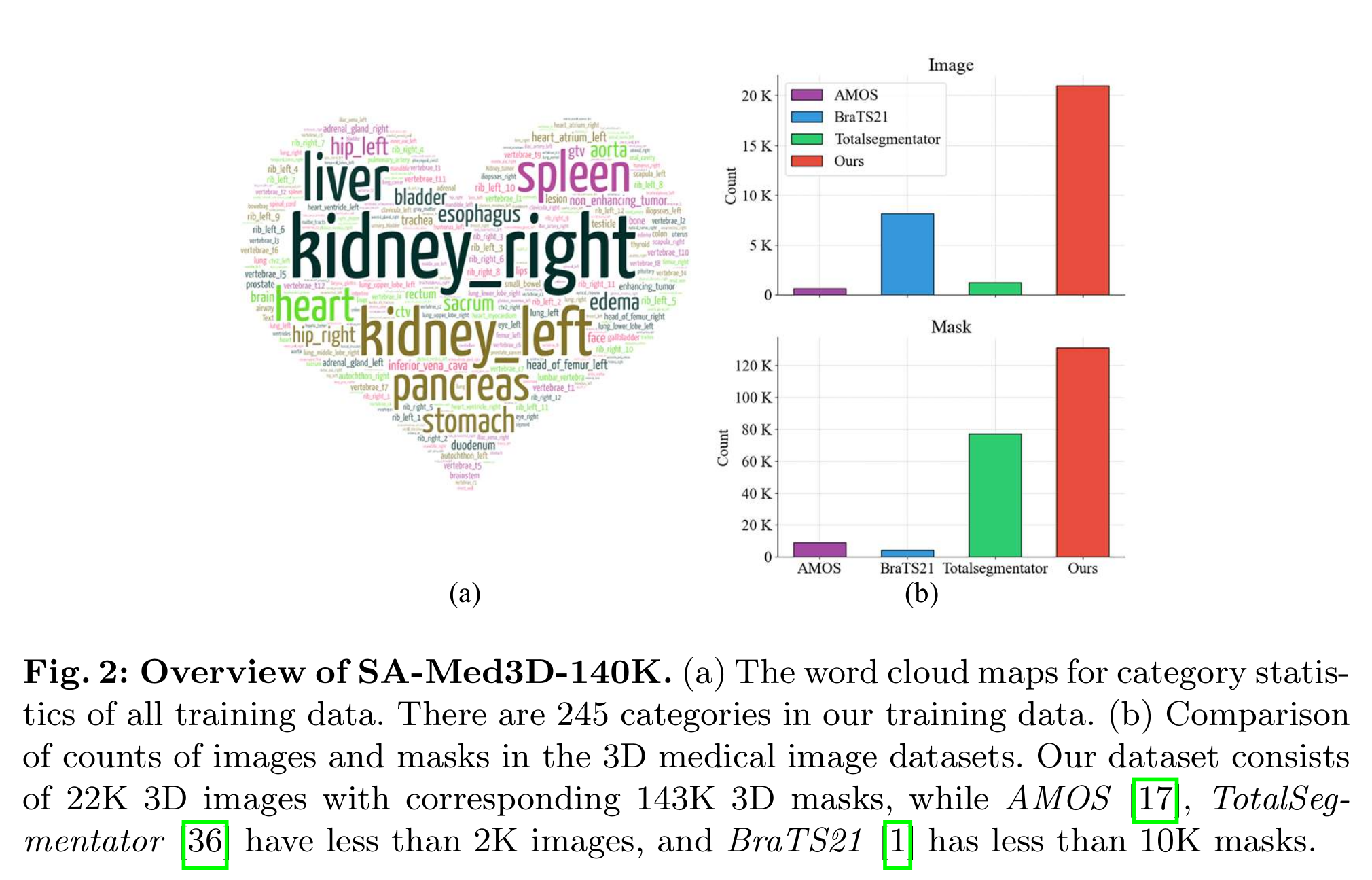
为支撑“通用型”能力，作者构建了 SA-Med3D-140K：共 22K 体数据、143K 3D mask、245 类别，来源于 70 个公开与 24 个私有数据集（并辅以清洗与歧义消解流程；见图中流程与词云示意）。
Figure 2(b) 对比了该数据与 AMOS、TotalSegmentator、BraTS 等常用集的数量级差异，凸显其“大而全”的覆盖面。

1.3 端到端纯三维架构（Figure 3）

Figure 3 给出了 SAM-Med3D 的三维化 ViT 架构：由 3D 图像编码器、3D 提示编码器、3D 掩码解码器三部分组成，并在各处使用 3D 绝对位置编码（3D Abs PE）、3D 多头自注意力（MSA）、3D MLP / 3D LayerNorm / 3D Conv 等三维算子，以原生三维方式建模体空间关系。

3D 图像编码器：将 [H, W, D] 体数据分块嵌入后，经堆叠的 3D 自注意力 + 3D MLP 模块提取三维上下文特征（图中“3D Attention Block”“Transformer Block×2”“3D MLP×2”等标注）。
3D 提示编码器：把 3D 点 (x,y,z) 编为提示向量，配合 Q/K/V 与 3D 相对/绝对位置编码，使提示与体特征在三维空间对齐（图中“3D Rel/Abs PE”“Q K V”“Prompt Embeddings”）。
3D 掩码解码器：接收图像/提示特征，输出体素级 mask（图中“3D Mask Decoder / Mask / Prediction”），完成少点交互→三维掩码的映射。
设计动机：作者比较了三种将 SAM 迁移到3D的方式（逐片聚合；2D主干+3D adapter；纯3D从头训练）。表2 的预实验结论是：adapter 在“