目录
基础的指令
format
矩阵和向量
找出某行某列的矩阵元素
快速打出多个矩阵或者向量
矩阵连接
矩阵计算
一些特殊矩阵fuction
矩阵相关函数
基础的指令
- clc
- 清空命令行窗口

- clear all
- 清空工作区的全部变量
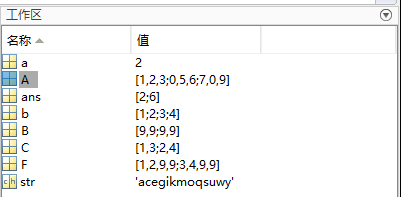
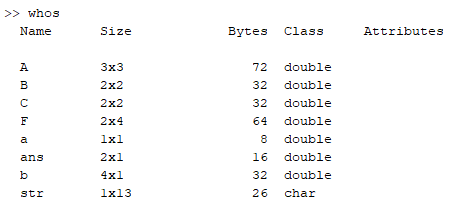
- who
- 将工作区的全部变量显示出来
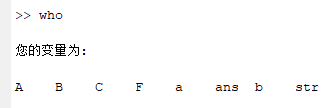
- whos
- 工作区的变量信息详细显示出来
format
format 默认格式
- format short 5字长定点数,显示5位(scaled fixed point format with 5 digits)
- format long 15字长定点数,显示15位双精度,7位单精度(scaled fixed point)
- format short e 5字长浮点数
- format long e 15字长浮点数
- format hex 16进制
- format bank 定点货币形式
- format rat 小数分数表示
- format + +,-,空格
- format compact 压缩空格
- format loose 包括空格和空行
- format long 15字长定点数
- format short e 5字长浮点数
- format long e 15字长浮点数
- format short g 5位定点或浮点格式。
- format long g 对双精度,显示15位定点或浮点格式,对单精度,显示7位定点或浮点格式
矩阵和向量
找出某行某列的矩阵元素
A = [1 21 6;5 17 9;31 2 7]
%如果我想把21打出来
%方法1-行+列
A(1,2)
%方法2-从上往下按列进行数
A(4)删除A的最后一行
A(3,:) = [ ]
快速打出多个矩阵或者向量
%% 快速打多个向量或者矩阵
%j:k--[j,j+1,j+2,...,j+m]
%j:i:k--[j,j+i.j+2*i...,j+m*i]
B = 1:5
B = 1:2:5
B = [1:5;2:3:15;-2:0.5:0]
str = 'a':2:'z'代码运行结果:

矩阵连接
A = [1 2;3 4]
B = [9 9;9 9]
F = [A B]%把A跟B加在一起变成一个增广矩阵代码运行结果:

矩阵计算
%% 矩阵计算
%+ - * / ^ 。 ' .*./ /->A*inv(B)
A+B
A-B
A*B
A.*B
A./B
a = 2;
A + 2
A/a
A./a
A
A^a
A.^a
C=A'一些特殊矩阵fuction
%% 特殊矩阵some specila matrix
%linspace() 线性间隔
%eye(n):nxn
%zeros(n1,n2):n1*n2 zero matrix
%ones(n1,n2):n1xn2 matrix with every entry as 1
%diag():diagonal matrix
%rand():uniformly distrubuted random numbers均匀分布的随机数
linspace(0,13,6)矩阵相关函数
%% some matrix related fuctions:一些和矩阵相关的函数
A = [1 2 3;0 5 6;7 0 9]
max(A)%7 5 9
max(max(A))sum(A)
mean(A)sort(A)%按列向量从小排到大
sortrows(A)%从第一列进行对比,把整行进行排序(整行绑定)
length(A)%长度
find(A==0)运行结果:
A =1 2 30 5 67 0 9
ans =7 5 9
ans =9
ans =8 7 18
ans =2.6667 2.3333 6.0000
ans =0 0 31 2 67 5 9
ans =0 5 61 2 37 0 9
ans =3
ans =26
——静态方法)

)
)







评测与实操:5 秒在线抠图、支持批量与换底(电商/设计团队提效指南))




 (三))
)
)