一、实验

在本节中，我们通过多个真实数据集和应用对所提出的方法进行评估。实验结果表明，相较于基线方法，该方法取得了显著提升。

1.1 数据集

为全面评估表征方法的有效性，实验采用五个网络数据集，包括三个社交网络、一个引文网络和一个语言网络，覆盖三种实际应用场景：多标签分类、链接预测及可视化。根据各数据集特性，针对每类应用选取一个或多个数据集进行性能评估，具体描述如下。

BLOGCATALOG [27]、FLICKR [27] 和 YOUTUBE [28]：它们是线上用户的社交网络。每个用户至少被标注为一个类别。BLOGCATALOG 共有 39 个不同类别，FLICKR 有 195 个类别，YOUTUBE 有 47 个类别。这些类别可作为每个顶点的真实标签，因此可用于多标签分类任务的评估。
ARXIV GR-QC [16]：这是一个论文合作网络，涵盖 arXiv 中广义相对论和量子宇宙学领域的论文。在该网络中，顶点代表作者，边表示作者曾在 arXiv 上合作撰写过科学论文。由于缺乏顶点类别信息，该数据集用于链接预测任务。
20-NEWSGROUP：该数据集包含约 20000 篇新闻组文档，每篇文档被标记为 20 个不同组别之一。使用词项的 TF-IDF 向量表示文档，并以余弦相似度衡量文档间相似性。基于此类相似性可构建网络。选取标注为 comp.graphics、rec.sport.baseball 和 talk.politics.guns 的文档进行可视化任务。

在加权与无权、稀疏与密集、小型与大型网络上进行实验，所选数据集能全面反映网络嵌入方法的特性。具体统计数据见表2。

1.2 基线算法

以下五种方法作为基线算法，其中前四种为网络嵌入方法，而共同邻居（Common Neighbor）直接基于网络结构进行链路预测，已被证明是有效的链路预测方法[17]。

DeepWalk [21]：采用随机游走和skip-gram模型生成网络表示。
LINE [26]：通过分别定义损失函数保留一阶或二阶近似性，优化后拼接不同阶数的表示。
GraRep [4]：扩展至高阶近似性，利用奇异值分解（SVD）训练模型，并直接拼接一阶与高阶表示。
拉普拉斯特征映射（LE）[1]：通过分解邻接矩阵的拉普拉斯矩阵生成网络表示，仅利用一阶近似性保留网络结构。
共同邻居[17]：仅通过顶点间共同邻居的数量衡量相似性，仅在链路预测任务中作为基线。

1.3 评估指标

在实验中，针对重构、链接预测、多标签分类和可视化任务，采用以下评估方法：
重构与链接预测任务使用precision@k和**平均精度均值（MAP）**进行评估，具体定义如下：

precision@k：该指标对返回结果中的每个实例赋予相同权重，计算公式为：

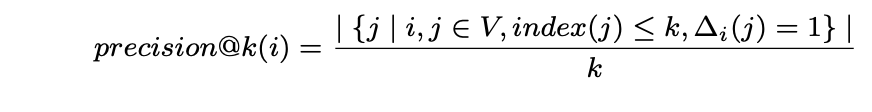
其中，V 为顶点集合，index(j) 表示第j个顶点的排序索引，∆i(j) = 1 用于标识顶点vi与vj之间存在连边关系。

Mean Average Precision (MAP) 是一种具有良好区分度和稳定性的评价指标。相较于 precision@k，它更关注返回结果中靠前排序项的表现。其计算方法如下：

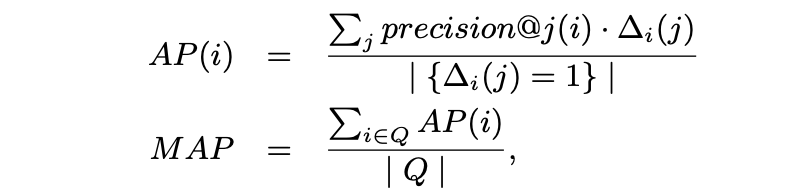
其中 Q 表示查询集

在多标签分类任务中，采用与许多其他研究相同的微平均F1（Micro-F1）和宏平均F1（Macro-F1）作为评估指标[27]。具体而言，对于标签A，用TP(A)、FP(A)和FN(A)分别表示被预测为A的实例中的真正例、假正例和假反例数量。设C为全体标签集合，微平均F1和宏平均F1定义如下：

Macro-F1 是一种给予每个类别同等权重的评估指标，其定义如下：

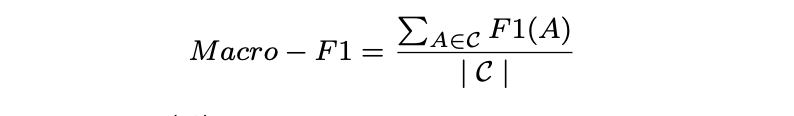
F1(A) 是标签 A 的 F1 值（F1 分数）

Micro-F1 是一种对每个实例赋予同等权重的评估指标，其定义如下：

1.4 参数设置

本文提出了一种多层深度结构，层数随数据集不同而变化。各层维度如表3所示。对于BLOGCATALOG、ARXIV GR-QC和20-NEWSGROUP数据集，神经网络设置为三层；对于FLICKR和YOUTUBE数据集，则使用四层结构。若采用更深的模型，性能几乎保持不变甚至可能下降。

方法参数设置

本方法的超参数α、β和ν通过网格搜索在验证集上进行调优。基线方法的参数均调整为最优值。

LINE参数配置

随机梯度下降（SGD）的迷你批次大小设为1，初始学习率为0.025。负采样数量设置为5，总样本数为100亿。依据文献[26]的建议，LINE模型的最终嵌入向量通过拼接一阶和二阶表示并做L2归一化后效果更佳，实验中遵循此方式生成LINE的结果。

DeepWalk参数配置

窗口大小设为10，随机游走长度设为40，每个顶点的游走次数设为40。

GraRep参数配置

矩阵转移步数最大值设为5。

1.5 实验效果

本节首先评估模型的重建性能，随后分析不同嵌入方法生成的网络表征在以下三类经典数据挖掘与机器学习任务中的泛化能力：多标签分类、链接预测及可视化。

1.5.1 网络重构

在评估所提方法在现实应用中的泛化能力之前，需对不同网络嵌入方法的网络重构能力进行基础评估。此实验的意义在于，优秀的网络嵌入方法应确保学习到的嵌入向量能够保留原始网络结构。实验选取语言网络ARXIV GR-QC和社交网络BLOGCATALOG作为代表案例。给定一个网络，分别使用不同嵌入方法学习网络表示，进而预测原始网络的链接。由于原始网络中的现有链接可作为真实标签，通过计算训练集误差即可评估各方法的重构性能。采用precision@k和MAP作为评估指标，precision@k结果如图3所示，MAP结果见表4。

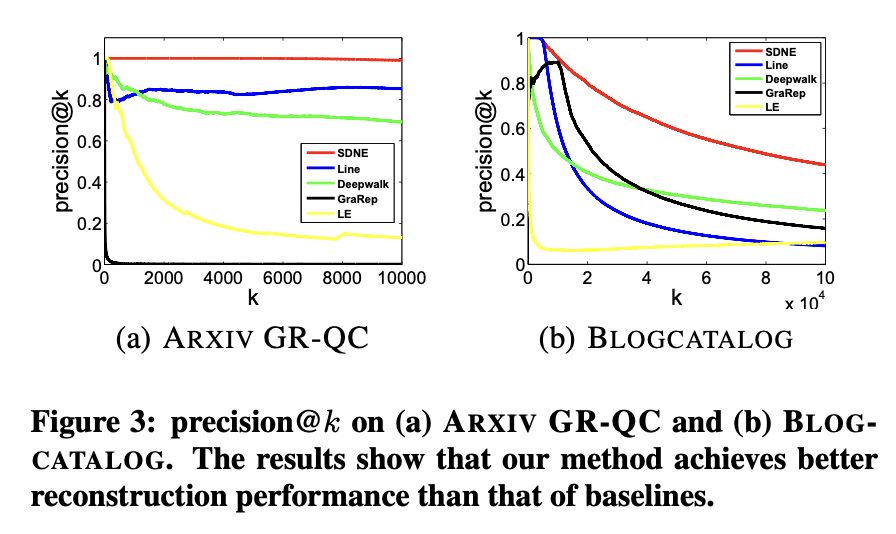
根据研究结果，可得出以下观察与分析：

1.5.1.1 方法性能优势

表4数据显示，该方法在两个数据集的MAP指标上均显著超越基线模型。图3表明随着k值增大，该方法的precision@k始终维持最高水平，证明该方法能有效保持网络结构完整性。

1.5.1.2 特定数据集表现

在ARXIV GR-QC网络中，该方法的precision@k可达100%并在k增至10000时保持该水平。考虑到该数据集总链接数为28980，说明该方法能近乎完美地重构原始网络结构。

1.5.1.3 模型对比分析

尽管SDNE和LINE均利用一阶与二阶邻近性保持网络结构，但SDNE表现更优。可能原因包括：LINE采用的浅层结构难以捕捉底层网络高度非线性特征；LINE直接拼接两种邻近性的表征方式，不如SDNE联合优化策略高效。

1.5.1.4 邻近性重要性验证

SDNE和LINE性能均优于仅使用一阶邻近性的LE算法，证明引入二阶邻近性可显著提升网络结构保持效果。

1.5.2 多标签分类

分类是众多应用中的核心任务，相关算法和理论已被大量研究[18]。本实验通过多标签分类任务评估不同网络表征方法的有效性。网络嵌入方法生成的顶点表征作为特征，用于将每个顶点分类至一组标签中。

具体采用LIBLINEAR工具包[8]训练分类器。训练时，随机抽取部分已标注节点作为训练数据，其余作为测试集。对于BLOGCATALOG数据集，随机选取10%至90%的顶点作为训练样本，剩余顶点用于测试性能；对于FLICKR和YOUTUBE数据集，则随机抽取1%至10%的顶点作为训练样本，剩余部分用于测试。此外，YOUTUBE数据集中未标注任何类别的顶点被移除。

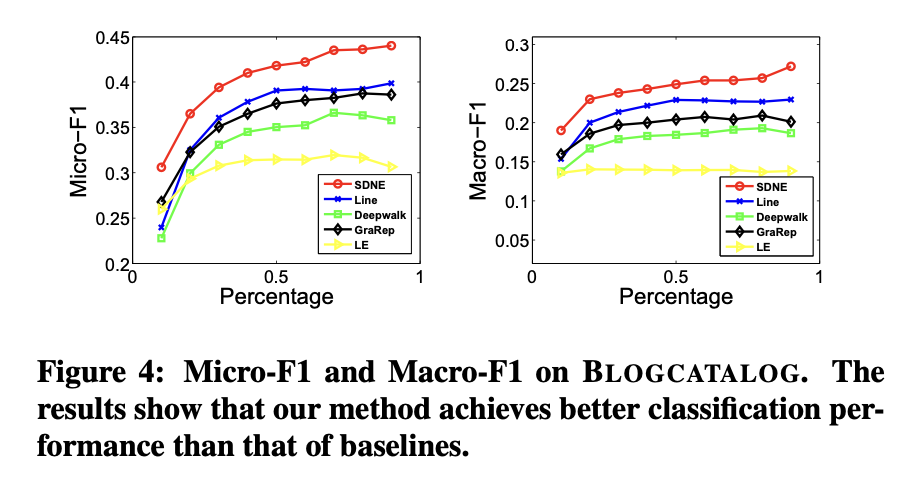
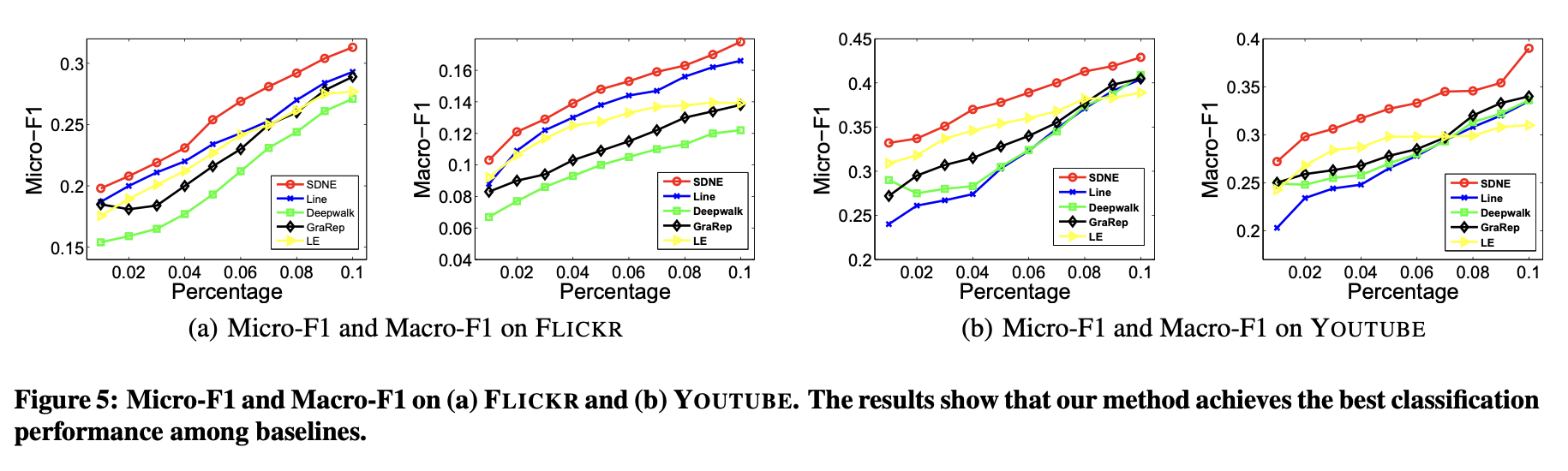
上述过程重复5次，最终报告平均Micro-F1和Macro-F1值。结果分别展示在图4与图5中。

关键点说明

数据划分：不同数据集的训练集比例差异（BLOGCATALOG较高，FLICKR/YOUTUBE较低）反映数据规模或标注密度的差异。
评估指标：Micro-F1（侧重全局统计）和Macro-F1（侧重类别均衡）共同衡量分类性能。
去噪处理：YOUTUBE中未标注顶点的剔除确保评估有效性。

在图表4与图表5中，本方法的曲线始终高于基线方法。这表明相比基线方法，本方法学习到的网络表征能更有效地泛化至分类任务。

图表4（BLOGCATALOG数据集）显示，当训练数据比例从60%降至10%时，本方法相对于基线方法的性能提升幅度更为显著。这说明在标注数据有限的情况下，本方法能实现更显著的性能优势。这一特性对实际应用尤为重要，因为真实场景中的标注数据通常稀缺。

在多数情况下，DeepWalk在网络嵌入方法中表现最差。原因有二：其一，DeepWalk缺乏明确的目标函数来捕捉网络结构；其二，该方法通过随机游走扩充顶点邻居关系，这种随机性会引入大量噪声（尤其对高度数顶点影响显著）。

1.5.3 链路预测

本节聚焦链路预测任务并开展两项实验：第一项评估整体性能，第二项分析网络稀疏性对不同方法性能的影响。实验数据集采用ARXIV GR-QC。

链路预测任务通过随机隐藏部分已有边，利用剩余网络训练嵌入模型。训练完成后获取顶点表示，进而预测未被观测的边。与重构任务不同，此任务旨在预测未来可能的连接而非还原现有边，因此能更好评估不同网络嵌入方法的可预测性性能。实验中引入共同邻居（Common Neighbor）作为基线方法，因其已被证明是有效的链路预测策略[17]。

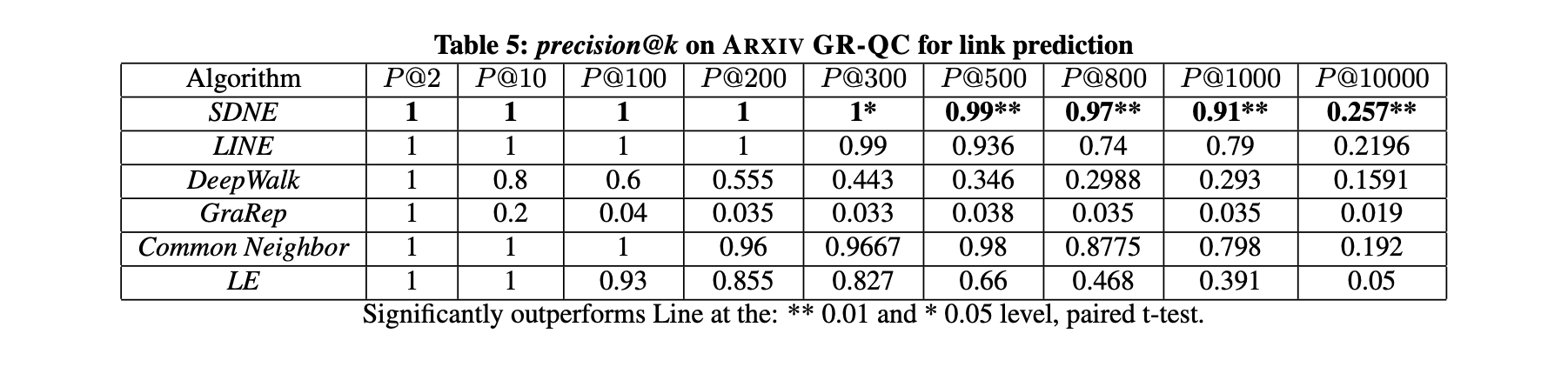
第一项实验随机隐藏15%的现有边（约4000条），采用precision@k作为预测隐藏边的评估指标。将k值从2逐步增至10000，结果如表5所示（最优性能以加粗标出）。表5的主要观察与分析如下：

结果表明，随着k值增大，本方法的性能始终优于其他网络嵌入方法。这表明本方法学习到的表征对新链接形成的预测能力更为出色。
当k=1000时，本方法的精度仍保持在0.9以上，而其他方法的精度迅速降至0.8以下。这说明本方法在排名靠前的链接中能保持较高精度。这一优势对推荐系统和信息检索等实际应用尤为重要，因为用户更关注此类应用中排名靠前的结果。

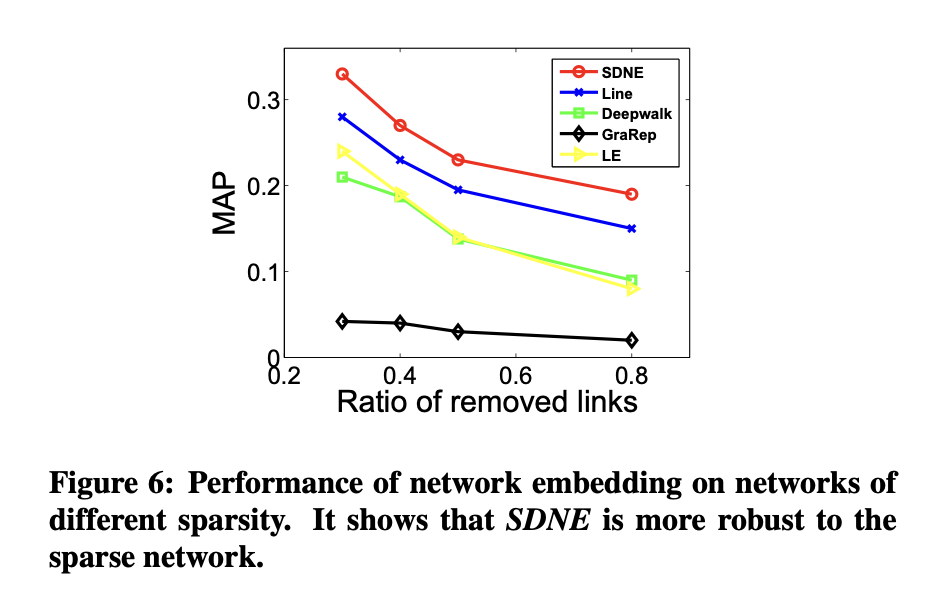
在第二个实验中，通过随机移除原始网络中的部分连接来改变网络的稀疏性，随后沿用前述流程比较不同网络嵌入方法的表现。结果如图6所示。

稀疏性对方法性能的影响

实验表明，当网络越稀疏时，拉普拉斯特征映射（LE）与SDNE、或LE与LINE之间的性能差距会进一步扩大。这说明引入二阶邻近度能够使学习到的表征对稀疏网络更具鲁棒性。

极端稀疏场景下的表现

即使移除80%的网络连接，SDNE方法仍显著优于基线模型。这一结果进一步验证了SDNE在处理稀疏网络时的强大能力。

1.5.4网络可视化的应用

网络嵌入的另一重要应用是在二维空间中生成网络的可视化。因此，此处对20-NEWSGROUP网络学习到的表征进行可视化呈现。采用不同网络嵌入方法学习到的低维网络表征作为可视化工具t-SNE的输入数据。每个新闻组文档被映射为一个二维向量，进而以二维空间中的点呈现。针对不同类别的标注文档，其对应点使用不同颜色标记。理想的可视化结果应表现为同色标记点彼此临近。可视化效果如图7所示。

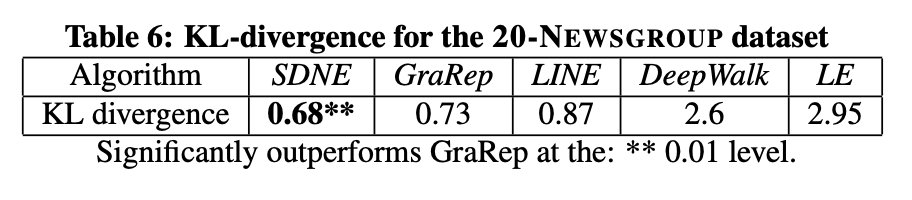
从图7可以看出，LE和DeepWalk的表现不尽如人意，因为不同类别的数据点相互混杂。LINE方法形成了不同类别的簇群，但在中心区域，不同类别的文档仍然存在重叠。GraRep的结果相对较好，相同颜色的点形成了独立的分组，但各组边界仍不够清晰。显然，SDNE在类群分离度和边界清晰度两方面的可视化效果最佳。表6的量化数据也进一步验证了该方法在可视化任务中的优越性。

1.6 参数敏感性分析

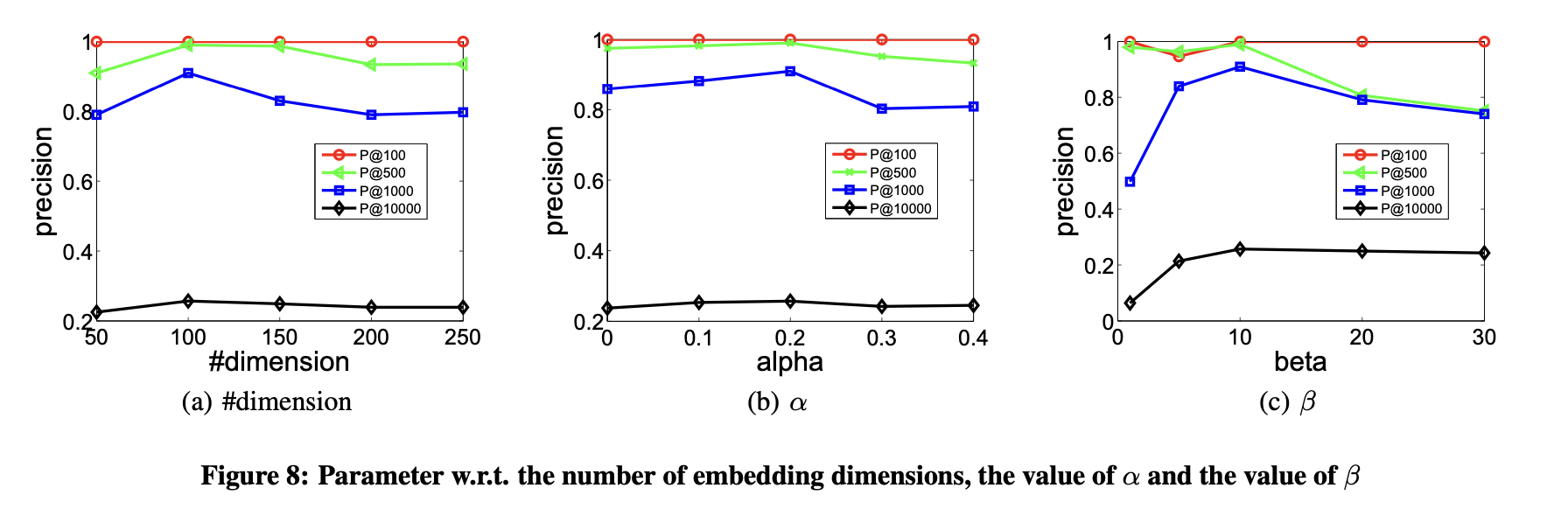
本节探讨参数敏感性问题，重点评估嵌入维度数量及超参数α、β取值对结果的影响。实验数据基于ARXIV-GRQC数据集，以Precision@k作为评价指标。

嵌入维度数量的选择

图8(a)展示了嵌入向量维度对性能的影响。性能随维度增加提升，因更多维度能编码更丰富的信息。但当维度持续增加时，性能缓慢下降，原因是过高的维度会引入噪声导致性能劣化。总体而言，潜在嵌入空间的维度数量需谨慎确定，但本方法对该参数不敏感。

一阶与二阶邻近性的平衡点分析

研究通过图8(b)展示了参数α对模型性能的影响。α用于调节顶点间一阶邻近性与二阶邻近性的权重比例。当α=0时，性能完全由二阶邻近性决定；随着α增大，模型更侧重一阶邻近性。图8(b)显示，α=0.1和α=0.2的性能优于α=0，表明同时考虑一阶和二阶邻近性对网络嵌入方法捕捉网络结构至关重要。该结果验证了两种邻近性在表征网络拓扑时的互补性。

重点关注非零元素的重构误差

实验最后展示了参数β对模型性能的影响。β控制训练图中非零元素的重构权重，其值越大，模型越倾向于优先重构非零元素。图8(c)结果显示：当β=1时效果较差，此时模型对网络中零元素和非零元素赋予同等重构权重。需注意的是，节点间无连边并不代表两者不相似，但存在连边一定表明节点相似性，因此重构零元素会引入噪声并降低性能。

过度强调非零元素的弊端

当β值过大时，性能同样会下降。原因是模型几乎完全忽略零元素的重构，倾向于维持任意节点对的相似性。然而，大量零元素实际仍反映节点间的差异性，过度忽略会导致性能退化。

实验结论

该实验表明：在网络嵌入任务中，应更关注非零元素的重构误差，但不可完全放弃对零元素的重构约束。需在二者间取得平衡以获得最优表现。

二、结论

本文提出了一种结构深度网络嵌入方法（Structural Deep Network Embedding, SDNE），用于实现网络嵌入。该方法通过设计半监督深度模型（含多层非线性函数）捕捉高度非线性的网络结构。为解决结构保持与稀疏性问题，模型联合利用一阶邻近度与二阶邻近度刻画局部与全局网络结构特征。通过在半监督深度模型中联合优化这两类邻近度，所学表征能够保持局部-全局结构，并对稀疏网络具有鲁棒性。实验部分在多个网络数据集和应用场景中评估了生成的网络表征效果，结果表明该方法较现有最优技术有显著提升。未来工作将聚焦于如何为无任何边连接的新节点学习表征。

本篇论文讲解就暂告一断落，后续会持续更新～