大家好，今天是 2025 年 9 月 11 日，我来给大家写一篇关于第十六届蓝桥杯软件赛 C 组省赛的C++ 题解，希望对大家有所帮助！！！

创作不易，别忘了一键三连

题目一：数位倍数

题目链接：数位倍数

【题目描述】

【算法原理】

签到题、枚举、数位拆分

只需要暴力枚举 1 到 202504 之间的所有整数，对于每一个整数，拆分它的每一位求和之后看看是不是 5 的倍数就可以了。

至于如何拆分一个整数的每一位，相信大家已经掌握的非常熟练了，直接来看代码。

【代码实现】

#include <iostream>using namespace std;bool check(int x)
{int sum = 0; // 统计每一个数的数位和while(x){sum += x % 10;x /= 10;}return sum % 5 == 0;
}int main()
{int cnt = 0;for(int i = 1; i <= 202504; i++)if(check(i))cnt++;cout << cnt << endl; return 0;
} 

题目二：2025

题目链接：2025

【题目描述】

【算法原理】

签到题、枚举、数位拆分

和题目一类似，只需要暴力枚举 1 到 20250412 之间的所有整数，对于每一个整数，拆分它的每一位并统计，之后看看是不是含有至少 1 个 0，2 个 2，1 个 5 就可以了。

至于如何拆分一个整数的每一位，相信大家已经掌握的非常熟练了，直接来看代码。

【代码实现】

#include <iostream>
#include <cstring>using namespace std;int cnt[10]; // cnt[i] 表示 i 这个数字出现了多少次bool check(int x)
{memset(cnt, 0, sizeof cnt);while(x){cnt[x % 10]++;x /= 10;}if(cnt[0] < 1 || cnt[2] < 2 || cnt[5] < 1) return false; return true;
}int main()
{int c = 0;for(int i = 1; i <= 20250412; i++)if(check(i))c++;cout << c << endl; return 0;
}

题目三：2025图形

题目链接：2025图形

【题目描述】

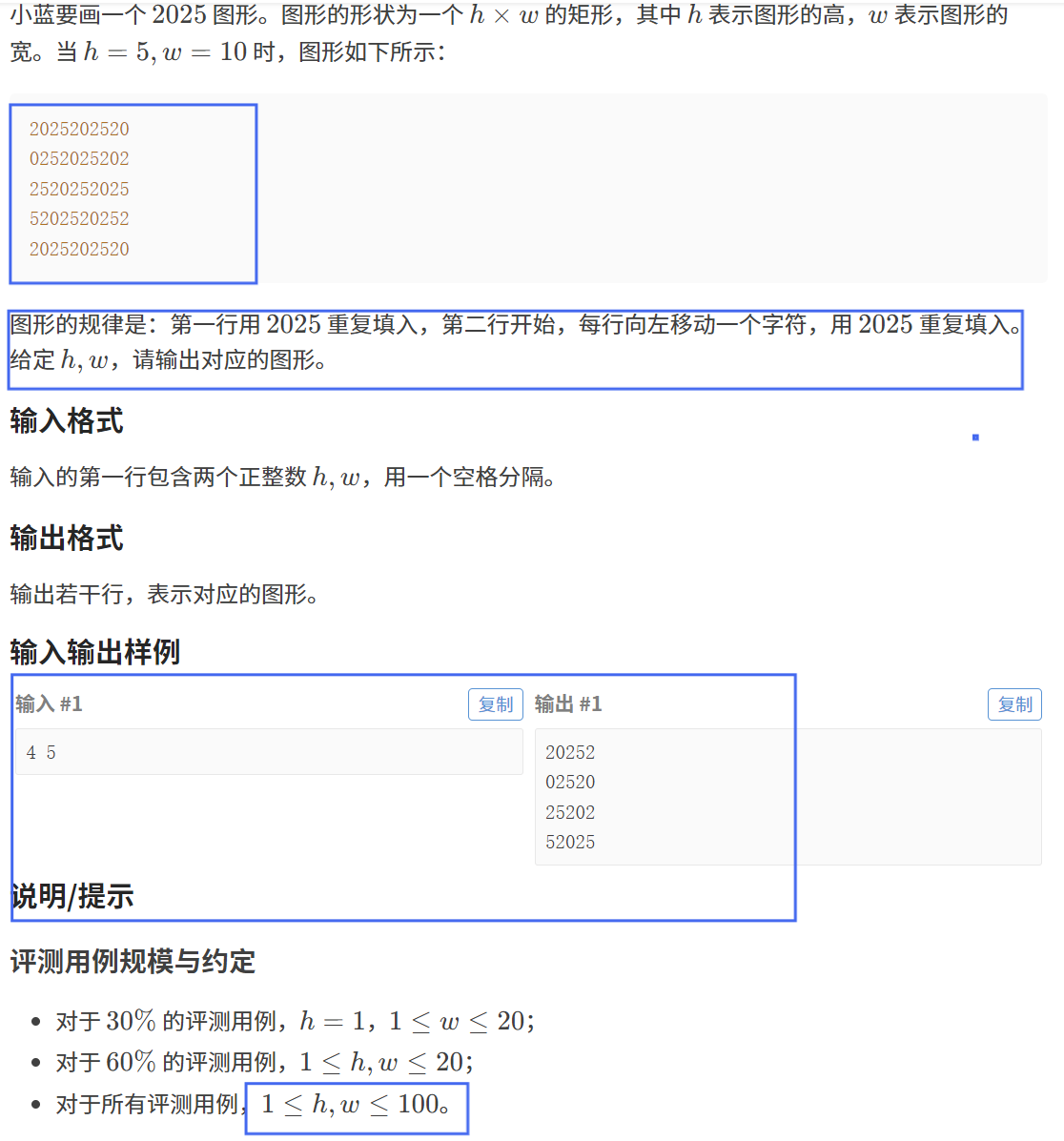
【算法原理】

签到题、模拟、取模运算

找规律 + 周期问题

这道题数据范围很小，我们完全可以首先构造出一个含有 200 个 “2025” 的字符串，然后针对每一行从不同的位置开始输出 w 个字符就可以了。（代码可以自己尝试实现）

但是，这样玩的话就没有什么意思了。我们能不能只存一个 “2025” 呢？

我们写几行找一找规律：

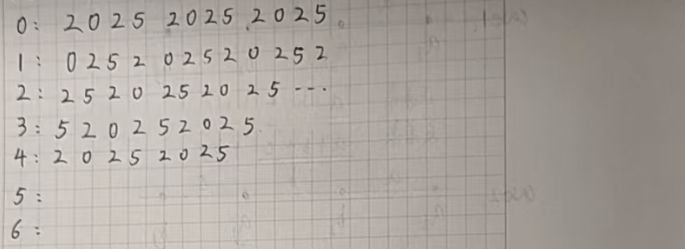
遇到周期问题，我们就要首先想到取模操作。

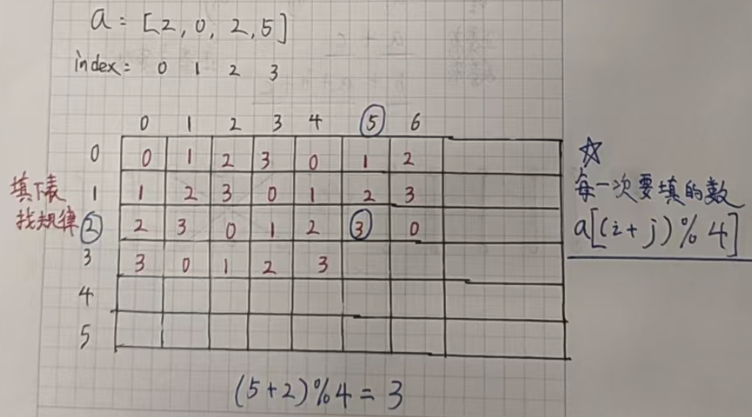
不难发现，这道题输出位置的值的下标就是横坐标的值和纵坐标的值之和再模四。

因此，这道题的规律我们就找到了，直接来看代码：

【代码实现】

#include <iostream>using namespace std;int a[4] = {2, 0, 2, 5};int main()
{int h, w; cin >> h >> w;for(int i = 0; i < h; i++){for(int j = 0; j < w; j++){cout << a[(i + j) % 4];} cout << endl;}return 0;
} 

题目四：最短距离

题目链接：最短距离

【题目描述】

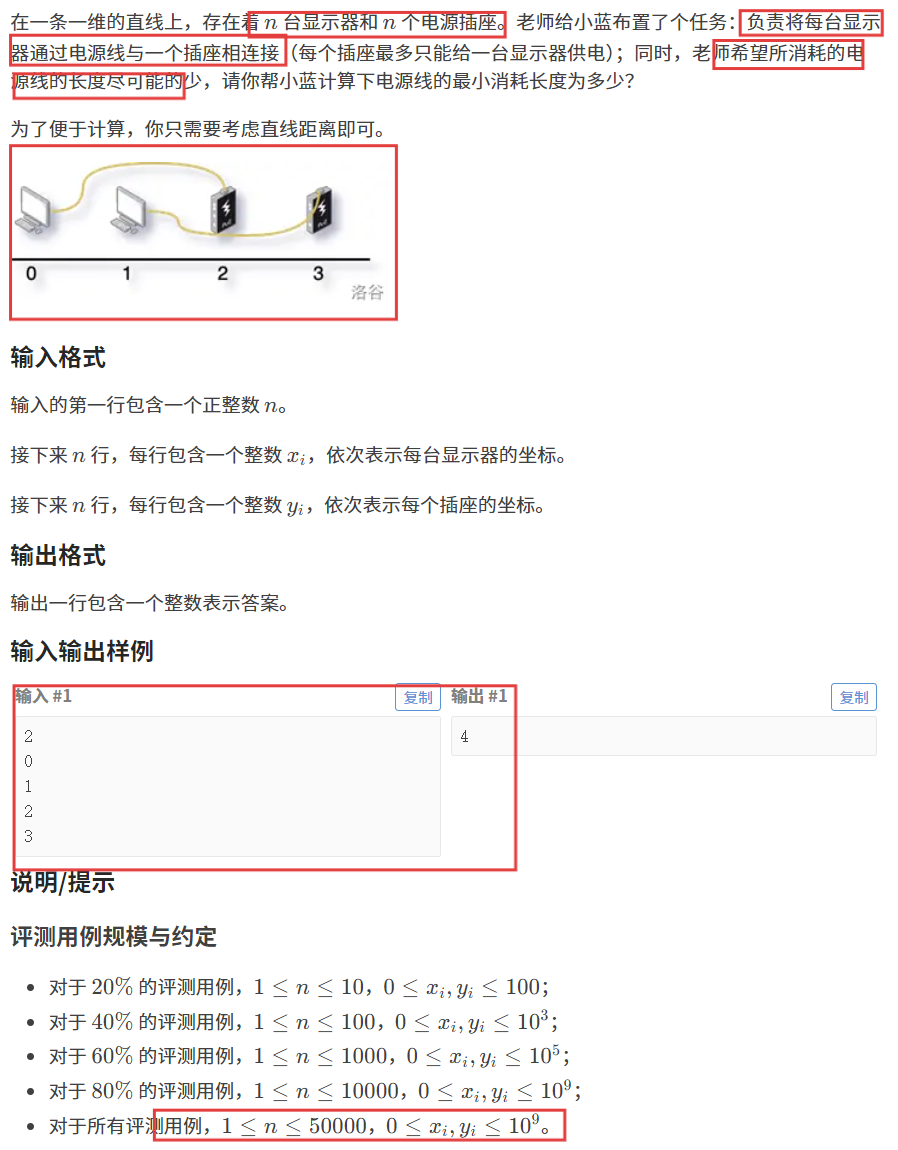
【算法原理】

贪心

这道题目一定不要一直拘泥于题目中的那一幅图当中，我们抛开坐标系不谈，其实这道题目就是让两个数组中的值一一对应，使得每一组差的绝对值之和最小：

（我当时就盯着题目中的那幅图在坐标系中想了很长时间）

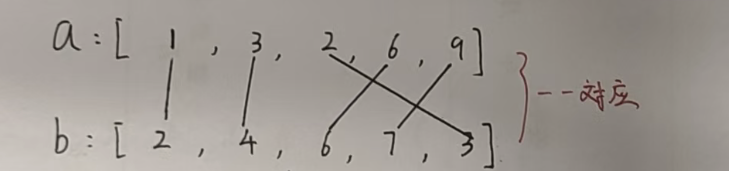
我们很容易想到一个贪心策略，就是将两个数组排序之后，然后按照从小到大的顺序一一对应就可以了。

（大家如果之前接触过这一类贪心问题的话，贪心策略是很好想出来的。但是如果之前没接触过这样的问题，就把这个贪心策略当成一个经验积累下来，以后再遇到这样的问题直接朝这方面想就可以了~~）

（想出贪心策略之后，自己构造几组测试用例，如果没有明显的错误的话，直接写代码就 OK 了）（由于这里是赛后题解，我接下来会给出详细证明）。

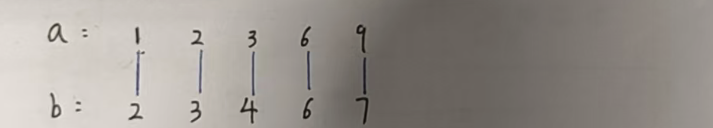
贪心策略的正确性证明：反证法（有兴趣的可以看一看下面）

我们假设不是按照下标一位一位对应，只需要证明这样反着来绝对没有正着来更优就可以了。

假设 i < j，a[i] <= a[j]，b[i] <= b[j]：

如果正着来的话，我们会让 a[i] 和 b[i] 对应，a[j] 和 b[j] 对应。

如果反着来的话，我们会让 a[i] 和 b[j] 对应，a[j] 和 b[i] 对应。

接下来只需要证明在所有的情况下反着来都没有正着来更优就可以了。

我们根据 a[i] a[j] b[i] b[j] 的位置（大小关系）分情况讨论：

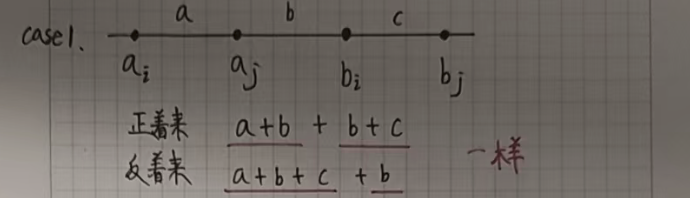
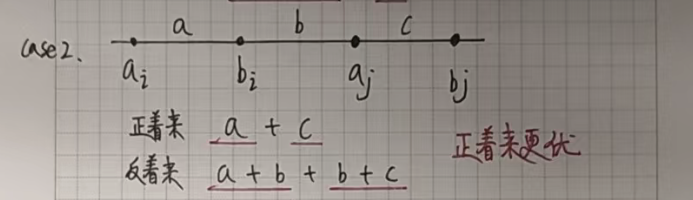
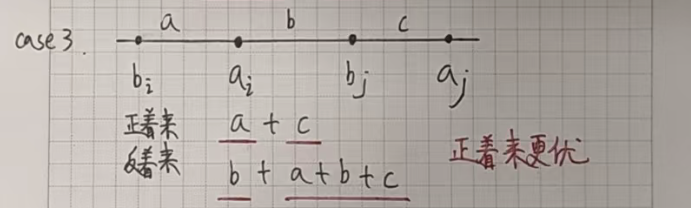
其余情况都类似，就不一一列举了！！！

【代码实现】

#include <iostream>
#include <algorithm>
#include <cmath>using namespace std;typedef long long LL;
const int N = 5e4 + 10;int n;
LL a[N], b[N];int main()
{cin >> n;for(int i = 1; i <= n; i++) cin >> a[i];for(int i = 1; i <= n; i++) cin >> b[i];sort(a + 1, a + 1 + n);sort(b + 1, b + 1 + n);LL ret = 0;for(int i = 1; i <= n; i++)	ret += abs(a[i] - b[i]);cout << ret << endl;return 0;
}

题目五：冷热数据队列

题目链接：冷热数据队列

【题目描述】

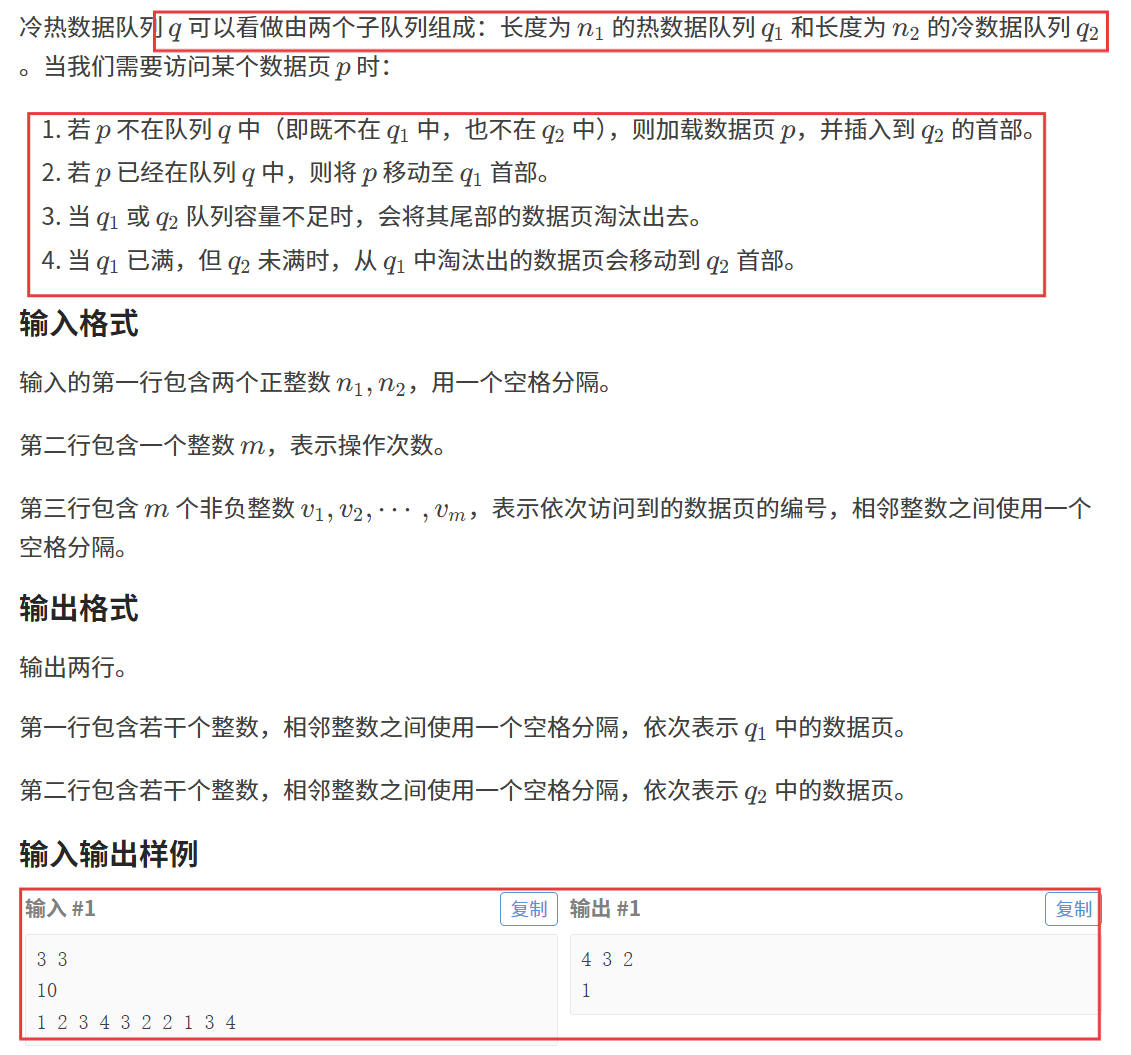
【算法原理】

数据结构 + 模拟

1. 查找 ：哈希表、红黑树；

2. 头插：链表，双端队列；

3. 任意位置删除：双向链表；

4. 尾删：链表，双端队列；

由于本题我们需要执行查找操作，因此我们需要哈希表（或红黑树）这一数据结构。

我们还需要执行任意位置删除和头插操作，因此我们需要双向链表。（STL 中的 List 就行）

执行查找操作要用到的哈希表要能够配合双向链表的删除操作，因此我们这样创建哈希表：

至于 STL 中的 list，我们之前很少使用，这里给大家一些常见的接口：

接下来就是根据题目要求进行模拟的过程了，废话不多说，直接来看代码。 

【代码实现】

#include <iostream>
#include <list>
#include <unordered_map>using namespace std;int n1, n2, m;
list<int> q1, q2;
unordered_map<int, list<int>::iterator> mp1, mp2;int main()
{cin >> n1 >> n2 >> m;while(m--){int x; cin >> x;if(mp1.count(x)){// ɾq1.erase(mp1[x]);mp1.erase(x);// ƶ q1.push_front(x);mp1[x] = q1.begin();}else if(mp2.count(x)){// ɾq2.erase(mp2[x]);mp2.erase(x);// ƶ q1.push_front(x);mp1[x] = q1.begin();}else{q2.push_front(x);mp2[x] = q2.begin();}if(q1.size() > n1){int x = *q1.rbegin();q1.pop_back();mp1.erase(x);q2.push_front(x);mp2[x] = q2.begin();}if(q2.size() > n2){int x = *q2.rbegin();q2.pop_back();mp2.erase(x);}}for(auto x : q1) cout << x << " ";cout << endl;for(auto x : q2) cout << x << " ";cout << endl; return 0;
} 

题目六：倒水

题目链接：倒水

【题目描述】

【算法原理】

二分答案

这道题目有明显的二分题眼，要求的是最小值最大是多少。

分析二段性：

我们假设最终答案 ret 表示最小值的最大情况，我们发现如果再大于 ret 的话，是没有办法做到的，如果小于 ret 的话，我们是可以做到的。因此本题具有明显的二段性，我们就可以尝试使用二分答案来进行解决。

接下来思考如何实现 check 函数？

我们传入一个值 mid，check 函数的功能是判断能否通过倒水使得所有瓶子中的最小值大于等于 x，如果能，说明 mid 落在了左区间。如果不能说明 mid 落到了右区间。

我们只需要从前往后遍历一遍数组，只要该位置的水量大于等于 x，我们就把多余的水往后倒，如果遍历到某一位置发现水量小于 x，就返回 false，如果全部大于等于 x，就返回 true；

我们直接来看代码：

【代码实现】

#include <iostream>
#include <cstring>using namespace std;typedef long long LL;
const int N = 1e5 + 10;LL n, k; 
LL a[N];
LL b[N];bool check(LL x)
{memcpy(b, a, sizeof a);for(int i = 1; i <= n; i++){if(b[i] < x) return false;b[i] -= x;if(i + k <= n) b[i + k] += b[i];} return true;
}int main()
{cin >> n >> k;for(int i = 1; i <= n; i++) cin >> a[i];int l = 0, r = 1e5;while(l < r){int mid = (l + r + 1) >> 1;if(check(mid)) l = mid;else r = mid - 1;}cout << l << endl;return 0;
}

题目七：拼好数

题目链接：拼好数

【题目描述】

【算法原理】

贪心 + 分类讨论

这道题首先大家都可以想到是要统计每一个数中 6 的个数，然后再考虑拼接的问题。

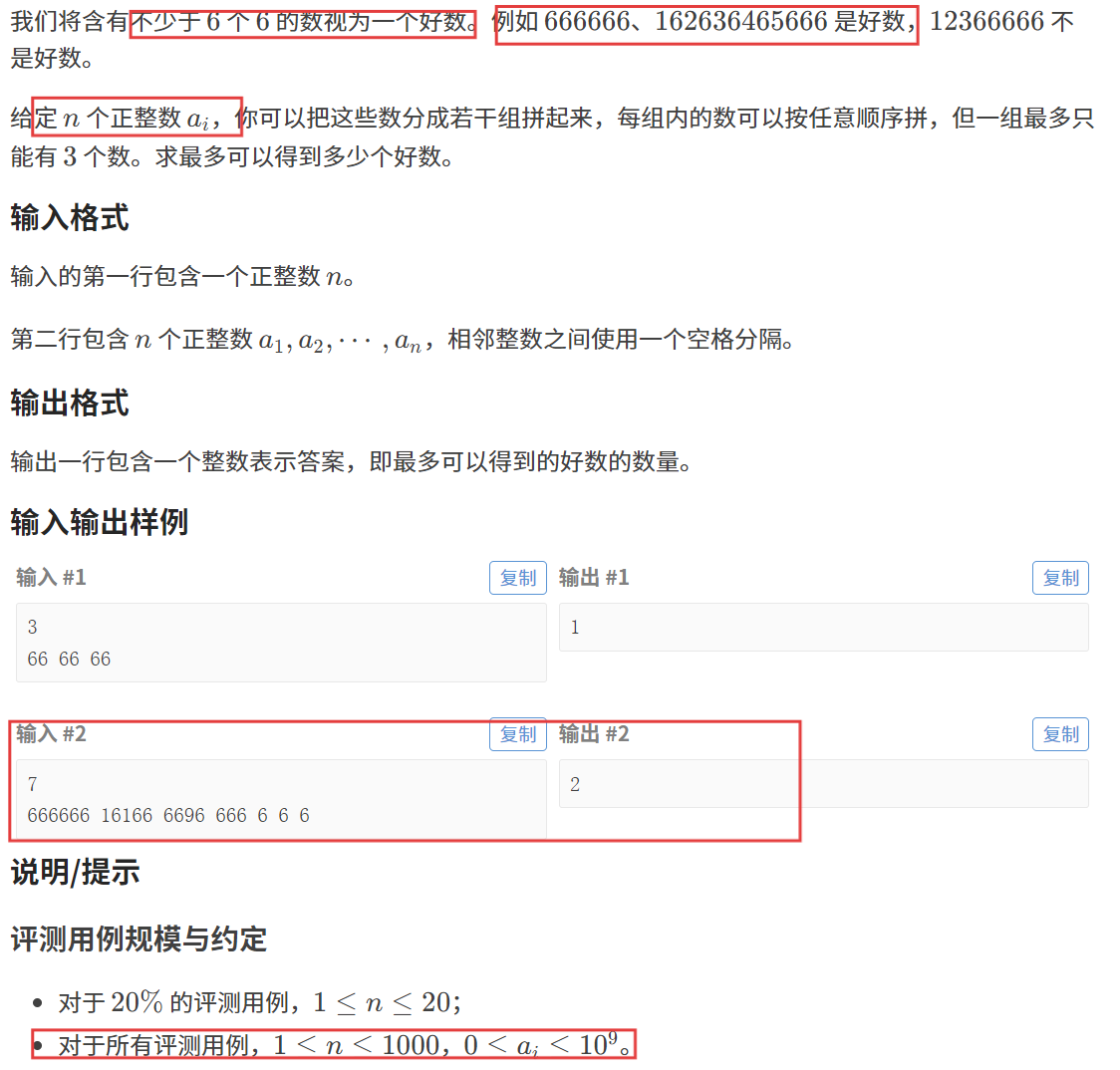
我们预处理出一个 cnt 数组，其中 cnt[i] 表示：出现 6 的次数为 i 时，一共有多少个数。

比如，以第二个测试用例为例，cnt[6] = 1，cnt[3] = 3，cnt[1] = 3；

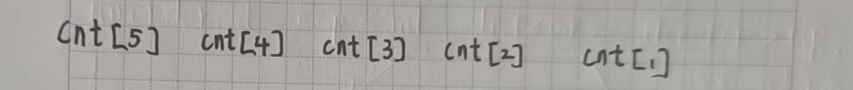
贪心策略：

1. 如果一个数 6 的出现次数大于等于 6，直接让 ret + 1 即可，这个数可以单独成为一个小组。

2. 如果能用 1 去凑，就尽量先使用 1 去凑；因为1 不能单独凑成 6，只能和别的数配合使用。

    能用 1 就先用 1，这样就可以把其余更有用的数保留下来，去凑更多的可能性。

3. 在第二点的基础上，如果能用更少的数凑成，就不用更多的数。

4. 在前面几点的基础上，优先用更容易凑出 6 的数去拼凑。 

直观感受一下，这个贪心策略肯定是正确的~~~

那我们就确定了各种拼凑方式的优先级：

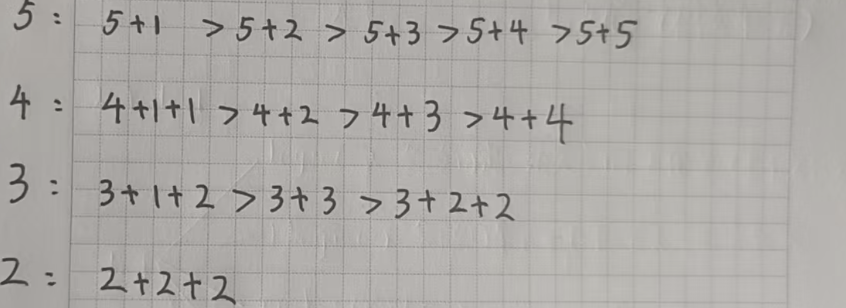
然后我们就可以去写代码了，废话不多说，直接来看代码：

【代码实现】

#include <iostream>using namespace std;const int N = 10;int n;
int cnt[N];// 统计 6 出现的次数 
int calc(int x)
{int c = 0;while(x){if(x % 10 == 6) c++;x /= 10;}return c;
}int main()
{cin >> n;int ret = 0;for(int i = 1; i <= n; i++){int x; cin >> x;int t = calc(x);if(t >= 6) ret++;else cnt[t]++;}// 分类讨论if(cnt[5]){// 5 + 1  5 + 2  5 + 3  5 + 4 for(int i = 1; i <= 4 && cnt[5]; i++){// cnt[i] + cnt[5]if(cnt[5] <= cnt[i]){ret += cnt[5];cnt[i] -= cnt[5];cnt[5] = 0;} else{ret += cnt[i];cnt[5] -= cnt[i];cnt[i] = 0;}} ret += cnt[5] / 2;} if(cnt[4]){// 4 + 1 + 1if(cnt[4] * 2 <= cnt[1]){ret += cnt[4];cnt[1] -= cnt[4] * 2;cnt[4] = 0; } else{ret += cnt[1] / 2;cnt[4] -= cnt[1] / 2;cnt[1] %= 2;}// 4 + 2  4 + 3for(int i = 2; i <= 3 && cnt[4]; i++){// cnt[i] + cnt[4]if(cnt[4] < cnt[i]){ret += cnt[4];cnt[i] -= cnt[4];cnt[4] = 0;} else{ret += cnt[i];cnt[4] -= cnt[i];cnt[i] = 0;}} // 4 + 4ret += cnt[4] / 2;} if(cnt[3]){// 3 + 1 + 2if(cnt[1] && cnt[2]){int t = min(min(cnt[1], cnt[2]), cnt[3]);ret += t;cnt[1] -= t;cnt[2] -= t;cnt[3] -= t;}// 3 + 3ret += cnt[3] / 2;cnt[3] %= 2;// 3 + 2 + 2 -> 2 + 2 + 2 cnt[2] += cnt[3]; }ret += cnt[2] / 3;cout << ret << endl;return 0;
} 

题目八：登山

题目链接：登山

【题目描述】

【算法原理】

本场比赛的压轴题目、逆序对、图论、并查集、单调栈

首先我们要模拟一下输入输出样例，弄明白题目让我们做什么。

这道题目从起点的行走方式如下：

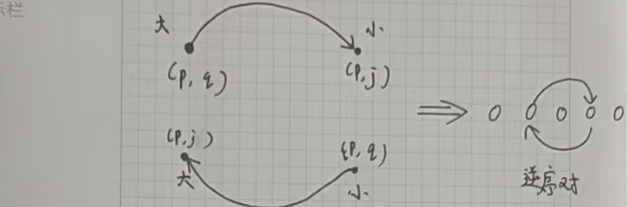
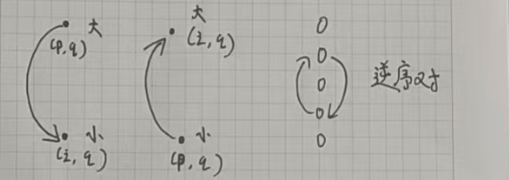
我们先不要考虑二维，可以发现：无论横着看还是竖着看，只要是构成逆序对的话，就有双向边。

那么这道题目就可以转化成一个图论问题：

由于二维坐标不好处理，我们先把二维坐标转化成一维坐标：

根据逆序对建图之后，我们只需要统计每一个连通块（并查集）的最大值，再把所有的点遍历一遍，判断它是在哪一个连通块，直接累加上这个最大值就可以了。

接下来考虑下一个问题：如何把这个图给建出来呢？？？

肯定不能直接把所有的逆序对都连上双向边，因为时间和空间都不允许。（共 nmm + mnn 条边）

但是我们发现，图是没有必要完全建出来的，我们仅需搞定并查集能够找到连通块中的最大值就可以了。

因此，我们这样来处理这个问题：（当成经验积累下来）

我们从前往后遍历数组，如果该元素比前一个位置小，就一直往前合并并查集，顺便删除合并过的元素，直到该元素比前面的元素大。再把该元素存储起来。

类似单调栈的过程，我们用栈来模拟这个过程。

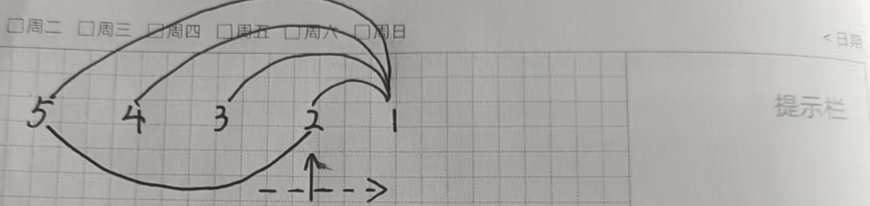
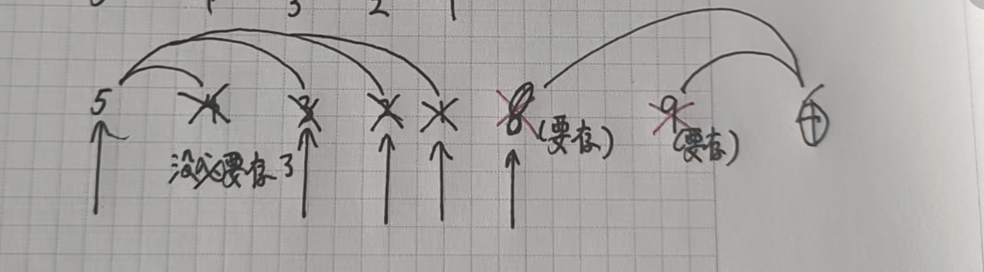
我们直接来看代码：

【代码实现】

#include <iostream>using namespace std;const int N = 1e6 + 10;int n, m;
int a[N];
int fa[N]; // 并查集
int st[N], top; // 栈// 二维转一维
int get_id(int i, int j)
{return i * m + j;
} int find(int x)
{return fa[x] == x ? x : fa[x] = find(fa[x]);
}void merge(int x, int y)
{x = find(x), y = find(y);if(x == y) return;// 小的合并到大的 if(a[x] >= a[y]) fa[y] = x;else fa[x] = y;
}int main() 
{cin >> n >> m;for(int i = 1; i < n * m; i++) fa[i] = i;for(int i = 0; i < n; i++)for(int j = 0; j < m; j++)cin >> a[get_id(i, j)];// 建图for(int i = 0; i < n; i++){top = 0;for(int j = 0; j < m; j++){int t = top, id = get_id(i, j);while(top && a[st[top]] > a[id]){merge(st[top], id);top--;}if(t == top) st[++top] = id;else st[++top] = st[t];}} for(int j = 0; j < m; j++){top = 0;for(int i = 0; i < n; i++){int t = top, id = get_id(i, j);while(top && a[st[top]] > a[id]){merge(st[top], id);top--;}if(t == top) st[++top] = id;else st[++top] = st[t];}} double ret = 0;for(int i = 0; i < n * m; i++) ret += a[find(i)];printf("%.6lf\n", ret / (n * m));return 0;
}

好了，本期的内容就到这里了。期待我们下次见面。