两种最小生成树算法讲解

prim算法精讲

卡码网53. 寻宝

本题题目内容为最短连接，是最小生成树的模板题，那么我们来讲一讲最小生成树。最小生成树可以使用prim算法也可以使用kruskal算法计算出来。本篇我们先讲解prim算法。

最小生成树是所有节点的最小连通子图，即：以最小的成本（边的权值）将图中所有节点链接到一起。图中有n个节点，那么一定可以用n-1条边将所有节点连接到一起。

prim算法是从节点的角度采用贪心的策略每次寻找距离最小生成树最近的节点并加入到最小生成树中。

prim算法核心就是三步，我称为prim三部曲，大家一定要熟悉这三步，代码相对会好些很多：

第一步，选距离生成树最近节点
第二步，最近节点加入生成树
第三步，更新非生成树节点到生成树的距离（即更新minDist数组）

同时，因为使用一维数组，数组的下标和数组如何赋值很重要，不要搞反，导致结果被覆盖。

一定要理解minDist数组，简单说就是一棵树不断记录离自己最近的节点，并吸收进来，再不断循环这个过程

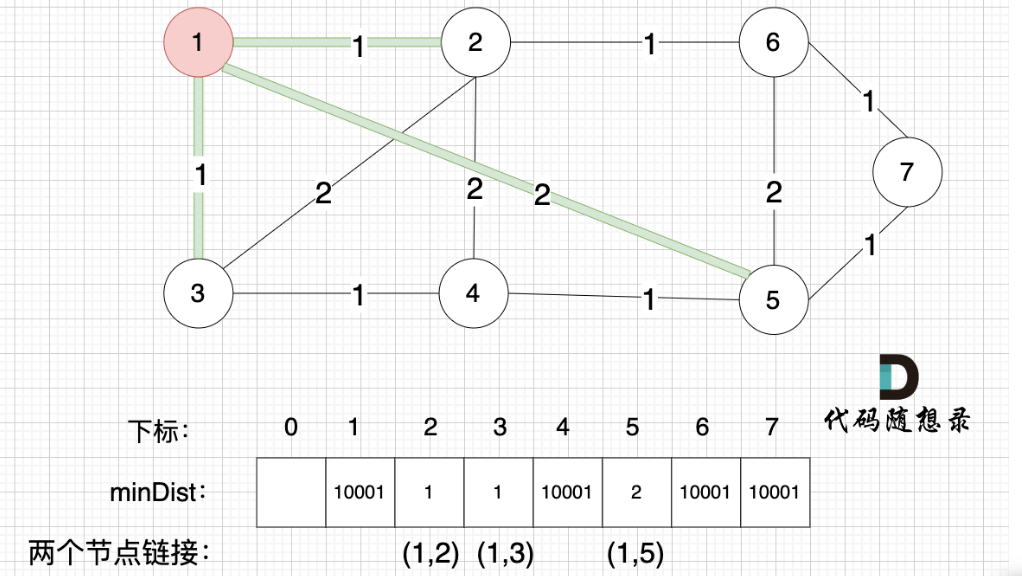
不断吸收新节点，不断以树外节点离树最近的距离做更新，并更新树，循环，最后达到下图效果，具体过程为绿色部分不断延伸（即minDist数组不断更新），最终计算数组和即可

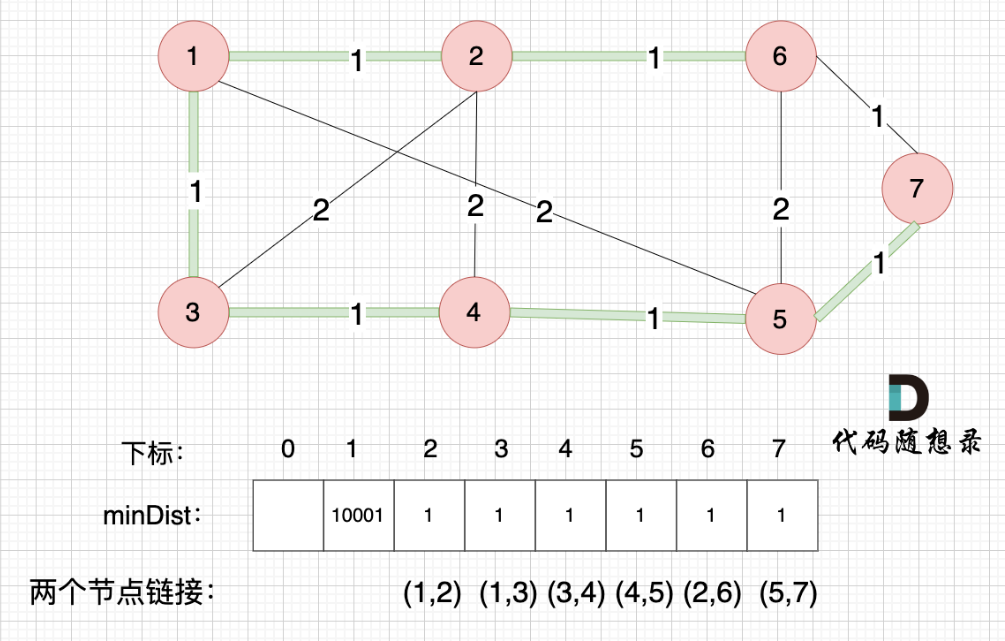
代码实现

记录边，注意初始化数组大小

def prim(v, e, edges):"""Prim算法实现，用于求解无向连通图的最小生成树(MST)总权重参数:v: 顶点数量e: 边的数量edges: 边的列表，每个元素为元组(x, y, k)，表示顶点x与y之间的边权重为k返回:最小生成树的总权重"""import sysimport heapq  # 虽然导入了heapq但未使用，可能是预留或之前版本的残留# 初始化邻接矩阵，大小为(v+1)x(v+1)（顶点编号从1开始）# 初始值设为10001表示无穷大（假设所有边的权重都小于此值）grid = [[10001] * (v + 1) for _ in range(v + 1)]# 读取边的信息并填充邻接矩阵# 由于是无向图，x到y和y到x的权重相同for edge in edges:x, y, k = edge  # x和y为两个顶点，k为边的权重grid[x][y] = kgrid[y][x] = k# minDist数组：记录每个非树节点到生成树的最短距离# 索引0未使用（顶点编号从1开始）minDist = [10001] * (v + 1)# 从顶点1开始构建生成树，因此将其到生成树的距离设为0minDist[1] = 0# isInTree数组：标记顶点是否已加入生成树# True表示已加入，False表示未加入isInTree = [False] * (v + 1)# Prim算法主循环：需要加入v-1条边（构建包含所有v个顶点的树）for i in range(1, v):# 1. 找到当前未加入生成树且距离最近的顶点cur = -1  # 存储当前选中的顶点minVal = sys.maxsize  # 存储当前最小距离（初始为系统最大整数）# 遍历所有顶点，寻找符合条件的顶点for j in range(1, v + 1):# 条件：未加入生成树 且 距离生成树更近if not isInTree[j] and minDist[j] < minVal:minVal = minDist[j]  # 更新最小距离cur = j  # 更新选中的顶点# 2. 将找到的最近顶点加入生成树isInTree[cur] = True# 3. 更新所有未加入生成树的顶点到生成树的最短距离# 以刚加入的cur顶点为中间点，检查是否有更短路径for j in range(1, v + 1):# 条件：未加入生成树 且 通过cur顶点能获得更短距离if not isInTree[j] and grid[cur][j] < minDist[j]:minDist[j] = grid[cur][j]  # 更新最短距离# parent[j] = cur; // 记录最小生成树的边 （注意数组指向的顺序很重要）# 计算最小生成树的总权重：累加顶点2到v的最小距离（顶点1为起点，距离0）result = sum(minDist[2:v+1])return resultif __name__ == "__main__":"""程序入口：读取输入数据并调用prim函数计算结果"""import sys# 读取所有输入数据（一次性读取提高效率，适用于大数据量）input = sys.stdin.readdata = input().split()  # 将输入按空白字符分割为列表# 解析顶点数和边数（前两个元素）v = int(data[0])e = int(data[1])# 解析所有边的信息edges = []index = 2  # 从第三个元素开始是边的信息for _ in range(e):x = int(data[index])y = int(data[index + 1])k = int(data[index + 2])edges.append((x, y, k))  # 将边信息存入列表index += 3  # 移动到下一条边的起始位置# 调用prim算法计算结果并输出result = prim(v, e, edges)print(result)

kruskal算法精讲

通过贪心的思路，从边出发，（在是否同一集合的情况下判断）不断吸收最小权值的边。再次注意本题是要求连接所有节点！！

但在代码中，如果将两个节点加入同一个集合，又如何判断两个节点是否在同一个集合呢？我们在并查集开篇的时候就讲了，并查集主要就两个功能：

将两个元素添加到一个集合中
判断两个元素在不在同一个集合

代码实现

本题图示是绿色线条的不断延伸（每次多一条边），上题为以节点为中心不断更新最短距离数组

lambda 是 Python 中的匿名函数，语法为 lambda 参数: 表达式，通常用于简化代码，lambda 中的 edge 是一个形参，sort 方法在遍历 edges 时会自动将列表中的每个元素作为实参传给它，因此 edge 能依次指向 edges 中的所有元素

# 定义边(Edge)类，用于存储一条边的信息
class Edge:def __init__(self, l, r, val):self.l = l      # 边的左顶点self.r = r      # 边的右顶点self.val = val  # 边的权重值# 初始化常量和并查集数组
n = 10001               # 最大顶点数限制
father = list(range(n)) # 并查集数组，father[u]表示u的父节点def init():"""初始化并查集，让每个节点的父节点都是自己"""global fatherfather = list(range(n))def find(u):"""查找节点u的根节点，同时进行路径压缩路径压缩是为了加快后续的查询速度"""if u != father[u]:# 递归查找根节点，并将当前节点的父节点直接指向根节点father[u] = find(father[u])return father[u]def join(u, v):"""合并两个集合：将节点v所在的集合合并到节点u所在的集合前提是u和v已经是各自集合的根节点"""u = find(u)v = find(v)if u != v:# 将v的父节点设置为u，实现两个集合的合并father[v] = udef kruskal(v, edges):"""Kruskal算法实现：求解最小生成树的总权重参数：v: 顶点数量edges: 边的列表，每个元素是Edge对象返回：最小生成树的总权重"""# 1. 按边的权重从小到大排序（核心步骤）edges.sort(key=lambda edge: edge.val)# 2. 初始化并查集init()# 3. 存储最小生成树的总权重result_val = 0# 4. 遍历所有排序后的边，尝试加入生成树for edge in edges:# 查找两个顶点所在集合的根节点x = find(edge.l)y = find(edge.r)# 如果根节点不同，说明不在同一个集合，不会形成环if x != y:# 将这条边加入最小生成树result_val += edge.val# 合并两个集合join(x, y)return result_valif __name__ == "__main__":"""程序入口：读取输入并调用Kruskal算法计算结果"""import sys# 一次性读取所有输入数据input = sys.stdin.readdata = input().split()  # 按空白字符分割成列表# 解析顶点数和边数v = int(data[0])e = int(data[1])# 解析所有边的信息edges = []index = 2  # 从第三个元素开始是边的信息for _ in range(e):v1 = int(data[index])v2 = int(data[index + 1])val = int(data[index + 2])edges.append(Edge(v1, v2, val))  # 创建Edge对象并添加到列表index += 3  # 移动到下一条边的起始位置# 调用Kruskal算法计算结果并输出result_val = kruskal(v, edges)print(result_val)