LeetCode111.二叉树的最小深度：

题目描述：

给定一个二叉树，找出其最小深度。

最小深度是从根节点到最近叶子节点的最短路径上的节点数量。

说明：叶子节点是指没有子节点的节点。

示例 1：

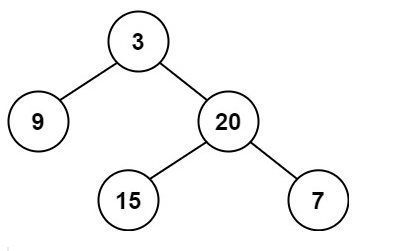
输入：root = [3,9,20,null,null,15,7]
输出：2
示例 2：

输入：root = [2,null,3,null,4,null,5,null,6]
输出：5

提示：

树中节点数的范围在 [0, 10^5] 内
-1000 <= Node.val <= 1000

思路：

涉及树的左右节点问题，我们可以借鉴闫氏DP的思想，也就是每次只是看当前根节点跟左右子节点（左右子节点下可能存在子树），我们需要看怎么去维护当前左右子节点的信息
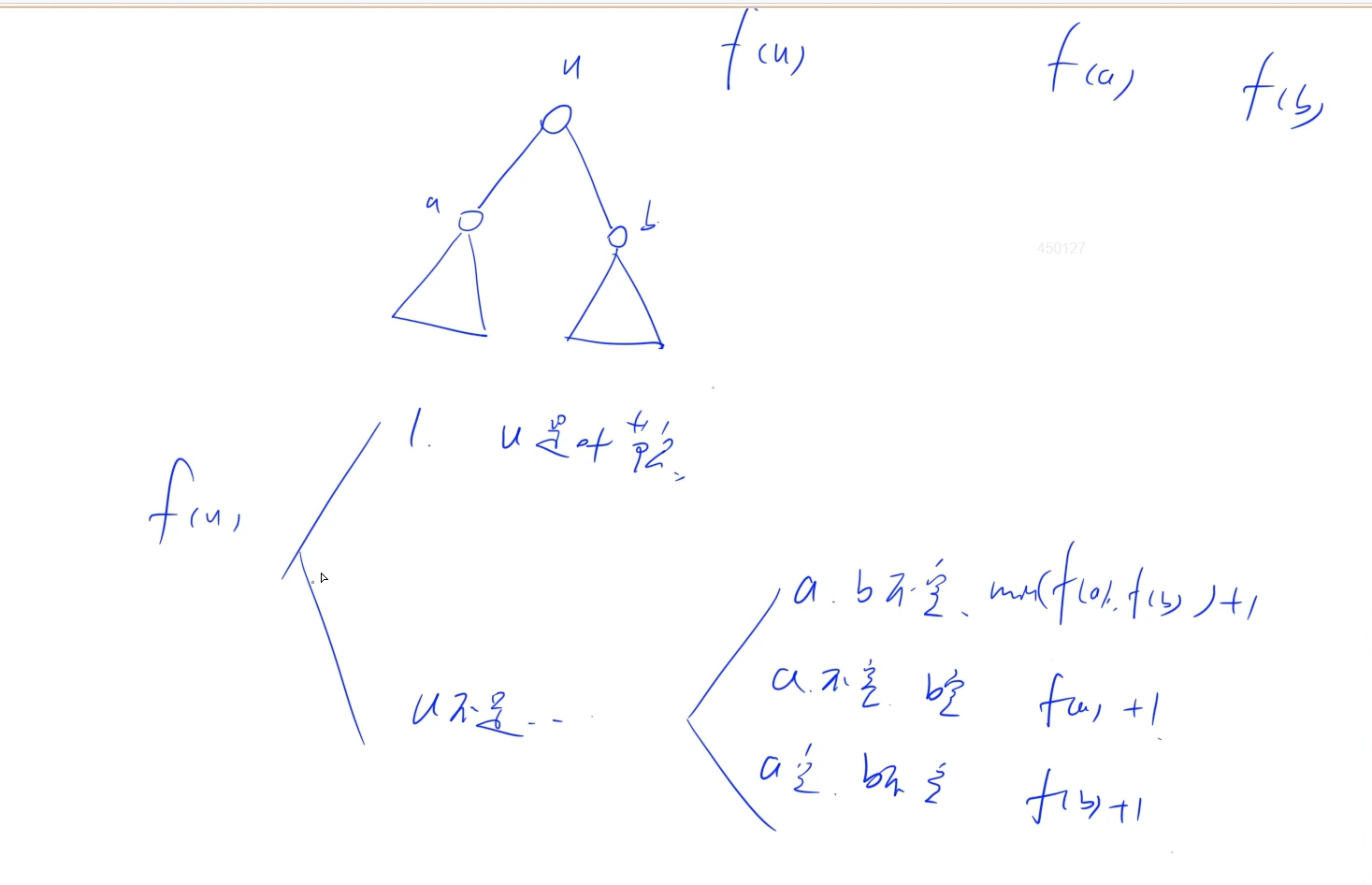
比如这题： 我们需要求的是最小的深度，那么我们就当前根节点以及它的左右子节点来看，根节点的最小深度看成f(n), 左右子节点分别看成f(a), f(b)，那么我们可以分情况讨论f(n)跟f(a), f(b)之间的关系：
1.a和b都存在： 那么f(n) = min(f(a), f(b)) + 1
2.a存在b不存在： f(n) = min(f(a)) + 1
3.a不存在b存在： f(n) = min(f(b)) + 1
4.a和b都不存在： 那么f(n) = 1
于是我们可以发现当前跟节点的最小深度只跟左右子节点的情况有关，所以我们可以递归处理每个子树的关系，最终将结果聚合到根节点下

时间复杂度：

每个节点会查询一次，所以总的时间复杂度是O(n)的

注释代码：

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:int minDepth(TreeNode* root) {if(!root) return 0; //当前节点不存在，返回0if(!root -> right && !root -> left) return 1; //没有左右节点，说明当前是叶子节点if(root -> right && root -> left) return min(minDepth(root -> left), minDepth(root -> right)) + 1; //两者都存在则返回深度最小的if(root -> left) return minDepth(root -> left) + 1; //存左子节点那么返回左子树中最小的深度+ 1（当前节点）return minDepth(root -> right) + 1; //否则就是存在右子节点，那么返回右子树中最小的深度+ 1，以此递归}
};

纯享版：

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:int minDepth(TreeNode* root) {if(!root) return 0;if(!root -> left && !root -> right) return 1;if(root -> left && root -> right) return min(minDepth(root -> left), minDepth(root -> right)) + 1;if(root -> left) return minDepth(root -> left) + 1;return minDepth(root -> right) + 1;}
};

---

LeetCode112.路径总和：

题目描述：

给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径，这条路径上所有节点值相加等于目标和 targetSum 。如果存在，返回 true ；否则，返回 false 。

叶子节点 是指没有子节点的节点。

示例 1：

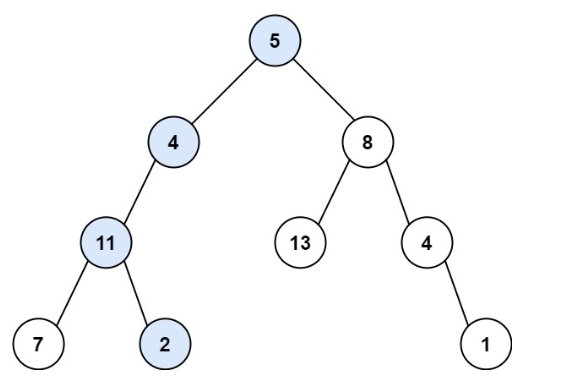
输入：root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22
输出：true
解释：等于目标和的根节点到叶节点路径如上图所示。

示例 2：

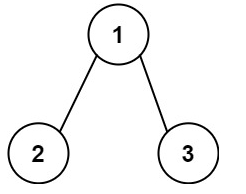
输入：root = [1,2,3], targetSum = 5
输出：false
解释：树中存在两条根节点到叶子节点的路径：
(1 --> 2): 和为 3
(1 --> 3): 和为 4
不存在 sum = 5 的根节点到叶子节点的路径。

示例 3：

输入：root = [], targetSum = 0
输出：false
解释：由于树是空的，所以不存在根节点到叶子节点的路径。

提示：

树中节点的数目在范围 [0, 5000] 内
-1000 <= Node.val <= 1000
-1000 <= targetSum <= 1000

思路：

这类需要根据父子节点的值来得出答案的题型一般有两种思路： 一种自下向上： 就是利用儿子节点来得出父亲节点的目标值； 一种是自上向下： 使用父亲节点的值来得出儿子节点上的目标值；
这题就是利用自上向下的思路： 设定父节点u, 左右儿子节点分别为a, b ： 那么f(a) 和 f(b) 的路径值就是在父亲节点的基础上加上自己本身的节点值也就是 f(a) = f(u) + a -> val f(b) = f(u) + b -> val 以此类推，直到延展至叶子节点，而这里为了节省变量空间，将原本需要使用sum进行总和累加的变量省去，每次让targetSum减去当前节点的节点值，然后将减后的targetSum值继续作为参数传下去，以此递归，直到延展至叶子节点时判断最后的targetSum是否恰好为0，为0 则说明这条路径刚好满足条件，否则说明这条路径节点值总和不是targetSum

时间复杂度：

每个节点仅被遍历一次，且递归过程中维护 targetSum的时间复杂度是 O(1)，所以总时间复杂度是 O(n)

注释代码：

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:bool hasPathSum(TreeNode* root, int targetSum) {if(!root) return false; //如果当前节点不存在返回falsetargetSum -= root -> val;  //让target Sum减去当前节点的值if(!root -> left && !root -> right) return !targetSum;  //如果是叶子节点那就判断当前target Sum的值是否刚好减为0//然后如果当前节点有左儿子或者右儿子，那么在当前节点和targetSum的基础上递归下去return root -> left && hasPathSum(root -> left,  targetSum) || root -> right && hasPathSum(root -> right, targetSum);}
};

纯享版：

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:bool hasPathSum(TreeNode* root, int targetSum) {if(!root) return false;targetSum -= root -> val;if(!root -> left && !root -> right && targetSum == 0) return true;return root -> left && hasPathSum(root -> left, targetSum) || root -> right && hasPathSum(root -> right, targetSum);}
};

---

LeetCode113.路径总和Ⅱ：

题目描述：

给你二叉树的根节点 root 和一个整数目标和 targetSum ，找出所有 从根节点到叶子节点 路径总和等于给定目标和的路径。

叶子节点 是指没有子节点的节点。

示例 1：

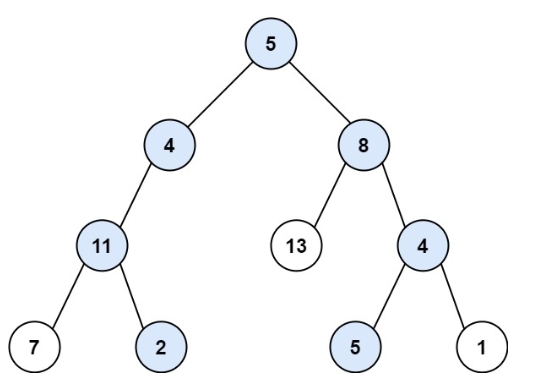
输入：root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
输出：[[5,4,11,2],[5,8,4,5]]

示例 2：

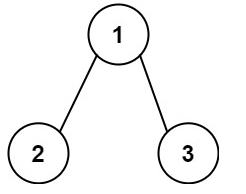
输入：root = [1,2,3], targetSum = 5
输出：[]

示例 3：

输入：root = [1,2], targetSum = 0
输出：[]

提示：

树中节点总数在范围 [0, 5000] 内
-1000 <= Node.val <= 1000
-1000 <= targetSum <= 1000

思路：

跟 LeetCode12.路径总和 思路一致，但是Ⅰ只要找到合法路径就return了，Ⅱ则需要将所有的合法路径存下来， 那么只需要开一个容器并且记录使得targetSum为0的路径即可，形式便是dfs形式

时间复杂度：

每个节点会搜一次，并且每个节点上的操作时间是O(1)的，总的时间复杂度就是O(n)的

注释代码：

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:vector<vector<int>> res;vector<int> path;vector<vector<int>> pathSum(TreeNode* root, int targetSum) {if(root) dfs(root, targetSum);return res;}void dfs(TreeNode* root, int targetSum){path.push_back(root -> val); //将当前节点存入当前路径targetSum -= root -> val;if(!root -> left && !root -> right) //如果当前节点是叶子节点{if(targetSum == 0)  //并且targetSum为0，说明该路径是合法的{res.push_back(path); //加到答案集合中}}else{if(root -> left) dfs(root -> left, targetSum);  //如果不是叶子节点，并且左儿子存在的话递归左儿子if(root -> right) dfs(root -> right, targetSum); //不是叶子节点并且右儿子存在的话递归右儿子}path.pop_back(); //恢复现场}
};

纯享版：

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:vector<vector<int>> res;vector<int> path;vector<vector<int>> pathSum(TreeNode* root, int targetSum) {if(root) dfs(root, targetSum);return res;}void dfs(TreeNode* root, int targetSum){path.push_back(root -> val);targetSum -= root -> val;if(!root -> left && !root -> right){if(targetSum == 0) res.push_back(path);}else{if(root -> left) dfs(root -> left, targetSum);if(root -> right) dfs(root -> right, targetSum);}path.pop_back();}
};

---

LeetCode114.二叉树展开为链表：

题目描述：

给你二叉树的根结点 root ，请你将它展开为一个单链表：

展开后的单链表应该同样使用 TreeNode ，其中 right 子指针指向链表中下一个结点，而左子指针始终为 null 。
展开后的单链表应该与二叉树 先序遍历 顺序相同。

示例 1：

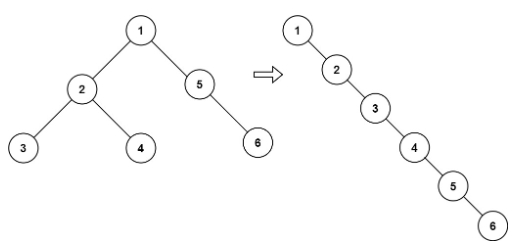
输入：root = [1,2,5,3,4,null,6]
输出：[1,null,2,null,3,null,4,null,5,null,6]

示例 2：

输入：root = []
输出：[]

示例 3：

输入：root = [0]
输出：[0]

提示：

树中结点数在范围 [0, 2000] 内
-100 <= Node.val <= 100

进阶：你可以使用原地算法（O(1) 额外空间）展开这棵树吗？

思路：

这里是使用二叉树的前序遍历：

稍微变形一下就是如果当前节点存在左儿子，就找到当前节点下左子树的右链，将其插入右子树中，然后跳到右儿子继续循环处理，直到所有节点都不存在左儿子：

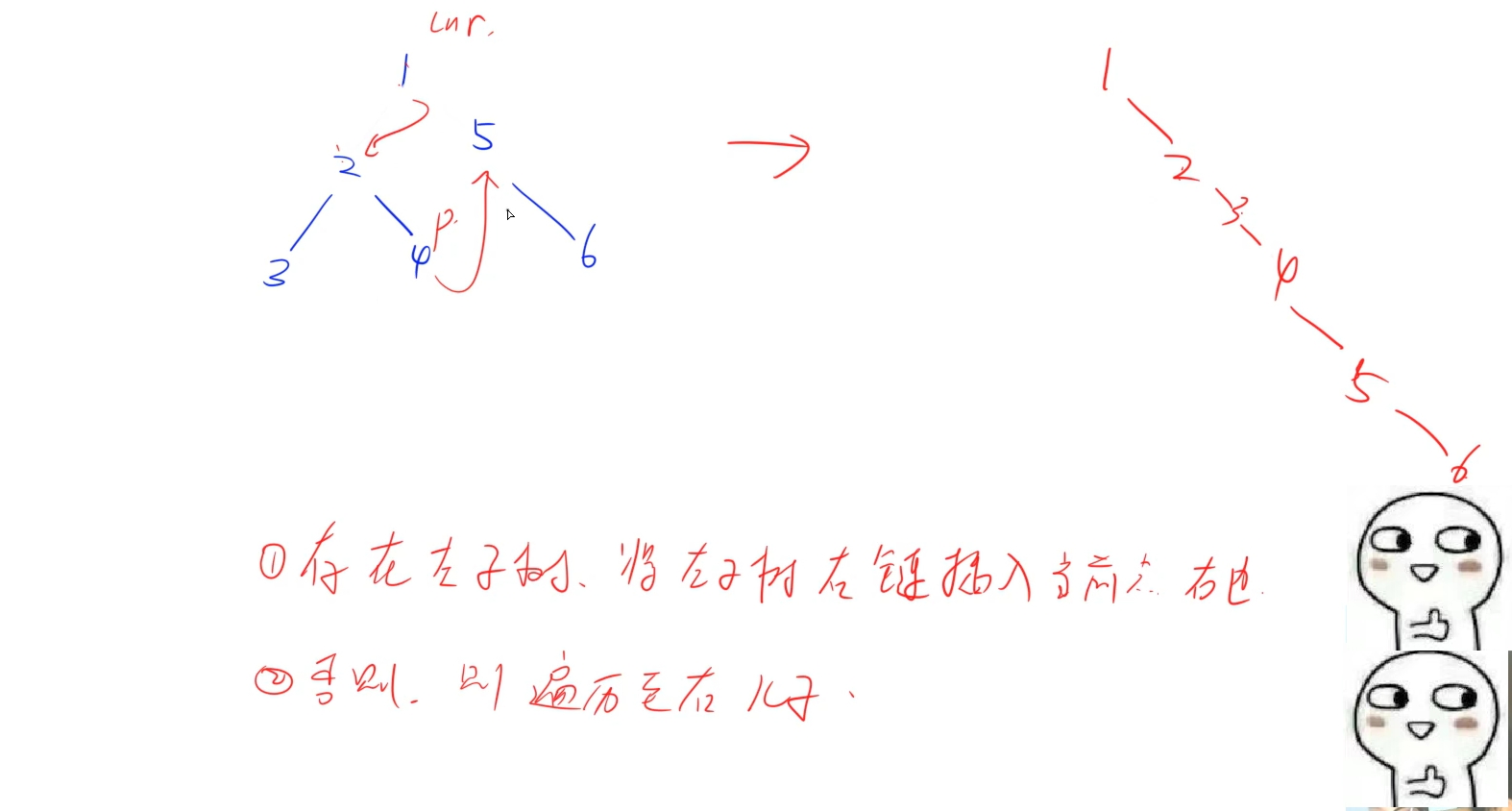
形成链表的做法也跟链表做法相似： 找到当前节点下的左儿子，以及左子树的右链的最后一个节点，让左子树的右链最后一个节点右儿子指向当前节点原先的右儿子，再让当前节点的右儿子指向当前节点的左儿子，具体如上图所示

时间复杂度：

虽然两重while循环，但是外层循环会将每个节点遍历一次，内层循环会将除了根节点之外的其他右链内部节点遍历一次，也就是说每个节点最多遍历两次，所以时间复杂度是O(n)的

注释代码：

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:void flatten(TreeNode* root) {while(root){auto p = root -> left; //找到左儿子if(p) //如果存在左儿子，那么找到左儿子下的右链{while(p -> right) p = p -> right; //找到左子树的右链p -> right = root -> right; //将右链插入右子树中root -> right = root -> left;root -> left = NULL;  //当前节点就没有左子树了}root = root -> right; //将当前节点移动到右节点继续找左子树的右链}}
};

纯享版：

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:void flatten(TreeNode* root) {while(root){auto p = root -> left;if(p){while(p -> right) p = p -> right;p -> right = root -> right;root -> right = root -> left;root -> left = NULL;}root = root -> right;}}
};

---

LeetCode115.不同的子序列：

题目描述：

给你两个字符串 s 和 t ，统计并返回在 s 的 子序列 中 t 出现的个数，结果需要对 109 + 7 取模。

示例 1：

输入：s = “rabbbit”, t = “rabbit”
输出：3
解释：
如下所示, 有 3 种可以从 s 中得到 “rabbit” 的方案。

示例 2：

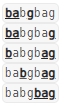
输入：s = “babgbag”, t = “bag”
输出：5
解释：
如下所示, 有 5 种可以从 s 中得到 “bag” 的方案。

提示：

1 <= s.length, t.length <= 1000
s 和 t 由英文字母组成

思路：

诸如此类字符匹配的题型优先考虑用DP：
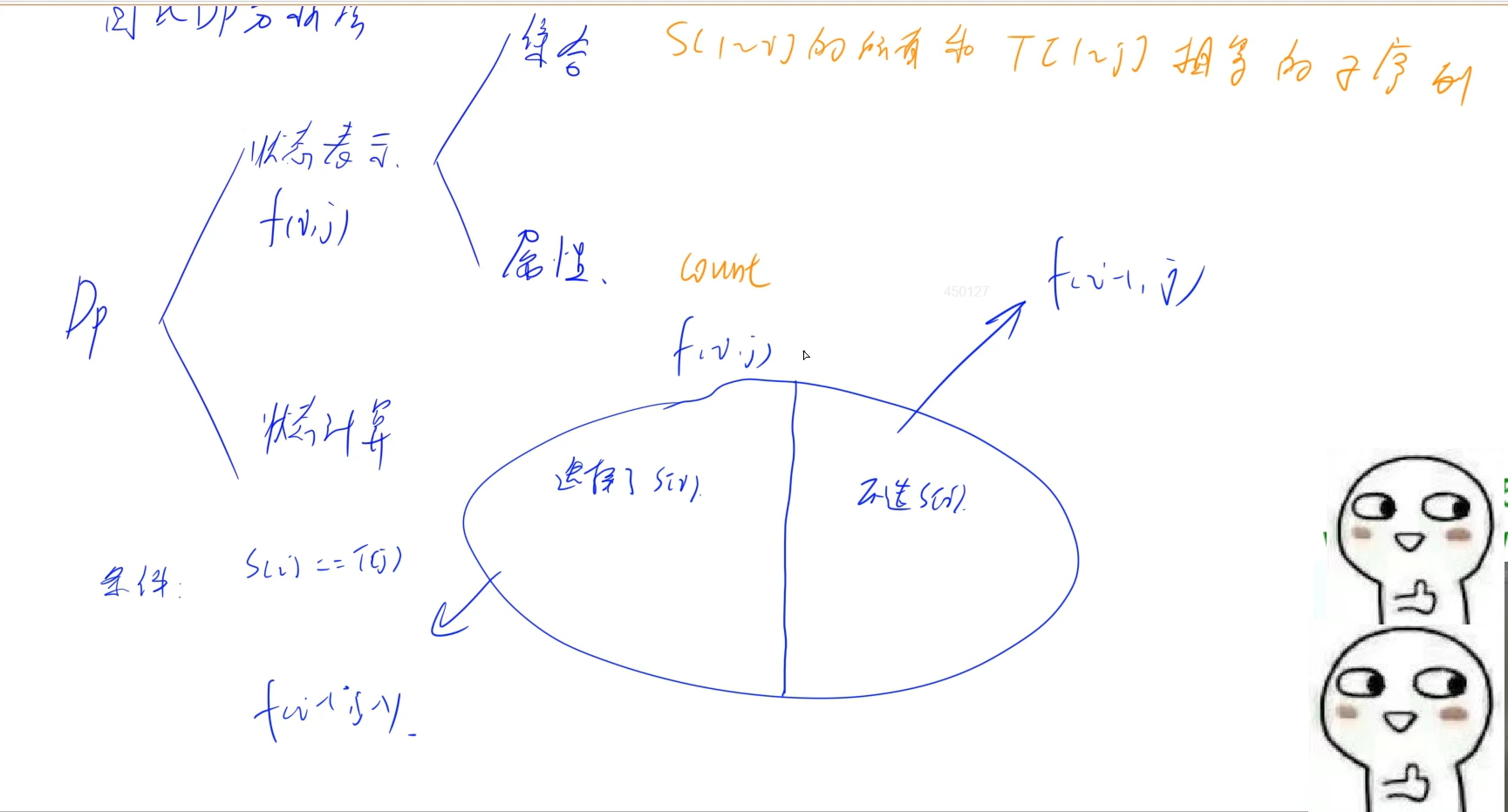
通过闫氏DP法：
1.设定集合f(i, j): 表示由s 的前1 ~i 字符组成的所有跟 t的 1~j字符相同的子序列数量
2.集合划分： 分情况考虑， DP问题一般对末尾的一位的情况进行讨论，这里也是，对于跟t的 1 ~j字符组成的字符串相同的子序列中，是否包含s的第i位进行讨论：
(1)不包含s[i]的子序列： 也就是说在不包含s[i]的情况下，所求的f[i][j]也就是由s的1~i字符中组成的子序列中跟t的1~j字符串相同的数量是不包含s[i]的数量，也就等价于求由s的1~i-1字符中组成的子序列中跟t的1~j字符串相同的数量： f[i][j] = f[i - 1][j]
(2)包含s[i]的子序列: 首先要满足s[i] == t[j]条件，如果选了s[i]那么， 满足条件的所有子序列都是包含s[i]的，于是变成从s的1~i-1字符中选，让其组成的子序列中跟t的1~j-1字符组成的字符串相同： f[i][j] += f[i - 1][j - 1](相加是因为满足条件的子序列可以包含s[i] 也可以不包含s[i])

时间复杂度：O(nm): dp问题一般先分析状态数量

注释代码：

class Solution {
public:const int mod = 1e9 + 7; //设定modint numDistinct(string s, string t) {int n = s.size(), m = t.size();s = ' ' + s, t = ' ' + t; //从1开始比较好处理//设定集合f(i, j)为s的1~i字符组成的所有子序列中等于t的1~j字符串的子序列个数vector<vector<long long>> f(n + 1, vector<long long> (m + 1));for(int i = 0; i <= n; i++) f[i][0] = 1;  //s的前1~i个字符选零个来匹配t的前零个字符是一种方案for(int i = 1; i <= n; i++){for(int j = 1; j <= m; j++){//当不选s的第i个字符，那么s的1 ~i个字符中匹配t的1~j的子序列数量就为s的1~i- 1个字符中匹配t的1~j的子序列数量f[i][j] = f[i - 1][j] % mod; //如果选s的第i个字符， 那么首先判断s[i] 能不能和t[j]匹配上，如果能匹配上//那么s的1 ~i个字符中匹配t的1~j的子序列数量就要在本身的基础上加上s的1~i- 1个字符中匹配t的1~j - 1的子序列数量if(s[i] == t[j]) f[i][j] += f[i - 1][j - 1] % mod;}}return f[n][m];}
};

纯享版：

class Solution {
public:const int mod = 1e9 + 7;int numDistinct(string s, string t) {int n = s.size(), m = t.size();s = ' ' + s, t = ' '  + t;vector<vector<long long>> f(n + 1, vector<long long> (m + 1));for(int i = 0; i <= n; i++) f[i][0] = 1;for(int i = 1; i <= n; i++){for(int j = 1; j <= m; j++){f[i][j] = f[i - 1][j] % mod;if(s[i] == t[j]) f[i][j] += f[i - 1][j - 1] % mod;}}return f[n][m];}
};

---

LeetCode116.填充每个节点的下一个右侧节点指针：

题目描述：

给定一个 完美二叉树 ，其所有叶子节点都在同一层，每个父节点都有两个子节点。二叉树定义如下：

struct Node {
int val;
Node *left;
Node *right;
Node *next;
}
填充它的每个 next 指针，让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点，则将 next 指针设置为 NULL。

初始状态下，所有 next 指针都被设置为 NULL。

示例 1：

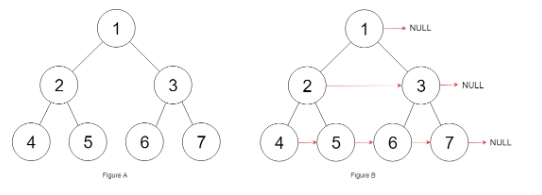
输入：root = [1,2,3,4,5,6,7]
输出：[1,#,2,3,#,4,5,6,7,#]
解释：给定二叉树如图 A 所示，你的函数应该填充它的每个 next 指针，以指向其下一个右侧节点，如图 B 所示。序列化的输出按层序遍历排列，同一层节点由 next 指针连接，‘#’ 标志着每一层的结束。

示例 2:

输入：root = []
输出：[]

提示：

树中节点的数量在 [0, 2^12 - 1] 范围内
-1000 <= node.val <= 1000

进阶：

你只能使用常量级额外空间。
使用递归解题也符合要求，本题中递归程序占用的栈空间不算做额外的空间复杂度

思路：

原本这题是可以直接使用层序遍历的做法直接在每一层进行指向即可，但是进阶做法需要使用常数空间的话就只能利用原树直接进行指向了，那么可以发现每一层的节点指向都需要用到上一层的节点指向才能完整连接每一层的所有节点，而上层又需要更上一层的节点指向，所以我们需要从根节点开始维护，一层一层往下指向：（这里为了通俗易懂些使用样例进行说明）
1.从根节点1开始，先找到根节点1下最左边的节点，也就是当前根节点的左儿子2，让2指向根节点的右儿子3： p -> left -> next = p -> right (p 依次表示上一层的每个节点)
2.进入下一层，同样是找到下一层的最左边的节点，也就是上一层节点2的左儿子4： root = root -> left，同样的让4指向2的右儿子5
3.由于5需要指向6，这里就需要利用上一层的指向关系： 因为上一层的2后面有指向的节点3：p -> next存在， 则，让5指向3的左儿子6：p -> left -> next = p -> next -> left， 然后p往后移指向上一层的后一个节点3：p = p -> next, 最后就是让3的左儿子指向3的右儿子： p -> right -> next = p -> left ,由于上一层节点3的后面没有后续节点了，所以退出当前层的循环，判断下一层的最左边节点是否存在，不存在则无需进入下一层，循环结束

时间复杂度：

每个节点仅会遍历一次，遍历时修改指针的时间复杂度是 O(1)，所以总时间复杂度是 O(n)

注释代码：

/*
// Definition for a Node.
class Node {
public:int val;Node* left;Node* right;Node* next;Node() : val(0), left(NULL), right(NULL), next(NULL) {}Node(int _val) : val(_val), left(NULL), right(NULL), next(NULL) {}Node(int _val, Node* _left, Node* _right, Node* _next): val(_val), left(_left), right(_right), next(_next) {}
};
*/class Solution {
public:Node* connect(Node* root) {if(!root) return root;auto cur = root; //存储root节点，作为返回while(root -> left){for(auto p = root; p ; p = p -> next)  //遍历当前层的每个节点{p -> left -> next = p -> right;  //让当前节点下的左儿子指向当前节点下的右儿子if(p -> next) p -> right -> next = p -> next -> left; //如果当前节点存在后续节点，则让当前节点下的右儿子指向当前层的下一个节点的左儿子}root = root -> left; //进入下一层的最左边节点}return cur;}
};

纯享版：

/*
// Definition for a Node.
class Node {
public:int val;Node* left;Node* right;Node* next;Node() : val(0), left(NULL), right(NULL), next(NULL) {}Node(int _val) : val(_val), left(NULL), right(NULL), next(NULL) {}Node(int _val, Node* _left, Node* _right, Node* _next): val(_val), left(_left), right(_right), next(_next) {}
};
*/class Solution {
public:Node* connect(Node* root) {if(!root) return root;auto cur = root;while(root -> left){for(auto p = root; p; p = p -> next){p -> left -> next = p -> right;if(p -> next) p -> right -> next = p -> next -> left;}root = root -> left;}return cur;}
};

---

LeetCode117.填充每个节点的下一个右侧节点指针Ⅱ：

题目描述：

给定一个二叉树：

struct Node {
int val;
Node *left;
Node *right;
Node *next;
}
填充它的每个 next 指针，让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点，则将 next 指针设置为 NULL 。

初始状态下，所有 next 指针都被设置为 NULL 。

示例 1：

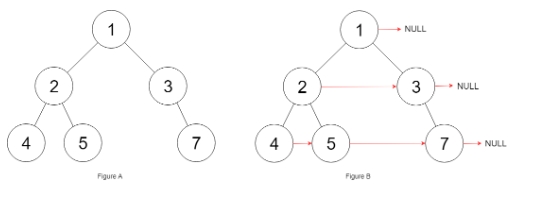
输入：root = [1,2,3,4,5,null,7]
输出：[1,#,2,3,#,4,5,7,#]
解释：给定二叉树如图 A 所示，你的函数应该填充它的每个 next 指针，以指向其下一个右侧节点，如图 B 所示。序列化输出按层序遍历顺序（由 next 指针连接），‘#’ 表示每层的末尾。

示例 2：

输入：root = []
输出：[]

提示：

树中的节点数在范围 [0, 6000] 内
-100 <= Node.val <= 100
进阶：

你只能使用常量级额外空间。
使用递归解题也符合要求，本题中递归程序的隐式栈空间不计入额外空间复杂度。

思路：

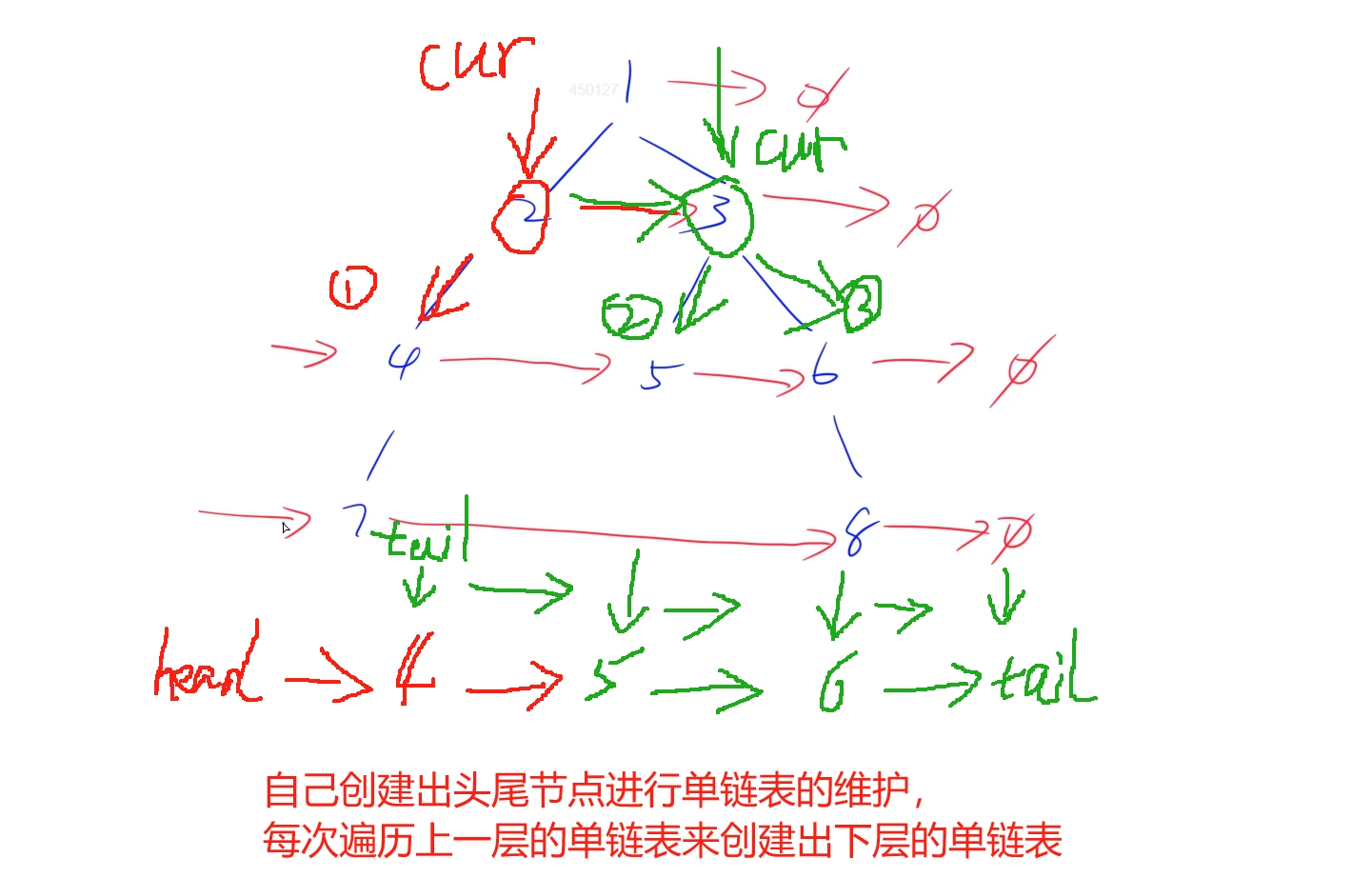
由于这题的进阶做法也同样不能使用额外空间，同时这里还是与上题同样的思想，使用上一层节点来维护下层的指向关系，但是可能不存在部分节点，就不能使用上题所述方法进行链表连接，这里想到只需要创建链表的头尾两个节点，每次只要发现当前节点有左儿子就优先将左儿子添加到尾节点之前，然后看右儿子，也进行同样操作，这样从前往后遍历上一层的节点，就能将下一层的节点全部依次添加到每层创建的头尾节点之间

时间复杂度：

每个节点仅会遍历一次。对于每个节点，遍历时维护下一层链表的时间复杂度是 O(1)，所以总时间复杂度是 O(n)。

注释代码：

/*
// Definition for a Node.
class Node {
public:int val;Node* left;Node* right;Node* next;Node() : val(0), left(NULL), right(NULL), next(NULL) {}Node(int _val) : val(_val), left(NULL), right(NULL), next(NULL) {}Node(int _val, Node* _left, Node* _right, Node* _next): val(_val), left(_left), right(_right), next(_next) {}
};
*/class Solution {
public:Node* connect(Node* root) {if(!root) return root;auto cur = root;while(cur){auto head = new Node(-1); //每一层的头节点auto tail = head; //每一层的尾节点for(auto p = cur; p; p = p -> next) //遍历当前层的每一个节点，利用当前层更新下一层的链表指向{if(p -> left) tail = tail -> next = p -> left; //如果存在左儿子那么将左儿子插入尾节点之前if(p -> right) tail = tail -> next = p -> right; //如果存在右儿子那么将右儿子插入尾节点之前}cur = head -> next;  //转至下一层的头节点下的第一个节点}return root;}
};

纯享版：

/*
// Definition for a Node.
class Node {
public:int val;Node* left;Node* right;Node* next;Node() : val(0), left(NULL), right(NULL), next(NULL) {}Node(int _val) : val(_val), left(NULL), right(NULL), next(NULL) {}Node(int _val, Node* _left, Node* _right, Node* _next): val(_val), left(_left), right(_right), next(_next) {}
};
*/class Solution {
public:Node* connect(Node* root) {if(!root) return root;auto cur = root;while(cur){auto head = new Node(-1);auto tail = head;for(auto p = cur; p; p = p -> next){if(p -> left) tail = tail -> next = p -> left;if(p -> right) tail = tail -> next = p -> right;}cur = head -> next;}return root;}
};

---

LeetCode118.杨辉三角：

题目描述：

给定一个非负整数 numRows，生成「杨辉三角」的前 numRows 行。

在「杨辉三角」中，每个数是它左上方和右上方的数的和。

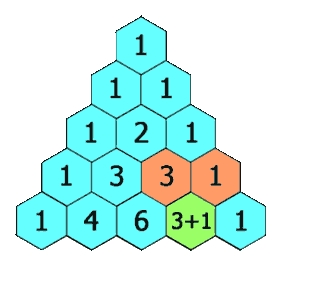
示例 1:

输入: numRows = 5
输出: [[1],[1,1],[1,2,1],[1,3,3,1],[1,4,6,4,1]]

示例 2:

输入: numRows = 1
输出: [[1]]

提示:

1 <= numRows <= 30

思路：

递推即可：这里主要需要注意的是在转换成矩阵来看的话当前格子是由上一行的同一列和上一行前一列的两个格子的和

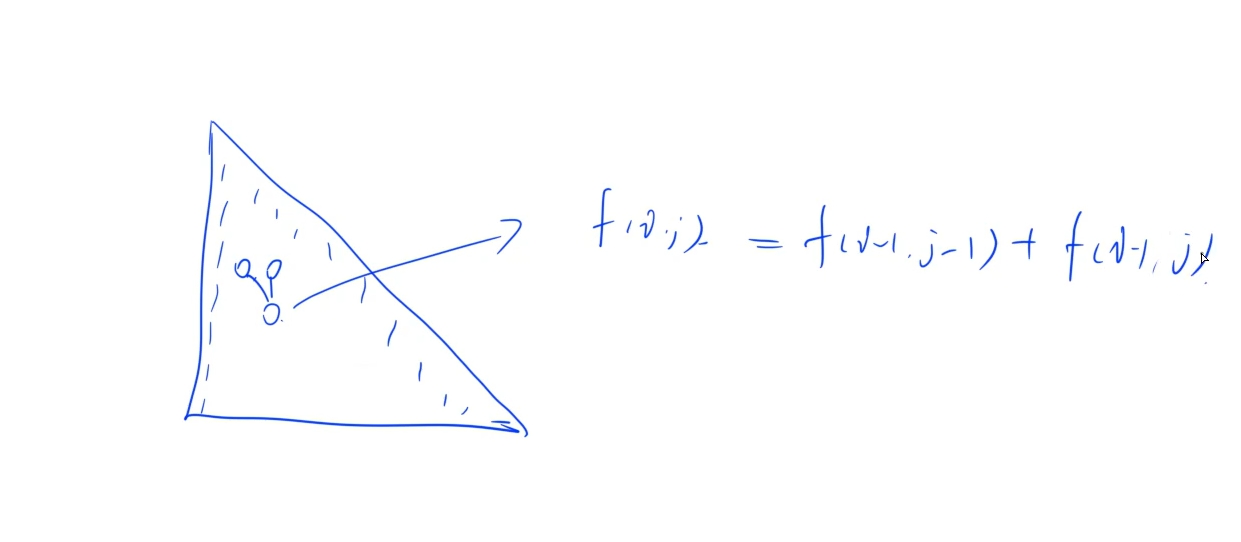
时间复杂度：

总共n行，每行最多n个数，总共n* (n + 1) / 2个数，每个数计算时间是O(1)的，总共的时间复杂度是O(n^2)的

注释代码：

class Solution {
public:vector<vector<int>> generate(int n) {vector<vector<int>> f;for(int i = 0; i < n; i++){vector<int> line(i + 1); //每一行的长度line[0] = line[i] = 1; //每一行的开头和结尾都是1for(int j = 1; j < i; j++)  //每一行的每个位置{line[j] = f[i - 1][j - 1] + f[i - 1][j]; //数为上一行同一列和上一行前一列的数之和}f.push_back(line);}return f;}
};

纯享版：

class Solution {
public:vector<vector<int>> generate(int n) {vector<vector<int>> res;for(int i = 0; i < n; i++){vector<int> line(i + 1);line[0] = line[i] = 1;for(int j = 1; j < i; j++){line[j] = res[i - 1][j] + res[i - 1][j - 1];}res.push_back(line);}return res;}
};

---

LeetCode119.杨辉三角Ⅱ：

题目描述：

给定一个非负索引 rowIndex，返回「杨辉三角」的第 rowIndex 行。

在「杨辉三角」中，每个数是它左上方和右上方的数的和。

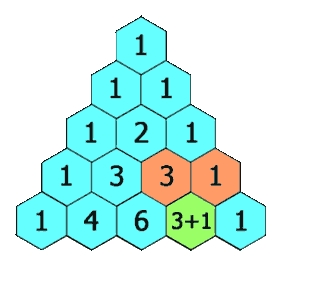
示例 1:

输入: rowIndex = 3
输出: [1,3,3,1]
示例 2:

输入: rowIndex = 0
输出: [1]

示例 3:

输入: rowIndex = 1
输出: [1,1]

提示:

0 <= rowIndex <= 33

进阶：

你可以优化你的算法到 O(rowIndex) 空间复杂度吗？

思路：

正常做法如下所示： 需要O(n*n)的空间复杂度， 进阶做法要求使用O(n)的空间复杂度，于是考虑使用滚动数组：
滚动数组：由于我们从状态方程f[i][j] = f[i - 1][j - 1] + f[i - 1][j]可以看出，当前行的状态只是跟上一行有关，所以在计算完当前行的状态值之后， 上一行的状态值就没用了，为了节省空间，我们只需要单开两行(为什么要两行？ 交替存储当前行的状态值，计算时不会发生冲突，奇数行和偶数行交替存储就不会发生覆盖问题)（怎么存储？ 将当前行区分为奇数行还是偶数行： (i % 2 == 0) -> i & 1: 如果当前行是奇数行，它的状态值就会存储到第0行，而利用上一行的状态值也就是偶数行（第一行）的值，以此交替

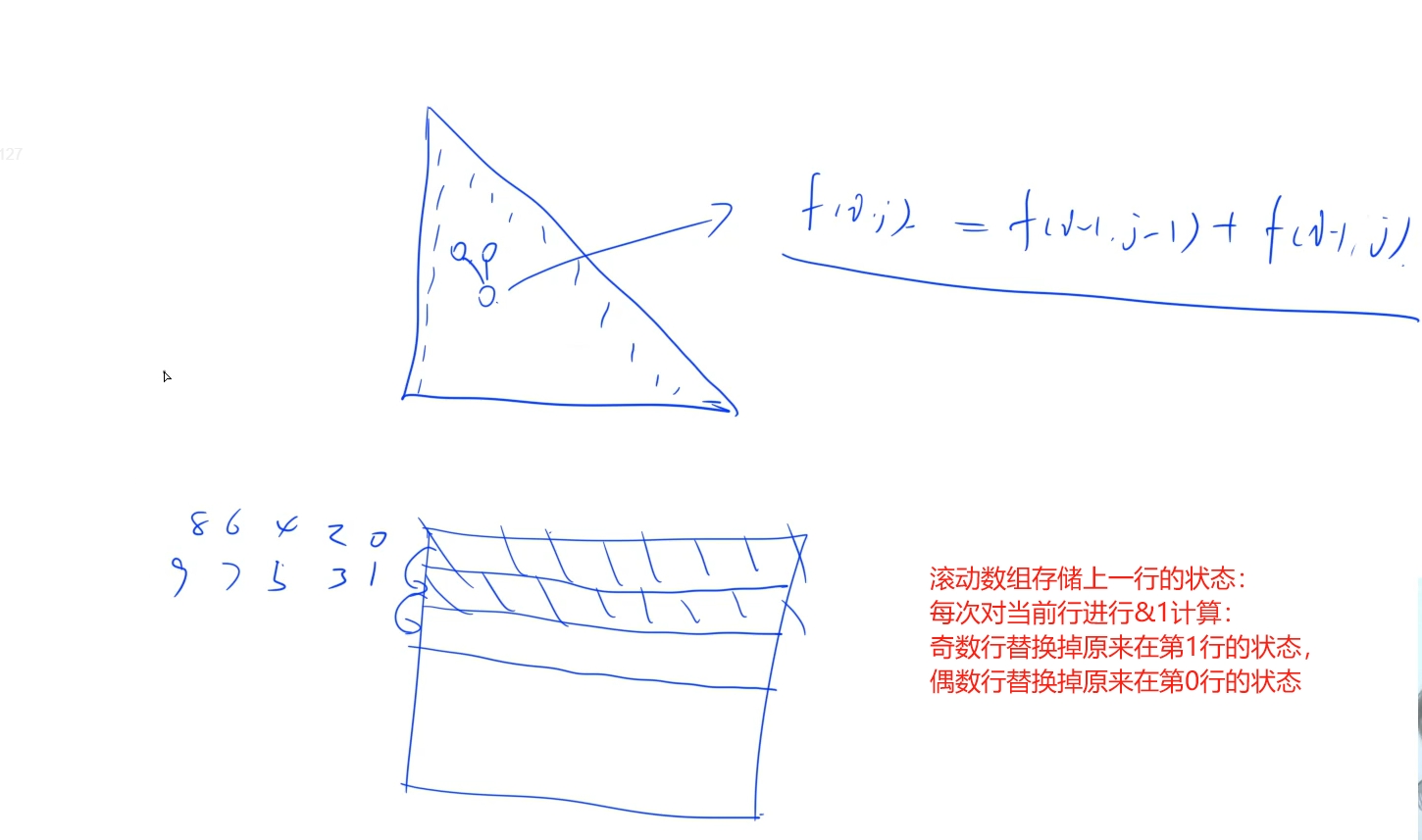
时间复杂度：

总共n层，总共：1 + 2 + …+n = n *(n + 1) / 2个数，每个数的计算时间是O(1)的，总共时间复杂度是O(n * n), 空间复杂度：总共开了2 * n个数组空间，2为常数，所以空间复杂度还是O(n)的

正常做法：

class Solution {
public:vector<int> getRow(int n) {vector<vector<int>> f(n + 1, vector<int> (n + 1));for(int i = 0; i <= n; i++){f[i][0] = f[i][i] = 1;for(int j = 1; j < i; j++){f[i][j] = f[i - 1][j - 1] + f[i - 1][j];}}return f[n];}
};

滚动数组：

class Solution {
public:vector<int> getRow(int n) {vector<vector<int>> f(2, vector<int> (n + 1));for(int i = 0; i <= n; i++){f[i & 1][0] = f[i & 1][i] = 1;for(int j = 1; j < i; j++){f[i & 1][j] = f[i - 1 & 1][j - 1] + f[i - 1 & 1][j];}}return f[n & 1];}
};

---

LeetCode120.三角形最小路径和：

题目描述：

给定一个三角形 triangle ，找出自顶向下的最小路径和。

每一步只能移动到下一行中相邻的结点上。相邻的结点 在这里指的是 下标 与 上一层结点下标 相同或者等于 上一层结点下标 + 1 的两个结点。也就是说，如果正位于当前行的下标 i ，那么下一步可以移动到下一行的下标 i 或 i + 1 。

示例 1：

输入：triangle = [[2],[3,4],[6,5,7],[4,1,8,3]]
输出：11
解释：如下面简图所示：
2
3 4
6 5 7
4 1 8 3
自顶向下的最小路径和为 11（即，2 + 3 + 5 + 1 = 11）。

示例 2：

输入：triangle = [[-10]]
输出：-10

提示：

1 <= triangle.length <= 200
triangle[0].length == 1
triangle[i].length == triangle[i - 1].length + 1
-10^4 <= triangle[i][j] <= 10^4

进阶：

你可以只使用 O(n) 的额外空间（n 为三角形的总行数）来解决这个问题吗？

思路：

最小路径和一看就是DP问题，但是有两种考虑方式：
1.从最下边往上：考虑最下边到上面任意元素的最下路径，边界条件比较多，一是要注意两边是否存在元素，二是需要判断路径是从哪个位置来的
2.从上往下：考虑每个位置到最底层的最小路径和：

时间复杂度：

每个位置会遍历到，总的时间复杂度为O(n*n), 空间复杂度：O(1):没有额外开空间，而是直接将元素位置的值改为当前位置到最底层的最小路径和

注释代码：

class Solution {
public:int minimumTotal(vector<vector<int>>& f) {for(int i = f.size()  - 2; i >= 0; i--){for(int j = 0; j <= i; j++){//f[i][j] 替换表示为：从（i, j) 到最底层的最小路径和f[i][j] += min(f[i + 1][j], f[i + 1][j + 1]);}}return f[0][0]; //返回最上面的点:也就是(0, 0)到最底层的最下路径和}
};

纯享版：

class Solution {
public:int minimumTotal(vector<vector<int>>& f) {for(int i = f.size() - 2; i >= 0; i--){for(int j = 0; j <= i; j++){f[i][j] += min(f[i + 1][j + 1], f[i + 1][j]);}}return f[0][0];}
};

---

LeetCode121.买卖股票的最佳时机：

题目描述：

给定一个数组 prices ，它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。

你只能选择 某一天 买入这只股票，并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。

返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润，返回 0 。

示例 1：

输入：[7,1,5,3,6,4]
输出：5
解释：在第 2 天（股票价格 = 1）的时候买入，在第 5 天（股票价格 = 6）的时候卖出，最大利润 = 6-1 = 5 。
注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格；同时，你不能在买入前卖出股票。

示例 2：

输入：prices = [7,6,4,3,1]
输出：0
解释：在这种情况下, 没有交易完成, 所以最大利润为 0。

提示：

1 <= prices.length <= 10^5
0 <= prices[i] <= 10^4

思路：

相当于上帝视角买股票：只要找到当前i之前最低的时机，每次比较当前i把股票卖出去赚的价值和之前卖股票赚的最大值，同时也要不断更新当前i之前的最低股票时机，取最小的股票时机

时间复杂度：

依次遍历每一天，每一天股票价格的计算也是O(1), 的所以总的时间消耗为O(n)

代码：

class Solution {
public:int maxProfit(vector<int>& prices) {int res = 0;for(int i = 0, minpr = INT_MAX; i < prices.size(); i++){res = max(res, prices[i] - minpr);minpr = min(minpr, prices[i]);}return res;}
};

---

LeetCode122.买卖股票的最佳时机Ⅱ：

题目描述：

给你一个整数数组 prices ，其中 prices[i] 表示某支股票第 i 天的价格。

在每一天，你可以决定是否购买和/或出售股票。你在任何时候 最多 只能持有 一股 股票。你也可以先购买，然后在 同一天 出售。

返回 你能获得的 最大 利润 。

示例 1：

输入：prices = [7,1,5,3,6,4]
输出：7
解释：在第 2 天（股票价格 = 1）的时候买入，在第 3 天（股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5 - 1 = 4。
随后，在第 4 天（股票价格 = 3）的时候买入，在第 5 天（股票价格 = 6）的时候卖出, 这笔交易所能获得利润 = 6 - 3 = 3。
最大总利润为 4 + 3 = 7 。

示例 2：

输入：prices = [1,2,3,4,5]
输出：4
解释：在第 1 天（股票价格 = 1）的时候买入，在第 5 天 （股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5 - 1 = 4。
最大总利润为 4 。

示例 3：

输入：prices = [7,6,4,3,1]
输出：0
解释：在这种情况下, 交易无法获得正利润，所以不参与交易可以获得最大利润，最大利润为 0。

提示：

1 <= prices.length <= 3 * 10^4
0 <= prices[i] <= 10^4

思路：

主要理解题意： 这题可以当天卖当天卖，而且不限制买卖次数，但手上只能持有一支股票，于是我们可以发现，只要即将有亏损就立马将股票卖出，能盈利的就立马买入：于是只要记录每两天之间是否增加，增就累计，减就不买：

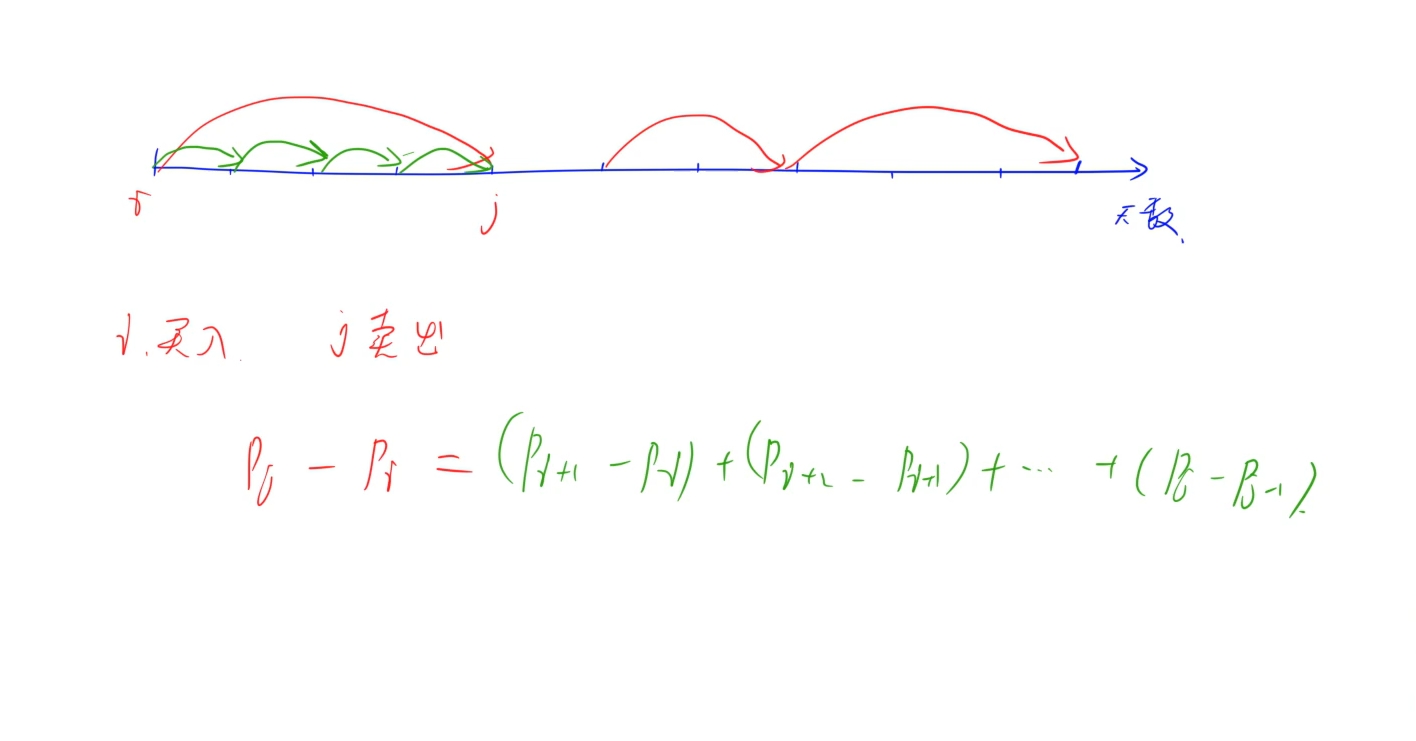
时间复杂度：

每天对比前一天的状态会计算一次，每次计算是O(1)的， 总共的时间消耗为O(n)

代码：

class Solution {
public:int maxProfit(vector<int>& prices) {int res = 0;for(int i = 0; i < prices.size() - 1; i++){res += max(0, prices[i + 1] - prices[i]);}return res;}
};

---

LeetCode123.买卖股票的最佳时机Ⅲ：

题目描述：

给定一个数组，它的第 i 个元素是一支给定的股票在第 i 天的价格。

设计一个算法来计算你所能获取的最大利润。你最多可以完成 两笔 交易。

注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

示例 1:

输入：prices = [3,3,5,0,0,3,1,4]
输出：6
解释：在第 4 天（股票价格 = 0）的时候买入，在第 6 天（股票价格 = 3）的时候卖出，这笔交易所能获得利润 = 3-0 = 3 。
随后，在第 7 天（股票价格 = 1）的时候买入，在第 8 天 （股票价格 = 4）的时候卖出，这笔交易所能获得利润 = 4-1 = 3 。

示例 2：

输入：prices = [1,2,3,4,5]
输出：4
解释：在第 1 天（股票价格 = 1）的时候买入，在第 5 天 （股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。
注意你不能在第 1 天和第 2 天接连购买股票，之后再将它们卖出。
因为这样属于同时参与了多笔交易，你必须在再次购买前出售掉之前的股票。

示例 3：

输入：prices = [7,6,4,3,1]
输出：0
解释：在这个情况下, 没有交易完成, 所以最大利润为 0。
示例 4：

输入：prices = [1]
输出：0

提示：

1 <= prices.length <= 10^5
0 <= prices[i] <= 10^5

思路：

两次！问题思路： 闫氏前后缀分解：将两次问题拆分开，看出两次的单独问题
比如这题： 我们以i为分界，将两次交易看作： 一次交易是在第i天买入，在i天之后卖出，那么另外一次交易就是在1~i-1天中买入和卖出，这样的话两次交易就不会有交错，同时两次都是需要取收益最大：
分段分析：
后一次交易比较简单： 如果在第i天买入，那么在第i天之后找到后面的最大值maxpr 卖出就一定是当前交易收益的最大值：res = maxpr - price[i]
前一次交易： 在1 ~ i- 1天中交易一次获取交易最大值，跟 买卖股票的最佳时机 一致，当然也可以看成是一个简单DP问题： 设定集合f[i]表示为在1~i天中买入和卖出一次的收益最大值，那么可以分为在第i天卖出和不在第i天卖出： 首先维护当前i之前的最小价格minpr：
第i天卖出： prices[i] - minpr
不在第i天卖出，那么就表示需要在1 ~ i- 1天中买入和卖出一次，状态表示为f[i - 1]
最终这一次交易的最大收益就为max(f[i - 1], prices[i] - minpr)

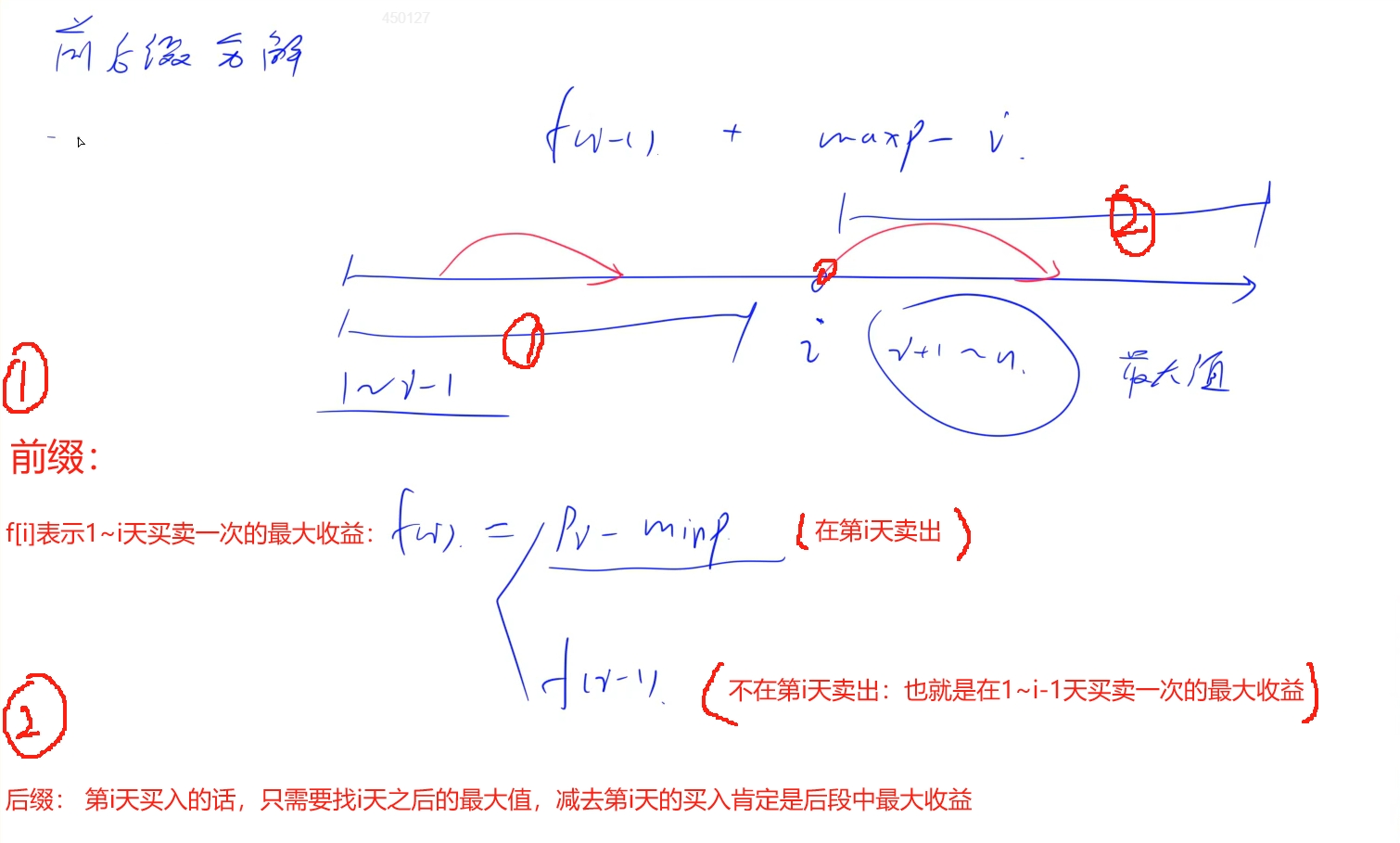
时间复杂度：

两次交易均遍历一遍prices数组，每个元素遍历两次，所以总的时间复杂度还是O(n)的

注释代码：

class Solution {
public:int maxProfit(vector<int>& prices) {int n = prices.size(); //天数vector<int> f(n + 2);//将两次的交易拆分//将交易第一次： 1~i中买入和卖出一次的最大收益//求出f[i]: 在1~i天中买入和卖出一次的最大收益//从1开始，因为涉及到f[i - 1]，0的话会越界，所以将prices向后移一位，f[i] 不变for(int i = 1, minpr = INT_MAX; i <= n; i++){f[i] = max(f[i - 1], prices[i - 1] - minpr);minpr = min(minpr, prices[i - 1]);}int res = 0;  //第二次交易是第i天买入，在之后某天卖出//从后往前找到i之后的最大值//因为上面移了一位，所以整体向后移一位for(int i = n, maxpr = 0; i > 0; i--){cout<<i<<endl;res = max(res, maxpr - prices[i - 1] + f[i - 1]); //二次交易加在一起的最大收益maxpr = max(maxpr, prices[i - 1]); //更新i之后的最大价格}return res;}
};

纯享版：

class Solution {
public:int maxProfit(vector<int>& prices) {int n = prices.size();vector<int> f(n + 2);for(int i = 1, minpr = INT_MAX; i <= n; i++){f[i] = max(f[i - 1], prices[i - 1] - minpr);minpr = min(minpr, prices[i - 1]);}int res = 0;for(int i = n, maxpr = 0; i > 0; i--){res = max(res, maxpr - prices[i - 1] + f[i - 1]);maxpr = max(maxpr, prices[i - 1]);}return res;}
};

---

LeetCode124.二叉树的最大路径和：

题目描述：

二叉树中的 路径 被定义为一条节点序列，序列中每对相邻节点之间都存在一条边。同一个节点在一条路径序列中 至多出现一次 。该路径 至少包含一个 节点，且不一定经过根节点。

路径和 是路径中各节点值的总和。

给你一个二叉树的根节点 root ，返回其 最大路径和 。

示例 1：

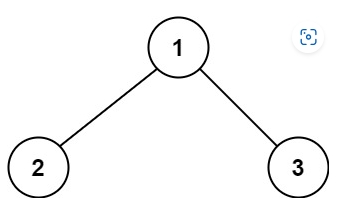
输入：root = [1,2,3]
输出：6
解释：最优路径是 2 -> 1 -> 3 ，路径和为 2 + 1 + 3 = 6

示例 2：

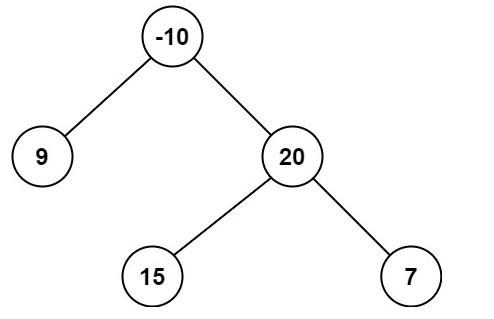
输入：root = [-10,9,20,null,null,15,7]
输出：42
解释：最优路径是 15 -> 20 -> 7 ，路径和为 15 + 20 + 7 = 42

提示：

树中节点数目范围是 [1, 3 * 10^4]
-1000 <= Node.val <= 1000

思路：

最大路径并且可以不包含根节点，那么也就是需要搜索每一条路径，两个节点之间都存在路径，常用树的路径搜索方式： 枚举每个节点，考虑以该节点为最高节点(相连)下的所有路径（如图所示），这样的总和就可以找出所有路径

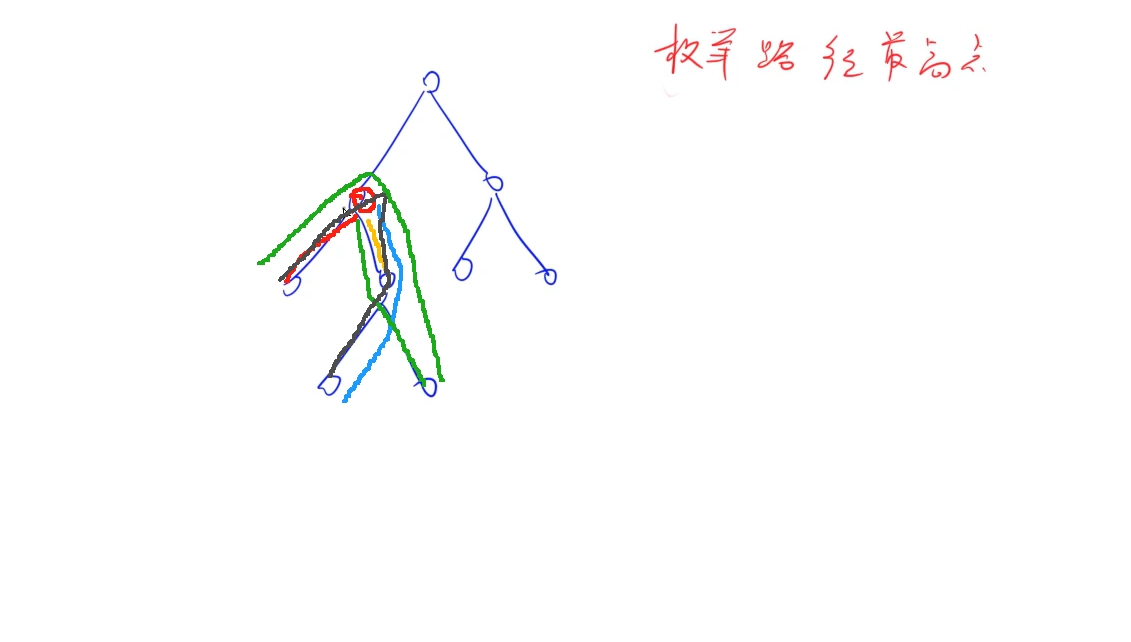
每条路径找到了，接下来的问题就是如何在这些路径中找到最大的路径和，首先统计以每个节点为最高点下的路径中路径和的最大值，以某个节点为顶点求其下面的最大值，类似于之前的求根节点下的最大值，做法就是： 获取到左儿子下的路径最大值和右儿子下的路径最大值，那么以当前节点为最高点的路径和最大值就是当前节点值+ 左儿子下路径最大值（大于零的前提下）+右儿子下路径最大值（大于0的前提下），而为了求左右儿子下的路径最大值，深搜无疑是最好的方式，使用dfs，每次找到当前节点下的左儿子和右儿子的最大路径和，当前节点最大路径和就为当前节点值+max(左儿子最大路径和， 右儿子最大路径和),以此往下搜即可

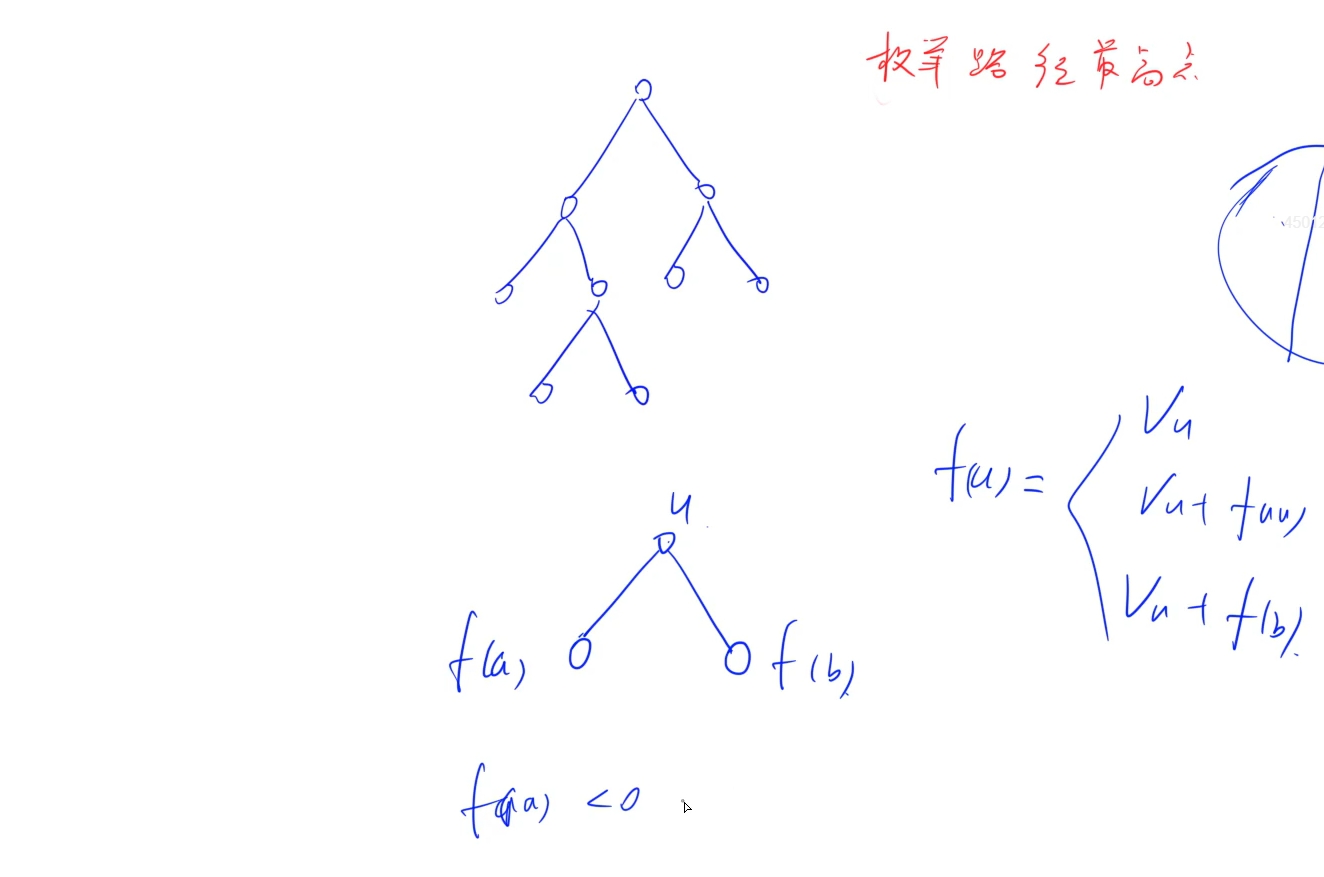
时间复杂度：

每个节点搜一次，每次计算时间为O(1),总的时间复杂度为O(n)

注释代码：

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:int ans;int maxPathSum(TreeNode* root) {ans = INT_MIN;dfs(root);  //返回以当前节点为最高点下的最大路径和return ans;}int dfs(TreeNode* u)  {if(!u) return 0;int left = max(0, dfs(u -> left));  //返回左边节点下的最大路径和int right = max(0, dfs(u -> right)); //返回右边节点下的最大路径和ans = max(ans, u -> val + left + right); //答案是在每次节点下左右节点连通之和return u -> val + max(left, right);  //当前节点下的最大路径和为： 当前节点值与max(左边节点，右边节点)最大路径}
};

纯享版：

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:int res;int maxPathSum(TreeNode* root) {res = INT_MIN;dfs(root);return res;}int dfs(TreeNode* u){if(!u) return 0;int l = max(0, dfs(u -> left));int r = max(0, dfs(u -> right));res = max(res, u -> val + l + r);return u -> val + max(l , r);}
};

---

LeetCode125.验证回文串：

题目描述：

如果在将所有大写字符转换为小写字符、并移除所有非字母数字字符之后，短语正着读和反着读都一样。则可以认为该短语是一个 回文串 。

字母和数字都属于字母数字字符。

给你一个字符串 s，如果它是 回文串 ，返回 true ；否则，返回 false 。

示例 1：

输入: s = “A man, a plan, a canal: Panama”
输出：true
解释：“amanaplanacanalpanama” 是回文串。

示例 2：

输入：s = “race a car”
输出：false
解释：“raceacar” 不是回文串。

示例 3：

输入：s = " "
输出：true
解释：在移除非字母数字字符之后，s 是一个空字符串 “” 。
由于空字符串正着反着读都一样，所以是回文串。

提示：

1 <= s.length <= 2 * 10^5
s 仅由可打印的 ASCII 字符组成

tolower函数： 可以将大写字母转成小写字母，小写字母则原样输出

思路：

双指针： 头尾分别使用两个指针，只要不是大小写字母或者数字字符就往中间跳

时间复杂度：s.length是2 * 10^5，使用O(n)的双指针算法

代码：

class Solution {
public:bool check(char c){return c >= 'a' && c <= 'z' || c >= 'A' && c <= 'Z'|| c >= '0' && c <= '9';}bool isPalindrome(string s) {for(int i = 0, j = s.size() - 1; i < j; i++, j--){while(i < j && !check(s[i])) i++;while(i < j && !check(s[j])) j--;if(i < j && tolower(s[i]) != tolower(s[j])) return false;}return true;}
};

---

LeetCode126.单词接龙Ⅱ：

题目描述：

按字典 wordList 完成从单词 beginWord 到单词 endWord 转化，一个表示此过程的 转换序列 是形式上像 beginWord -> s1 -> s2 -> … -> sk 这样的单词序列，并满足：

每对相邻的单词之间仅有单个字母不同。
转换过程中的每个单词 si（1 <= i <= k）必须是字典 wordList 中的单词。注意，beginWord 不必是字典 wordList 中的单词。
sk == endWord
给你两个单词 beginWord 和 endWord ，以及一个字典 wordList 。请你找出并返回所有从 beginWord 到 endWord 的 最短转换序列 ，如果不存在这样的转换序列，返回一个空列表。每个序列都应该以单词列表 [beginWord, s1, s2, …, sk] 的形式返回。

示例 1：

输入：beginWord = “hit”, endWord = “cog”, wordList = [“hot”,“dot”,“dog”,“lot”,“log”,“cog”]
输出：[[“hit”,“hot”,“dot”,“dog”,“cog”],[“hit”,“hot”,“lot”,“log”,“cog”]]
解释：存在 2 种最短的转换序列：
“hit” -> “hot” -> “dot” -> “dog” -> “cog”
“hit” -> “hot” -> “lot” -> “log” -> “cog”

示例 2：

输入：beginWord = “hit”, endWord = “cog”, wordList = [“hot”,“dot”,“dog”,“lot”,“log”]
输出：[]
解释：endWord “cog” 不在字典 wordList 中，所以不存在符合要求的转换序列。

提示：

1 <= beginWord.length <= 5
endWord.length == beginWord.length
1 <= wordList.length <= 500
wordList[i].length == beginWord.length
beginWord、endWord 和 wordList[i] 由小写英文字母组成
beginWord != endWord
wordList 中的所有单词 互不相同

思路：

使用图论知识，将开始单词到结束单词的所有单词看成一个点，两个单词之间的变换就是边权为1的边，
从开始单词beginWord开始，不断往后判断当前单词(点t)能否由上一个单词(点r)变换一次(dist[t] == dist[r] + 1)得到，最后变换得到endWord为止
dist存储当前点到起点的距离,由于题意需要求所有从beginWord到endWord的最短路径，于是变成图的最短路问题

时间复杂度：

注释代码：

class Solution {
public:unordered_set<string> S;   unordered_map<string, int> dist;queue<string> q;vector<vector<string>> ans;vector<string> path;string beginWord;vector<vector<string>> findLadders(string _beginWord, string endWord, vector<string>& wordList) {for(auto word : wordList)  S.insert(word);beginWord = _beginWord;dist[beginWord] = 0;q.push(beginWord); //将开始单词加入while(q.size()){auto t = q.front(); //拿出队头q.pop();string r = t;  //记录队头防止丢失for(int i = 0; i < t.size(); i++)  //对于每一个单词的每一位{t = r; //重新置为原始的队头单词，不让上一个字母的改变影响下一个字母的改变for(char j = 'a'; j <= 'z'; j++)  //要将当前为变成哪个字母{t[i] = j; //将其中一个字母换掉if(S.count(t) && dist.count(t) == 0)  //如果能在字典中找到并且没有出现过{dist[t] = dist[r] + 1;  //建一条边，说明字典中的这个单词到队头单词的改变距离为1if(t == endWord) break;  //如果换完的单词为结束单词，说明已经找完了，breakq.push(t);  //不然的话将换完的单词放到队列中}}}}if(dist.count(endWord) == 0) return ans;  //如果dist中没有终点，就不用搜索了path.push_back(endWord); //将终点插入路径dfs(endWord);//从终点开始深度搜索return ans;}void dfs(string t){if(t == beginWord) //搜到开始单词的话就意味着搜到了一条路径{reverse(path.begin(), path.end());  //翻转一下ans.push_back(path); //放入答案集合reverse(path.begin(), path.end());  //翻转回来，防止下一次dfs乱序}else{string r = t; for(int i = 0; i < t.size(); i++) //看当前t可以从哪些边过来{t = r;for(char j = 'a'; j <= 'z'; j++){t[i] = j;if(dist.count(t) && dist[t] + 1 == dist[r]) //如果存在这条边，并且能走到新的t{path.push_back(t);  //就将当前的t加入路径中dfs(t);//并继续搜索t的下一个边path.pop_back(); //恢复现场}}}}}
};

纯享版：

class Solution {
public:unordered_map<string, int> dist;vector<vector<string>> res;vector<string> path;unordered_set<string> S;string beginWord;queue<string> q;vector<vector<string>> findLadders(string _beginWord, string endWord, vector<string>& wordList) {for(auto word : wordList) S.insert(word);beginWord = _beginWord;dist[beginWord] = 0;q.push(beginWord);while(q.size()){string t = q.front();q.pop();string r = t;for(int i = 0; i < t.size(); i++){t = r;for(char j = 'a'; j <= 'z'; j++){t[i] = j;if(S.count(t) && dist.count(t) == 0){dist[t] = dist[r] + 1;cout<<t<<' ' <<r<<' ';if(t == endWord) break;q.push(t);}}}}if(dist.count(endWord) == 0) return res;path.push_back(endWord);dfs(endWord);return res;}void dfs(string t){if(t == beginWord){reverse(path.begin(), path.end());res.push_back(path);reverse(path.begin(), path.end());}else{string r = t;for(int i = 0; i < t.size(); i++){t = r;for(char j = 'a'; j <= 'z'; j++){t[i] = j;if(dist.count(t) && dist[t]  + 1 == dist[r]){path.push_back(t);dfs(t);path.pop_back();}}}}}
};

---

LeetCode127.单词接龙：

题目描述：

字典 wordList 中从单词 beginWord 到 endWord 的 转换序列 是一个按下述规格形成的序列 beginWord -> s1 -> s2 -> … -> sk：

每一对相邻的单词只差一个字母。
对于 1 <= i <= k 时，每个 si 都在 wordList 中。注意， beginWord 不需要在 wordList 中。
sk == endWord
给你两个单词 beginWord 和 endWord 和一个字典 wordList ，返回 从 beginWord 到 endWord 的 最短转换序列 中的 单词数目 。如果不存在这样的转换序列，返回 0 。

示例 1：

输入：beginWord = “hit”, endWord = “cog”, wordList = [“hot”,“dot”,“dog”,“lot”,“log”,“cog”]
输出：5
解释：一个最短转换序列是 “hit” -> “hot” -> “dot” -> “dog” -> “cog”, 返回它的长度 5。

示例 2：

输入：beginWord = “hit”, endWord = “cog”, wordList = [“hot”,“dot”,“dog”,“lot”,“log”]
输出：0
解释：endWord “cog” 不在字典中，所以无法进行转换。

提示：

1 <= beginWord.length <= 10
endWord.length == beginWord.length
1 <= wordList.length <= 5000
wordList[i].length == beginWord.length
beginWord、endWord 和 wordList[i] 由小写英文字母组成
beginWord != endWord
wordList 中的所有字符串 互不相同

思路：

建图： 根据单词之间的变换关系，建立每个单词到beginWord的变换操作次数，dist存储当前单词（节点）跟开始单词（起点）的距离，通过不断构建两点之间的边，最后找到结束单词endWord时返回endWord距离开始单词的距离即可（当然要加1， 因为起点设置的距离为0， 但是题意要求返回包括begin Word在内的长度）

时间复杂度：

注释代码：

class Solution {
public:int ladderLength(string beginWord, string endWord, vector<string>& wordList) {unordered_set<string> S;for(auto word : wordList) S.insert(word);queue<string> q;unordered_map<string, int> dist;dist[beginWord] = 0;q.push(beginWord);while(q.size()){string t = q.front();q.pop();string r = t;for(int i = 0; i < t.size(); i++){t = r;for(char j = 'a'; j <= 'z'; j++){t[i] = j;if(S.count(t) && dist.count(t) == 0){dist[t] = dist[r] + 1;if(t == endWord) return dist[t] + 1; //dist数组就是表示当前单词跟开始单词的距离，由于dist[beginWord]是0开始，所以+1q.push(t);}}}}return 0;}
};

纯享版：

class Solution {
public:int ladderLength(string beginWord, string endWord, vector<string>& wordList) {unordered_set<string> S;for(auto word : wordList) S.insert(word);unordered_map<string, int> dist;queue<string> q;dist[beginWord] = 0;q.push(beginWord);while(q.size()){string t = q.front();q.pop();string r = t;for(int i = 0; i < t.size(); i++){t = r;for(char j = 'a'; j <= 'z'; j++){t[i] = j;if(S.count(t) && dist.count(t) == 0) {dist[t] = dist[r] + 1;if(t == endWord) return dist[t] + 1;q.push(t);}}}}return 0;}
};

---

LeetCode128.最长连续序列：

题目描述：

给定一个未排序的整数数组 nums ，找出数字连续的最长序列（不要求序列元素在原数组中连续）的长度。

请你设计并实现时间复杂度为 O(n) 的算法解决此问题。

示例 1：

输入：nums = [100,4,200,1,3,2]
输出：4
解释：最长数字连续序列是 [1, 2, 3, 4]。它的长度为 4。

示例 2：

输入：nums = [0,3,7,2,5,8,4,6,0,1]
输出：9

提示：

0 <= nums.length <= 10^5
-10^9 <= nums[i] <= 10^9

思路：

将全部元素插入哈希表中，然后遍历查找数组元素，先找到起点： 没有前面一个数 再找到终点： 没有后面的一个数，计算两者中间的长度，然后取最大

时间复杂度：题目要求O(n)

注释代码：

class Solution {
public:int longestConsecutive(vector<int>& nums) {unordered_set<int> S;for(auto x : nums) S.insert(x);int res = 0;for(auto x : nums){if(S.count(x) && !S.count(x -1))  //起点:前面没有元素的话{int y = x;S.erase(x);  //找到起点后移除，防止重复查找while(S.count(y + 1))  //终点： 往后移动，直到后面没有元素{y++;S.erase(y); //}res = max(res, y - x + 1);}}return res;}
};

纯享版：

class Solution {
public:int longestConsecutive(vector<int>& nums) {unordered_set<int> hash;for(auto x : nums) hash.insert(x);int res = 0;for(auto x : nums){if(hash.count(x) && !hash.count(x -1)){int y = x;hash.erase(x);while(hash.count(y + 1)){y++;hash.erase(y);}res = max(res, y - x + 1);}}return res;}
};

---

LeetCode129.求根到叶子节点数字之和：

题目描述：

给你一个二叉树的根节点 root ，树中每个节点都存放有一个 0 到 9 之间的数字。
每条从根节点到叶节点的路径都代表一个数字：

例如，从根节点到叶节点的路径 1 -> 2 -> 3 表示数字 123 。
计算从根节点到叶节点生成的 所有数字之和 。

叶节点 是指没有子节点的节点。

示例 1：

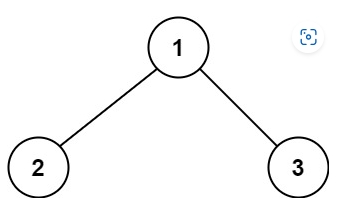
输入：root = [1,2,3]
输出：25
解释：
从根到叶子节点路径 1->2 代表数字 12
从根到叶子节点路径 1->3 代表数字 13
因此，数字总和 = 12 + 13 = 25

示例 2：

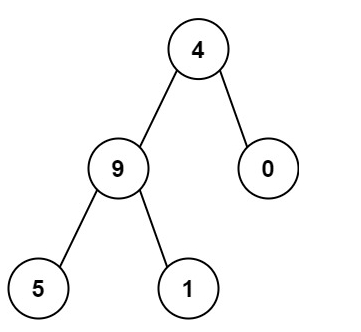
输入：root = [4,9,0,5,1]
输出：1026
解释：
从根到叶子节点路径 4->9->5 代表数字 495
从根到叶子节点路径 4->9->1 代表数字 491
从根到叶子节点路径 4->0 代表数字 40
因此，数字总和 = 495 + 491 + 40 = 1026

提示：

树中节点的数目在范围 [1, 1000] 内
0 <= Node.val <= 9
树的深度不超过 10

思路：

老生常谈的做法了，怎么一直不会用？ 涉及树的从根到叶子节点的问题一般只需要考虑局部，就以任意一个节点u以及它的左儿子a， 右儿子b来说，当前u的值可以表示为上面传下来的number* 10 + 自身节点值，同时呢将这个值传下去，以此往下推，直到叶子节点则将所有叶子节点下的值累加到一起就是我们的答案

时间复杂度：每个节点搜索一次， 每个节点number的计算时间是O(1)的，总的时间复杂度是O(n)的

注释代码：

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:int res = 0;int sumNumbers(TreeNode* root) {if(root) dfs(root, 0); //从根节点往下搜return res;}void dfs(TreeNode* root, int number){number = number * 10 + root -> val;  //当前节点值等于父节点的值*10 + 自身节点值if(!root -> left && !root -> right) res += number;  //如果是叶子节点，那么加上这条路径上的总值if(root -> left) dfs(root -> left, number);  //往左儿子搜if(root -> right) dfs(root -> right, number); //往右儿子搜}
};

纯享版：

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:int res = 0;int sumNumbers(TreeNode* root) {if(root) dfs(root, 0);return res;}void dfs(TreeNode* root, int number){number = number * 10 + root -> val;if(!root -> left  && !root -> right) res += number;if(root -> left) dfs(root -> left, number);if(root -> right) dfs(root -> right, number);}
};

---

LeetCode130.被围绕的区域：

题目描述：

给你一个 m x n 的矩阵 board ，由若干字符 ‘X’ 和 ‘O’ 组成，捕获 所有 被围绕的区域：

连接：一个单元格与水平或垂直方向上相邻的单元格连接。
区域：连接所有 ‘O’ 的单元格来形成一个区域。
围绕：如果您可以用 ‘X’ 单元格 连接这个区域，并且区域中没有任何单元格位于 board 边缘，则该区域被 ‘X’ 单元格围绕。
通过将输入矩阵 board 中的所有 ‘O’ 替换为 ‘X’ 来 捕获被围绕的区域。

示例 1：

输入：board = [[“X”,“X”,“X”,“X”],[“X”,“O”,“O”,“X”],[“X”,“X”,“O”,“X”],[“X”,“O”,“X”,“X”]]

输出：[[“X”,“X”,“X”,“X”],[“X”,“X”,“X”,“X”],[“X”,“X”,“X”,“X”],[“X”,“O”,“X”,“X”]]

解释：

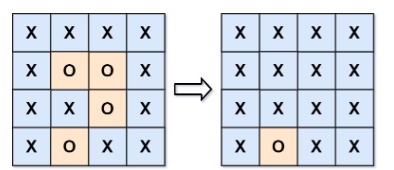
在上图中，底部的区域没有被捕获，因为它在 board 的边缘并且不能被围绕。

示例 2：

输入：board = [[“X”]]

输出：[[“X”]]

提示：

m == board.length
n == board[i].length
1 <= m, n <= 200
board[i][j] 为 ‘X’ 或 ‘O’

思路：

利用逆向思维：题目要求将所有连通的围绕O区域换成X，那么我们可以先找到所有没有被围绕也就是与边界相连或者在边界上的O并替换成#标记出来，通过遍历将这些区域换回O，而其他的则全部为X：

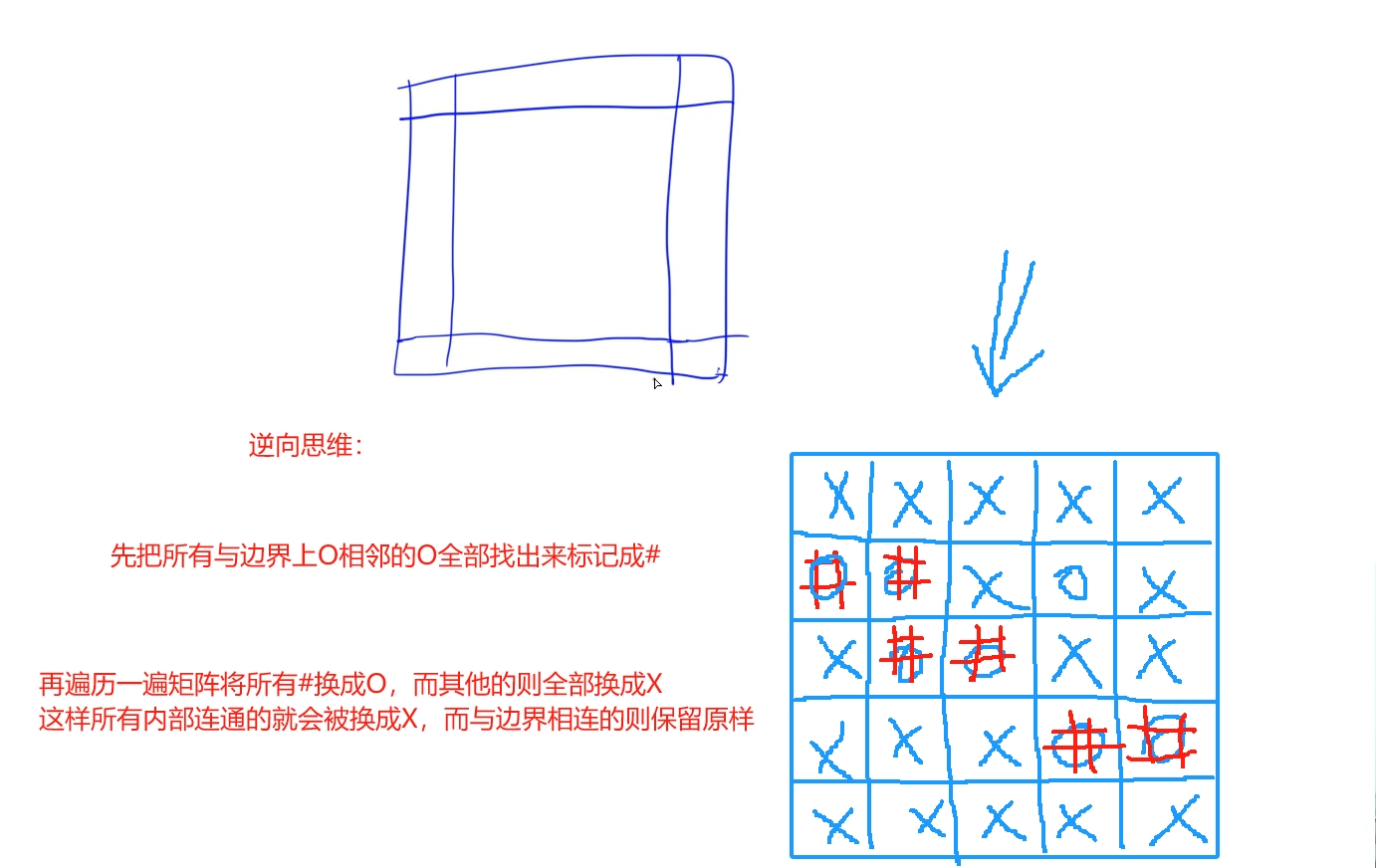
时间复杂度：

每个位置仅被遍历一次，所以时间复杂度是 O(nm)

注释代码：

class Solution {
public:int n, m;vector<vector<char>> board;int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};void solve(vector<vector<char>>& _board) {board = _board;n = board.size();if(!n) return;m =  board[0].size();for(int i = 0; i < n; i++) //第一列和最后一列有为O的话，将与该O相连的所有O找出来，标记{if(board[i][0] == 'O') dfs(i, 0);if(board[i][m - 1] == 'O') dfs(i, m - 1);}for(int i = 0; i < m; i++)  //第一行和最后一行有为O的话，将与该O相连的所有O找出来，标记{if(board[0][i] == 'O') dfs(0, i);if(board[n - 1][i] == 'O') dfs(n - 1, i);}for(int i = 0;i < n; i++){for(int j = 0; j < m; j++){if(board[i][j] == '#') board[i][j] = 'O'; //将所有与边缘相连的格子也就是标记为#的格子替换成Oelse board[i][j] = 'X';  //否则替换成X}}_board = board;}void dfs(int x, int y){board[x][y] = '#';  //将当前格子替换成#for(int i = 0; i < 4; i++){int a = x + dx[i], b = y + dy[i];if(a >= 0 && a < n && b >= 0 && b < m && board[a][b] == 'O')  //找到所有连在一起的O{dfs(a, b); //继续找下一个格子}}}
};

纯享版：

class Solution {
public:vector<vector<char>> board;int n, m;int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};void solve(vector<vector<char>>& _board) {board = _board;n = board.size();if(!n) return;m = board[0].size();for(int i = 0; i < n; i++){if(board[i][0] == 'O') dfs(i, 0);if(board[i][m - 1] == 'O') dfs(i, m - 1);}for(int i = 0; i < m; i++){if(board[0][i] == 'O') dfs(0, i);if(board[n - 1][i] == 'O') dfs(n - 1, i);}for(int i = 0; i < n; i++){for(int j = 0; j < m; j++){if(board[i][j] == '#') board[i][j] = 'O';else board[i][j] = 'X';}}_board = board;}void dfs(int x, int y){board[x][y] = '#';for(int i = 0; i < 4; i++){int a = x + dx[i], b = y + dy[i];if(a >= 0 && a < n && b >= 0 && b < m && board[a][b] == 'O'){dfs(a, b);}}}
};

2024/12/27二刷：

class Solution {
public:vector<vector<char>> board;int n, m;int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, -1, 0, 1};void solve(vector<vector<char>>& _board) {board = _board;n = board.size(), m = board[0].size();for(int i = 0; i < n; i++)  //第一列和最后一列的边缘连通块{if(board[i][0] == 'O') dfs(i, 0);if(board[i][m - 1] == 'O') dfs(i, m - 1);}for(int i = 0; i < m; i++)  //第一行和最后一行的边缘连通块{if(board[0][i] == 'O') dfs(0, i);if(board[n - 1][i] == 'O') dfs(n - 1, i);}for(int i = 0; i < n; i++){for(int j = 0; j < m; j++){if(board[i][j] == '#') board[i][j] = 'O';  //将边缘的连通块保留下来else board[i][j] = 'X';  //其他连通块填成X}}_board = board;}void dfs(int x, int y)  //找到以x,y为起点的连通块{board[x][y] = '#';for(int i = 0; i < 4; i++){int a = x + dx[i], b = y + dy[i];if(a >= 0 && a < n && b >= 0 && b < m && board[a][b] == 'O'){dfs(a, b);}}}
};

*注：上述题解均来自acwing课程讲解截图，仅作为学习交流，不作为商业用途，如有侵权，联系删除。