0 序言

本文为NumPy数组库的系统学习笔记，将自己先前的笔记做一个总结归纳。内容涵盖数组基础、创建、索引、变形、运算、函数、布尔型数组及与张量的衔接等内容。通过具体示例解析核心概念与操作，帮助读者掌握NumPy的使用逻辑与方法，为后续深度学习中数据处理打下基础，读完可独立完成数组的创建、操作及与张量的转换。

使用的Python版本为3.12
NumPy版本为2.2.4
代码编辑器为VsCode

1 数组基础

数组作为NumPy的核心数据结构，其基础特性直接决定了后续复杂操作的实现逻辑。要熟练运用NumPy数组，首先需要掌握其最根本的属性——数据类型与维度。

数据类型决定了数组中元素的存储形式和运算规则，整数型与浮点型数组的区分、元素插入时的同化特性，以及类型间的转换方法，是保证数据处理准确性的基础；

而数组的维度（如一维向量与二维矩阵）则影响着数据的组织形式和操作方式，理解维度的表示、形状参数及不同维度间的转换，是进行数组索引、变形等操作的前提。

接下来，我们将从数据类型和数组维度两方面，详细解析NumPy数组的基础特性。

1.1 数据类型

1.1.1 整数型与浮点型数组

整数型数组：元素均为整数，如arr1 = np.array([1, 2, 3])，输出[1 2 3]。
浮点型数组：含浮点数，如arr2 = np.array([1.0, 2, 3])，输出[1. 2. 3.]。
区别：print输出时，浮点型元素带小数点，整数型不带。

1.1.2 同化特性

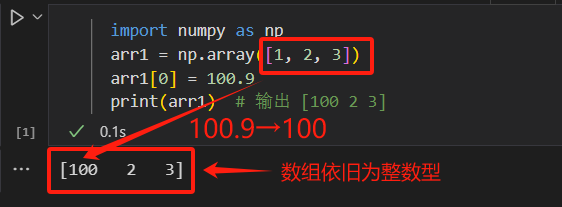
往整数型数组插入浮点数，浮点数自动截断为整数，数组仍为整数型。
```
import numpy as np
arr1 = np.array([1, 2, 3])
arr1[0] = 100.9
print(arr1)  
```

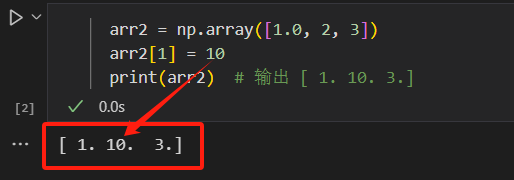
在这里插入图片描述

往浮点型数组插入整数，整数自动升级为浮点数，数组仍为浮点型。
```
arr2 = np.array([1.0, 2, 3])
arr2[1] = 10
print(arr2)  # 输出 [ 1. 10. 3.]
```

在这里插入图片描述

1.1.3 相互改变特性

整数型与浮点型数组相互转换的规范方法：使用.astype()方法。

arr1 = np.array([1, 2, 3])
arr2 = arr1.astype(float)  # 整数型转浮点型，输出 [1. 2. 3.]
arr3 = arr2.astype(int)    # 浮点型转整数型，输出 [1 2 3]

整数型数组可通过运算升级为浮点型数组（浮点型数组运算一般不降级）。

arr = np.array([1, 2, 3])
print(arr + 0.0)  # 输出 [1. 2. 3.]
print(arr / 1)    # 输出 [1. 2. 3.]

1.2 数组维度

1.2.1 一维与二维数组

显示区别：一维数组用1层中括号表示；二维数组用2层中括号表示。

形状参数：一维数组形如(x,)；二维数组形如(x,y)。

arr1 = np.ones(3)       # 一维数组，形状 (3,)，输出 [1. 1. 1.]
arr2 = np.ones((1,3))   # 二维数组，形状 (1,3)，输出 [[1. 1. 1.]]

维度查看：通过.shape属性，如print(arr1.shape)输出(3,)，print(arr2.shape)输出(1, 3)。

1.2.2 不同维度数组的转换

转换方法：使用.reshape()方法，可通过-1让系统自动计算维度。

一维转二维：

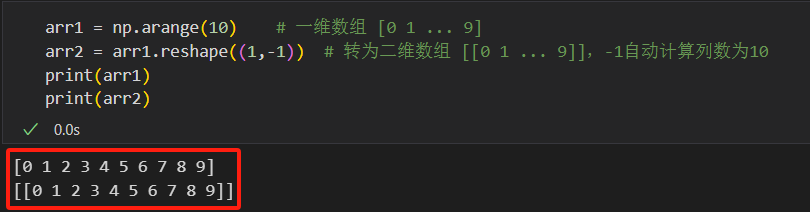
arr1 = np.arange(10)    # 一维数组 [0 1 ... 9]
arr2 = arr1.reshape((1,-1))  # 转为二维数组 [[0 1 ... 9]]，-1自动计算列数为10

在这里插入图片描述

二维转一维：

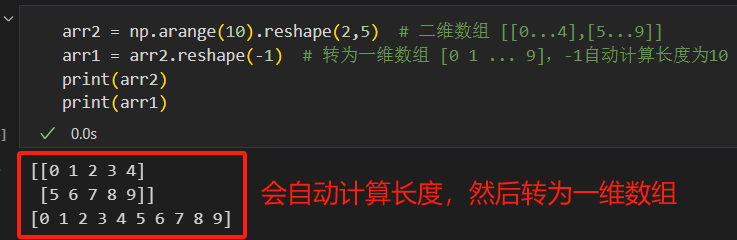
arr2 = np.arange(10).reshape(2,5)  # 二维数组 [[0...4],[5...9]]
arr1 = arr2.reshape(-1)  # 转为一维数组 [0 1 ... 9]，-1自动计算长度为10

注意：一维数组称为向量，二维数组称为矩阵。

在这里插入图片描述

2 数组的创建

2.1 创建指定数组

方法：使用np.array()函数，将Python列表转换为NumPy数组。

程序示例：

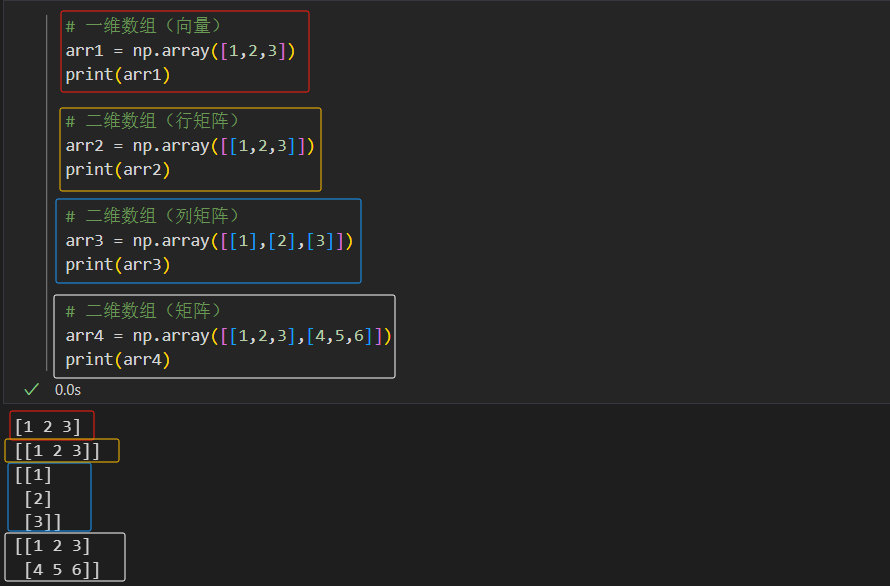
# 一维数组（向量）
arr1 = np.array([1,2,3])
print(arr1)  # 输出 [1 2 3]# 二维数组（行矩阵）
arr2 = np.array([[1,2,3]])
print(arr2)  # 输出 [[1 2 3]]# 二维数组（列矩阵）
arr3 = np.array([[1],[2],[3]])
print(arr3)  # 输出 [[1] [2] [3]]# 二维数组（矩阵）
arr4 = np.array([[1,2,3],[4,5,6]])
print(arr4)  # 输出 [[1 2 3] [4 5 6]]

在这里插入图片描述

2.2 创建递增数组

方法：使用np.arange()函数（全称array_range）。

程序示例：

# 从0开始，到10之前结束
arr1 = np.arange(10)
print(arr1)  # 输出 [0 1 ... 9]# 从10开始，到20之前结束
arr2 = np.arange(10,20)
print(arr2)  # 输出 [10 11 ... 19]# 从1开始，到21之前结束，步长为2
arr3 = np.arange(1,21,2)
print(arr3)  # 输出 [1 3 ... 19]

这里跟python基础里的arange函数是一样的。

步长就相当于跳着选数据，比如说步长为3，然后有个数据是：

1 2 3 4 5 6 7 8 9 10，从1开始，那输出就是：1 4 7 10

2.3 创建同值数组

全0数组：np.zeros(shape)，输出浮点型数组。
全1数组：np.ones(shape)，输出浮点型数组。
全值数组：通过与标量相乘实现。

程序示例：

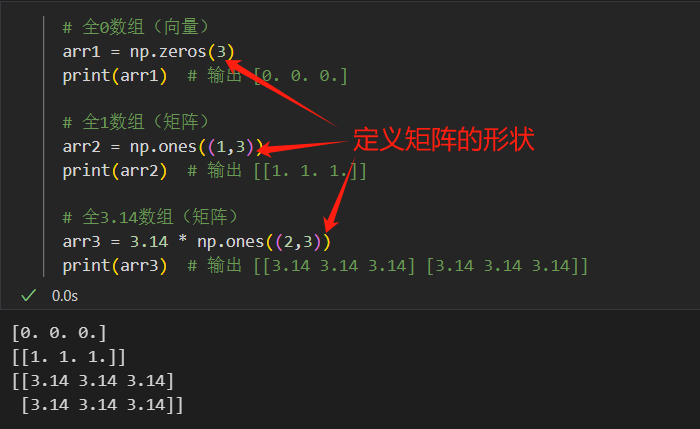
# 全0数组（向量）
arr1 = np.zeros(3)
print(arr1)  # 输出 [0. 0. 0.]# 全1数组（矩阵）
arr2 = np.ones((1,3))
print(arr2)  # 输出 [[1. 1. 1.]]# 全3.14数组（矩阵）
arr3 = 3.14 * np.ones((2,3))
print(arr3)  # 输出 [[3.14 3.14 3.14] [3.14 3.14 3.14]]

在这里插入图片描述

2.4 创建随机数组

0-1均匀分布浮点型数组：np.random.random(shape)。

arr1 = np.random.random(5)  # 形状为5的向量
print(arr1)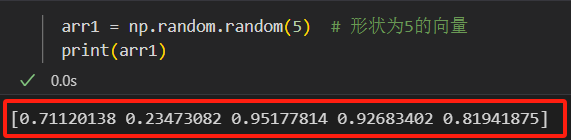

在这里插入图片描述

范围均匀分布整数数组：np.random.randint(low, high, shape)。

arr2 = np.random.randint(10,100,(1,15))  # 10-100的整数，形状(1,15)
print(arr2)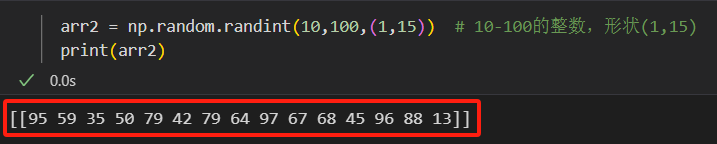

在这里插入图片描述

正态分布数组：np.random.normal(mean, std, shape)，标准正态分布可用np.random.randn(shape)。
```
arr3 = np.random.normal(0,1,(2,3))  # 均值0，标准差1，形状(2,3)
print(arr3)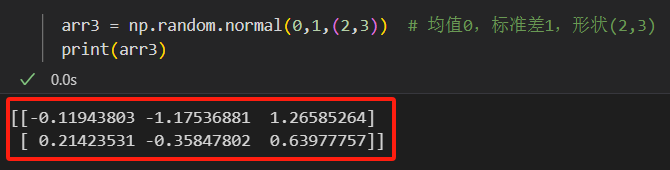  
```
范围转换：如创建60-100均匀分布3x3数组：(100-60)*np.random.random((3,3)) + 60。

这里就是说，np.random.random((3,3))生成的是形状为3*3，但是矩阵内的数值仍然是0-1之间的矩阵。

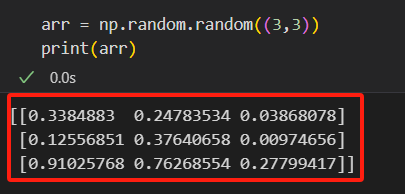
在这里插入图片描述
然后接着(100-60)*np.random.random((3,3))是因为要创建60-100，它们之间的差距为40.

此时生成的就是0-40之间的矩阵。

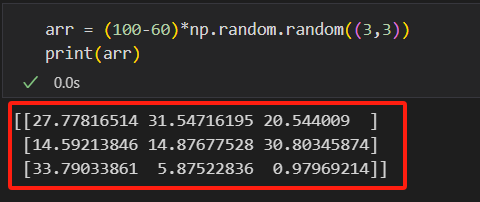
在这里插入图片描述
但我们是要求60-100，那0-40范围+60不就是60-100范围的了嘛。

3 数组的索引

在掌握了数组的创建方法后，接下来的核心问题便是如何精准地访问和修改数组中的元素，这就需要借助索引操作。

索引是数组操作中最基础也最常用的技能，无论是提取单个元素、修改特定值，还是后续更复杂的切片、筛选，都依赖于对索引规则的理解。

由于前面我们已将一维数组定义为向量、二维数组定义为矩阵，二者在结构上存在差异，因此它们的索引方式既有共通之处，也有各自的特点。

接下来，我们就具体看看如何通过索引访问向量和矩阵中的元素，以及如何通过索引修改元素的值。

3.1 访问数组元素

向量访问：与Python列表类似，索引从0开始，支持负索引。

arr1 = np.arange(1,10)  # [1 2 ... 9]
print(arr1[3])   # 访问索引3，输出4
print(arr1[-1])  # 访问最后一个元素，输出9
arr1[3] = 100    # 修改元素，数组变为 [1 2 3 100 5 ... 9]

矩阵访问：使用arr[x,y]，x为行索引，y为列索引。

arr2 = np.array([[1,2,3],[4,5,6]])
print(arr2[1,-2])  # 第1行倒数第2列，输出5
print(arr2[0,2])   # 第0行第2列，输出3
arr2[1,1] = 100.9  # 浮点数插入整数数组被截断，数组变为 [[1 2 3] [4 100 6]]

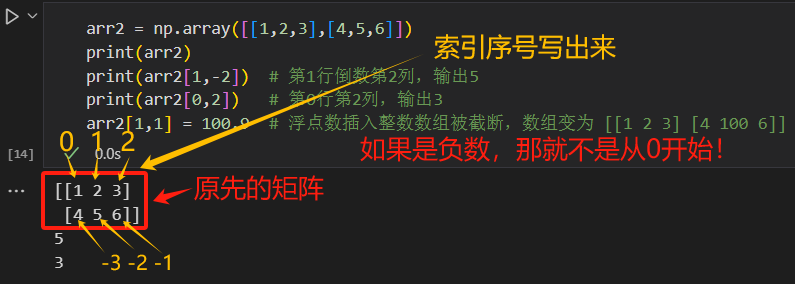
在这里插入图片描述

3.2 花式索引

定义：通过索引列表访问多个元素，向量用arr[[x1,x2...]]，矩阵用arr[[x1,x2...],[y1,y2...]]。

向量示例：

arr1 = np.arange(0,90,10)  # [0 10 20 ... 80]
print(arr1[[0,2]])  # 访问索引0和2，输出 [0 20]

矩阵示例：

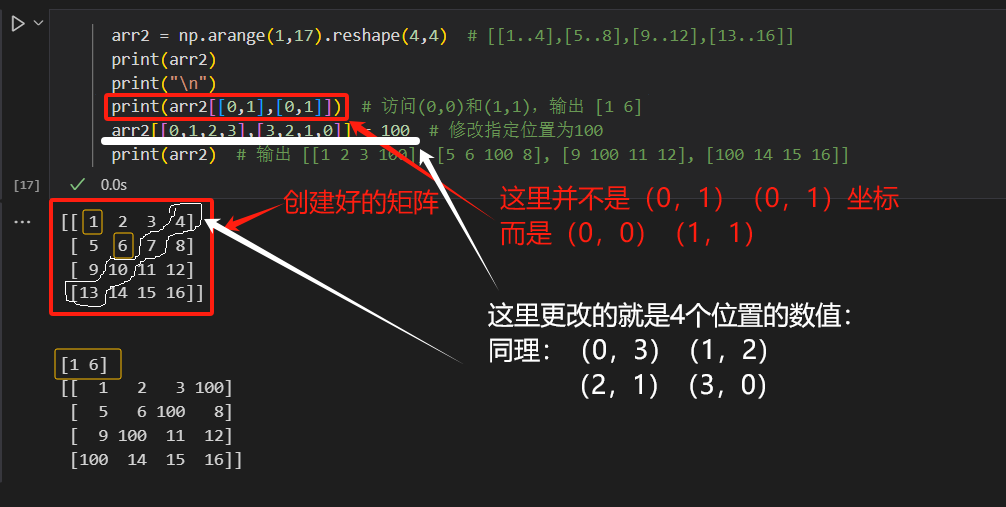
arr2 = np.arange(1,17).reshape(4,4)  # [[1..4],[5..8],[9..12],[13..16]]
print(arr2[[0,1],[0,1]])  # 访问(0,0)和(1,1)，输出 [1 6]
arr2[[0,1,2,3],[3,2,1,0]] = 100  # 修改指定位置为100
print(arr2)  # 输出 [[1 2 3 100], [5 6 100 8], [9 100 11 12], [100 14 15 16]]

在这里插入图片描述

3.3 访问数组切片

3.3.1 向量的切片

方法：与Python列表切片一致，arr[start:end:step]，默认step=1，start缺省为0，end缺省为数组长度。

程序示例：

arr1 = np.arange(10)  # [0 1 ... 9]
print(arr1[1:4])   # 从索引1到4之前，输出 [1 2 3]
print(arr1[1:])    # 从索引1到结尾，输出 [1 ... 9]
print(arr1[:4])    # 从开头到索引4之前，输出 [0 1 2 3]
print(arr1[2:-2])  # 切除开头2个和结尾2个，输出 [2 3 4 5 6 7]
print(arr1[::2])   # 每2个元素采样，输出 [0 2 4 6 8]

3.3.2 矩阵的切片

方法：arr[行切片, 列切片]，行/列切片规则同向量。

程序示例：

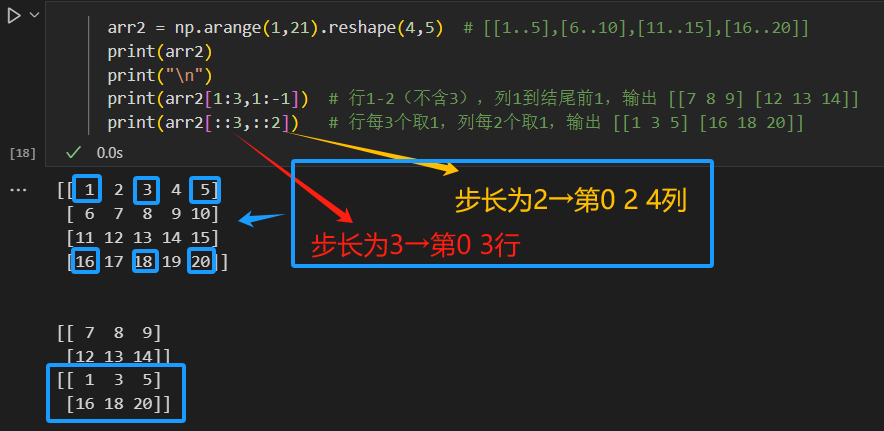
arr2 = np.arange(1,21).reshape(4,5)  # [[1..5],[6..10],[11..15],[16..20]]
print(arr2[1:3,1:-1])  # 行1-2（不含3），列1到结尾前1，输出 [[7 8 9] [12 13 14]]
print(arr2[::3,::2])   # 行每3个取1，列每2个取1，输出 [[1 3 5] [16 18 20]]

在这里插入图片描述

3.3.3 提取矩阵的行

方法：arr[行索引, :]，可简写为arr[行索引]。

程序示例：

arr3 = np.arange(1,21).reshape(4,5)
print(arr3[2,:])    # 第2行，输出 [11 12 13 14 15]
print(arr3[1:3,:])  # 行1-2，输出 [[6 7 8 9 10] [11 12 13 14 15]]
print(arr3[2])      # 简写，输出 [11 12 13 14 15]

在这里插入图片描述

3.3.4 提取矩阵的列

方法：arr[:, 列索引]，单独提取一列输出为向量，需转为列矩阵可使用reshape(-1,1)。

程序示例：

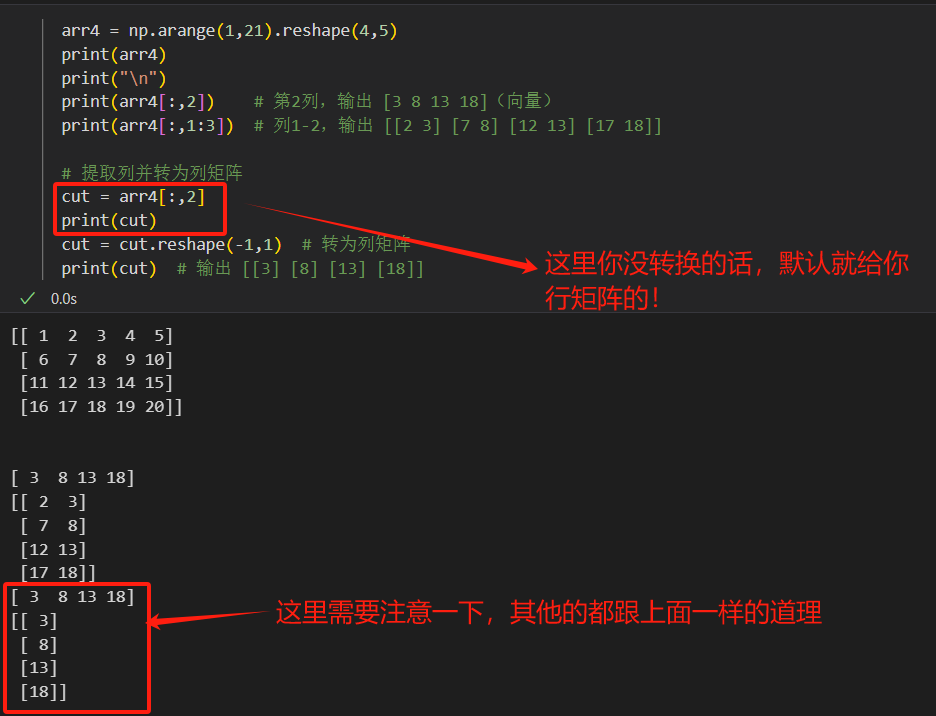
arr4 = np.arange(1,21).reshape(4,5)
print(arr4[:,2])    # 第2列，输出 [3 8 13 18]（向量）
print(arr4[:,1:3])  # 列1-2，输出 [[2 3] [7 8] [12 13] [17 18]]# 提取列并转为列矩阵
cut = arr4[:,2]
cut = cut.reshape(-1,1)  # 转为列矩阵
print(cut)  # 输出 [[3] [8] [13] [18]]

也是同样的道理。

在这里插入图片描述

3.4 数组切片仅是视图

特点：NumPy数组的切片是原数组的视图，修改切片会改变原数组，不创建新变量。

程序示例：

arr = np.arange(10)  # [0 1 ... 9]
cut = arr[:3]        # 切片 [0 1 2]
cut[0] = 100         # 修改切片
print(cut)  # 输出 [100 1 2]
print(arr)  # 原数组变为 [100 1 2 3 ... 9]

创建新变量：使用.copy()方法，修改拷贝不影响原数组。

arr = np.arange(10)
copy = arr[:3].copy()  # 拷贝切片
copy[0] = 100
print(copy)  # [100 1 2]
print(arr)   # 原数组仍为 [0 1 2 3 ... 9]

3.5 数组赋值仅是绑定

特点：数组赋值是变量绑定，两个变量指向同一数组，修改一个会影响另一个。

程序示例：

arr1 = np.arange(10)  # [0 1 ... 9]
arr2 = arr1           # 绑定
arr2[0] = 100         # 修改arr2
print(arr2)  # [100 1 ... 9]
print(arr1)  # 原数组变为 [100 1 ... 9]

复制为新变量：使用.copy()方法。

arr1 = np.arange(10)
arr2 = arr1.copy()  # 拷贝
arr2[0] = 100
print(arr2)  # [100 1 ... 9]
print(arr1)  # 原数组仍为 [0 1 ... 9]

4 数组的变形

4.1 数组的转置

方法：使用.T，仅对矩阵有效，向量需先转为矩阵。

向量转置：

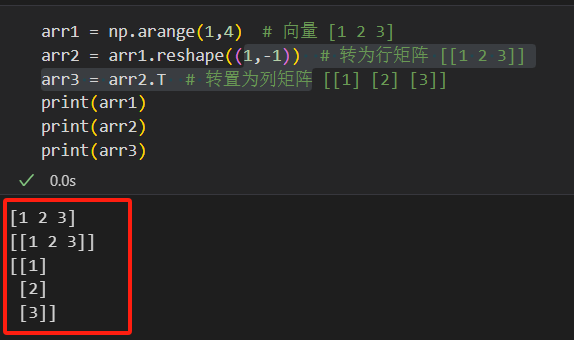
arr1 = np.arange(1,4)  # 向量 [1 2 3]
arr2 = arr1.reshape((1,-1))  # 转为行矩阵 [[1 2 3]]
arr3 = arr2.T  # 转置为列矩阵 [[1] [2] [3]]

在这里插入图片描述

矩阵转置：

# 列矩阵转置
arr1 = np.arange(3).reshape(3,1)  # 列矩阵 [[0] [1] [2]]
arr2 = arr1.T  # 转置为行矩阵 [[0 1 2]]# 普通矩阵转置
arr1 = np.arange(4).reshape(2,2)  # [[0 1] [2 3]]
arr2 = arr1.T  # 转置为 [[0 2] [1 3]]

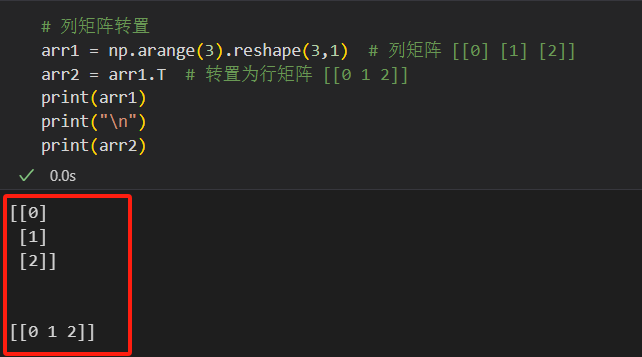
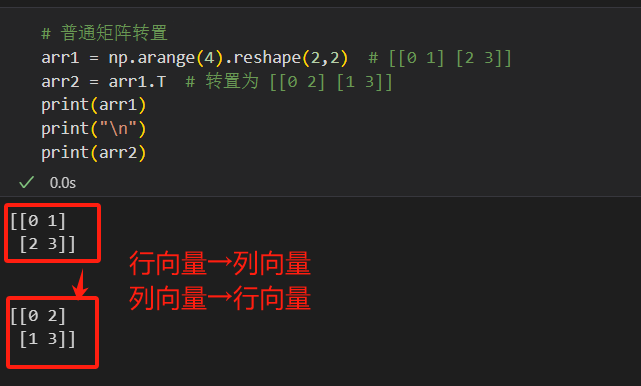
在这里插入图片描述

4.2 数组的翻转

上下翻转：np.flipud(arr)（up-down），向量只能用此方法。
左右翻转：np.fliplr(arr)（left-right），仅对矩阵有效。

程序示例：

# 向量翻转
arr1 = np.arange(10)  # [0 1 ... 9]
arr_ud = np.flipud(arr1)  # 输出 [9 8 ... 0]# 矩阵翻转
arr2 = np.arange(1,21).reshape(4,5)  # [[1..5], [6..10], [11..15], [16..20]]
arr_lr = np.fliplr(arr2)  # 左右翻转，输出 [[5..1], [10..6], [15..11], [20..16]]
arr_ud = np.flipud(arr2)  # 上下翻转，输出 [[16..20], [11..15], [6..10], [1..5]]

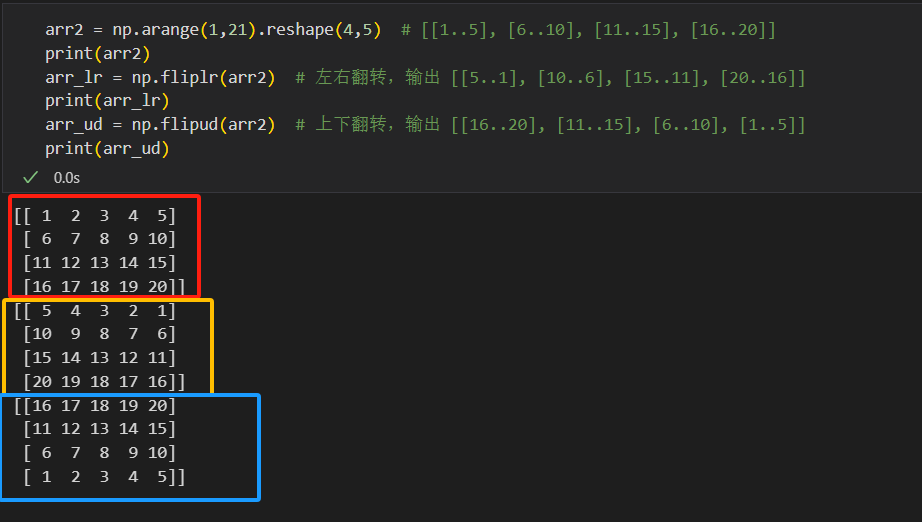
在这里插入图片描述

4.3 数组的重塑

方法：使用.reshape(shape)，-1表示自动计算维度。

向量变形：

arr1 = np.arange(1,10)  # 向量 [1 ... 9]
arr2 = arr1.reshape(3,3)  # 重塑为3x3矩阵 [[1 2 3] [4 5 6] [7 8 9]]

矩阵变形：

arr1 = np.array([[1,2,3],[4,5,6]])  # 2x3矩阵
arr2 = arr1.reshape(6)  # 重塑为向量 [1 2 3 4 5 6]
arr3 = arr1.reshape(1,6)  # 重塑为1x6矩阵 [[1 2 3 4 5 6]]

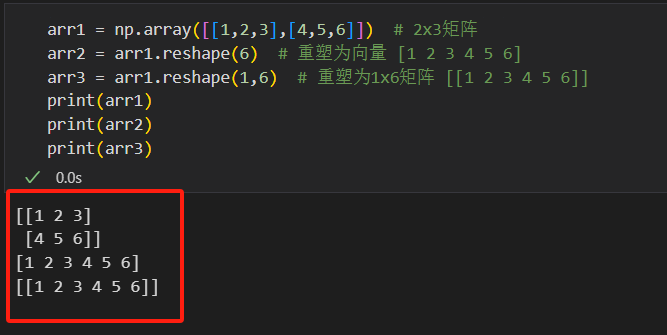
在这里插入图片描述

4.4 数组的拼接

向量拼接：np.concatenate([arr1, arr2])，结果为更长向量。

arr1 = np.array([1,2,3])
arr2 = np.array([4,5,6])
arr3 = np.concatenate([arr1, arr2])  # 输出 [1 2 3 4 5 6]

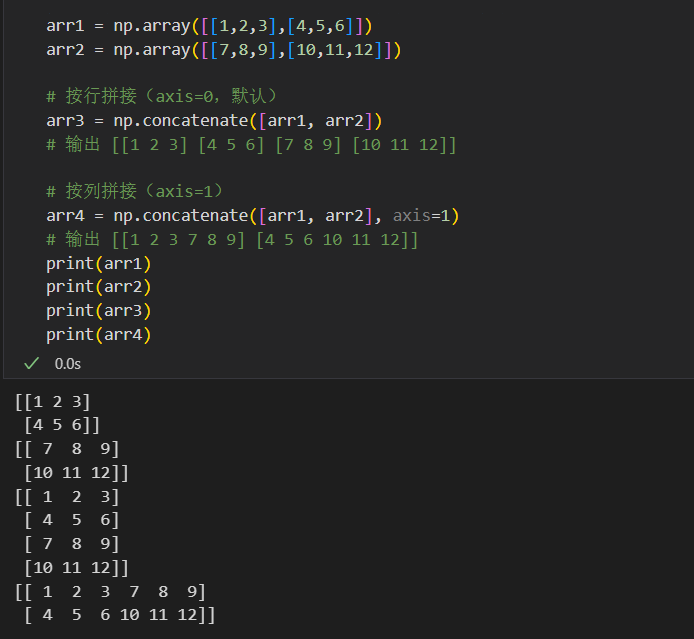
矩阵拼接：np.concatenate([arr1, arr2], axis)，axis=0按行拼接，axis=1按列拼接（需维度吻合）。

arr1 = np.array([[1,2,3],[4,5,6]])
arr2 = np.array([[7,8,9],[10,11,12]])# 按行拼接（axis=0，默认）
arr3 = np.concatenate([arr1, arr2])
# 输出 [[1 2 3] [4 5 6] [7 8 9] [10 11 12]]# 按列拼接（axis=1）
arr4 = np.concatenate([arr1, arr2], axis=1)
# 输出 [[1 2 3 7 8 9] [4 5 6 10 11 12]]

注意：向量与矩阵不可直接拼接，需先将向量升级为矩阵。

在这里插入图片描述

4.5 数组的分裂

向量分裂：np.split(arr, [索引1,索引2...])，按索引位置截断。

arr = np.arange(10,100,10)  # [10 20 ... 90]
arr1, arr2, arr3 = np.split(arr, [2,8])  # 在索引2和8截断
print(arr1)  # [10 20]
print(arr2)  # [30 40 50 60 70 80]
print(arr3)  # [90]

在这里插入图片描述

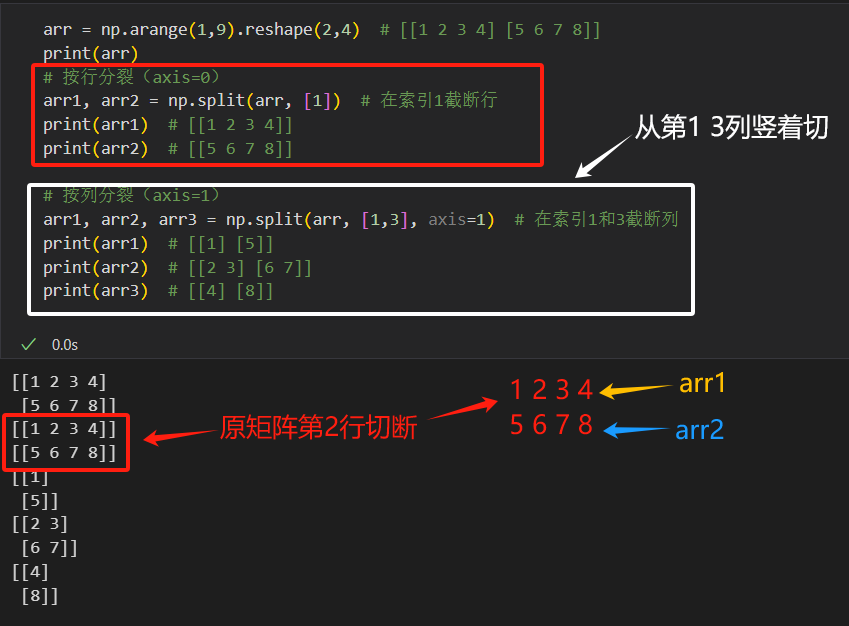
矩阵分裂：np.split(arr, [索引1...], axis)，axis=0按行分裂，axis=1按列分裂。

arr = np.arange(1,9).reshape(2,4)  # [[1 2 3 4] [5 6 7 8]]# 按行分裂（axis=0）
arr1, arr2 = np.split(arr, [1])  # 在索引1截断行
print(arr1)  # [[1 2 3 4]]
print(arr2)  # [[5 6 7 8]]# 按列分裂（axis=1）
arr1, arr2, arr3 = np.split(arr, [1,3], axis=1)  # 在索引1和3截断列
print(arr1)  # [[1] [5]]
print(arr2)  # [[2 3] [6 7]]
print(arr3)  # [[4] [8]]

在这里插入图片描述

5 数组的运算

5.1 数组与系数之间的运算

支持运算符：+、-、*、/、**、//（取整）、%（取余）。

程序示例：

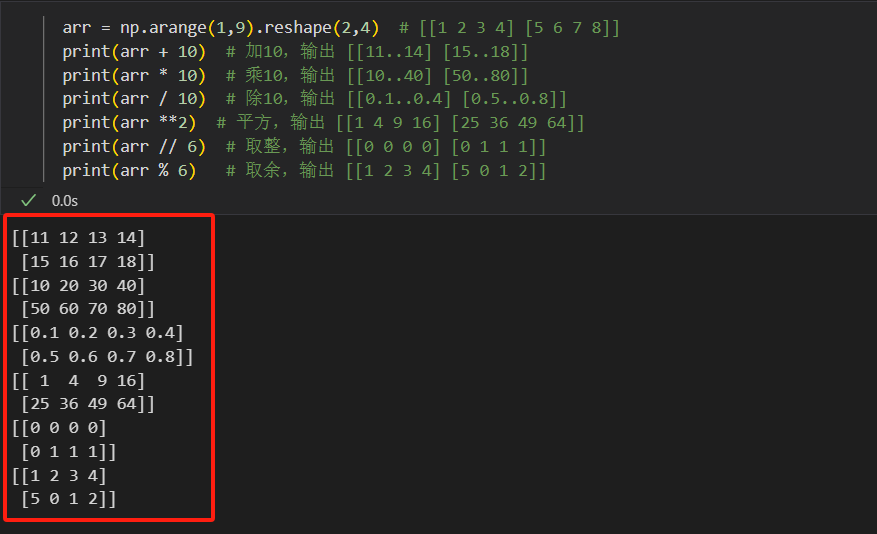
arr = np.arange(1,9).reshape(2,4)  # [[1 2 3 4] [5 6 7 8]]
print(arr + 10)  # 加10，输出 [[11..14] [15..18]]
print(arr * 10)  # 乘10，输出 [[10..40] [50..80]]
print(arr / 10)  # 除10，输出 [[0.1..0.4] [0.5..0.8]]
print(arr **2)  # 平方，输出 [[1 4 9 16] [25 36 49 64]]
print(arr // 6)  # 取整，输出 [[0 0 0 0] [0 1 1 1]]
print(arr % 6)   # 取余，输出 [[1 2 3 4] [5 0 1 2]]

在这里插入图片描述

5.2 数组与数组之间的运算

规则：同维度数组间为对应元素运算。

程序示例：

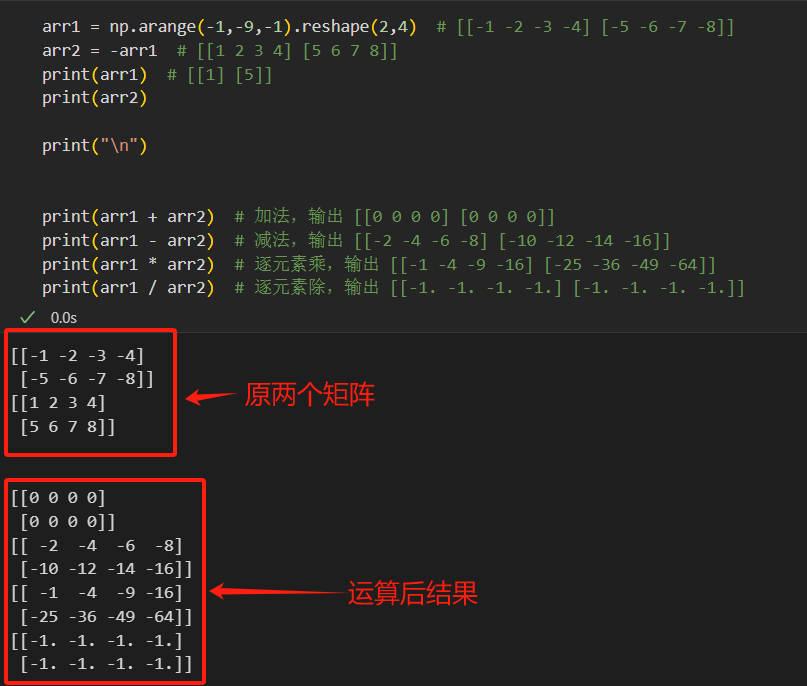
arr1 = np.arange(-1,-9,-1).reshape(2,4)  # [[-1 -2 -3 -4] [-5 -6 -7 -8]]
arr2 = -arr1  # [[1 2 3 4] [5 6 7 8]]print(arr1 + arr2)  # 加法，输出 [[0 0 0 0] [0 0 0 0]]
print(arr1 - arr2)  # 减法，输出 [[-2 -4 -6 -8] [-10 -12 -14 -16]]
print(arr1 * arr2)  # 逐元素乘，输出 [[-1 -4 -9 -16] [-25 -36 -49 -64]]
print(arr1 / arr2)  # 逐元素除，输出 [[-1. -1. -1. -1.] [-1. -1. -1. -1.]]

在这里插入图片描述

5.3 广播机制

规则：不同形状数组运算时，自动扩展以适配形状。
- 向量与矩阵：向量自动升级为行矩阵，再广播为矩阵形状（向量长度需与矩阵列数一致）。
- 行矩阵与列矩阵：分别广播为同形状矩阵。

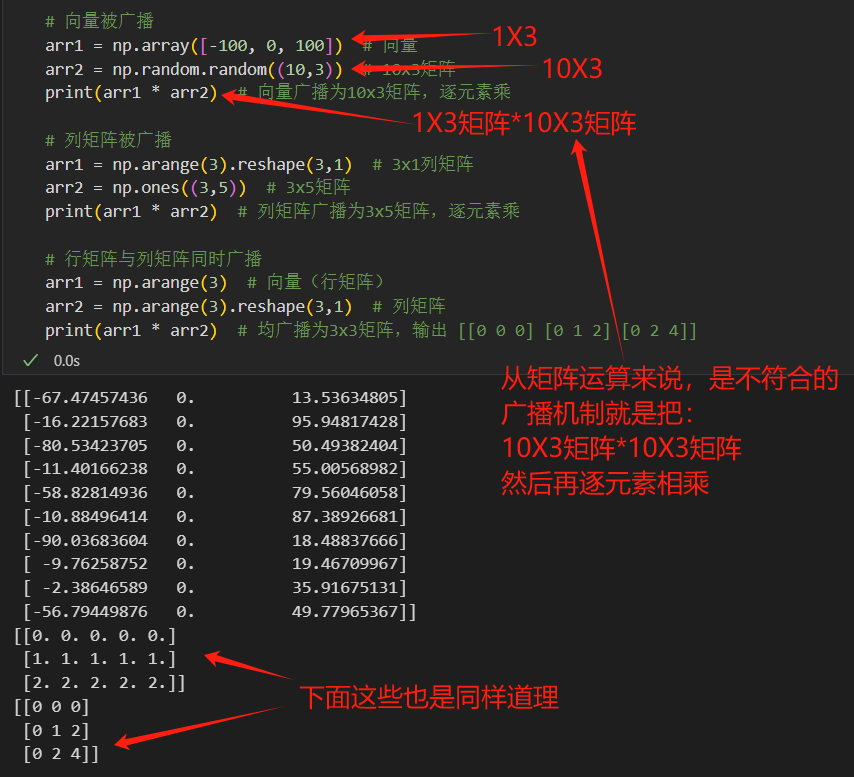
示例：

# 向量被广播
arr1 = np.array([-100, 0, 100])  # 向量
arr2 = np.random.random((10,3))  # 10x3矩阵
print(arr1 * arr2)  # 向量广播为10x3矩阵，逐元素乘# 列矩阵被广播
arr1 = np.arange(3).reshape(3,1)  # 3x1列矩阵
arr2 = np.ones((3,5))  # 3x5矩阵
print(arr1 * arr2)  # 列矩阵广播为3x5矩阵，逐元素乘# 行矩阵与列矩阵同时广播
arr1 = np.arange(3)  # 向量（行矩阵）
arr2 = np.arange(3).reshape(3,1)  # 列矩阵
print(arr1 * arr2)  # 均广播为3x3矩阵，输出 [[0 0 0] [0 1 2] [0 2 4]]

在这里插入图片描述

6 数组的函数

6.1 矩阵乘积

方法：使用np.dot(a, b)，为线性代数中的矩阵乘积。

向量与向量：

arr1 = np.arange(5)  # [0 1 2 3 4]
arr2 = np.arange(5)
print(np.dot(arr1, arr2))  # 内积，0*0+1*1+...+4*4=30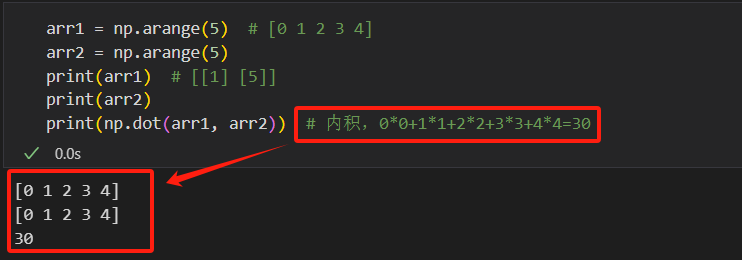

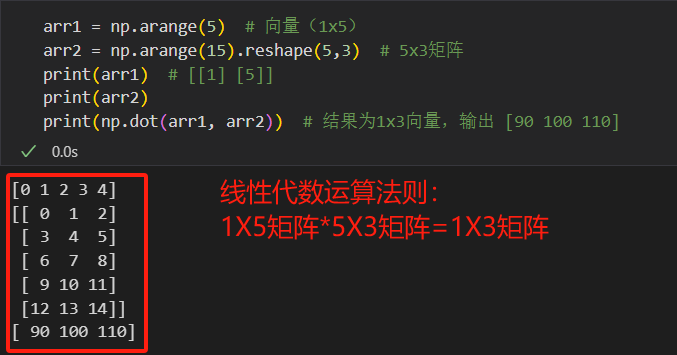
在这里插入图片描述

向量与矩阵：

arr1 = np.arange(5)  # 向量（1x5）
arr2 = np.arange(15).reshape(5,3)  # 5x3矩阵
print(np.dot(arr1, arr2))  # 结果为1x3向量，输出 [90 100 110]

在这里插入图片描述

矩阵与向量：

arr1 = np.arange(15).reshape(3,5)  # 3x5矩阵
arr2 = np.arange(5)  # 向量（5x1）
print(np.dot(arr1, arr2))  # 结果为3x1向量，输出 [30 80 130]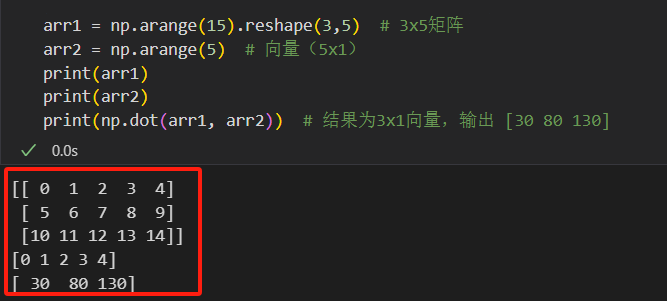

在这里插入图片描述

矩阵与矩阵：

arr1 = np.arange(10).reshape(5,2)  # 5x2矩阵
arr2 = np.arange(16).reshape(2,8)  # 2x8矩阵
print(np.dot(arr1, arr2))  # 结果为5x8矩阵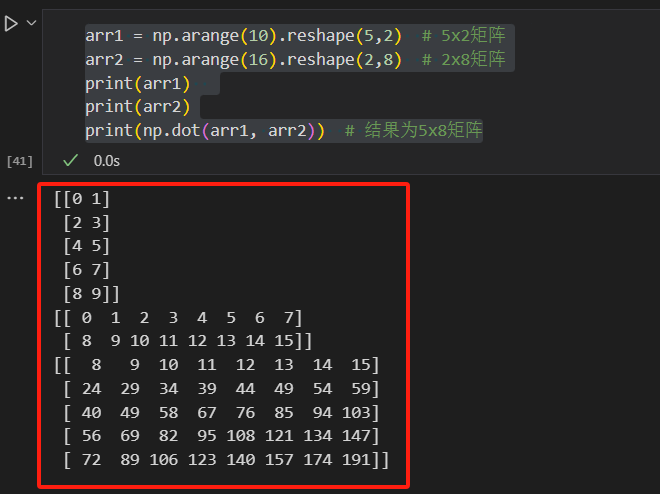

在这里插入图片描述

6.2 数学函数

绝对值：np.abs(arr)。

arr_v = np.array([-10, 0, 10])
print(np.abs(arr_v))  # 输出 [10 0 10]

三角函数：np.sin()、np.cos()、np.tan()。

theta = np.arange(3) * np.pi / 2  # [0, π/2, π]
print(np.sin(theta))  # 正弦，输出 [0.0, 1.0, 1.22e-16]

指数函数：np.exp()（e^x）、2**x、10**x。

x = np.arange(1,4)  # [1 2 3]
print(np.exp(x))  # e^x，输出 [2.718 7.389 20.086]

对数函数：np.log()（自然对数）、np.log(x)/np.log(2)（log2）、np.log(x)/np.log(10)（log10）。
```
x = np.array([1,10,100,1000])
print(np.log(x))  # 自然对数，输出 [0. 2.303 4.605 6.908]
```

6.3 聚合函数

常用函数：np.max()、np.min()、np.sum()、np.prod()、np.mean()、np.std()，支持axis参数指定维度。

示例（矩阵）：

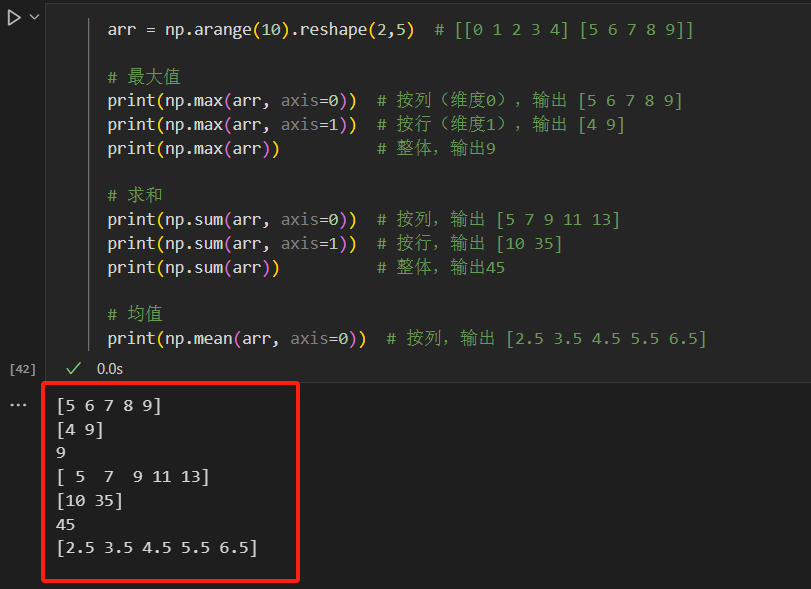
arr = np.arange(10).reshape(2,5)  # [[0 1 2 3 4] [5 6 7 8 9]]# 最大值
print(np.max(arr, axis=0))  # 按列（维度0），输出 [5 6 7 8 9]
print(np.max(arr, axis=1))  # 按行（维度1），输出 [4 9]
print(np.max(arr))          # 整体，输出9# 求和
print(np.sum(arr, axis=0))  # 按列，输出 [5 7 9 11 13]
print(np.sum(arr, axis=1))  # 按行，输出 [10 35]
print(np.sum(arr))          # 整体，输出45# 均值
print(np.mean(arr, axis=0))  # 按列，输出 [2.5 3.5 4.5 5.5 6.5]

在这里插入图片描述

7 布尔型数组

7.1 创建布尔型数组

方法：通过数组与标量/同维数组比较，或多条件组合（&与、|或、~非）。

数组与标量比较：

arr = np.arange(1,7).reshape(2,3)  # [[1 2 3] [4 5 6]]
print(arr >= 4)  # 输出 [[False False False] [True True True]]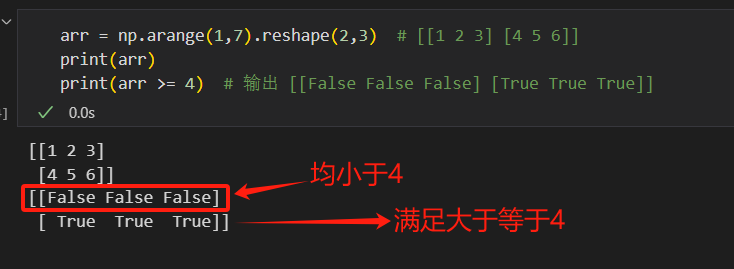

在这里插入图片描述

同维数组比较：

arr1 = np.arange(1,6)  # [1 2 3 4 5]
arr2 = np.flipud(arr1)  # [5 4 3 2 1]
print(arr1 > arr2)  # 输出 [False False False True True]

多条件组合：

arr = np.arange(1,10)  # [1..9]
print((arr < 4) | (arr > 6))  # 小于4或大于6，输出 [T T T F F F T T T]

同样的道理。

7.2 布尔型数组中True的数量

np.sum()：统计True的个数（True=1，False=0）。

arr = np.random.normal(0,1,10000)  # 10000个标准正态分布元素
num = np.sum(np.abs(arr) < 1)  # 绝对值小于1的元素个数，约6800（符合3σ准则）

np.any()：是否存在True（至少一个）。

arr1 = np.arange(1,10)
arr2 = np.flipud(arr1)
print(np.any(arr1 == arr2))  # 存在相同元素（5），输出True

np.all()：是否全为True。

arr = np.random.normal(500,70,100000)  # 模拟六级成绩
print(np.all(arr > 250))  # 是否所有成绩>250，输出False

7.3 布尔型数组作为掩码

作用：筛选普通数组中满足条件的元素，结果为向量。

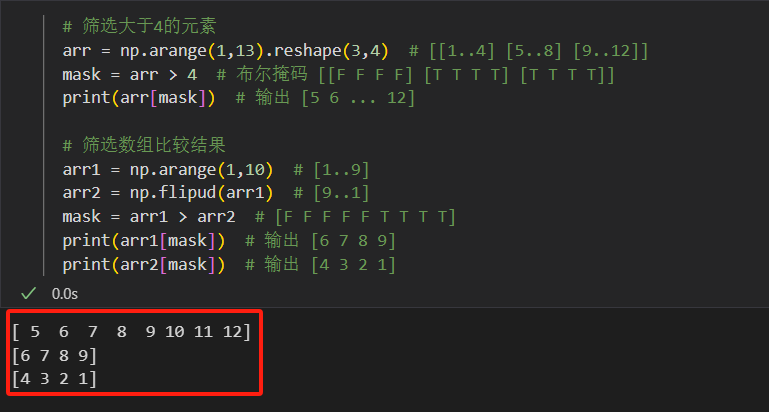
程序示例：

# 筛选大于4的元素
arr = np.arange(1,13).reshape(3,4)  # [[1..4] [5..8] [9..12]]
mask = arr > 4  # 布尔掩码 [[F F F F] [T T T T] [T T T T]]
print(arr[mask])  # 输出 [5 6 ... 12]# 筛选数组比较结果
arr1 = np.arange(1,10)  # [1..9]
arr2 = np.flipud(arr1)  # [9..1]
mask = arr1 > arr2  # [F F F F F T T T T]
print(arr1[mask])  # 输出 [6 7 8 9]
print(arr2[mask])  # 输出 [4 3 2 1]

在这里插入图片描述

7.4 满足条件的元素所在位置

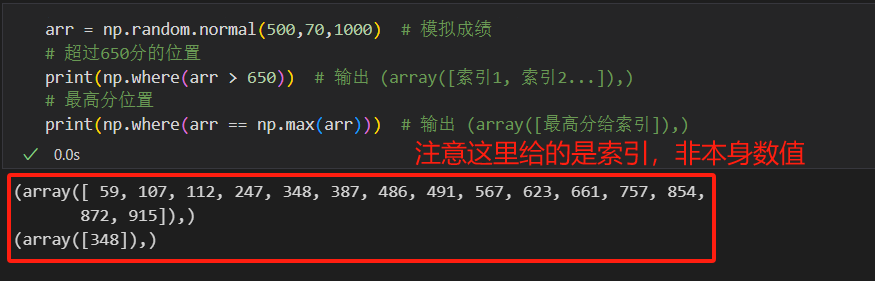
方法：使用np.where(condition)，返回满足条件元素的索引元组。

程序示例：

arr = np.random.normal(500,70,1000)  # 模拟成绩
# 超过650分的位置
print(np.where(arr > 650))  # 输出 (array([索引1, 索引2...]),)
# 最高分位置
print(np.where(arr == np.max(arr)))  # 输出 (array([最高分给索引]),)

在这里插入图片描述

8 从数组到张量

8.1 数组与张量

关系：NumPy的n维数组对应PyTorch的n阶张量，PyTorch吸收NumPy语法，运算从CPU升级到GPU。
转换：
- 数组转张量：ts = torch.tensor(arr)
- 张量转数组：arr = np.array(ts)

8.2 语法不同点

NumPy函数	PyTorch函数	用法区别
`.astype()`	`.type()`	无
`np.random.random()`	`torch.rand()`	无
`np.random.randint()`	`torch.randint()`	不接纳一维张量
`np.random.normal()`	`torch.normal()`	不接纳一维张量
`np.random.randn()`	`torch.randn()`	无
`.copy()`	`.clone()`	无
`np.concatenate()`	`torch.cat()`	无
`np.split()`	`torch.split()`	参数含义优化
`np.dot()`	`torch.matmul()`	无
`np.dot(v,v)`	`torch.dot()`	无
`np.dot(m,v)`	`torch.mv()`	无
`np.dot(m,m)`	`torch.mm()`	无
`np.exp()`	`torch.exp()`	必须传入张量
`np.log()`	`torch.log()`	必须传入张量
`np.mean()`	`torch.mean()`	必须传入浮点型张量
`np.std()`	`torch.std()`	必须传入浮点型张量

9 小结

本文系统介绍了NumPy数组库的核心知识，从数组基础到创建方法，再到索引、变形、运算、函数及布尔型数组的应用，最后衔接至张量。NumPy通过数组提供高效的数值计算能力，其切片视图、广播机制等设计优化了内存与运算效率。理解NumPy与张量的语法差异可平滑过渡到深度学习框架的使用。