一、NodePort存在的不足
1. 四层负载均衡
- 实现技术: 基于iptables和ipvs实现
- OSI层级: 位于传输层(第四层)
- 转发依据: 基于IP地址和端口进行转发
- 特点:
- 只能看到IP和端口信息
- 无法识别应用层协议内容
- 配置简单但功能有限
2. 七层负载均衡
1)七层负载均衡的概念
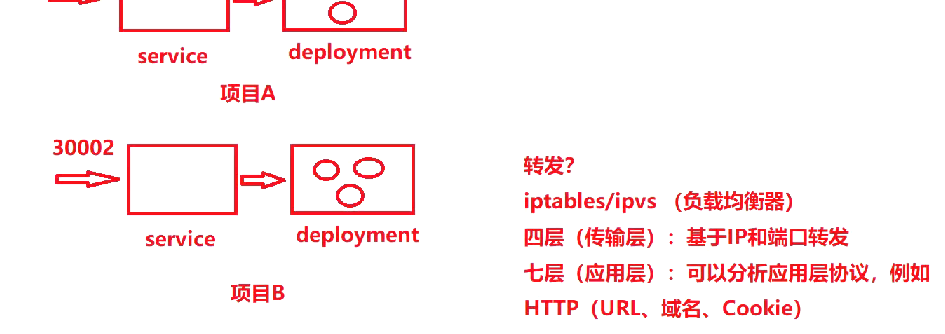
- OSI层级: 位于应用层(第七层)
- 协议分析: 可以解析应用层协议内容
- 转发依据:
- HTTP协议中的URL路径
- 域名信息
- Cookie内容
2)七层负载均衡与四层负载均衡的区别
- 功能差异:
- 七层可以实现基于域名的分流、URL重定向等高级功能
- 四层只能基于IP和端口进行简单转发
- 配置复杂度:
- 七层配置更复杂但功能强大

)




中的高电平与低电平?)

)

![[电网备考]计算机组成与原理](http://pic.xiahunao.cn/[电网备考]计算机组成与原理)




 与 HTTP API:大模型时代的通信新范式)



![0-1BFS(双端队列,洛谷P4667 [BalticOI 2011] Switch the Lamp On 电路维修 (Day1)题解)](http://pic.xiahunao.cn/0-1BFS(双端队列,洛谷P4667 [BalticOI 2011] Switch the Lamp On 电路维修 (Day1)题解))