五二维绘图

1 举例

% 二维平面绘图（扩展至 -2π 到 2π）
x = -2*pi:0.01:2*pi;  % x范围扩展为[-2π, 2π]% 绘制基础正弦函数
y = sin(x);figure % 建立画布
plot(x, y, 'b', 'LineWidth', 1.5)  % 蓝色实线，线宽1.5
title('y = sin(x)')
xlabel('x ')
ylabel('sin(x)')
% 如果不写这一行的话，在两侧留空白（如显示 [-1, 7] 而非 [0, 6.28]），而写了范围后就是[-1,7]
xlim([-2*pi 2*pi])  % 设置x轴范围（将x显示范围限制在这个区间）
grid on  % 添加网格线

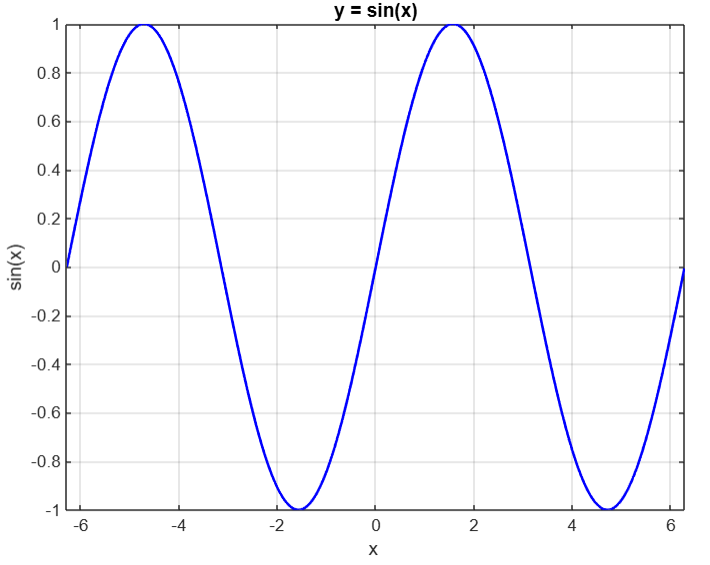
3D sin 图像郑龙浩

2 各种参数设置

① 颜色

颜色	字符	颜色	字符
红	r	粉红	m
绿	g	青	c
蓝	b	白	w
黄	y	黑	k

② 线型

线型	符号	正确示例	MATLAB显示效果
实线	`-`	`————————————————`	连续无间隔的直线
虚线	`--`	`—— —— —— —— ——`	中等长度线段+中等间隔
冒号线	`:`	`··············`	紧密排列的小点
点画线	`-.`	`—·—·—·—·—·—·—·—·`	交替的长线段和圆点

③ 标记点类型

符号	点类型	示例	符号	点类型	示例
·	点	`····`	^	上三角	`△△△△`
+	十字号	`++++`	v	下三角	`▽▽▽▽`
o	圆圈	`○○○○`	<	左三角	`◁◁◁◁`
*	星号	`****`	>	右三角	`▷▷▷▷`
x	叉号	`××××`	p	五角星	`☆☆☆☆`
s	正方形	`□□□□`	h	六角星	`⬡⬡⬡⬡`
d	菱形	`◇◇◇◇`

3 双y轴绘图 `yyaxis`

yyaxis 的核心是左右Y轴切换其余操作与普通 plot 一致。

任务：

绘制双Y轴图形，左侧为 y1 = 0.5*exp(-x)（绿色实线），右侧为 y2 = 100*log(x+1)（黑色点线），并添加网格和图例。

人话就是：左侧Y轴是绿色实线的指数函数图像的，右侧Y轴是黑色电线的对数图像的

x = 0:0.1:5;
y1 = exp(-x);
y2 = log(x+1);figure;
yyaxis left;
plot(x, y1, 'g-', 'LineWidth', 1.5);
ylabel('exp(-x)'); % 左侧Y轴的名字yyaxis right;
plot(x, y2, 'k:', 'LineWidth', 2);
ylabel('ln(x+1)'); % 右侧Y轴的名字

图像：

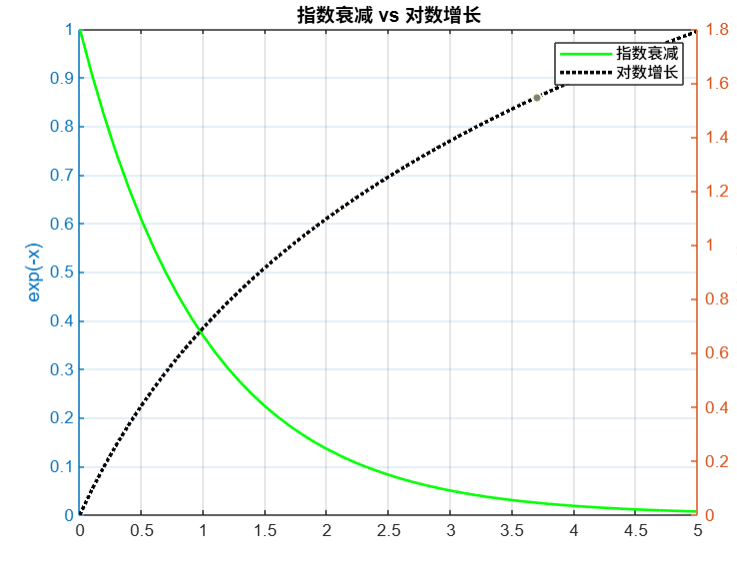
3D 指数函数+对数函数郑龙浩

六三维绘图

1 基本介绍

绘制二维图用的是plot()，绘制三维图用的是plot3

plot3(X, Y, Z, '参数')

属性的话，可以写到一起，不是必须得分开的

plot3(x, y, z, 'r--0') % 意思就是红色虚线原点标记三维图像

当然，生成三维图像不是只可以从一个角度看，可以进行旋转，从多个角度去观看

2 用view()去调整

1）简单介绍

当然也可以用view(n,m)去观察角度

n 表示的是方位角

m 表示的是仰角

角度都是°

2）用`view(30, 30)`举例来说明：

第一个 30：方位角

定义：观察者绕 Z 轴（垂直屏幕的轴）逆时针旋转的角度
- 0°：正对 X 轴正方向（从正前方看）
- 90°：正对 Y 轴正方向（从右侧看）
- 30°：介于正前方和右侧之间的斜视角。
类比：像人站在物体周围 水平移动（左右转头）

2. 第二个 30：仰角

定义：观察者相对于 XY 平面（水平面）的俯仰角度。
- 0°：平视（视线与 XY 平面平行）。
- 90°：正上方俯视（鸟瞰图）。
- 30°：轻微俯视（视线从斜上方看向物体）。
类比：像人 抬头或低头 看物体。

3. view(30, 30) 的视觉效果

方位角 30°：视角从正前方偏右 30° 方向观察。
仰角 30°：视线从斜上方 30° 向下看。

常用视角如下

代码	视角描述	适用场景
`view(0, 90)`	正上方俯视（只看 XY 平面）	二维数据的热力图
`view(0, 0)`	平视（沿 X 轴）	侧视轮廓分析
`view(30, 30)`	斜向上 30° 看	展示三维立体效果（默认）
`view(-37.5, 30)`	MATLAB 默认三维视角	通用三维图形

3 举例

① 三维直线

红色+圆圈+实线

X = [1, 2];  % X坐标
Y = [1, 3];  % Y坐标
Z = [1, 4];  % Z坐标plot3(X, Y, Z, 'ro-', 'LineWidth', 2);  % 红色圆圈标记+实线
xlabel('X'); 
ylabel('Y'); 
zlabel('Z');
title('3D 直线');
grid on;

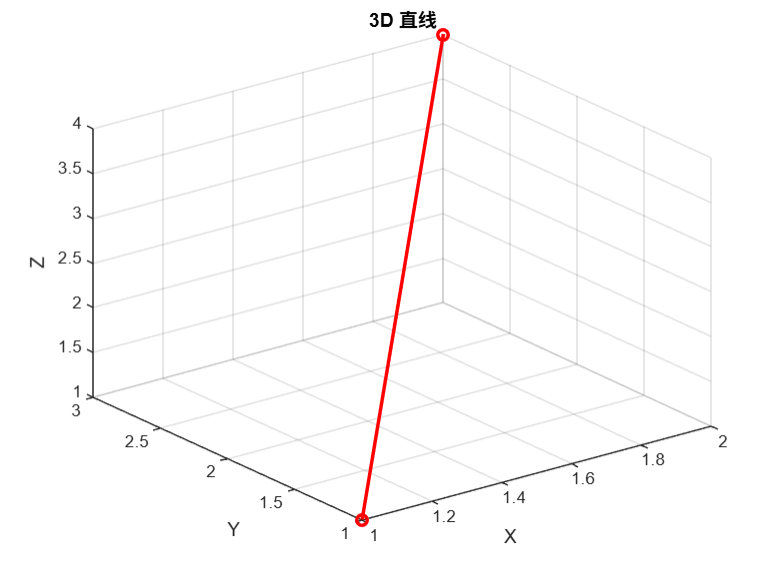
3D 直线郑龙浩1
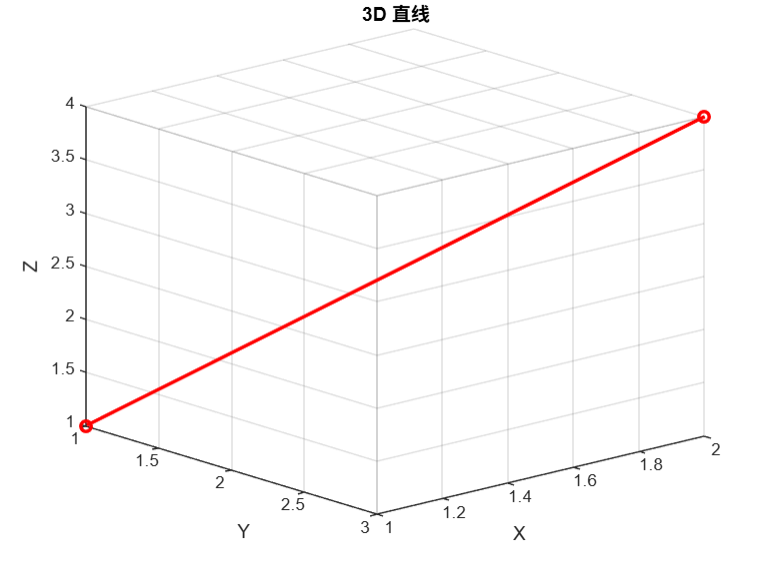
3D 直线郑龙浩2

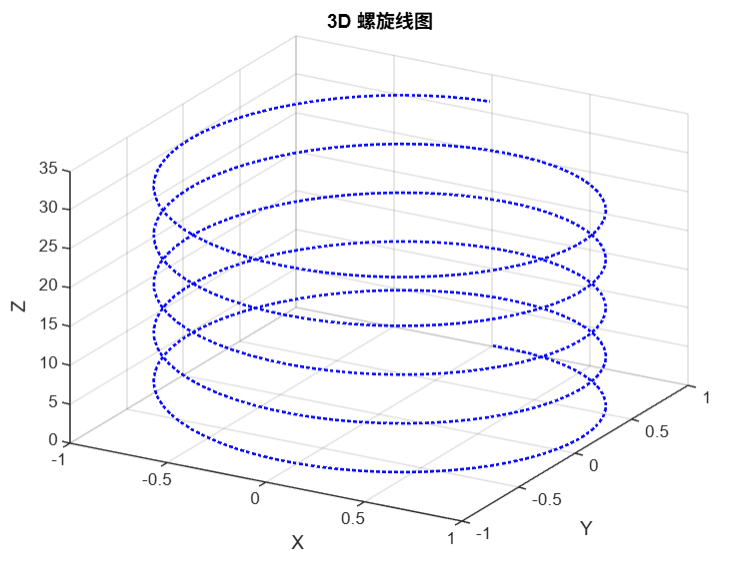
② 3D 螺旋线图

t = 0:0.1:10*pi;  % 参数 t
x = sin(t);
y = cos(t);
z = t;plot3(x, y, z, 'b:', 'LineWidth', 1.5);
xlabel('X'); 
ylabel('Y'); 
zlabel('Z');
title('3D 螺旋线图');
grid on;
view(30, 30);  % 调整视角

3D 螺旋线郑龙浩

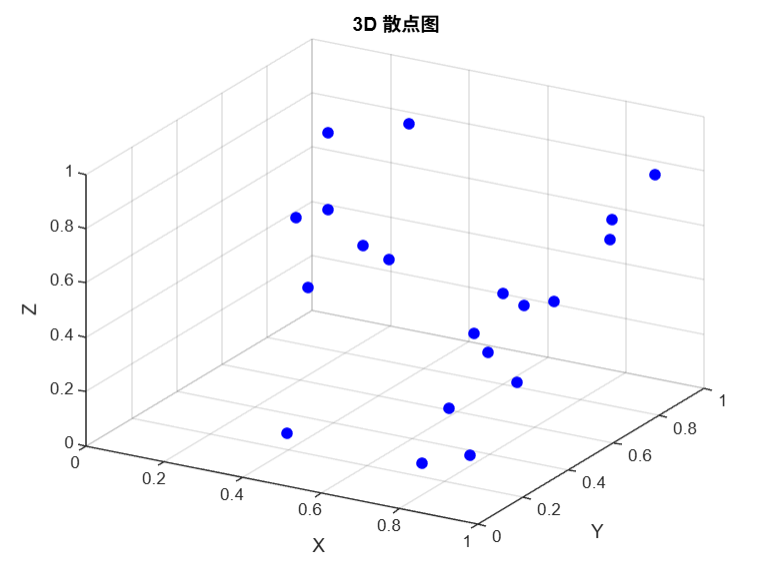
③ 3D 散点图

rng(0);  % 固定随机数种子
X = rand(20, 1);  % 20个随机X坐标
Y = rand(20, 1);  % 20个随机Y坐标
Z = rand(20, 1);  % 20个随机Z坐标plot3(X, Y, Z, 'b.', 'MarkerSize', 20);
xlabel('X'); ylabel('Y'); zlabel('Z');
title('3D 散点图');
grid on;
view(30, 30)