在这里插入图片描述

博主简介：努力学习的22级计算机科学与技术本科生一枚🌸
博主主页： @Yaoyao2024
往期回顾：【二分图算法】手把手教你学会：染色法（判断二分图）、匈牙利算法（二分图的最大匹配）
每日一言🌼: 莫等闲、白了少年头，空悲切！——岳飞《满江红·怒发冲冠》🌺

前言

组合优化是运筹学中的核心领域，专注于在离散对象的有限集合中寻找“最佳”组合方式。这类问题普遍存在于现实世界，从物流路径规划到金融资产配置，再到算法设计，其核心挑战是如何在“组合爆炸”的庞杂解空间中高效锁定最优解。

一、组合优化是什么？

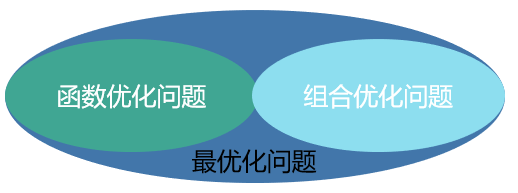
组合优化研究的是 “离散对象的选取、排列或分配” 问题，其目标是从有限个可行解中找出一个最优解。它和连续优化（如求函数极值）的根本区别在于解空间的离散性——解是整数、集合、排列或图结构，而非连续实数。
在这里插入图片描述
组合优化是运筹学中的核心领域，专注于在离散对象的有限集合中寻找“最佳”组合方式。这类问题普遍存在于现实世界，从物流路径规划到金融资产配置，再到算法设计，其核心挑战是如何在“组合爆炸”的庞杂解空间中高效锁定最优解。以下将从概念、起源、经典问题及求解逻辑四个维度展开系统解析，力求清晰易懂。

关键特征包括：

解空间离散且有限（如路径排列、资产组合选择）；
目标函数明确 最优化问题（最小化成本或最大化收益）；
约束条件强（如每个城市仅访问一次、投资权重和为1）；
NP困难性：多数经典问题随着规模扩大，计算复杂度呈指数级增长，无法在多项式时间内精确求解。

例如在旅行商问题（TSP）中：

目标：找到访问所有城市一次并返回起点的最短路径；
约束：每个城市仅访问一次；
复杂度：城市数n=20时，路径数约为 $19!=19×18×...×1=121,645,100,408,832,000≈1.2×101719!=19\times18\times...\times1=121,645,100,408,832,000\approx1.2\times10^{17}$ ，即使每秒计算100万次，也需1929年才能穷举完。

二、起源：从数学游戏到现代算法基石

组合优化虽在20世纪中期形成体系，但思想源头可追溯至18世纪：

1736年：哥尼斯堡七桥问题
18世纪时，俄罗斯的哥尼斯堡市（现加里宁格勒）有7座桥连接河的两岸和河中的两个岛（如下图）。当时市民们都在讨论：

“能不能设计一条散步路线，恰好每座桥只走一次，最后回到起点？”

欧拉（著名数学家）在1736年证明：不可能做到。这个研究成了图论的起点。

欧拉的规则：
要"一笔画"走完所有桥（不重复、不遗漏），必须满足：

除了起点和终点，其他点连接的桥数必须是偶数（进去和出来的次数相等）。
如果起点≠终点，则这两个点连接的桥数可以是奇数。

检查哥尼斯堡七桥：

A连接3座桥（奇数 ❌）
B连接3座桥（奇数 ❌）
C连接5座桥（奇数 ❌）
D连接3座桥（奇数 ❌）
→ 全都不满足，所以无解！
1950–60s：算法理论大爆发
- 1952年：Dijkstra 最短路径算法
  解决图中两点间最短路径，其核心是“贪心标记法”：通过逐步移动标签、更新距离估值，避开无效路径搜索。
- 1952年：Markowitz 投资组合理论
  提出用均值衡量收益、方差衡量风险，首次将资产配置转化为数学优化问题，奠定金融工程基础。
- 1962年：Gale-Shapley 稳定匹配算法
  解决“稳定婚姻问题”，应用于医学生住院匹配、器官捐献系统，2012年获诺贝尔经济学奖。
1964年：计算复杂性理论建立
Cook 提出 P/NP 问题分类，组合优化中的 TSP、背包问题等被证明属于 NP-Hard 类——除非 P=NP，否则不存在高效精确解法。

三、经典问题：理解组合优化的“代表难题”

以下是几类经典问题，它们结构简单却极具代表性，共同点是描述容易、求解极难：

问题类型	描述	应用场景
旅行商问题（TSP）	找访问所有城市的最短环路	物流配送、电路板钻孔路径规划
0-1背包问题	在容量限制下选择物品使总价值最大	资源分配、投资组合筛选
图着色问题	用最少颜色为图顶点着色，使相邻点颜色不同	课程排表、频谱分配
作业车间调度	安排工件在多台机器上的加工顺序，使总完成时间最短	制造业生产优化
稳定匹配	根据偏好匹配两组对象（如医生与医院），使不存在更优的“私下交换”组合	择校系统、实习匹配

为什么这些问题难？
以 TSP 为例：城市数 n 增加时，路径数按阶乘增长（n!）。n=30 时，路径比宇宙原子数还多。

四、求解逻辑：从暴力穷举到智能优化

针对“组合爆炸”挑战，学界发展出多层解法体系，核心思想是用策略换效率：

1. 精确算法：求最优解，但仅适用小规模

分支定界法：通过“分而治之+剪枝”缩小搜索空间
例：求解TSP时，提前剪掉成本超界的路径分支。
动态规划：存储子问题解，避免重复计算
例：背包问题中递归定义最优子结构。

2. 近似算法：用可接受误差换时间效率

保证解在多项式时间内达到最优解的 (1+ε) 倍内
例：Christofides 算法求TSP，解不超过最优的1.5倍。

3. 启发式算法：经验规则指导搜索

贪婪算法：每一步选当前最优
例：Dijkstra算法本质是贪心策略。
局部搜索：迭代改进当前解（如2-opt交换TSP路径）。

4. 元启发式算法：通用优化框架

方法	原理	优势
模拟退火	模拟金属冷却过程，以概率接受“暂时变差解”避免陷入局部最优	通用性强，适合复杂地形优化
遗传算法	模拟自然选择，通过交叉、变异生成新解	并行性好，适合多峰值问题
蚁群优化	模拟蚂蚁信息素机制，正反馈引导搜索方向	在路径类问题中表现优异