前言

没做出来，看了很多篇题解后AC了，感觉大部分题解讲得不清楚。

题目

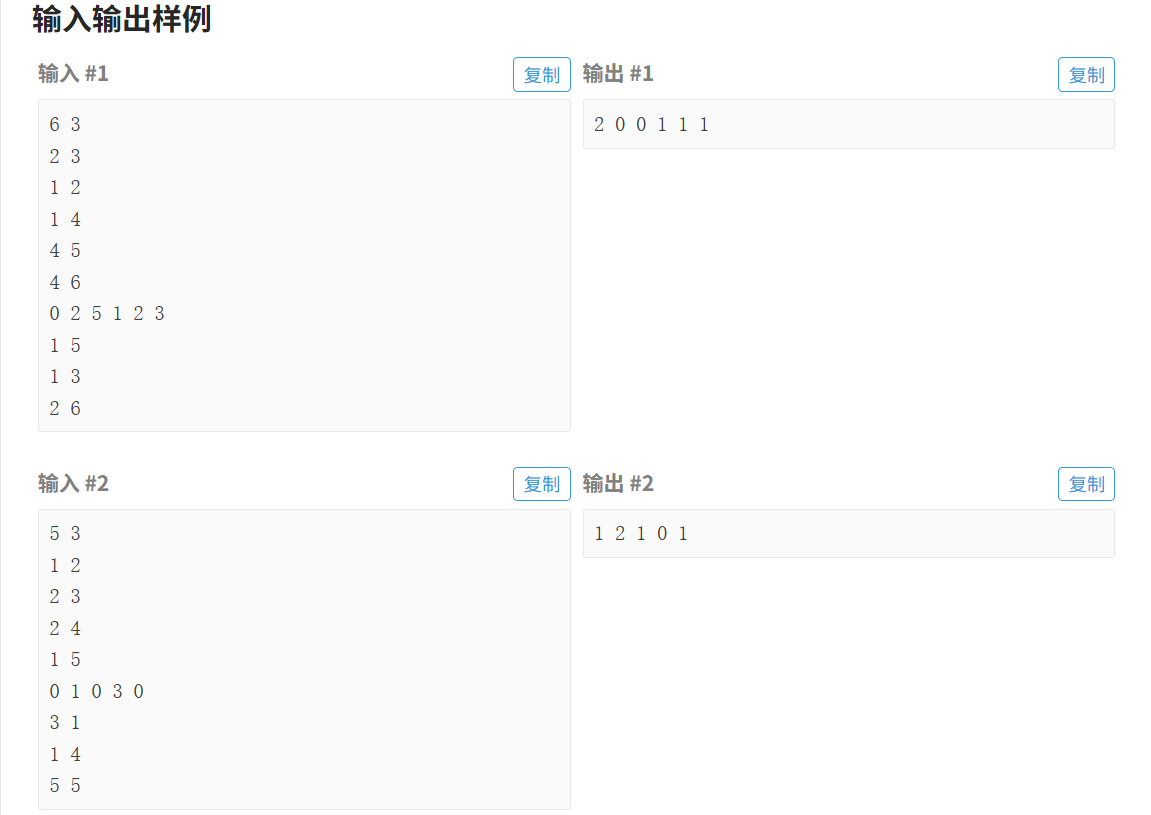
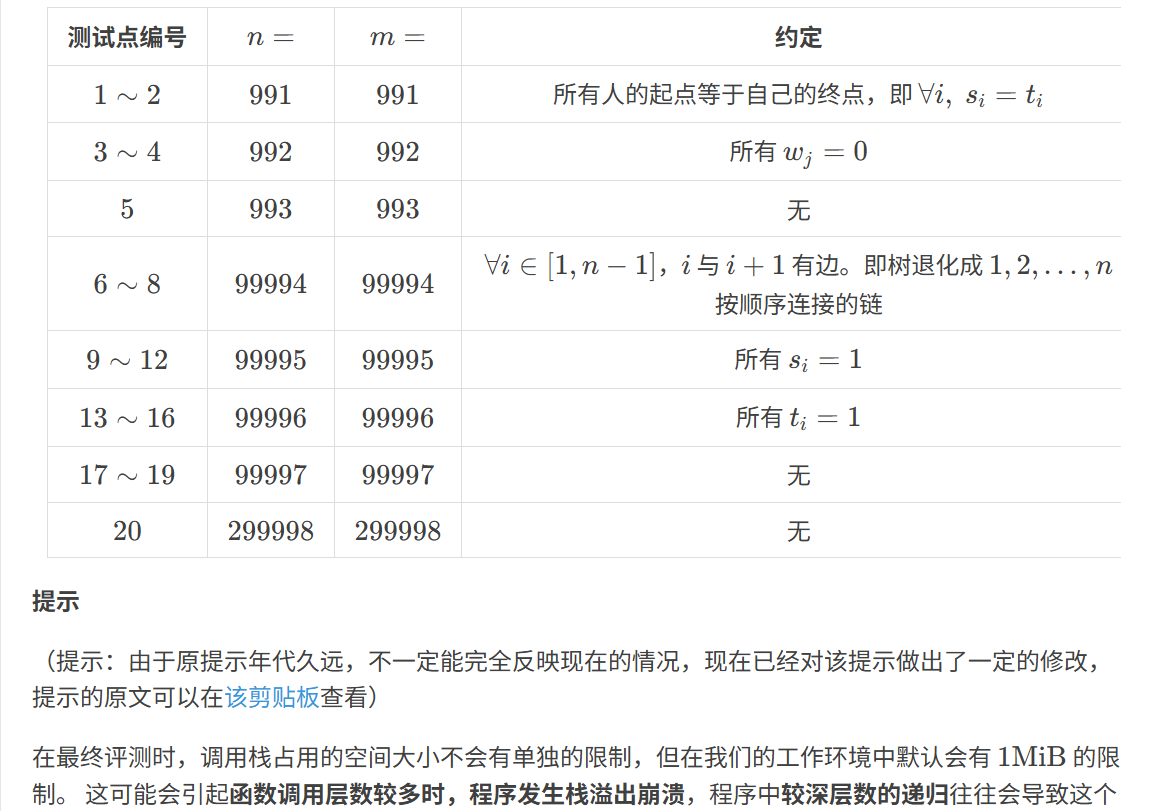
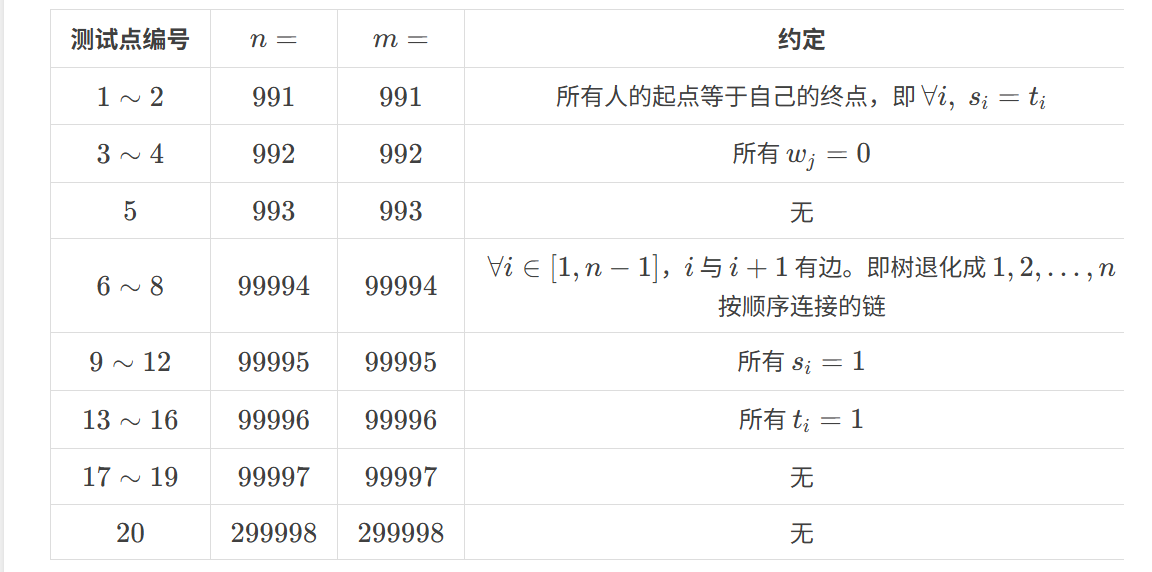
思路

结果有两种求法

模拟跑步过程，统计每个节点能观察到的人数
考虑每条路径会对哪些节点作出贡献（当前路径的玩家能被观察到）

尝试

第一种求法必须遍历当前路径的所有节点，不能优化，因为不能跳过任何节点，最坏时间复杂度O(nm)，超时，换思路。

正解思路

不再遍历统计，换第二种求法。

路径 si → ti 若能对节点 u 有贡献，节点u一定是路径L上的节点。

分情况讨论

节点u在路径 si → lca(si, ti) 上，设depth[i] = 节点i的深度（根节点为1），此时depth[si] = depth[u] + w[u]。
节点u在路径 lca(si, ti) → ti 上，设dis(x, y) = x到y之间的距离，此时 dis(si, ti) = w[u] + (depth[ti] - depth[u])，移项得 dis(si, ti) - depth[ti] = w[u] - depth[u]，移项后等式左边是已知量。

根据等式，且n < 10^6，用桶快速得出节点观察到的人数，设 cntStart[depth[u] + w[u]] = 满足节点 u 的 si（即depth[si] = depth[u] + w[u]），起点为 si 的路径个数；cntLast[w[u] - depth[u]] = 满足节点 u 的 ti，（即dis(si, ti) - depth[ti] = w[u] - depth[u]），终点为ti的路径个数。

设result[u] = 在节点u能观察到的人数（相当于路径数）。

除了节点 u = lca(si, ti) 的情况，节点u要么在路径 si → lca(si, ti) 上，此时 result[u] += 起点为 si 的路径个数，要么在路径 lca(si, ti) → ti 上，此时 result[u] += 终点为ti的路径个数，路径个数正确统计。

当节点 u = lca(si, ti)，若 si 和 ti 会对节点u产生贡献，此时 result[u] += 起点为 si 的路径个数 + 终点为ti的路径个数，si → ti 的路径会被计算两次（si 计算一次，ti 计算一次），需要result[u] = result[u] - 1。

当路径 si → ti 的 si 满足 depth[si] = depth[lca(si, ti)] + w[lca(si, ti)]，ti也会满足dis(si, ti) - depth[ti] = w[lca(si, ti)] - depth[lca(si, ti)]。

证明

depth[lca(si, ti)] + w[lca(si, ti)] = w[lca(si, ti)] - depth[lca(si, ti)] + 2 × depth[lca(si, ti)]，

那么有

dis(si, ti) - depth[ti] + 2 × depth[lca(si, ti)] = w[lca(si, ti)] - depth[lca(si, ti)] + 2 × depth[lca(si, ti)]，化简得

depth[si] = depth[lca(si, ti)] + w[lca(si, ti)] 。

证毕

所以只要判断到 depth[si] = depth[lca(si, ti)] + w[lca(si, ti)] ，就result[lca(si, ti)] = result[lca(si, ti)] - 1。

实现

发现无论什么情况，si、ti 都在以节点u为根的子树上，所以 dfs 遍历，回溯的时候统计。

tot1 = 以节点u为根的子树之外的起点 si 满足 depth[si] = depth[u] + w[u] 的路径个数，tot2 = 以节点u为根的子树之外的终点 ti 满足 dis(si, ti) - depth[ti] = w[u] - depth[u] 的路径个数，计算tot1，tot2是为了去掉节点u不再上面的路径数。根据 tot1 和 tot2 的定义，要在下一层递归前求解。

先统计节点u为起点和为终点时有贡献的路径数，可能满足 depth[si] = depth[u] + w[u] 的 si 为 u，满足 dis(si, ti) - depth[ti] = w[u] - depth[u] 的 ti 为 u。

最后减去 lca(si, ti) = u 的路径数，这些路径之后不会再被计入。

LCA用倍增加速求解。

细节见代码。

代码

#include <iostream>
#include <vector>
#include <cmath>
using namespace std;typedef long long LL;const LL Maxn = 299998 + 5;
const LL Maxm = 299998 + 5;
const LL Maxk = 20;
const LL Size = 300000;struct node {LL s, t, e;
} pla[Maxm];vector<LL> tree[Maxn];
vector<LL> tId[Maxn];
vector<LL> LId[Maxn];
LL vct_w[Maxn], depth[Maxn], father[Maxn][Maxk];
LL cnt_s[Maxn], cntStart[Maxn * 2], cntLast[Maxn * 2], result[Maxn];void init(LL u, LL fa) {depth[u] = depth[fa] + 1;father[u][0] = fa;for (LL i = 1; depth[u] > (1 << i); ++i) {father[u][i] = father[father[u][i - 1]][i - 1];}for (auto v : tree[u]) {if (v != fa)  init(v, u);}return;
}LL LCA(LL u, LL v) {if (depth[u] < depth[v])  swap(u, v);for (LL i = Maxk - 1; i >= 0; --i) {if (depth[father[u][i]] >= depth[v])  u = father[u][i];}if (u == v)  return u;for (LL i = Maxk - 1; i >= 0; --i) {if (father[u][i] != father[v][i]) {u = father[u][i];v = father[v][i];}}return father[u][0];
}void dfs(LL u, LL fa) {LL tot1 = cntStart[depth[u] + vct_w[u]], tot2 = cntLast[vct_w[u] - depth[u] + Size];for (auto v : tree[u]) {if (v != fa)  dfs(v, u);}cntStart[depth[u]] += cnt_s[u];for (auto id : tId[u]) {++cntLast[pla[id].e - depth[pla[id].t] + Size];}result[u] += (cntStart[depth[u] + vct_w[u]] - tot1) + (cntLast[vct_w[u] - depth[u] + Size] - tot2);for (auto id : LId[u]) {--cntStart[depth[pla[id].s]];--cntLast[pla[id].e - depth[pla[id].t] + Size];}return;
}int main() {ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);LL n, m, u, v;cin >> n >> m;for (LL i = 1; i < n; ++i) {cin >> u >> v;tree[u].emplace_back(v);tree[v].emplace_back(u);}for (LL i = 1; i <= n; ++i)  cin >> vct_w[i];init(1, 0);LL lcaId = 0;for (LL i = 1; i <= m; ++i) {cin >> pla[i].s >> pla[i].t;lcaId = LCA(pla[i].s, pla[i].t);pla[i].e = depth[pla[i].s] + depth[pla[i].t] - depth[lcaId] * 2;++cnt_s[pla[i].s];tId[pla[i].t].emplace_back(i);LId[lcaId].emplace_back(i);if (depth[pla[i].s] == depth[lcaId] + vct_w[lcaId])  --result[lcaId];}dfs(1, 0);for (LL i = 1; i <= n; ++i)  cout << result[i] << ' ';return 0;
}